Similar presentations:
Предмет и задачи начального обучения математике в школе для детей с тяжелыми нарушениями речи
1.
2.
Методика преподавания математики - разделпедагогики, исследующий закономерности обучения
математике на определённом уровне её развития в
соответствии с целями обучения, поставленными
обществом.
Предметом специальной методики математики
является обучение математике в школе V вида.
Задачами курса обучения математике в специальной
(коррекционной) школе V вида являются –
формирование у учащихся прочных навыков счета,
решение текстовых задач, развитие мышления, памяти,
внимания, творческого воображения,
наблюдательности, формирование умения кратко,
точно и ясно излагать свои мысли.
3.
В процессе обучения обеспечивается формированиенавыков фонетически правильной разговорной речи,
расширение лексического запаса, обучение
грамматически правильному оформлению
высказывания, чтению и письму.
Однако главной общеобразовательной задачей
обучения математике является овладение учащимися
системой доступных математических знаний, умений и
навыков, необходимых в повседневной жизни и в
будущей профессии.
4.
ПедагогикаПсихология
Математика
Логика
Логопедия
Методики
обучения
5.
Роль процесса обучения математикев развитии познавательной деятельности
школьников с тяжелыми нарушениями речи
Тяжелые речевые дефекты отрицательно сказываются на
развитии познавательной деятельности и поведении детей:
нарушения речи затрудняют
окружающими людьми,
общение
ребенка
вызывают отрицательные переживания,
осложняют процесс обучения и жизнь в обществе.
с
6.
способность к формализованному восприятиюматематического материала (схватыванию формальной
структуры задачи),
способность к быстрому и широкому обобщению
математических объектов, отношений, действий,
способность мыслить свернутыми структурами
(свертывание процесса математического рассуждения),
гибкость мыслительных процессов,
способность к быстрой перестройке направленности
мыслительного процесса,
математическая память (обобщенная память на
математические отношения, методы решения задач,
принципы подхода к ним).
7.
Математика обладает большим воспитательнымпотенциалом, процессе обучения математике:
формируется
критичность
мышления,
способность к размышлениям и творчеству,
происходит
развитие
математического мышления,
элементарного
формирование и коррекция форм мышления,
как сравнение, анализ, синтез,
развиваются
конкретизации,
способности
к
обобщению
и
создаются условия для коррекции памяти,
внимания и других психических функций.
8.
Уроки математики направлены на преодоление основногоречевого дефекта и нарушений психического развития
учащихся:
расширение, обогащение и активизация словарного
запаса за счёт введения в речь математической
терминологии;
развитие грамматического строя речи за счёт включения
математических терминов в различные грамматические
конструкции (словосочетание и предложение);
развитие навыка смыслового чтения и навыков работы с
информацией, представленной разными способами (чтение
текста задачи, формулировка правила, составление таблиц и
алгоритмов);
9.
развитие связной устной и письменной речи(составление связного учебного высказывания с опорой
на алгоритм, оречевление собственных действий,
использование в связной речи новой математической
терминологии);
формирование коммуникативной функции речи за
счёт специально организованных ситуаций общения на
уроке математики (диалог, работа в парах, в группах и
пр.);
развитие
высших
психических
формирование абстрактного мышления,
обобщать, классифицировать;
функций,
обучение
профилактика дискалькулии;
автоматизация звукопроизношения в процессе
построения речевого высказывания учащихся.
10.
Математика являетсяодним из самых трудных
предметов для этой категории
учащихся.
С одной стороны, это
объясняется абстрактностью
математических понятий, с
другой стороны,
особенностями усвоения
математических знаний
учащимися.
11.
Особенности восприятияУзость, не целенаправленность и слабая активность
восприятия создают определенные трудности в
понимании задачи, математического задания. Учащиеся
воспринимают задачу не полностью, а фрагментарно, а
несовершенство анализа и синтеза не позволяет эти
части связать в единое целое, установить между ними
связи и зависимости и, исходя из этого, выбрать
правильный путь решения.
Слабая активность восприятия приводит к тому, что
учащиеся не узнают знакомые геометрические фигуры,
если они даются в непривычном положении или их
нужно выделить в предметах, найти в окружающей
обстановке.
Они не могут найти в задаче числовые данные, если
они записаны не цифрами, а словами, выделить
вопрос, если он стоит не в конце, а в начале или в
середине задачи, и т.д.
12.
Особенности письменной речиТрудности при обучении математике вызываются
также
несовершенством
зрительных
восприятий
(зрительного анализа и синтеза) и моторики учащихся.
Это проявляется в обучении письму вообще и цифр в
частности.
Затрудненность письма у некоторых учащихся
усугубляется тремором (дрожанием) рук, параличами.
Нарушение координации движений у отдельных
учащихся нередко служит причиной очень сильного
нажима при письме, который приводит к поломке
карандаша и прорыву бумаги.
Несовершенство зрительных восприятий, трудности
пространственной ориентировки приводят к тому, что
учащиеся не видят строки и не понимают ее значения.
13.
Другойпричиной
слабой
дифференцированности
математических знаний является
отрыв
математической
терминологии
от
конкретных
представлений, реальных образов,
объектов,
в
непонимании
конкретной
ситуации
задачи,
математических зависимостей и
отношений между данными, а также
между данными и искомыми.
Например,
учащиеся не
представляют
себе реально
таких единиц
измерения, как
километр и
килограмм, а
некоторое
сходство в их
звучании приводит
к их уподоблению.
14.
Особенности мыслительной деятельностиСлабость обобщений проявляется в механическом
заучивании правил, без понимания их смысла, без
осознания того, когда их можно применить.
Низкий
уровень
мыслительной
деятельности
школьников с нарушением речи затрудняет переход от
практических действий к умственным. Недостатки
гибкости мышления проявляются в подборе примеров к
правилам, при составлении задач: учащиеся нередко
составляют
задачи
с
одинаковой
фабулой,
повторяющимися глаголами, числовыми данными,
вопросами и т.д.
15.
Особенности словарного запасаБедность словаря, непонимание значения слов и
выражений создают значительные трудности в
обучении математике, особенно в обучении решению
задач. Нередко учащиеся не решают задачу потому, что
не понимают значения слов, выражений, предметной
ситуации задачи, а также той математической
«нагрузки», которую несут такие слова, как другой,
второй, оба, каждый, столько же.
Бедность словаря проявляется и при составлении
задач: учащиеся оперируют словами-штампами, не
могут избежать слов-штампов в формулировке
вопросов, заменяя специфические слова в вопросах
общим словом сколько. Некоторые, импульсивно, не
обдумывая условия, говорят: «Я не знаю, как решать
такую задачу. Мы таких не решали!» они отодвигают
тетради и не пытаются решать задачу.
16.
Особенности звукопроизношения играмматического строя речи
Нарушения звукопроизношения влияют на
процесс прочтения задачи, дети читают текст и
одновременно контролируют свое произношение и
в результате не понимают смысл прочитанного.
Недостатки
грамматического
строя
речи
сказываются особенно на понимание предлогов.
Учащиеся не понимают задачи с нагромождением
предлогов, таких как: «яблоки лежали в коробке, 2
достали из коробки …», учащиеся не могут сами
составить задачу даже по образцу.
17.
Дети имеют практические навыки счета, могут выполнитьсравнение численности групп предметов, действия сложения и
вычитания. Однако их знания о множестве, числе и счете
неустойчивы, требуют постоянной зрительной опоры.
Недостаточно обобщенный сенсорный опыт затрудняет
расширение и углубление знаний о зависимостях и отношениях
между величинами.
Словесное сопровождение хода выполнения задания
значительно снижает темп работы. Трудности в речевом
регулировании деятельности препятствуют самостоятельному
исправлению ошибок, формированию самоконтроля. Дети не
могут проконтролировать одновременно речевую и
практическую деятельность.
18.
Несмотря на то, что дети умеют создаватьсериационный ряд по величине, различают длину,
ширину и высоту предмета, им тяжело оперировать
имеющимися знаниями, включать их в более сложную
деятельность. Поскольку для этого необходимо
использовать в речи различные формы имен
прилагательных, что для дошкольников и младших
школьников с нарушениями речи крайне трудно, они не
могут определить величину предмета.
19.
20.
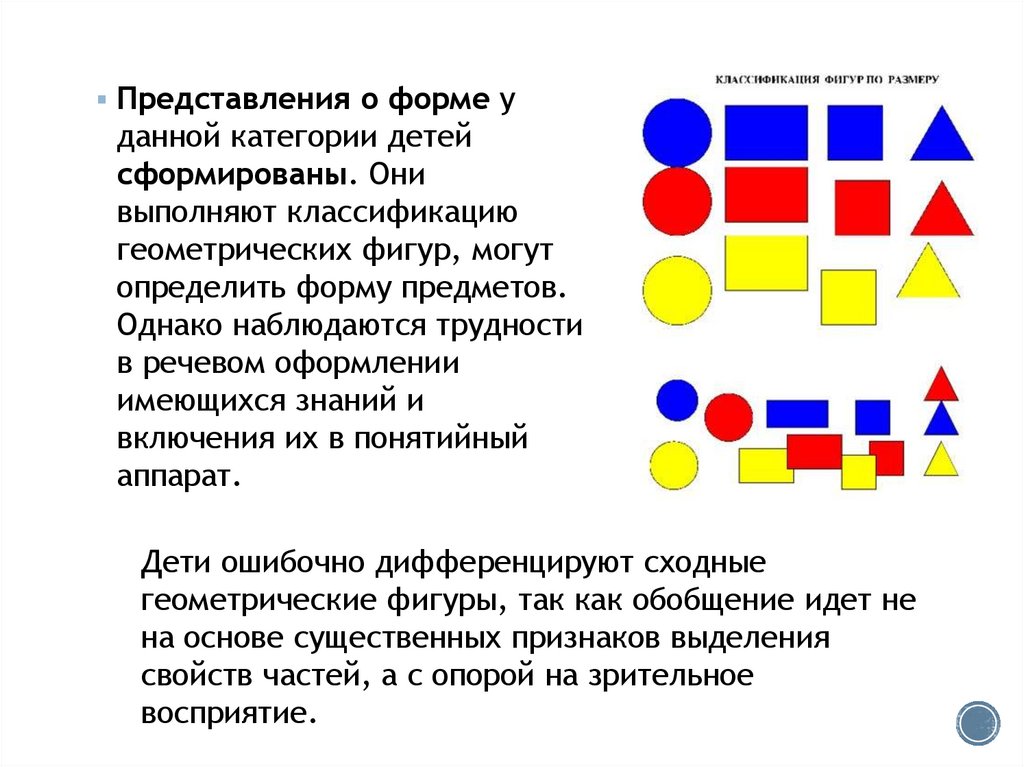
Представления о форме уданной категории детей
сформированы. Они
выполняют классификацию
геометрических фигур, могут
определить форму предметов.
Однако наблюдаются трудности
в речевом оформлении
имеющихся знаний и
включения их в понятийный
аппарат.
Дети ошибочно дифференцируют сходные
геометрические фигуры, так как обобщение идет не
на основе существенных признаков выделения
свойств частей, а с опорой на зрительное
восприятие.
21.
Дети понимают значение основных, наиболее частоупотребляемых
предлогов
и
наречий.
Однако
затруднено активное пользование этих частей речи в
произвольном
высказывании,
что
осложняет
осмысление и оценивание расположения объекта и
отношений между ними.
Характеризуя восприятие времени школьниками,
можно сказать, что в целом они понимают смену
событий, их периодичность, определяют основные
признаки временных интервалов. Несмотря на это,
представление о времени у них бедное, поверхностное,
поскольку не сформировано умение строить длинные
высказывания
о
содержании
деятельности
в
определенный отрезок времени, нет способов оценки
разных
сторон
времени,
необходимых
для
регулирования своей собственной деятельности. Они
не объясняют причинно-следственные временные
связи, не понимают смысла слов, обозначающих
относительные временные отношения (вчера, сегодня,
завтра).
22.
При выполнении знакомых математических заданийдетям
требуется
не
только
организующая
и
направляющая помощь, но и частичный разбор
выполняемых действий, упрощение задания и часто
полный совместный разбор, а также совместное
выполнение всего задания.
Они не умеют пользоваться словесными образцами,
не опираются на них при построении фразы,
затрудняются осуществить перенос на аналогичное
задание.
Большинство детей не могут запомнить инструкцию,
удержать
в
памяти
вербальную
организацию
практического задания. Это осложняет не только
обучение математике, но и формирование навыков
учебной деятельности.





















 mathematics
mathematics








