Similar presentations:
Теорема Гаусса и её применение к расчету электрических полей. Лекция 14
1.
ЭЛЕКТРОСТАТИКАЛекция 14.
Тема: Теорема Гаусса и её применение к расчету
электрических полей.
Учебник:
Трофимова Т.И. Курс физики : учеб. пособ. для вузов / Т. И.
Трофимова. - М.: Академия, 2007.- с. 152-155.
к.ф.-м.н.
Курочкин А.Р.
2.
Поток вектора напряжённости электрического поляИсходные посылки:
S – поверхность, находящаяся
в электрическом поле;
dS – элементарная (бесконечно
малая) площадка на этой
поверхности (обозначена синим
цветом);
единичный
вектор
n –
нормали к площадке dS n 1 .
dS
E – напряжённость электрического поля в той точке, где
находится площадка dS;
α – угол между векторами E и n .
2
3.
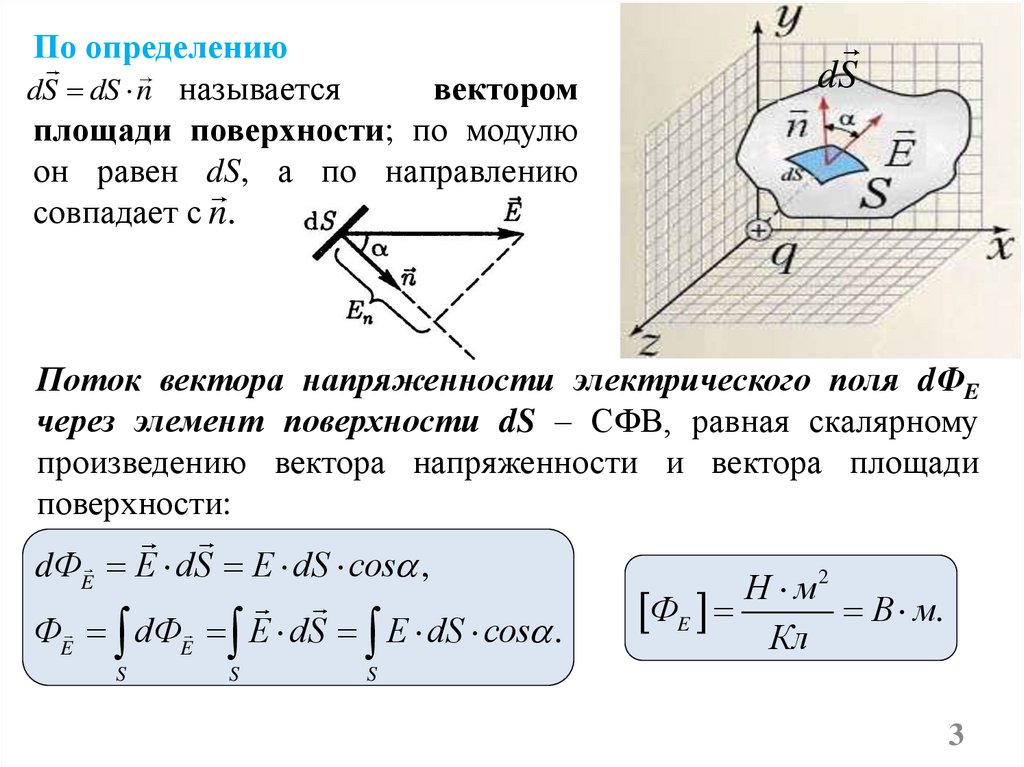
По определениювектором
dS dS n называется
площади поверхности; по модулю
он равен dS, а по направлению
совпадает с n.
dS
Поток вектора напряженности электрического поля dФE
через элемент поверхности dS – СФВ, равная скалярному
произведению вектора напряженности и вектора площади
поверхности:
dФE E dS E dS сos ,
ФE dФE E dS E dS сos .
S
S
Н м2
В м.
ФE
Кл
S
3
4.
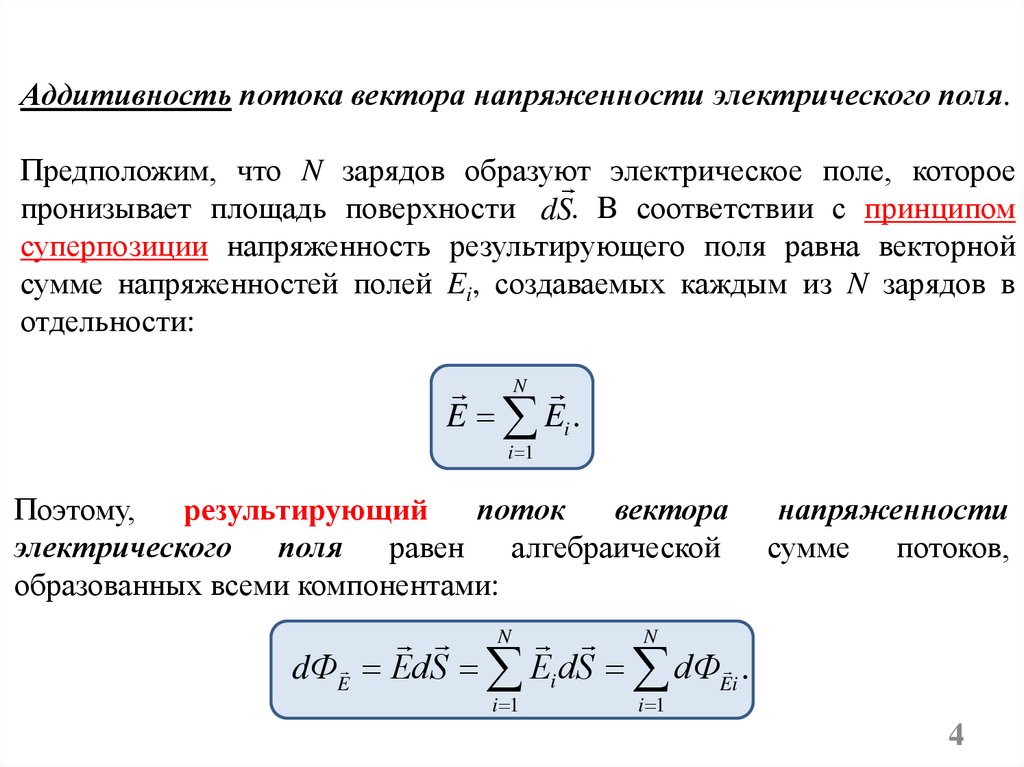
Аддитивность потока вектора напряженности электрического поля.Предположим, что N зарядов образуют электрическое поле, которое
пронизывает площадь поверхности dS. В соответствии с принципом
суперпозиции напряженность результирующего поля равна векторной
сумме напряженностей полей Ei, создаваемых каждым из N зарядов в
отдельности:
N
E Ei .
i 1
Поэтому,
результирующий
поток
вектора
электрического поля равен алгебраической
образованных всеми компонентами:
N
N
i 1
i 1
напряженности
сумме потоков,
dФE EdS Ei dS dФEi .
4
5.
В каких случаях легко получитьвыражение для потока ФE вектора E ?
аналитическое
1) Если вектор E направлен по касательной к поверхности, то в
этом случае E n , сos 0 ФE 0;
E
dS
n
2) Если вектор
E во всех точках поверхности имеет
одинаковую величину (E=const) и направлен перпендикулярно
поверхности E n, 0 сos 1 , в этом случае ФE=E∙S.
dS
n
E
3) Если однородное электрическое поле пронизывает плоскую
поверхность S (α=const), тогда ФE=E∙S∙cosα.
E
dS
n
5
6.
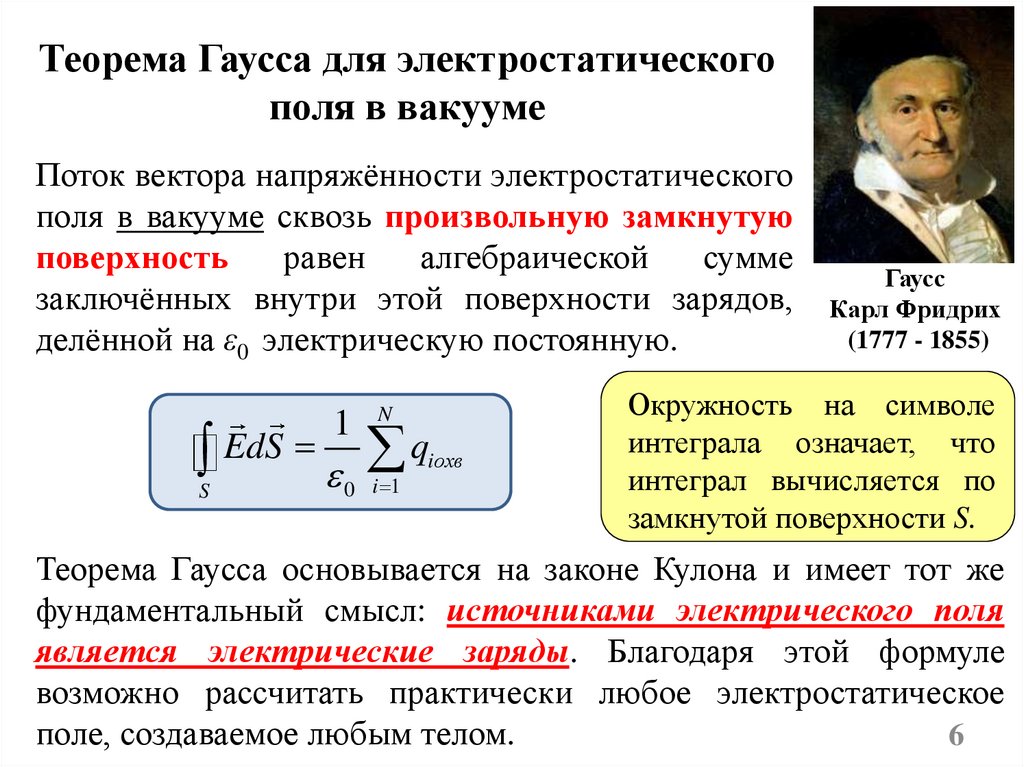
Теорема Гаусса для электростатическогополя в вакууме
Поток вектора напряжённости электростатического
поля в вакууме сквозь произвольную замкнутую
поверхность
равен
алгебраической
сумме
заключённых внутри этой поверхности зарядов,
делённой на ε0 электрическую постоянную.
1
N
EdS q
S
0 i 1
iохв
Гаусс
Карл Фридрих
(1777 - 1855)
Окружность на символе
интеграла означает, что
интеграл вычисляется по
замкнутой поверхности S.
Теорема Гаусса основывается на законе Кулона и имеет тот же
фундаментальный смысл: источниками электрического поля
является электрические заряды. Благодаря этой формуле
возможно рассчитать практически любое электростатическое
поле, создаваемое любым телом.
6
7.
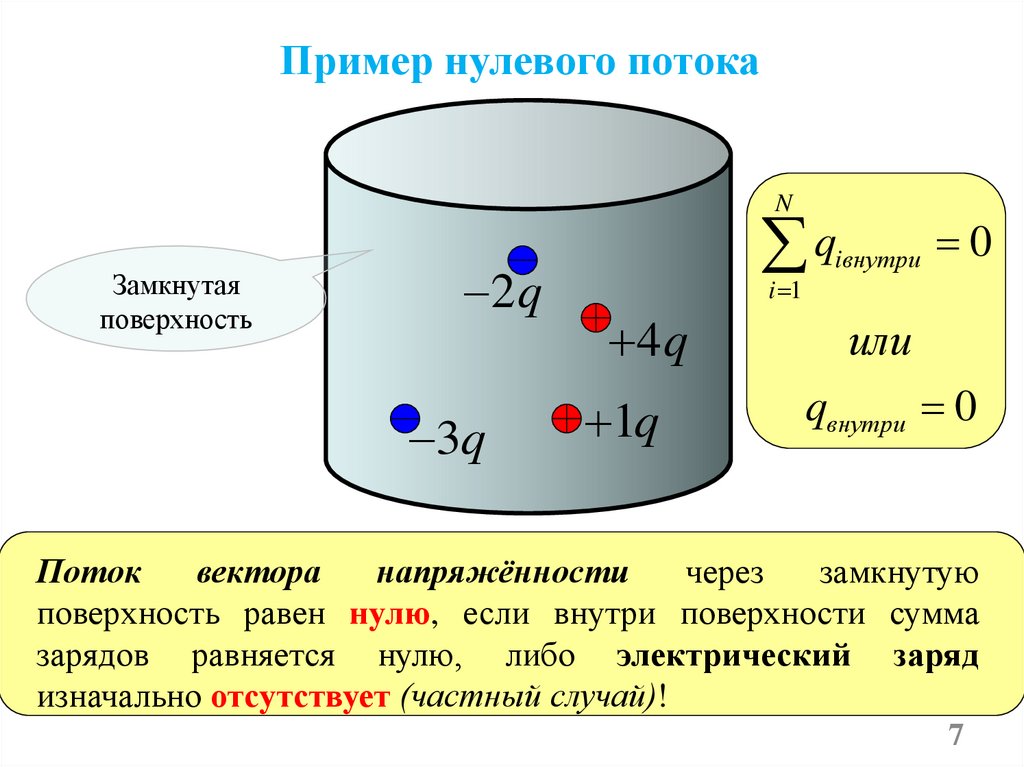
Пример нулевого потокаN
Замкнутая
поверхность
2q
3q
q
i 1
4q
1q
iвнутри
0
или
qвнутри 0
Поток
вектора
напряжённости
через
замкнутую
поверхность равен нулю, если внутри поверхности сумма
зарядов равняется нулю, либо электрический заряд
изначально отсутствует (частный случай)!
7
8.
Алгоритм расчёта электрического поляс использованием теоремы Гаусса.
Постановка задачи: рассчитаем напряжённость электрического
поля, созданного симметричным заряженным телом с заданной
плотностью заряда в произвольной точке A.
Алгоритм решения
Формулировка
Пояснение
1. Проанализируем а) как направлены линии напряжённости?
характер
б) на каких поверхностях модуль вектора E имеет
симметрии поля: постоянное значение?
2. Выбрать
замкнутую
гауссову
поверхность так,
чтобы:
а) она проходила через точку A;
б) было легко получить аналитическое выражение
для потока вектора E ;
в) было легко рассчитать заряд, охваченный этой
поверхностью.
8
9.
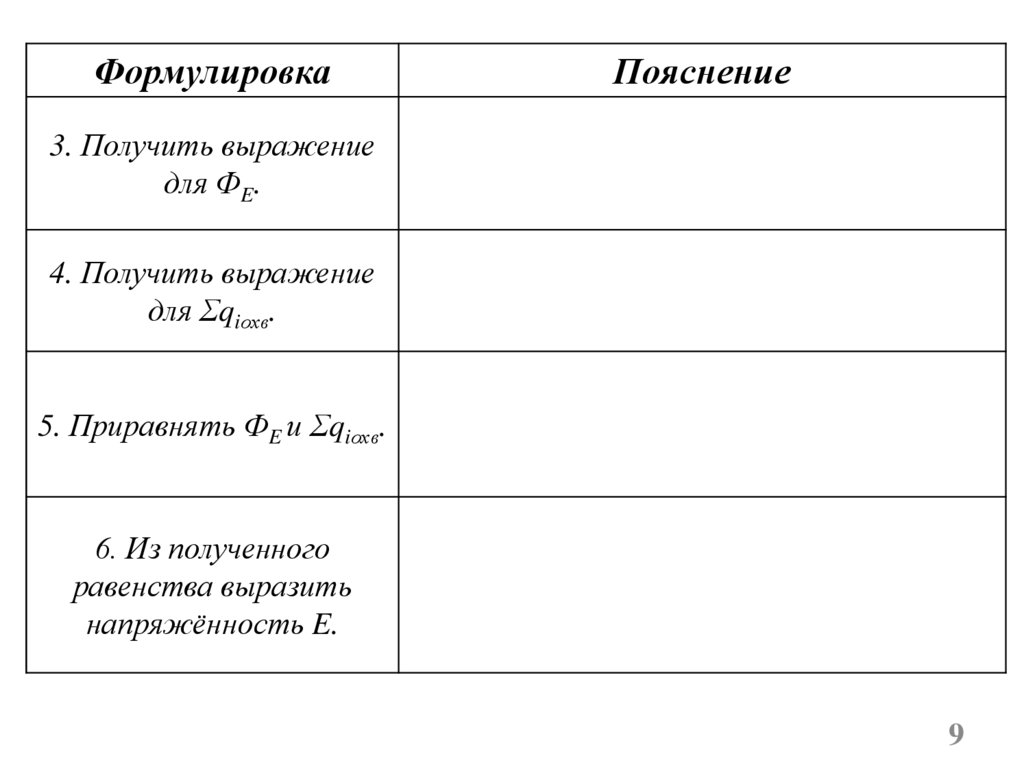
ФормулировкаПояснение
3. Получить выражение
для ФE.
4. Получить выражение
для Σqiохв.
5. Приравнять ФE и Σqiохв.
6. Из полученного
равенства выразить
напряжённость E.
9
10.
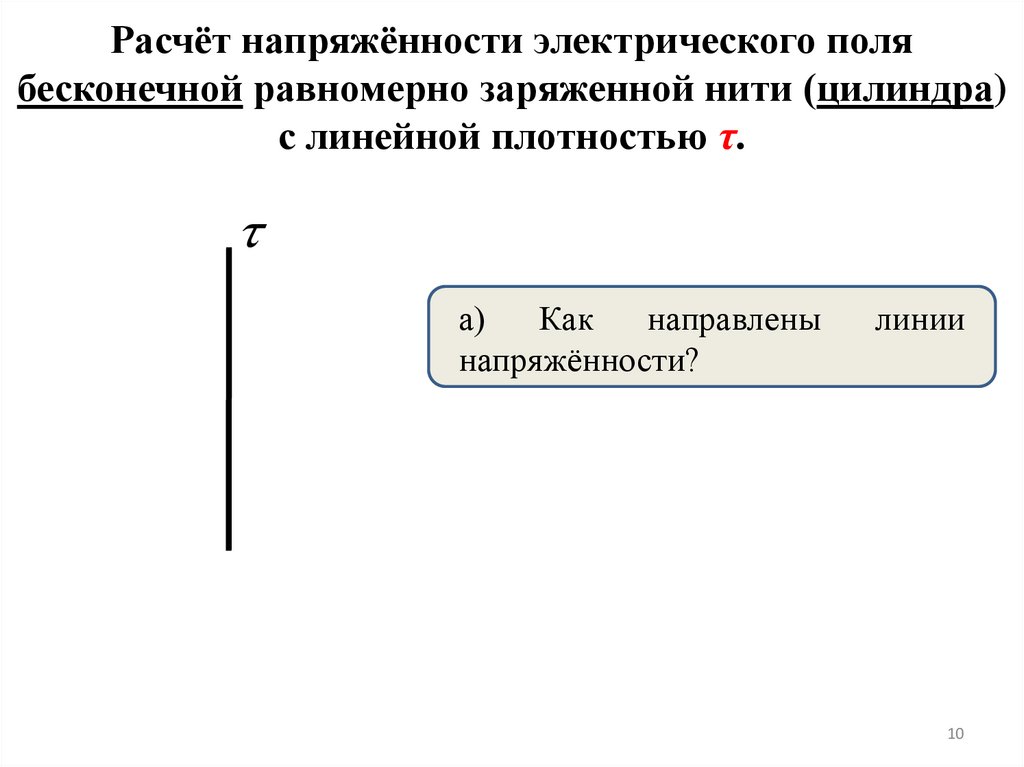
Расчёт напряжённости электрического полябесконечной равномерно заряженной нити (цилиндра)
с линейной плотностью τ.
а)
Как
направлены
напряжённости?
линии
10
11.
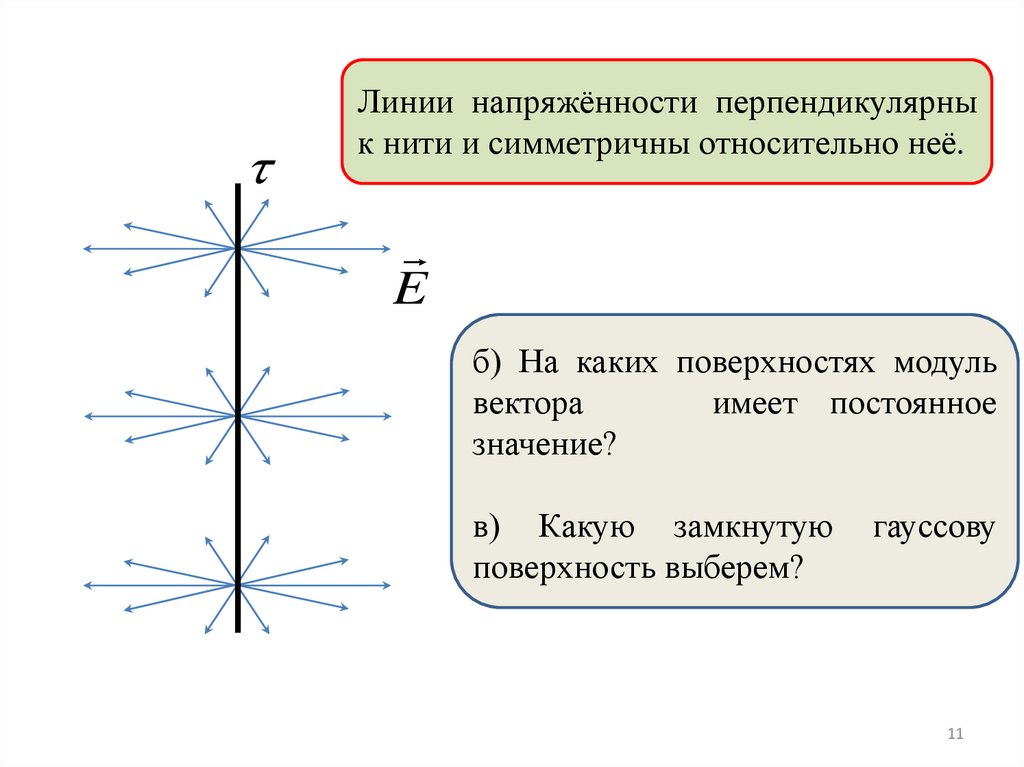
Линии напряжённости перпендикулярнык нити и симметричны относительно неё.
E
б) На каких поверхностях модуль
вектора
имеет постоянное
значение?
в) Какую замкнутую
поверхность выберем?
гауссову
11
12.
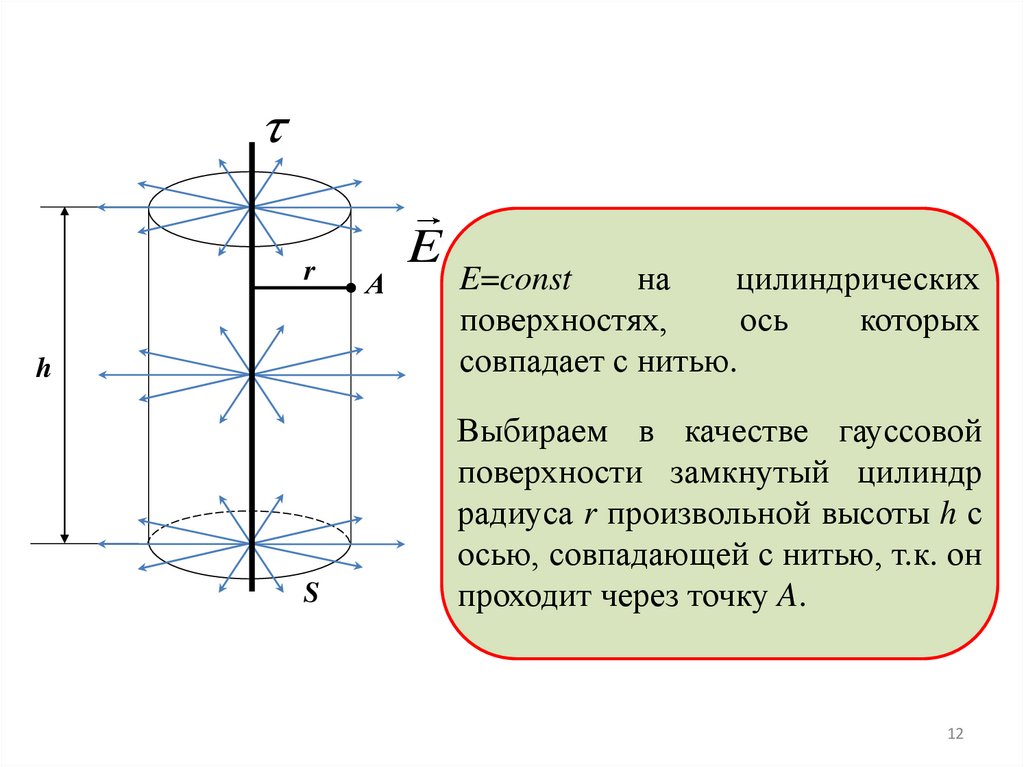
rh
S
А
E
E=const
на
цилиндрических
поверхностях,
ось
которых
совпадает с нитью.
Выбираем в качестве гауссовой
поверхности замкнутый цилиндр
радиуса r произвольной высоты h с
осью, совпадающей с нитью, т.к. он
проходит через точку A.
12
13.
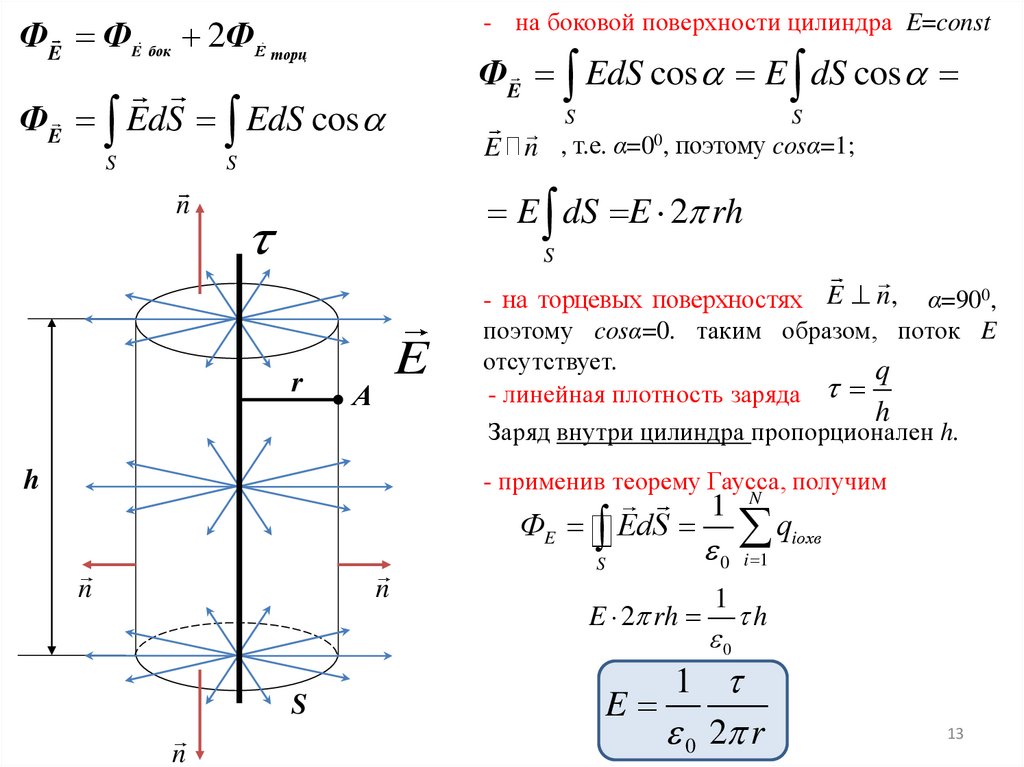
- на боковой поверхности цилиндра E=constФE ФE бок 2ФE торц
ФE EdS cos E dS cos
ФE EdS EdS cos
S
S
E n , т.е. α=00, поэтому cosα=1;
S
n
S
E dS E 2 rh
S
r
E
А
- на торцевых поверхностях E n , α=900,
поэтому cosα=0. таким образом, поток E
отсутствует.
q
- линейная плотность заряда
h
Заряд внутри цилиндра пропорционален h.
- применив теорему Гаусса, получим
h
ФE
1
EdS q
S
n
n
S
n
N
E 2 rh
0 i 1
1
0
iохв
h
1
E
0 2 r
13
14.
Формулы для расчета некоторыхэлектростатических полей в вакууме
n
1. Поле точечного заряда
• Поле точечного заряда обладает центральной
симметрией;
• Выберем в качестве произвольной замкнутой
поверхности сферу радиуса r;
• Для всех точек этой сферы E(r)=const;
• Запишем теорему Гаусса
ФE
EdS
S
ФE
S
EdS
S
EndS
q
n
q
S
E
n
0
EdS cos
r
E n 0
S
EdS E dS E 4 r 2
S
1 q
E
4 0 r 2
14
15.
Формулы для расчета некоторыхэлектростатических полей в вакууме
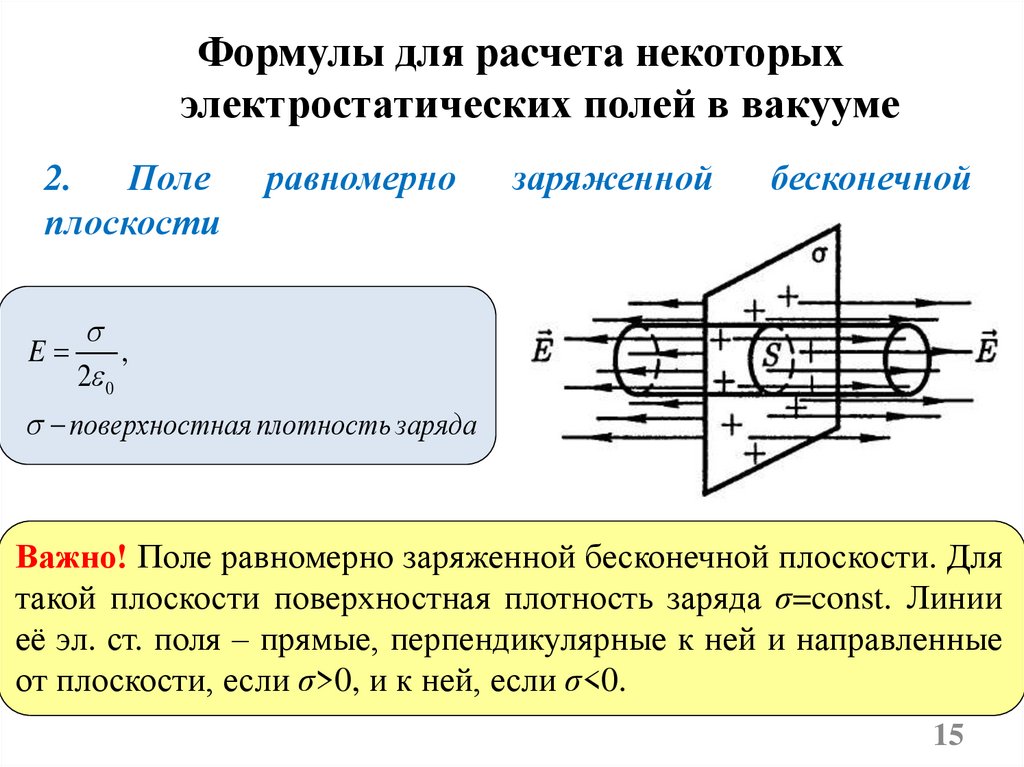
2. Поле
плоскости
равномерно
заряженной
бесконечной
,
2 0
поверхностная плотность заряда
E
Важно! Поле равномерно заряженной бесконечной плоскости. Для
такой плоскости поверхностная плотность заряда σ=const. Линии
её эл. ст. поля – прямые, перпендикулярные к ней и направленные
от плоскости, если σ>0, и к ней, если σ<0.
15
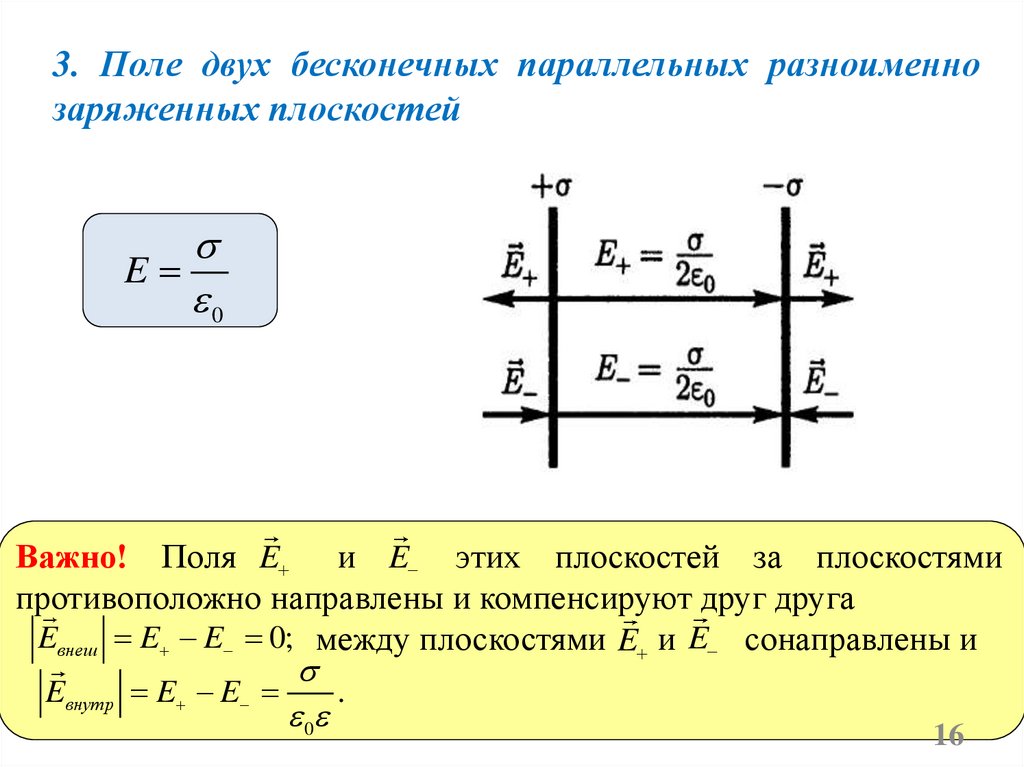
16.
3. Поле двух бесконечных параллельных разноименнозаряженных плоскостей
E
0
Важно! Поля E и E этих плоскостей за плоскостями
противоположно направлены и компенсируют друг друга
Eвнеш E E 0; между плоскостями E и E сонаправлены и
Eвнутр E E
.
0
16
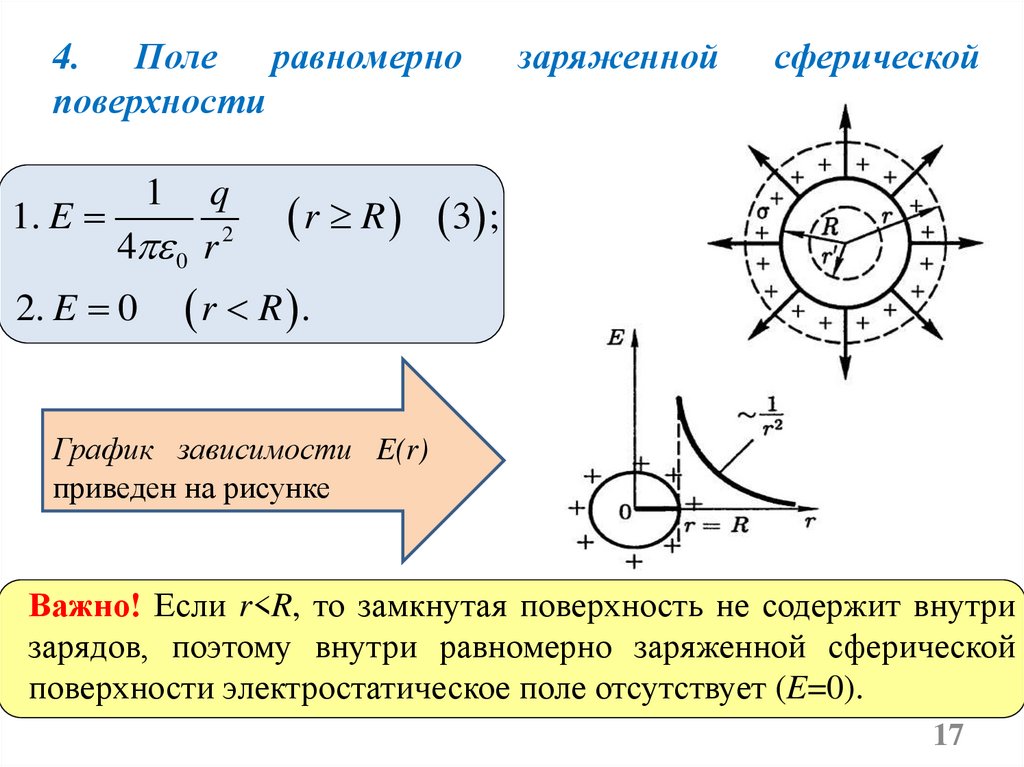
17.
4. Поле равномерноповерхности
1
q
1. E
4 0 r 2
2. E 0
заряженной
сферической
r R 3 ;
r R .
График зависимости E(r)
приведен на рисунке
Важно! Если r<R, то замкнутая поверхность не содержит внутри
зарядов, поэтому внутри равномерно заряженной сферической
поверхности электростатическое поле отсутствует (E=0).
17
18.
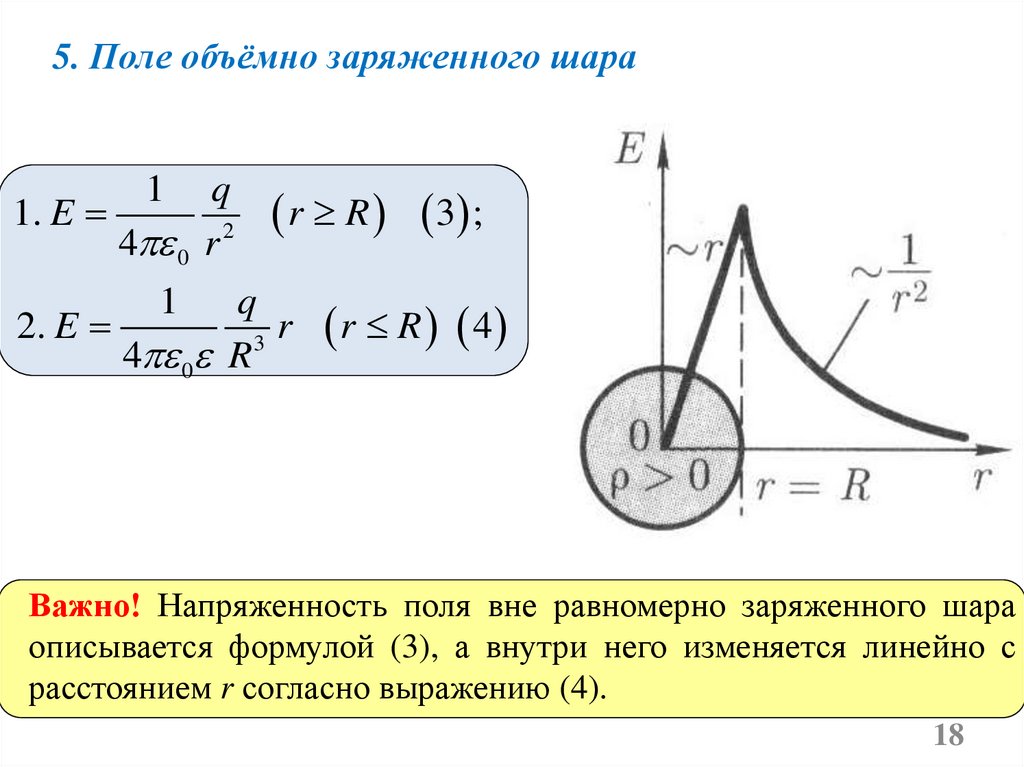
5. Поле объёмно заряженного шара1
q
1. E
4 0 r 2
1
r R 3 ;
q
2. E
r
3
4 0 R
r R 4
Важно! Напряженность поля вне равномерно заряженного шара
описывается формулой (3), а внутри него изменяется линейно с
расстоянием r согласно выражению (4).
18
19.
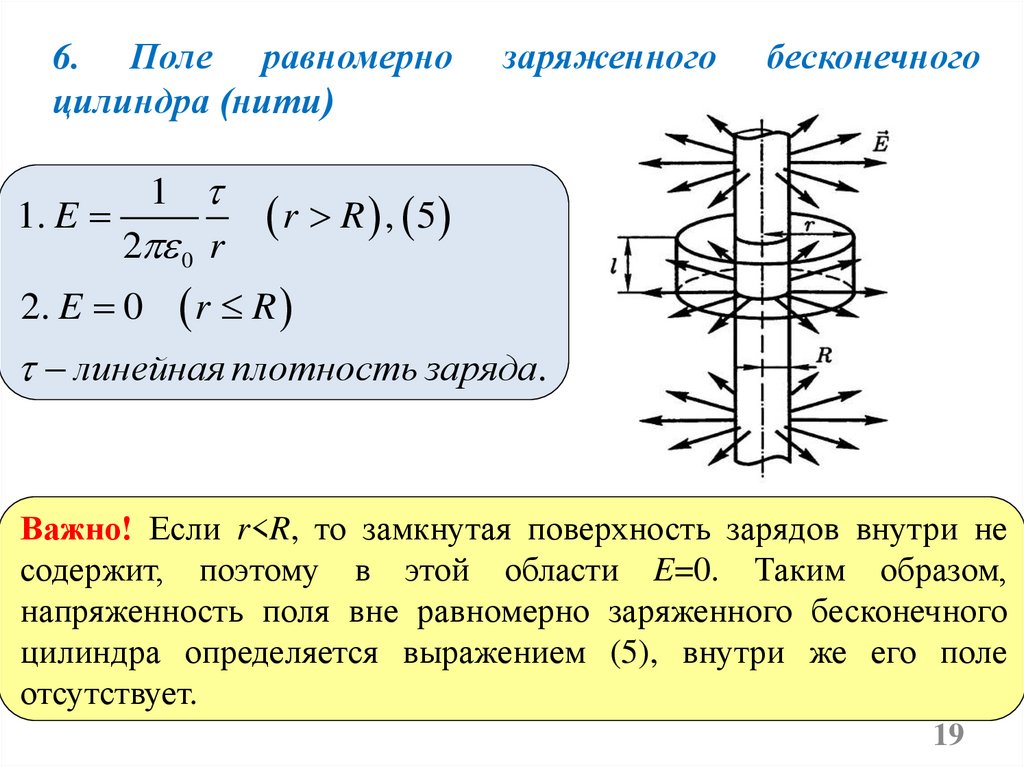
6. Поле равномерноцилиндра (нити)
1
1. E
2 0 r
2. E 0
заряженного
бесконечного
r R , 5
r R
линейная плотность заряда.
Важно! Если r<R, то замкнутая поверхность зарядов внутри не
содержит, поэтому в этой области E=0. Таким образом,
напряженность поля вне равномерно заряженного бесконечного
цилиндра определяется выражением (5), внутри же его поле
отсутствует.
19
20.
Пример задачи, решаемой с помощью теоремы ГауссаУсловие задачи. Дана система точечных
зарядов в вакууме и замкнутые
поверхности S1, S2 и S3, причем
поверхность S3 охватывает поверхность
S2, которая в свою очередь охватывает
поверхность S1.
Решение. Согласно теореме Гаусса поток
Вопрос. Поток
напряжённости электростатического поля в
напряженности
вакууме
сквозь
произвольную
замкнутую
электростатического поверхность равен отношению алгебраической
поля отличен от
суммы электрических зарядов, охватываемых
нуля сквозь…
этой
поверхностью,
иN
электрической
1
-поверхность S1
постоянной ε0, Nт.е. ФE EdS qiохв . Из условия
0 i 1
S
-поверхность S3
q
0
видим, что i
только для поверхности S1,
i
1
-поверхность S2
поэтому напряженности электростатического
-поверхность S4
поля отличен от нуля сквозь поверхность S1.
20






 physics
physics








