Теория и применение радиолокационных сигналов. Лекция 05

1.

Теория и применение
радиолокационных сигналов
Лекция 05
Сигнал с фазо-кодовой манипуляцией

2.

Фазокодоманимулированный сигнал
Фазовая (фазокодовая) манипуляция (ФКМ) позволяет расширить
амплитудно-частотного
спектр
сигнала,
что
улучшает
разрешающую способность по дальности.
Сигнал
представляет
собой
совокупность
сомкнутых
радиоимпульсов (дискрет) с общей частотой несущей f0 и
одинаковыми длительностями τд, начальная фаза в каждом
дискрете выбирается из совокупности возможных сдвигов фаз φq
(q = 0,1,…,p-1) относительно опорного колебания.
Структуру сигнала обычно записывают в виде цифровой
последовательности, элементы которой принадлежат системе
счисления размерности p.
Начальные фазы обычно равномерно распределены на интервале
[0; 2π], но встречается и неравномерное распределение. Для
равномерного распределения начальные фазы имеют вид:
q 2 q p , где q 0, 1, ..., p 1

3.

Применяемые коды для ФКМ сигналов
Наиболее распространенны в локации являются ФКМ,
использующие двоичный код (p = 2):
• код Баркера;
• М-последовательность;
• коды Голда.
В системах связи наиболее распространены:
• коды Уолша;
• коды Голда;
• коды Касами.
Выражение для комплексной огибающей ФКМ импульса можно
представить в виде:
U( t )
N Д 1
U
k 0
Д
( t Д k )
exp i n , при 0 t Д
UД(t )
0, при других t.

4.

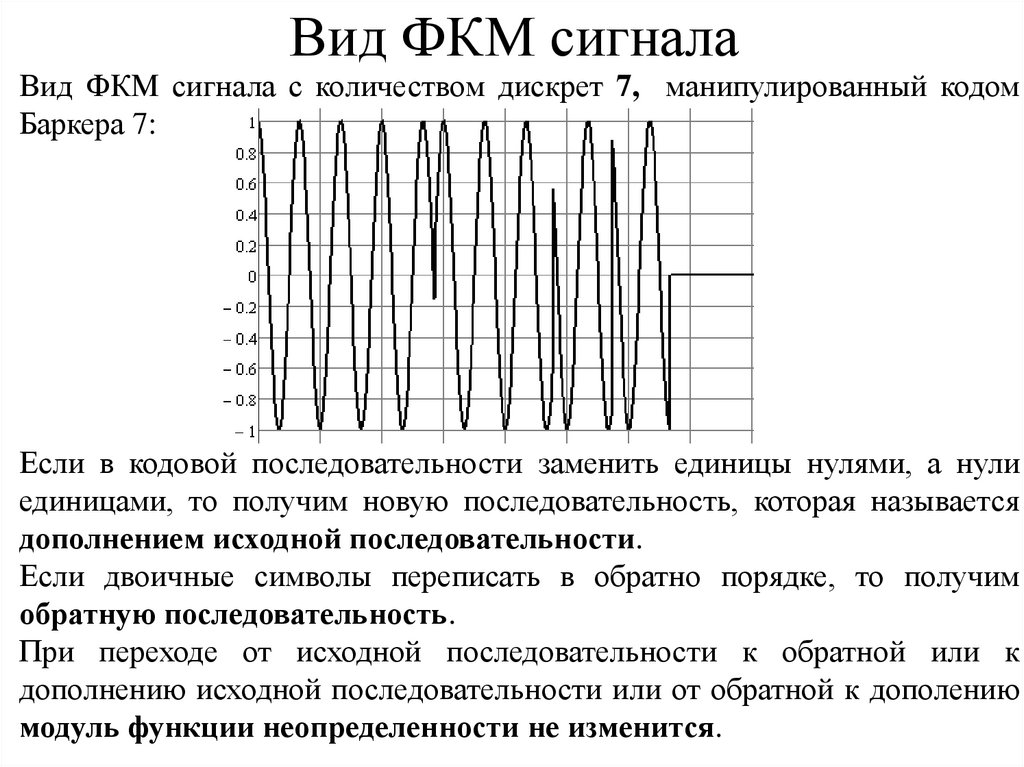
Вид ФКМ сигнала
Вид ФКМ сигнала с количеством дискрет 7, манипулированный кодом
Баркера 7:
Если в кодовой последовательности заменить единицы нулями, а нули
единицами, то получим новую последовательность, которая называется
дополнением исходной последовательности.
Если двоичные символы переписать в обратно порядке, то получим
обратную последовательность.
При переходе от исходной последовательности к обратной или к
дополнению исходной последовательности или от обратной к дополению
модуль функции неопределенности не изменится.

5.

Постулаты Голомба
1. В псевдослучайной последовательности количество нулей и
единиц должно отличаться не более чем на 1.
2. В каждом периоде последовательности половина серий
(последовательных одинаковых символов) должна иметь длину
один, четверть серий - должна иметь длину два, одна восьмая
должна иметь длину три и т.д., для каждой из этих длин должно
быть одинаковое количество серий из "1" и "0".
3. Автокорреляционная
функция
псевдослучайной
последовательности должна иметь при рассогласовании на целое
число дискретов не более двух ненулевых значений (единица и
уровень бокового лепестка).
Выполнение этих постулатов обычно не обеспечивается,
большинство кодов не могут удовлетворить третьему постулату,
соответственно
большинство
кодов
–
являются
квазипсевдослучайной последовательностью, однако приставку
«квази-» часто опускают.

6.

Код Баркера
Табличный код, эвристический, постулатам Голомба не
подчиняется, уровень боковых лепестков тела ρ(τ, F) в сечении
F = 0 при двоичной манипуляции с начальными фазами 0; π
составляет 1/nд, где nд – количество дискрет в сигнале.
В настоящее время подобраны такие коды для nд ≤13. Начальная
фаза 0 описывается кодом 0, начальная фаза π описывается кодом 1.
nд
3
4
5
7
11
13
Код Баркера
0, 0, 1
0, 0, 1, 0
0, 0, 0, 1, 0
0, 0, 0, 1, 1, 0, 1
0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1
0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1,0

7.

М-последовательность
Псевдослучайный код, 3 постулату при использовании в пределах
периода не обеспечивает, однако обеспечивает выполнение при
непрерывном излучении в качестве периодического кода.
Период повторения 2m-1, определяется длиной задающего
полинома m.
Существует два рекуррентных метода синтеза кода:
M 1
u i mod m k u i k 1 , 2 , i>M,
k 0
u k mk , k M
M 1
u i mod u i n 1 , 2 , i>M,
n 0
В первом методе начальные значения последовательности могут
быть любыми но не все одинаковые.
Задающий полином (в обоих методах) должен иметь ненулевой
член при старшей степени и не иметь внутренней периодичности

8.

Код Голда
Псевдослучайный код, 3 постулат не обеспечивает, так как имеет не
менее 3х ненулевых значения в ВКФ и АКФ, применяется в
основном
для
синтеза
групп
кодов
для
создания
квазиортогональных созвездий сигналов.
Период повторения 2m-1, определяется длиной задающего
полинома m, количество синтезируемых кодов 2m+1.
Для синтеза кода Голда требуется:
• две
М-последовательности
с
различными
задающими
полиномами;
• выбрать взаимное смещение между последовательностями, в
пределах одного периода.
Gi,sm mod M1i M2i sm ,
i Z, 0 i 2m 2; sm Z, 0 sm 2m
Полученный код Голда имеет тот же период повторения что и
родительские последовательности.

9.

Код Уолша
В основном используется за счет прекрасной взаимной
корреляционной функции.
Основное достоинство – различие между кодами в группе
составляет половину длины кода.
Синтез кода Уолша рекурентный, на основе матрицы Адамара:
A 2i
A 2i 1
A 2i 1
A 2i 1
A 2i 1
;
1
W1 1 ; W2
1
1
1 1
; W4
1
1
1
1 1
1
1
1
1 1
1
1 1 1
1
В основном используется как расширяющий код, то есть для
разделения абонентов, либо для обеспечения высокостабильной
связи, так как размер группы невелик относительно передаваемого
объема информации.

10.

Код Касами
Применяется как альтернатива кодам Голда, так как позволяет
изменять размер кода практически не нарушая постулаты Голомба.
Для синтеза используется 2 М-последовательности с разным
периодом повторения:
K i mod M1i sm1 M2i sm2 ,
длина задающего полинома для M1 N;
длина задающего полинома для M2 N / 2;
период повторения К 2 N 1.
При синтезе начальные полиномы для М-последовательностей
выбираются таким образом, чтобы последовательности были не
коррелированы.
Синтез в значительной мере эвристическая задача, выбранные
смещения последовательностей влияют на свойства кода Касами.
Взаимная корреляционная функция требует смещения между
кодами созвездия не менее чем на N.

11.

ФН одиночного ФКМ импульса
В общем случае ФН ФКМ сигнала имеет вид:
M 1
j F ( )
j 2 F n д
д
sin F д 1 k n k n s e
e
д n 0
j F
e
0 n s M 1
( , F)
M F д
M 1
j 2 F (n 1) д
sin
F
k
k
e
д
n n 1 s
д
0 n n1 0s n 1
д
' – n д , M floor
д

12.

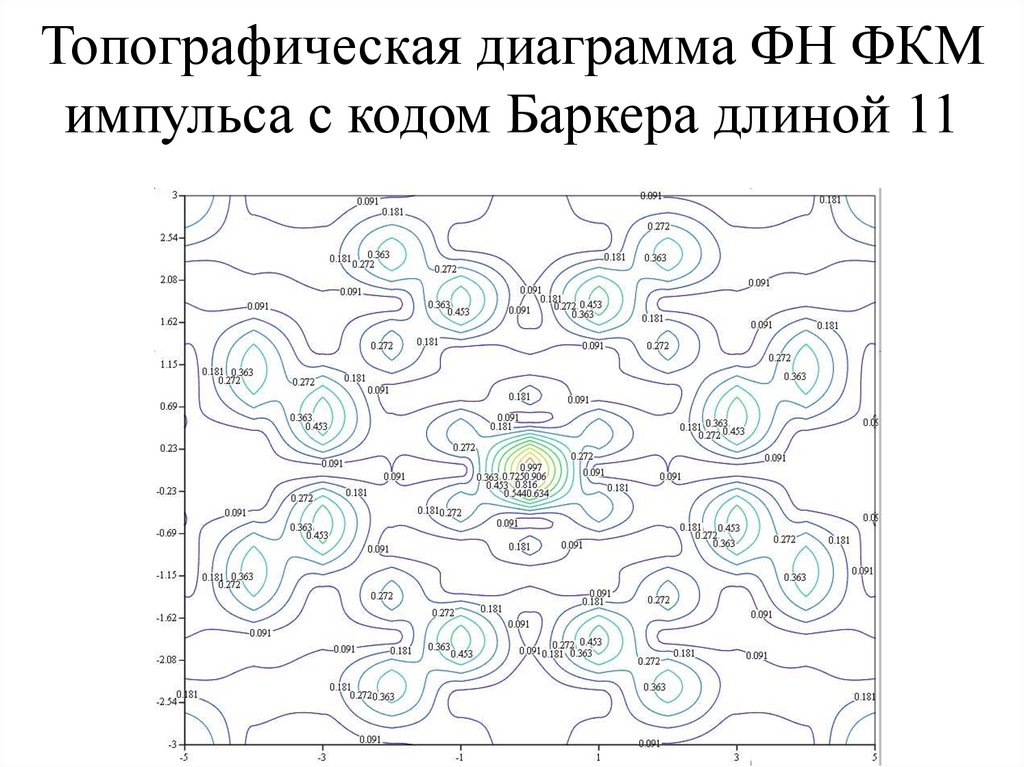
Топографическая диаграмма ФН ФКМ
импульса с кодом Баркера длиной 11

13.

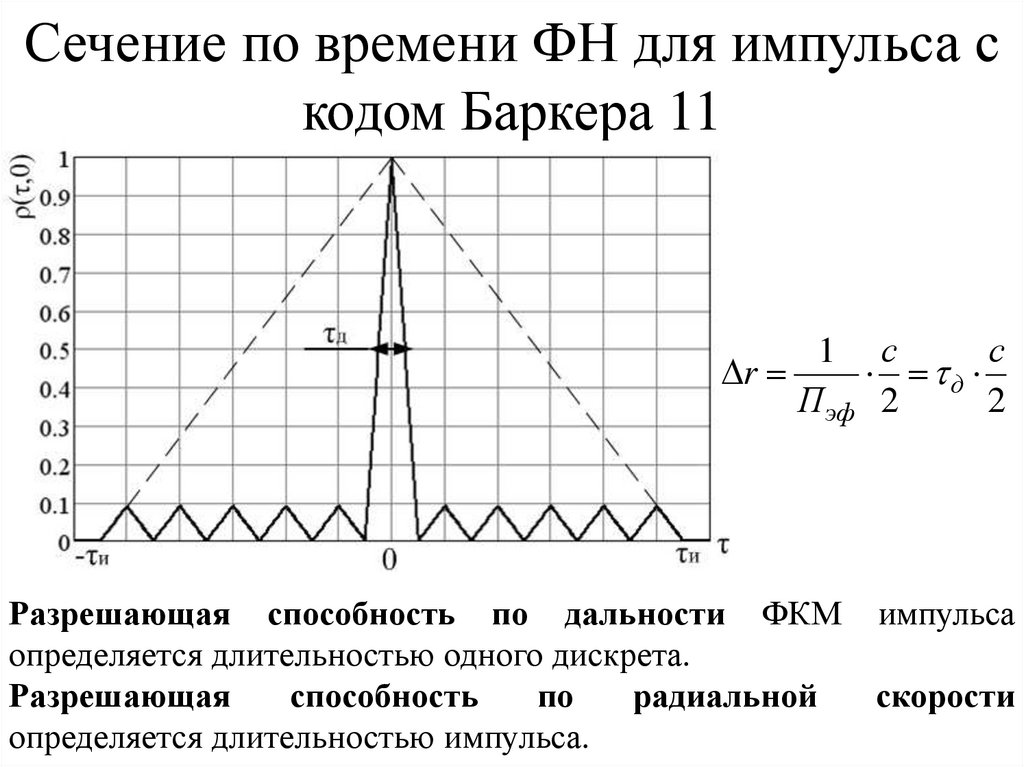
Сечение по времени ФН для импульса с
кодом Баркера 11
1 с
с
r
д
Пэф 2
2
Разрешающая способность по дальности ФКМ импульса
определяется длительностью одного дискрета.
Разрешающая
способность
по
радиальной
скорости
определяется длительностью импульса.

14.

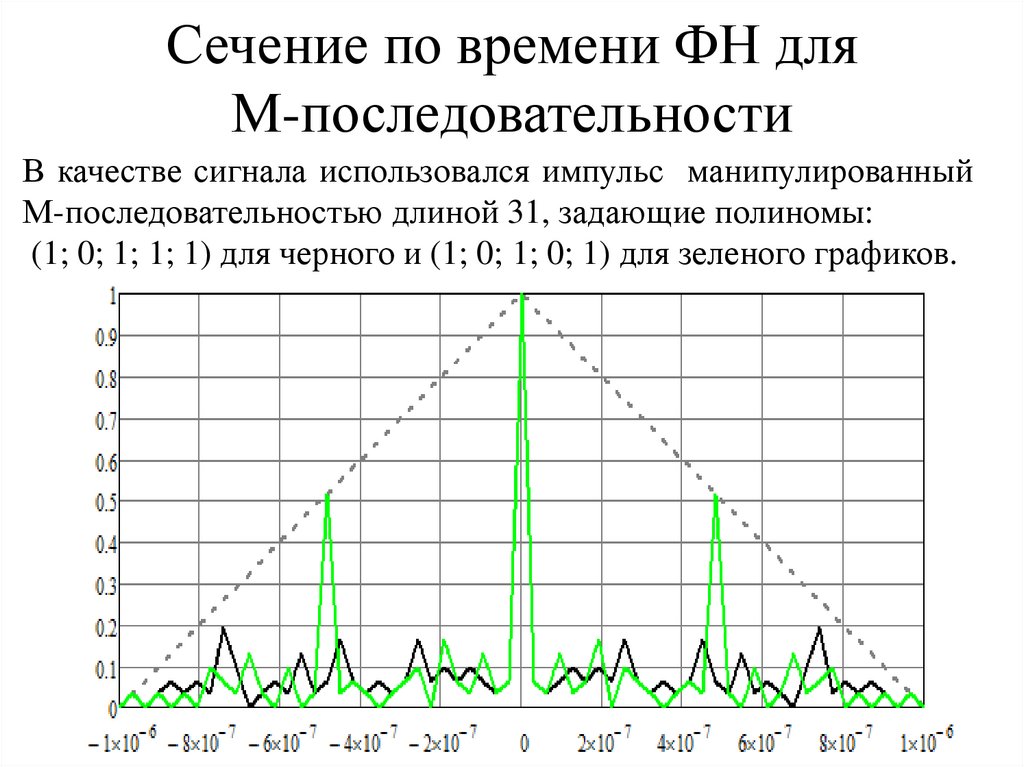
Сечение по времени ФН для
М-последовательности
В качестве сигнала использовался импульс манипулированный
М-последовательностью длиной 31, задающие полиномы:
(1; 0; 1; 1; 1) для черного и (1; 0; 1; 0; 1) для зеленого графиков.

15.

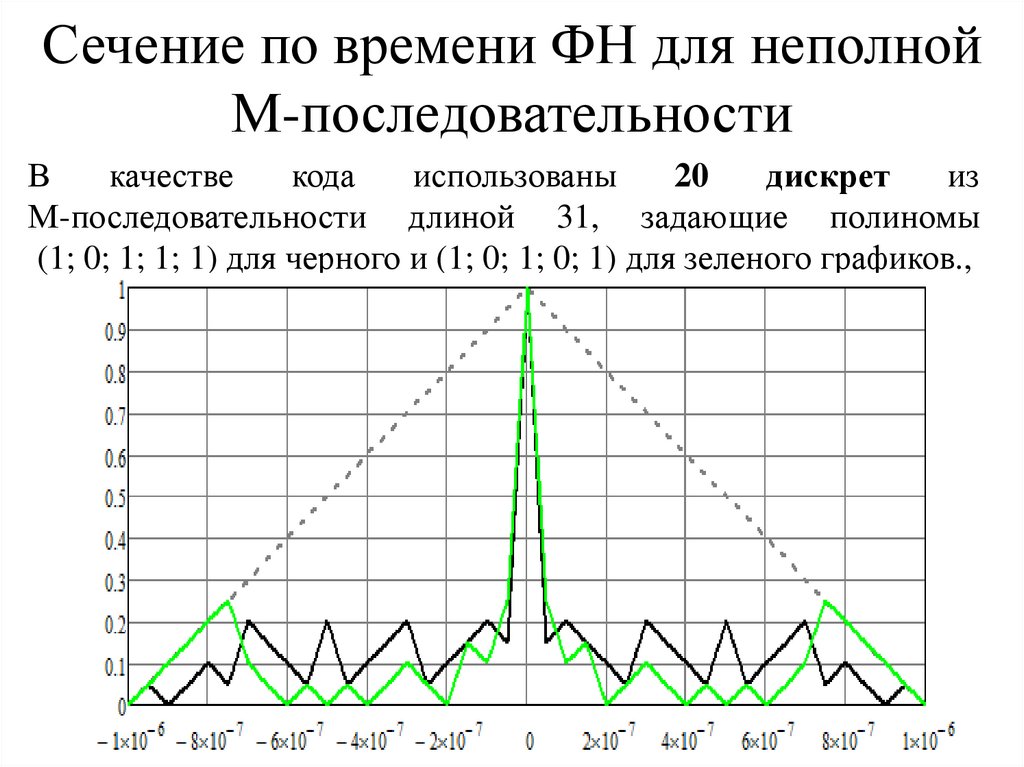
Сечение по времени ФН для неполной
М-последовательности
В
качестве
кода
использованы
20
дискрет
из
М-последовательности длиной 31, задающие полиномы
(1; 0; 1; 1; 1) для черного и (1; 0; 1; 0; 1) для зеленого графиков.,

16.

Свойства ФН ФКМ сигнала
Независимо от кода, функция неопределенности ФКМ сигнала
обладает осевой и центральной симметрией.
Предсказать поведение боковых лепестков при рассогласовании по
времени и частоте достаточно сложно, но их уровень не превышает
указанных максимальных значений.
Также независимо от кода сечение по оси частот ФКМ импульса
соответствует выражению sin(x)/x и соответствует сечению
немодулированного сигнала с той же длиной импульса,
аналогичным образом ведет себе сечение по частоте для пачечного
ФКМ сигнала.
Применение весовой обработки для пачечного сигнала допустимо
только по частоте.
Запрет применения весовых окон для импульса или непрерывного
участка кода обусловлен нарушением постулатов Голомба, так как
вес каждого дискрета в последовательности будет искажаться.

17.

Задачи
1. Определить, на какой длине волны должна работать РЛС с τ0=100 нс и
использующая 64-х элементный ФКМ сигнал, чтобы обеспечить разрешение
по скорости 20 м/с.
2. РЛС
излучает
ФКМ-радиоимпульс,
состоящий
из
255
элементов
последовательности, с длительностью дискрета τ0= 10 нс. Найти ширину
спектра радиосигнала и разрешающую способность по дальности и частоте.
3. Найти длину кода ФКМ радиосигнала, с τ0 = 1 мкс, при которой
обеспечивается
разрешение
по
частоте
ΔF = 100 Гц,
определить
разрешающую способность по дальности и скорости, если длина волны 3 см.
4. Необходимо найти разрешение по скорости и длительность импульса, если
РЛС обеспечивает разрешение по дальности Δr = 10 м, при известной длине
волны λ = 10 см и излучаемом одиннадцатиэлементном ФКМ сигнале.

18.

5. Определить максимальный уровень боковых лепестков по дальности,
разрешающую способность по дальности и скорости ФКМ радиоимпульса
представляющего
собой
М-последовательность
длиной
1023
при
длительности дискрета 100 нс и длине волны λ = 10 см.
6. Найдите длительность сжатого импульса на выходе оптимального
фильтра, если длительность ФКМ-сигнала на входе 100 мкс, а ширина
спектра 100 МГц. Определите разрешающую способность по задержке и
частоте.
7. Рассчитайте разрешающую способность РЛС по дальности и радиальной
скорости, обеспечиваемую при приеме пачки когерентных прямоугольных
ФКМ-радиоимпульсов. Число импульсов М = 20, частота повторения
импульсов f = 0,5 кГц, длительность импульсов 50 мкс, число дискрет в
одном импульсе 1023, длина волны λ = 10 см.

19.

8. Сигнал представляет из себя пачку из М = 60 ФКМ импульсов
длительностью 80 мкс с периодом повторения 400 мкс. Определить
разрешающую
способность
по
радиальной
скорости
и
длину
последовательности, если разрешающая способность по дальности 150 м.
9. В РЛС используется сигнал в виде когерентной пачки ФКМ импульсов.
Длительность импульсов 80 мкс, длина волны колебаний λ = 5 см, длина
последовательности 1023, разрешающая способность по частоте Доплера
100 Гц. Определить разрешающую способность по дальности и радиальной
скорости, длительность пачки и число импульсов.
10. Изобразить вид сечения автокорреляционной функции ρ(τ,F) плоскостью
F =0, τ=0, ρ(τ,F) = 0,5 пачки из пяти ФКМ радиоимпульсов длительностью
100 мкс с числом дискрет равным 100 и периодом повторения импульсов
Tп =500 мкс.