Энергия, переносимая электромагнитной волной. Вектор Умова-Пойнтинга

1. Энергия, переносимая электромагнитной волной. Вектор Умова-Пойнтинга.

Энергия, переносимая
1.6.
электромагнитной волной.
Вектор Умова-Пойнтинга.

2.

1.6. Вектор Умова-Пойнтинга.
Известно, что плотность энергии электрического поля
wE
E D E
2
0
2
2
а плотность энергии магнитного поля
wM
,
H B H
0
2
2
2
.
Эти выражения можно получить из уравнений Максвелла. Рассмотрим
уравнения:
B
rotE ,
(1)
t
D
(2)
rotH j
.
t
Умножим уравнение (1) на вектор H скалярно, а уравнение (2)
умножим скалярно на вектор E.

3.

1.6. Вектор Умова-Пойнтинга.
Первое уравнение системы:
B
H , rotE H , .
t
Если магнитная проницаемость постоянна,
Правая часть:
H
H , rotE 0 H ,
.
t
2
H 1 H
H
;
t 2 t
2
2
H
H
H
1
1 BH
1
.
0 H ,
0
0
2 t
2 t
t
2 t
Теперь это уравнение можно переписать так:
BH
H , rotE
.
t 2

4.

1.6. Вектор Умова-Пойнтинга.
Аналогично преобразуем второе уравнение системы:
D
rotH j
.
t
Мы рассматриваем непроводящую среду, поэтому j = 0.
1 E 2 1 ED
D
E
ED
.
E, rotH E,
0 E, 0 2 t
2 t
t 2
t
t
Итого, мы получили два уравнения:
BH
H , rotE
,
t 2
ED
E , rotH
.
t 2
Вычтем из второго уравнения первое:

5.

1.6. Вектор Умова-Пойнтинга.
ED
BH
E , rotH H , rotE
,
t 2
t 2
ED BH
E , rotH H , rotE
.
t
2
Из векторного анализа известно тождество:
div A, B B, rotA A, rotB .
Применив это тождество, получим:
E, rotH H , rotE div H , E ,
ED BH
div H , E
.
t
2

6.

1.6. Вектор Умова-Пойнтинга.
ED BH
div H , E
.
t
2
Выясним физический смысл полученного выражения. Обозначим
S E , H
- вектор Умова-Пойнтинга.
ED BH w
2
EM
- плотность энергии электромагнитного
поля.
Преобразуем левую часть уравнения:
div H , E div E , H divS .
divS
wэм
.
t
(1)

7.

1.6. Вектор Умова-Пойнтинга.
wEM
(1)
.
t
Применим к левой части уравнения (1) теорему Остроградского-Гаусса:
divS
divSdV Sd .
V
Здесь - поверхность, окружающая объём V.
Чтобы равенство не нарушилось, вычислим интеграл по объёму V и в
правой части (1):
w
EM
t
V
dV
t
WEM .
Здесь WЕМ - энергия электромагнитного поля в объёме V.
Итого, получилось:
WEM .
t
Sd WEM .
t
Sd

8.

1.6. Вектор Умова-Пойнтинга.
Sd
WEM .
t
Таким образом, поток вектора Умова-Пойнтинга через некоторую
замкнутую поверхность равен убыли энергии электромагнитного
поля в объёме, ограниченном этой замкнутой поверхностью.
S E , H .
S E H.
Таким образом,
Эти векторы образуют правую тройку.
Так как E и H лежат в плоскости,
перпендикулярной
направлению
распространения волны, направление
S
совпадает
с
направлением
распространения волны.
Согласно определению,

9. Энергия, переносимая электромагнитной волной.

1.7. Энергия, переносимая
электромагнитной волной.

10.

1.7. Энергия, переносимая электромагнитной
волной.
Как было показано ранее, плотность энергии электромагнитного поля
ED BH w
EM
2
Если в пространстве распространяется электромагнитная волна, то в
данной точке пространства
0 E 0 H .
H
0
E.
0
Плотность энергии магнитного поля
wм
H , B H
0
2
2
2
2
0 0
0 E 2
E
2 0
2
В любой момент времени
wM wE .
E, D w .
2
E

11.

1.7. Энергия, переносимая электромагнитной
волной.
wэм
ED BH H
EH
2
0
2
2
0 0
2
0
EH
2
2
0 E 2
2
0 0
2
0
0 H
0
E 0
E 0
H
0
2
0
2
EH
2
0 0 0 0
1
0 0 EH EH .
v
Здесь v – скорость электромагнитной волны в данной среде. В
вакууме, когда v = c,
1
wEM EH .
c
В некоторой среде
1
wEM EH .
v

12.

1.7. Энергия, переносимая электромагнитной
волной.
Введём новую величину, S, и назовём её модулем плотности потока
энергии. Эта величина будет равна энергии, проходящей через
единицу площади в единицу времени
W
S
,
t
W – энергия, - площадь, t – время.
W wэмV wэм vt.
W wэм vt
S
wэм v.
t
t
1
S wэм v EHv EH E , H S .
v
Модуль плотности потока энергии (эта величина равна энергии,
проходящей через единицу площади в единицу времени) равен
модулю вектора Умова – Пойнтинга.

13.

1.7. Энергия, переносимая электромагнитной
волной.
Энергия электромагнитной волны, проходящая через единицу
площади в единицу времени, равна модулю вектора Умова –
Пойнтинга.
W
E , H S .
t

14. Интенсивность излучения. Освещённость.

1.8. Интенсивность излучения.
Освещённость.

15.

1.8. Интенсивность излучения. Освещённость.
Под интенсивностью излучения понимают среднюю мощность
электромагнитной волны, проходящую через единицу площади
поверхности.
W P
E , H .
t
Мгновенное значение мощности
P E , H .
Для плоской электромагнитной волны мгновенное значение мощности
P(t ) E, H EH E0 cos( t kx ) H 0 cos( t kx )
0 E 0 H .
E02
2
E
0
0
cos 2 ( t kx )
2
0
0
1 cos(2 t 2kx 2 ) .
0

16.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
Итак, мгновенная мощность, перенесённая ЭМВ через поверхность
площади S за время t равна
E02 0
P(t )
1 cos(2 t 2kx 2 ) .
2
0
Рассматриваем площадку, расположенную в определённой точке оси
OX и перпендикулярную ей. Значение координаты x фиксировано.
P(t ) P0 1 cos(2 t ) ,
0
,
0
E02
P0
2
2kx0 2 .
Средняя мощность за время наблюдения τ
P( )
W (t )
1
1
P(t )dt P 1 cos(2 t ) dt.
0
0
0

17.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
фс
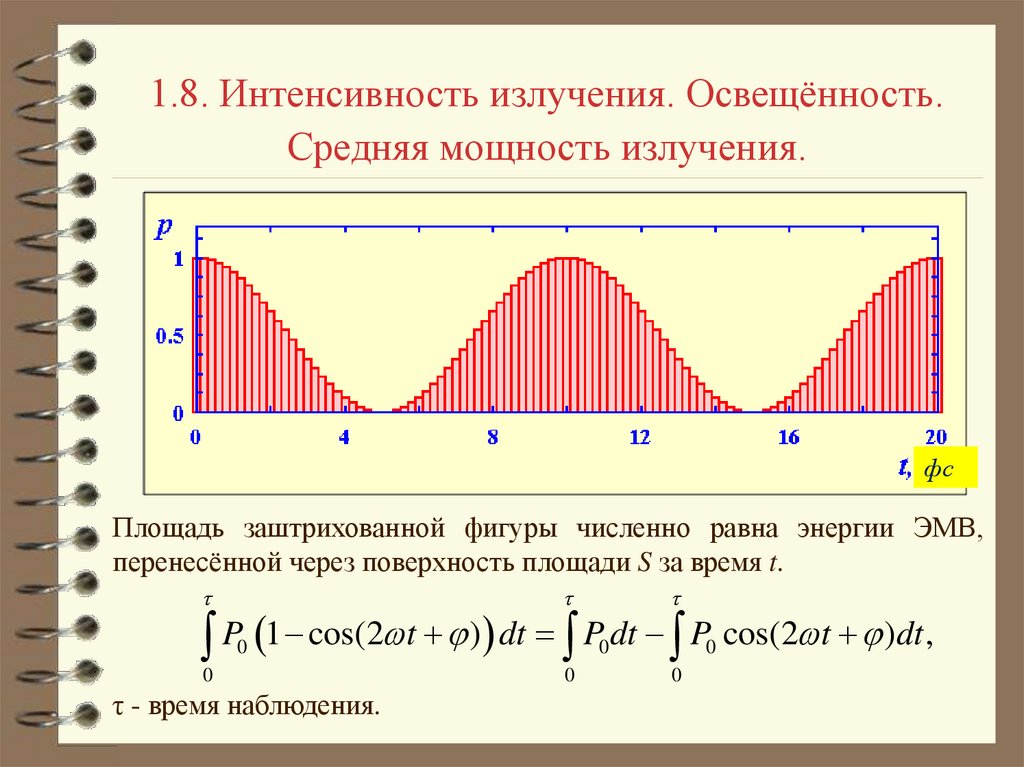
Площадь заштрихованной фигуры численно равна энергии ЭМВ,
перенесённой через поверхность площади S за время t.
P 1 cos(2 t ) dt P dt P cos(2 t )dt ,
0
0
τ - время наблюдения.
0
0
0
0

18.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
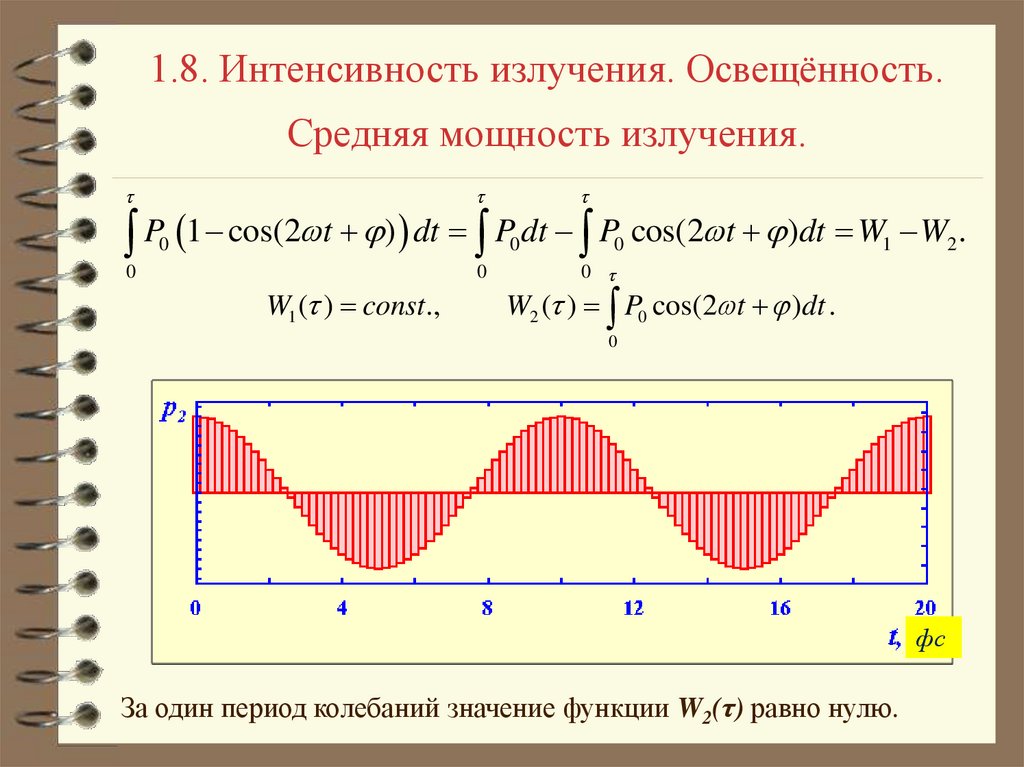
P 1 cos(2 t ) dt P dt P cos(2 t )dt W W .
0
0
0
0
W1 ( ) const.,
0
1
2
0
W2 ( ) P0 cos(2 t )dt .
0
фс
За один период колебаний значение функции W2(τ) равно нулю.

19.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
фс
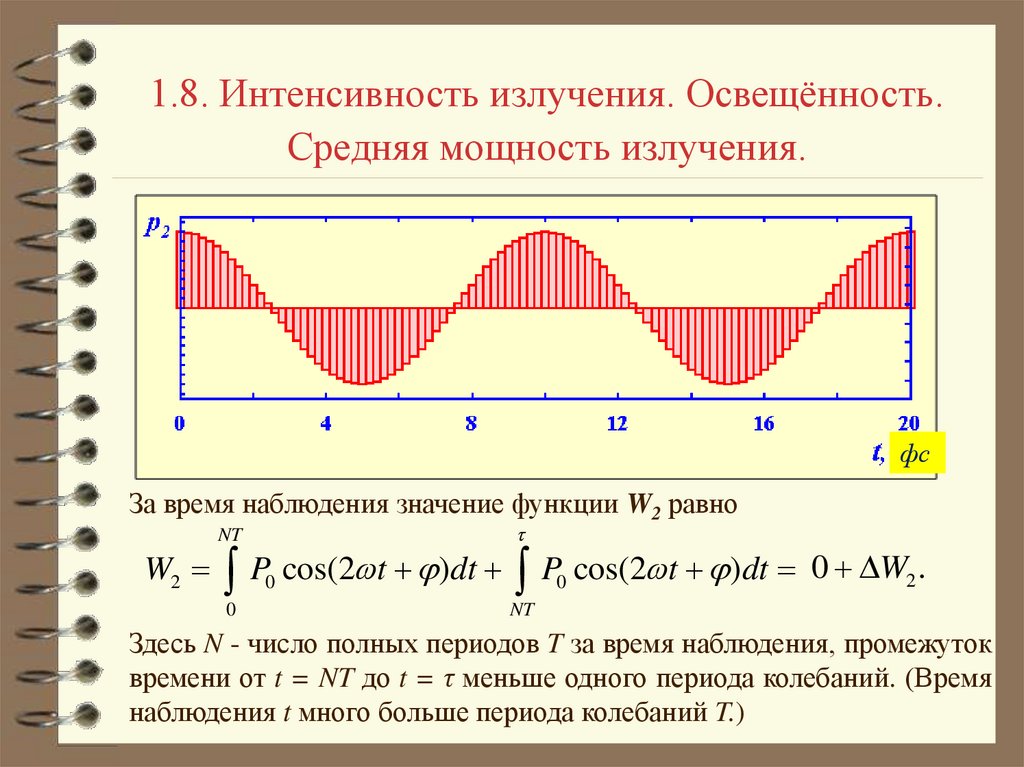
За время наблюдения значение функции W2 равно
NT
W2
P cos(2 t )dt P cos(2 t )dt
0
0
0
0 W2 .
NT
Здесь N - число полных периодов T за время наблюдения, промежуток
времени от t = NT до t = τ меньше одного периода колебаний. (Время
наблюдения t много больше периода колебаний T.)

20.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
Средняя мощность за время наблюдения τ:
P( )
P0
1
W1 W2
P0 1 cos(2 t ) dt
0
W2
P0
W2
P0 ,
так как интеграл ΔW2 вычисляется за очень короткое время (меньше
периода колебаний), а в знаменателе - очень большое время (время
наблюдения τ).
E02
Pcp P0
2
0
2
A
E0 ,
0
E02
A
.
2

21.

1.8. Интенсивность излучения. Освещённость.
Средняя мощность излучения.
Краткие выводы:
Если период колебаний в электромагнитной волне много меньше
времени усреднения, то
E02 0
2
Pcp
A
E0 .
2
0
Для подавляющего большинства диэлектриков μ = 1.
Pcp A E02 AnE02 ,
где n – показатель преломления среды.

22.

1.8. Интенсивность излучения. Освещённость.
То есть средняя мощность излучения, а с ней и интенсивность
излучения
Pcp I (t ) nE02
nH 02 .
В оптике считается, что освещённость равна средней мощности
излучения, падающего на единицу площади поверхности, поэтому
она пропорциональна квадрату напряженности электрического поля
волны, умноженного на показатель преломления среды.

23. Отражение и преломление электромагнитных волн.

2. Отражение и преломление
электромагнитных волн.
2.1. Нормальное падение волны
на границу раздела двух сред.

24.

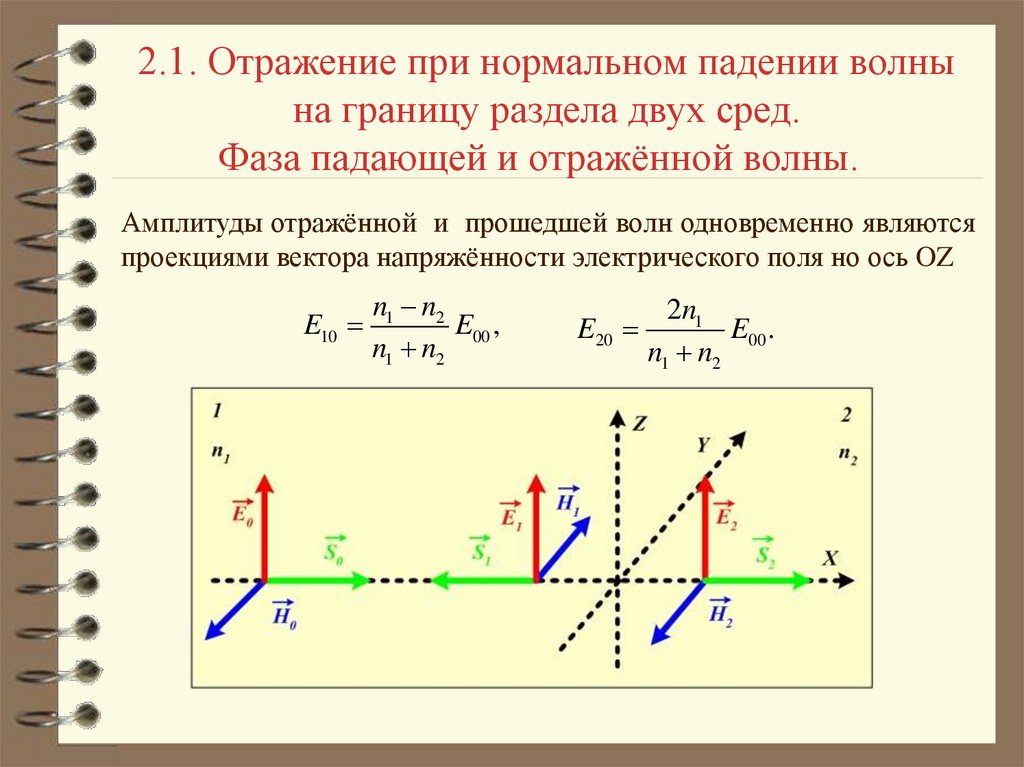
2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Рассмотрим границу раздела двух однородных,
электрически нейтральных, непроводящих сред.
1 const.;
2 const.;
1 2 ;
изотропных,
1 2 const. 1.
Из среды 1 с ε = ε1 на границу раздела падает электромагнитная
(световая) волна. Из опыта известно, что такая волна частично
отражается от границы раздела, а частично проходит во вторую среду
с ε = ε2 .
1. Изменяется ли скорость и частота волны пре переходе из одной
среды в другую?
2. Как изменяется фаза волны при отражении?
3. Требуется также определить, как относятся интенсивности
отражённой и падающей волн, а также прошедшей и падающей волн.

25.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
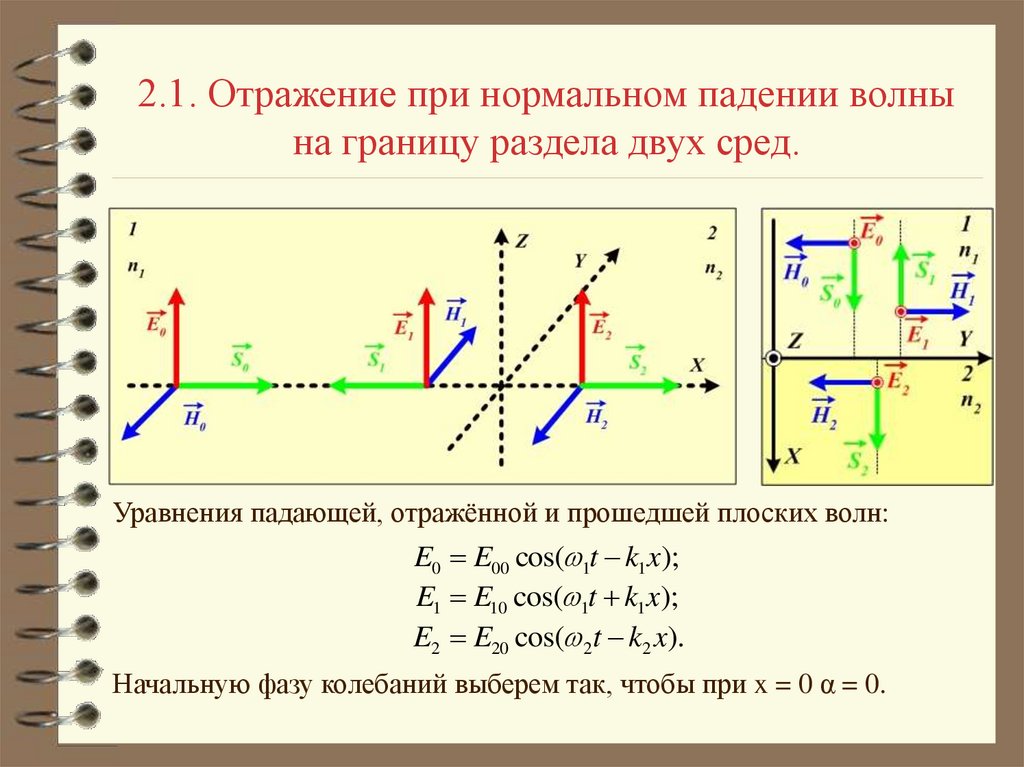
Уравнения падающей, отражённой и прошедшей плоских волн:
E0 E00 cos( 1t k1 x);
E1 E10 cos( 1t k1 x);
E2 E20 cos( 2t k2 x).
Начальную фазу колебаний выберем так, чтобы при x = 0 α = 0.

26.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Амплитуды
электрической
и
магнитной составляющих каждой
из волн связаны соотношениями ( 1
= 2 = 1):
0 E0 0 H 0 .
H 00
1 0
E00 ;
0
H10
1 0
E10 ;
0
H 20
2 0
E20 .
0
Можно считать, что точка x = 0 принадлежит как первой среде, так и
второй. В первой среде существуют падающая волна и отражённая
волна, во второй – прошедшая. Поэтому, согласно принципу
суперпозиции электрических полей для проекций вектора
напряжённости на ось OZ
E0 E1 E2 .

27.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Рассуждая
аналогично,
для
проекций вектора напряжённости
магнитного поля на ось OY
получим:
H 00 H10 H 20 .
Итак, на границе раздела сред для векторов напряжённостей полей
справедливы два уравнения:
E0 E1 E2 ,
H 0 H1 H 2 .
Подставим в первое уравнение выражения для E0, E1, E2:
E00 cos( 1t k1 x) E10 cos( 1t k1 x) E20 cos( 2t k2 x).

28.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
E00 cos( 1t k1 x) E10 cos( 1t k1 x) E20 cos( 2t k2 x).
Мы рассматриваем точку x = 0, поэтому
E00 cos( 1t ) E10 cos( 1t ) E20 cos( 2t ).
Это равенство должно выполняться в любой момент времени,
поэтому
1 2 .
При переходе через границу раздела, либо при отражении от
границы раздела частота ЭМВ не изменяется.
Скорость ЭМВ при переходе через границу раздела изменяется,
c
c
c
c
v1
,
v2
.
n1
n2
1
2

29.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Скорость ЭМВ при переходе через границу раздела изменяется,
c
c
c
c
v1
,
v2
.
n1
n2
1
2
Поэтому такие параметры волны, как волновое число и длина волны
также изменятся:
k1
1
v1
n1
2 v1
,
k2
2 c
,
n1
2
c
v2
n2
2 v2
c
.
2 c
.
n2
Чтобы определить, как изменятся амплитуды отражённой и
прошедшей волн, вернёмся к записанной ранее системе уравнений.

30.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
E00 E10 E20 ,
H 00 H10 H 20 .
H 00
1 0
E00 ;
0
H10
1 0
E10 ;
0
H 20
2 0
E20 .
0
Подставим во второе уравнение выражения для H0, H1, H2:
1 0
E00 1 0 E10 2 0 E20 .
0
0
0
2
E00 E10
E20 .
1
2 n2
,
1 n1
E00 E10
n2
E20 .
n1

31.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
E00 E10 E20 ,
H 00 H10 H 20 .
Теперь систему уравнений можно переписать так:
Сложим два уравнения:
E00 E10 E20 ,
n
E00 E10 2 E20 .
n1
n2
E20 E20 .
n1
n2
2E00 E20 1 .
n1
E00 E10 E00 E10
2n1
E20
E00
n1 n2
- амплитуда прошедшей волны.

32.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Второе уравнение системы:
Подставим в него выражение для E20:
E00 E10
n2
E20 .
n1
2n1
E20
E00 .
n1 n2
E00 E10
n2 2n1
E00 ,
n1 n1 n2
2n2
E10 1
E00 ,
n1 n2
n1 n2 2n2
E10
E00 ,
n1 n2
E10
n1 n2
E00
n1 n2
- амплитуда отражённой волны.

33.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Итак, амплитуды отражённой и прошедшей волн равны
E10
n1 n2
E00 ,
n1 n2
E20
E10 n1 n2
,
E00 n1 n2
2n1
E00 .
n1 n2
E20
2n1
.
E00 n1 n2
Относительная интенсивность отражённой волны
2
2
I1 n1 E10 n1 n2
.
I 0 n1 E00 n1 n2
Относительная интенсивность прошедшей волны
2
2
I 2 n2 E20 n22 2n1
4n1n2
.
2
2
I 0 n1E00 n1 n1 n2 n1 n2

34.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Фаза падающей и отражённой волны.
Амплитуды отражённой и прошедшей волн одновременно являются
проекциями вектора напряжённости электрического поля но ось OZ
E10
n1 n2
E00 ,
n1 n2
E20
2n1
E00 .
n1 n2

35.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Фаза падающей и отражённой волны.
n1 n2
E00 .
n1 n2
Если n1 n2 , E10 и E00
имеют одинаковые знаки
(см. рисунок).
E10
n1 n2
Это означает, что фазы колебаний отражённой волны и падающей
волны в точке падения совпадают.
Среда с большим показателем преломления называется оптически
более плотной, а среда с меньшим показателем преломления –
оптически менее плотной.
При отражении от оптически менее плотной среды фаза
отражённой волны не меняется.

36.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
Фаза падающей и отражённой волны.
n1 n2
E00 .
n1 n2
Если n1 n2 , E10 и E00
имеют разные знаки (см.
рисунок).
E10
n1 n2
Это означает, что фазы колебаний отражённой волны и падающей
волны в точке падения отличаются на π.
E0 cos t E0 cos t .
При отражении от оптически более плотной среды фаза
отражённой волны изменяется на π.

37.

2.1. Отражение при нормальном падении волны на
границу раздела двух сред. Основные результаты.
1. При переходе через границу раздела, либо при отражении от
границы раздела частота ЭМВ не изменяется.
2. Скорость ЭМВ при переходе через границу раздела изменяется,
c
c
c
c
v1
,
v2
.
n1
n2
1
2
3. Волновое число и длина волны также изменяются:
k1
1
v1
n1
2 v1
,
k2
2 c
,
n1
2
c
v2
n2
2 v2
c
.
2 c
.
n2

38.

2.1. Отражение при нормальном падении волны на
границу раздела двух сред. Основные результаты
4. Относительная интенсивность отражённой волны
2
I1 n1 n2
.
I 0 n1 n2
5. Относительная интенсивность прошедшей волны
I2
4n1n2
.
2
I 0 n1 n2
(n1 и n2 – показатели преломления сред)
6. При отражении от оптически менее плотной среды фаза
отражённой волны не меняется.
7. При отражении от оптически более плотной среды фаза
отражённой волны изменяется на π.

39.

2.1. Отражение при нормальном падении волны на
границу раздела двух сред. Задача №1.
Задача. Как изменяется интенсивность света, проходящего через
окно с двумя стёклами? Будем предполагать, что свет падает
перпендикулярно стеклу. Показатель преломления стекла n2 = 1,5;
показатель преломления воздуха n1 = 1,0.
Решение. Относительная интенсивность волны, отражённой от
границы раздела стекла и воздуха
2
2
2
E
I1
n n
1, 0 1,5
I1 0,04I 0 .
10 1 2
0, 04.
I 0 E00 n1 n2 1, 0 1,5
Относительная интенсивность волны, прошедшей в стекло из
воздуха
I 2 I 0 0,04I 0 0,96I 0 .
I1 I 2 I 0 ,
При выходе волны из стекла в воздух снова отражается 0,04 от
интенсивности падающей на границу волны, следовательно
I 3 0,96 I 2 0,962 I 0 0,9216 I 0 .

40.

2.1. Отражение при нормальном падении волны
на границу раздела двух сред.
При прохождении второго стекла интенсивность света снова
ослабляется:
I4
0,962 0,9216.
I3
Окончательно, на выходе из второго стекла
I 4 0,9216 I 3 0,9216 I 0 0,85 I 0 .
2
Задание. Решить эту задачу в общем виде. Определить, при
прохождении какого наименьшего числа стёкол (пренебрегая
поглощением) свет ослабнет более, чем в 2 раза.