Similar presentations:
Моделирование. Математические модели в биологии
1. Моделирование
1Моделирование
§ 11. Математические модели
в биологии
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
2. Модель неограниченного роста (Т. Мальтус)
Моделирование, 11 класс2
Модель неограниченного роста (Т. Мальтус)
N 0 – начальная численность
N i – численность через i периодов
рождаемость
смертность
N i 1 N i k p N i kc N i
Ni 1 (1 K ) Ni
N
K 0
K 0
N0
K 0
K=kp - kc
0
Особенности модели:
1) не учитывается влияние численности N и внешней
среды на K
2) не учитывается влияние других видов на K
К.Ю. Поляков, Е.А. Ерёмин, 2018
i
http://kpolyakov.spb.ru
3. Модель ограниченного роста (П. Ферхюльст)
Моделирование, 11 класс3
Модель ограниченного роста (П. Ферхюльст)
L – предельная численность животных
Ni 1 (1 K L ) Ni
Идеи:
1) коэффициент прироста KL зависит от численности N
2) при N=0 должно быть KL=K (начальное значение)
3) при N=L должно быть KL=0 (достигнут предел)
L Ni
N i 1 1 K
Ni
L
!
Модель адекватна,
если ошибка < 10%!
N
L
N0
i
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
4. Модель с отловом
Моделирование, 11 класс4
Модель с отловом
рыбоводческое хозяйство, разведение пушных зверей, …
L Ni
N i 1 1 K
Ni R
L
?
Какая будет численность? L?
N i N i 1, прирост = отлову
L N
N N K
N R
L
K
2
N K N R 0
L
?
отлов
Сколько можно вылавливать?
К.Ю. Поляков, Е.А. Ерёмин, 2018
N
L
N0
i
http://kpolyakov.spb.ru
5. Модель «хищник-жертва»
Моделирование, 11 класс5
Модель «хищник-жертва»
Модель – не-система:
щуки
караси
L Ni
N i 1 1 K
Ni
L
Z i 1 1 D Z i
вымирают
без еды
Модель – система:
1) число встреч пропорционально Ni Zi
2) «эффект» пропорционален числу встреч
численность уменьшается
N i 1 (1 K L bN Z i ) N i
Z i 1 (1 D bZ N i ) Z i
численность увеличивается
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
6. Модель «хищник-жертва»
Моделирование, 11 класс6
Модель «хищник-жертва»
Хищники вымирают:
Ni
Равновесие:
караси
Ni
Zi
караси
Zi
щуки
0
щуки
i
0
i
D 0,8
D 0,8
bN bZ 0,005
bN 0,01;
К.Ю. Поляков, Е.А. Ерёмин, 2018
bZ 0,012
http://kpolyakov.spb.ru
7. Модель «хищник-жертва»
Моделирование, 11 класс7
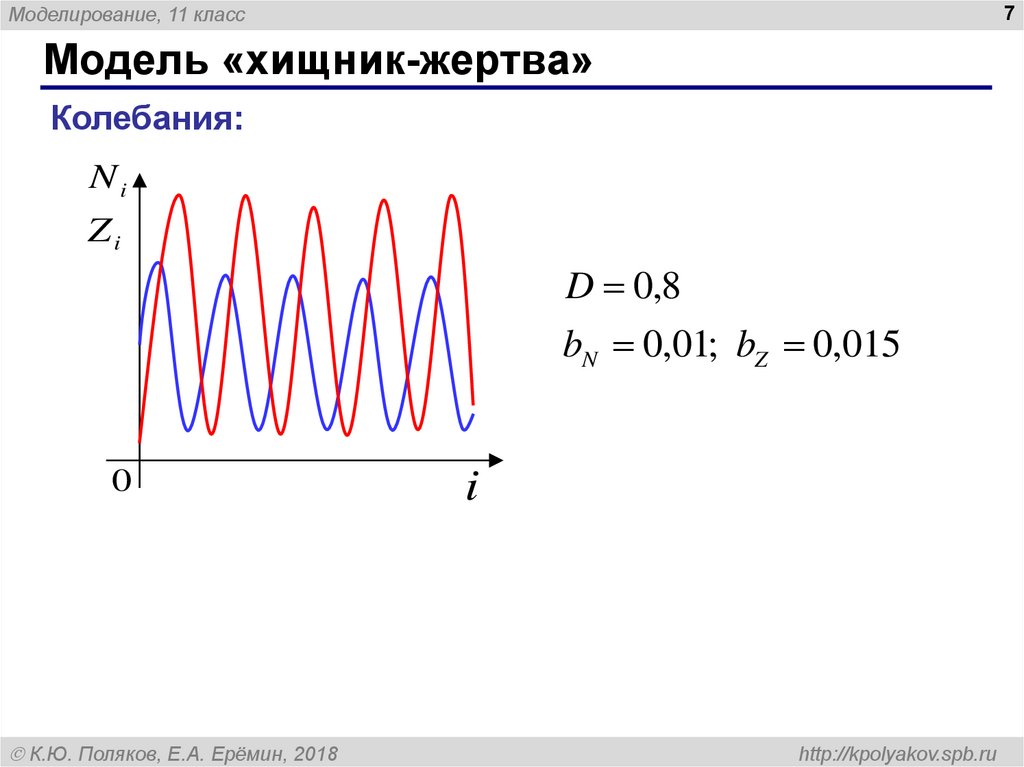
Модель «хищник-жертва»
Колебания:
Ni
Zi
D 0,8
bN 0,01; bZ 0,015
0
К.Ю. Поляков, Е.А. Ерёмин, 2018
i
http://kpolyakov.spb.ru
8. Обратная связь
Моделирование, 11 класс8
Обратная связь
Модель неограниченного роста:
K
популяция
N
Модель ограниченного роста:
L
популяция
KL
N
обратная связь
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
9. Саморегуляция
Моделирование, 11 класс9
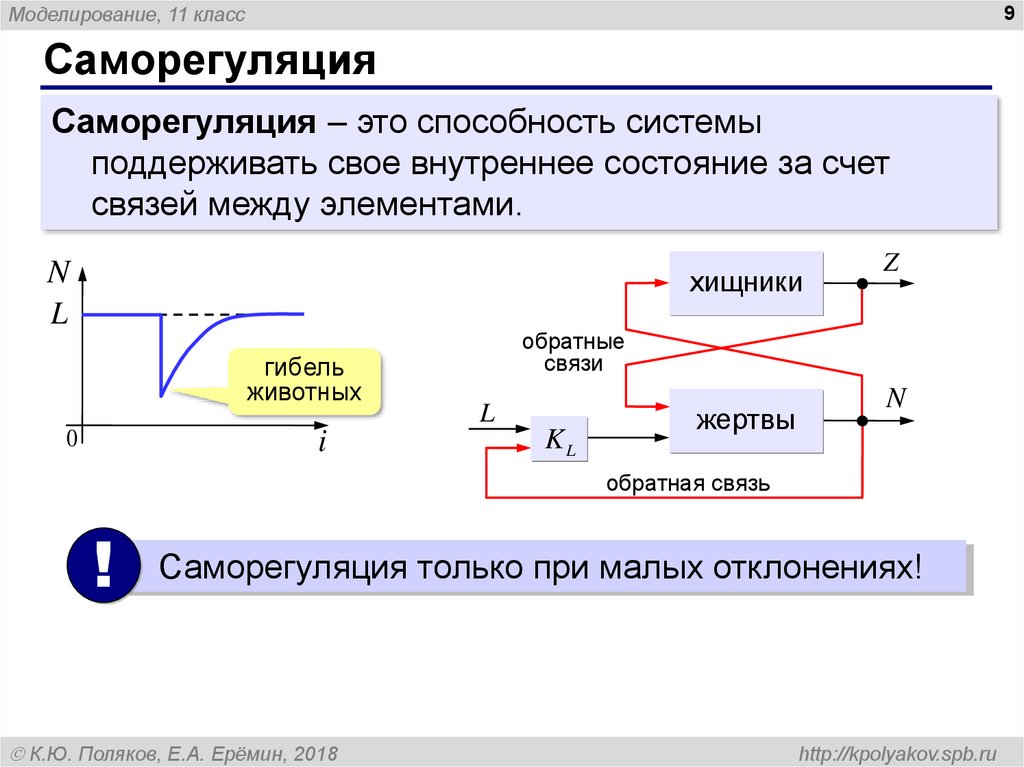
Саморегуляция
Саморегуляция – это способность системы
поддерживать свое внутреннее состояние за счет
связей между элементами.
N
L
хищники
гибель
животных
i
0
Z
обратные
связи
L
KL
жертвы
N
обратная связь
!
Саморегуляция только при малых отклонениях!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru







 mathematics
mathematics biology
biology








