4.01M

Category:

finance

Потоки платежей

1.

Потоки платежей
1. Типы потоков платежей
2. Финансовые ренты
3. Непрерывные потоки платежей, изменяющиеся во времени
4. Расчет параметров финансовой ренты
1

1. Типы потоков платежей
Потоки платежей – это платежи, последовательные во времени
(выплаты, по купонам облигаций, пенсии и т.д.)
Основные характеристики потоков платежей:
1. Регулярный поток платежей
2. Нерегулярный поток платежей
3. Наращенная сумма потока платежей
4. Современная стоимость потока платежей
2

3.

Регулярный поток платежей (финансовая рента,
аннуитет) – это платежи, у которых все выплаты направлены
в одну сторону (например, поступления), а интервалы
(периоды) между платежами одинаковы
Нерегулярный поток платежей – это платежи, у которых
часть выплат является положительной величиной
(поступления), а другая часть – отрицательной (выплаты);
Интервалы могут быть различными
3

4.

Наращенная сумма потока платежей – это сумма всех выплат
с начисленными на них к концу срока сложными процентами
Современная стоимость потока платежей – это сумма всех
выплат, дисконтированных на начало срока этого потока по
сложной процентной ставке
4

5.

Рассмотрим общий случай потока платежей
Введем обозначения:
5

6.

K
S Rk 1 i
t K tk
(2.1) – наращенная сумма
k 1
K
Rk
A
tk
1
i
k 1
(2.2) – современная стоимость
потока платежей
6

7.

Формулу (2.2) можно получить иначе (дисконтированием
наращенной суммы (2.1))
K
S
1
t K t k
Rk 1 i
tK
tK
1 i k 1
1 i
K
Rk 1 i
t k
k 1
S
A
tK
1 i
K
Rk
A
tk
k 1 1 i
(2.3) – современная стоимость
потока платежей
7

8.

9.

Решение:
1. Наращенная сумма по (2.1):
2. Современная стоимость потока платежей по (2.2):
3. Современная стоимость потока платежей по (2.3):
9

10.

2. Финансовые ренты
По моменту выплат в пределах между началом и концом
периода ренты делятся на:
1) Постнумерандо (обыкновенные), выплаты в конце периода
2) Аннуитеты пренумерандо, выплаты в начале периода
3) Ренты с платежами в середине периода
10

11.

Рассмотрим финансовые ренты постнумерандо
Постоянной называется рента, выплаты которой не
изменяются во времени
Годовая рента постнумерандо предусматривает
выплаты и начисление процентов 1 раз в конце года
11

12.

Определим наращенную сумму годовой ренты.
В течение n лет в фонд (банк) в конце каждого года вносится
по R рублей, на них начисляются сложные проценты по ставке
i% годовых (на первый взнос проценты начисляются на n-1 год,
на второй – n-2 года и т.д.:
S R 1 i
n 1
R 1 i
n 2
... R 1 i R
Справа – сумма геометрической прогрессии
со знаменателем q=1+i, первым элементом R,
количеством элементов n. Сумма вычисляется
R qn 1
по формуле:
Sn
1 i
S R
n
i
1
q 1
(2.4) – наращенная сумма годовой
ренты
12

13.

Формулу (2.4) можно переписать в виде:
S R s n ,i
s n ,i
n
1 i 1
i
(2.5)
(2.6) – коэффициент
наращения ренты
(табулированная функция)
13

14.

Для определения современной стоимости годовой ренты
проведем дисконтирование каждого платежа на начало
срока ренты и найдем общую сумму:
R
R
R
R
A
...
2
3
n
1 i 1 i 1 i
1 i
R
1
1
1
1
...
2
n 1
1 i 1 i 1 i
1 i
в скобках сумма
геометрической
прогрессии, q=1/(1+i)
1
1
n
n
n
R 1 i
1 i 1
1 1 i
R
R
1
1 i
1 1 i
i
1
1 i
14

15.

1 1 i
A R
i
n
(2.7) – современная стоимость
годовой ренты
Формулу (2.7) можно переписать в виде:
A R an ,i
(2.8)
1 1 i
i
n
a n ,i
(2.9) - коэффициент
приведения ренты
(табулированная функция)
15

16.

17.

Наиболее общий тип ренты с начислением процентов по
номинальной процентной ставке и неоднократными выплатами
в году (на рис. 2.3. - возможная схема выплат и начислений
такой ренты)
17

18.

Если выплаты производятся p раз в году, то такая рента
называется p-срочной, или рентой с неоднократными
выплатами в году
18

19.

mn
( p)
smn
; j/m
j
1 1
m
m/ p
j
p 1 1
m
p
A R amn; j / m
(2.11) - коэффициент
наращения p-срочной ренты
(табулированная функция)
(2.12) – современная стоимость
p-срочной ренты
mn
a
( p)
mn; j / m
j
1 1
m
m/ p
j
p 1 1
m
(2.13) – коэффициент
приведения p-срочной ренты
(табулированная функция)
19

20.

21.

22.

Частный случай: количество начислений процентов в году
равно количеству выплат в году (m=p)
(2.10)-(2.13)
j
1
m
S R
j
mn
1
j
1 1
m
A R
j
(2.14) - наращенная сумма
mn
(2.15) - современная стоимость
22

23.

24.

25.

Рассмотрим случай годовой ренты с начислением процентов
по номинальной процентной ставке (p=1).
(2.10)-(2.13)
mn
j
1
1
m
S R
R smn; j / m
m
j
1
1
m
(2.16) - наращенная сумма
mn
smn; j / m
j
1 1
m
m
j
1 1
m
(2.17) - коэффициент
наращения ренты
(табулированная функция)
25

26.

A R amn; j / m
amn; j / m
j
1 1
m
m
(2.18) – современная стоимость
ренты
mn
j
1 1
m
(2.19) – коэффициент
приведения ренты
(табулированная функция)
26

27.

28.

29.

Рассмотрим p-срочную ренту (m=1)
(2.10)-(2.13)
S R s
( p)
n;i
1 i 1
p 1 i 1/ p 1
n
s
( p)
n ;i
(2.20) - наращенная сумма
(2.21) – коэффициент наращения
ренты (табулированная функция)
29

30.

A R a
( p)
n;i
(2.22) – современная стоимость
ренты
1 1 i
1/ p
p 1 i 1
n
a
( p)
n ;i
(2.23) – коэффициент
приведения ренты
(табулированная функция)
30

31.

32.

Финансовые ренты пренумерандо и ренты с выплатами
в середине периодов
Расчеты характеристик аналогичны рентам постнумерандо
j
S1 S 1
m
m/ p
(2.24) - наращенная сумма
ренты пренуменрандо
S1, S - наращенная сумма ренты пренумерандо и
постнумерандо с начислением процентов по
номинальной процентной ставке и
неоднократными выплатами в году соответственно
32

33.

j
A1 A 1
m
m/ p
(2.25) – современная стоимость
ренты пренуменрандо
А1, А - современная стоимость ренты
пренумерандо и постнумерандо с начислением
процентов по номинальной процентной ставке и
неоднократными выплатами в году соответственно
33

34.

35.

36.

Рассмотрим ренту с выплатами в середине периода:
S1/ 2
j
S 1
m
m
2p
(2.26) - наращенная сумма
ренты c выплатами в
середине периода
S1/2 - наращенная сумма ренты c выплатами в
середине периода;
S - наращенная сумма ренты постнумерандо с
начислением процентов по номинальной
процентной ставке и неоднократными выплатами
в году
36

37.

A1/ 2
j
A 1
m
m
2p
(2.27) - современная стоимость
ренты c выплатами в
середине периода
А1/2 - современная стоимость ренты c выплатами в
середине периода;
А - современная стоимость ренты постнумерандо
с начислением процентов по номинальной
процентной ставке и неоднократными выплатами
в году
37

38.

39.

40.

Финансовые отложенные и вечные ренты
Отложенными называются ренты, у которых начало
выплат отложено вперед
Порядок вычислений:
1. Находят современную стоимость исходной ренты
2. Дисконтируют полученный результат к началу
отложенной ренты
40

41.

R an;i
A
t A
t
t
1 i 1 i
(2.28) - современная стоимость
годовой отложенной ренты
А - современная стоимость исходной ренты, у которой моментом
приведения считается начало выплат;
t – время задержки в выплате ренты;
an;i – коэффициент приведения ренты к началу выплат
41

42.

43.

Задача деления ренты постнумерандо между двумя
участниками
Годовая выплата R, срок n. Вначале выплаты получает первый
участник, его доля от капитализированной ренты равна x.
Второй участник получает оставшиеся платежи. Его доля 1- x.
Необходимо определить время получения первым (n1) и
вторым участниками (n2).
Решение:
Если известно время n1, то
n2=n-n1
43

44.

Из условия
A1 t A2
x 1 x
С учетом n2=n-n1, n1=t
44

45.

Прологарифмируем (2.30)
n1 ln 1 i ln 1 x x 1 i
ln 1 x x 1 i
n1
ln 1 i
n
n
(2.31) - время получения доли
первым участником
Если срок ренты очень большой или конкретно не оговаривается
(n ), то такая рента называется вечной.
45

46.

mn
Из формул
p
A R amn
; j/m
( p)
(2.12) amn
; j/m
j
1 1
m
m/ p
j
p 1 1
m
(2.13)
mn
A ( p;m)
j
1 1
R
m
lim R
m/ p
m/ p
n
j
j
p 1 1 p 1 1
m
m
(2.31) – современная
стоимость p-срочной
ренты с начислением
процентов несколько
раз в году
R – годовая выплата
j - номинальная процентная ставка
p – количество выплат в году
m – количество начислений процентов в году
46

47.

48.

49.

50.

Финансовые ренты с непрерывным начислением процентов
K
S Rk 1 i
t K tk
K
(2.1)
k 1
Rk
tk
1
i
k 1
A
(2.2)
m
j при m
S R s
( p)
n;
sn( ;p )
(2.34) – наращенная сумма
e n 1
p e / p 1
(2.35) – коэффициент наращения ренты
50

51.

Частный случай: годовая рента (p=1)
S R sn;
n
sn;
e 1
e 1
(2.36) – наращенная сумма
(2.37) – коэффициент наращения ренты
51

52.

53.

(2.12), (2.13), m :
(2.38)
A R a
( p)
n;
(2.39) - современная стоимость
p-срочной ренты с непрерывным
начислением процентов
53

54.

Частный случай: годовая рента (p=1)
A R an;
n
an;
1 e
e 1
(2.40) – современная стоимость
(2.41) – коэффициент приведения ренты
Связь между силой роста и номинальной ставкой j имеет
вид (1.9):
j
m ln 1 , j m e / m 1 .
m
54

55.

56.

Ренты с непрерывной выплатой платежей (p )
p
sn;
p
an;
s( n; )
a( n; )
n
e 1
1 e
(2.42) - коэффициент наращения ренты
n
(2.43) - коэффициент приведения ренты
56

57.

( p )
n;
S R s
( p )
n;
A R a
(2.34) – наращенная сумма
(2.45) – современная стоимость
57

58.

59.

2.5. Финансовые ренты с ежегодными изменениями выплат
на постоянную величину
Переменной рентой называется поток платежей, у которого
выплаты изменяются во времени по заданному закону, а
интервалы между выплатами постоянны
Пусть выплаты в течение n лет представлены в виде ряда (по
закону арифметической прогрессии)
R, R+a, R+2a, …, R+(n-1)a
R – выплата в конце первого года
a – постоянное годовое приращение
n – срок ренты
59

60.

Окончательно получим:
a
na
A R an;i
n
i
i 1 i
S A 1 i
n
(2.46) – современная
стоимость ренты
(2.47) – связь современной
стоимости ренты с наращенной
суммой
Подставим (2.47) в (2.46):
a
na
S R s n ;i
i
i
(2.48)
60

61.

62.

63.

2.6. Финансовые ренты с изменением выплат по закону
геометрической прогрессии
Пусть выплаты в течение n лет представлены в виде
ряда (по закону геометрической прогрессии)
R, Rq, Rq2, …, Rqn-1
R – выплата в конце первого года
q – знаменатель прогрессии
n – срок ренты
Современная стоимость такой ренты определяется
суммой:
63

64.

Если q=1+ , где - темп прироста ренты, то
(2.49) – современная
стоимость
S A 1 i
n
(2.50) – наращенная сумма
64

65.

Подставим (2.50) в (2.49):
(2.51) – наращенная
сумма
65

66.

67.

3. Непрерывные потоки платежей, изменяющиеся во
времени
67

68.

Определим наращенную сумму для момента n
при выплате в момент t:
( n t )
dS R(t )e
dt
(2.52)
- сила роста
R(t)dt – величина выплаты в момент t
dt – бесконечно малый отрезок времени
n
(2.52)
S R(t )e
0
( n t )
dt
(2.53) - наращенная сумма
непрерывного переменного
потока платежей
68

69.

n
A R(t )e dt
t
0
(2.54) – современная
стоимость непрерывного
переменного
потока платежей
(2.53), (2.54)
n
S e n R(t )e t dt
(2.55)
0
S Ae
n
(2.56) – связь между
SиA
69

70.

3.1. Непрерывные потоки платежей, изменяющиеся
по параболическому закону
Поток платежей, изменяющийся по параболическому закону,
представим в виде:
Rt=R(t)=R+at+bt2
n
a 2b
ane
A R 2 a n;
здесь
a n;
1 e n
n
bne
2
n
(2.57) – современная
стоимость
70

71.

a 2b
an bn
2
S A e R 2 s n;
n
n
(2.58) – наращенная сумма
здесь
a n; e n
1 e n
e n
e n 1
s n;
71

72.

73.

74.

3.2. Непрерывные потоки платежей, изменяющиеся
по линейному закону
Поток представим в виде: Rt=R(t)=R+at
Подставим b=0 в (2.57) и (2.58):
n
a
ane
A R a n;
(2.59) – современная
стоимость
a
an
S A e R s n;
n
(2.60) – наращенная
сумма
74

75.

76.

4. Расчет параметров финансовой ренты
Для p-срочной ренты с начислением процентов m раз в году
величина годовой выплаты определяется из формул (2.10)
и (2.12):
p
p
S
R
s
A R amn; j / m ,
mn; j / m
S
R p
smn; j / m
A
R p
amn; j / m
76

77.

78.

79.

В практической деятельности актуальны задачи определения
срока ренты (при прочих известных параметрах).
Рассмотрим общий случай – постоянная рента с
начислением процентов по номинальной процентной
ставке и неоднократными выплатами в году
mn
j
1 1
m
S R
m| p
j
p 1 1
m
(2.63) – наращенная сумма
79

80.

Найдем срок n. Для этого:
1) Представим (2.63) в виде:
(2.64)
2) Прологарифмируем (2.64):
(2.65)
80

81.

3) Решим (2.65) относительно n:
(2.66)
При расчете по (2.66) срок получается, как правило, дробным.
Количество периодов np округляют до целого числа n0.
Затем уточняют значение разового платежа:
(2.67) – уточненный
разовый платеж
81

82.

83.

84.

Частный случай: начисление процентов по номинальной
процентной ставке и неоднократными выплатами в
году
A
ln 1
R
n
m/ p
j
p 1 1
m
j
m ln 1
m
(2.68) – срок ренты
m/ p
j
1 1
R
m
A
mn
p
j 0
1 1
m
уточненный
разовый платеж
Для других типов ренты срок определяется аналогично
84

85.

86.

Если известны все параметры ренты, кроме процентной
ставки, то расчет процентной ставки можно трактовать как
определение доходности финансовой операции)
Процентную ставку рассчитывают приближенно.
Рассмотрим численный метод Ньютона-Рафсона
86

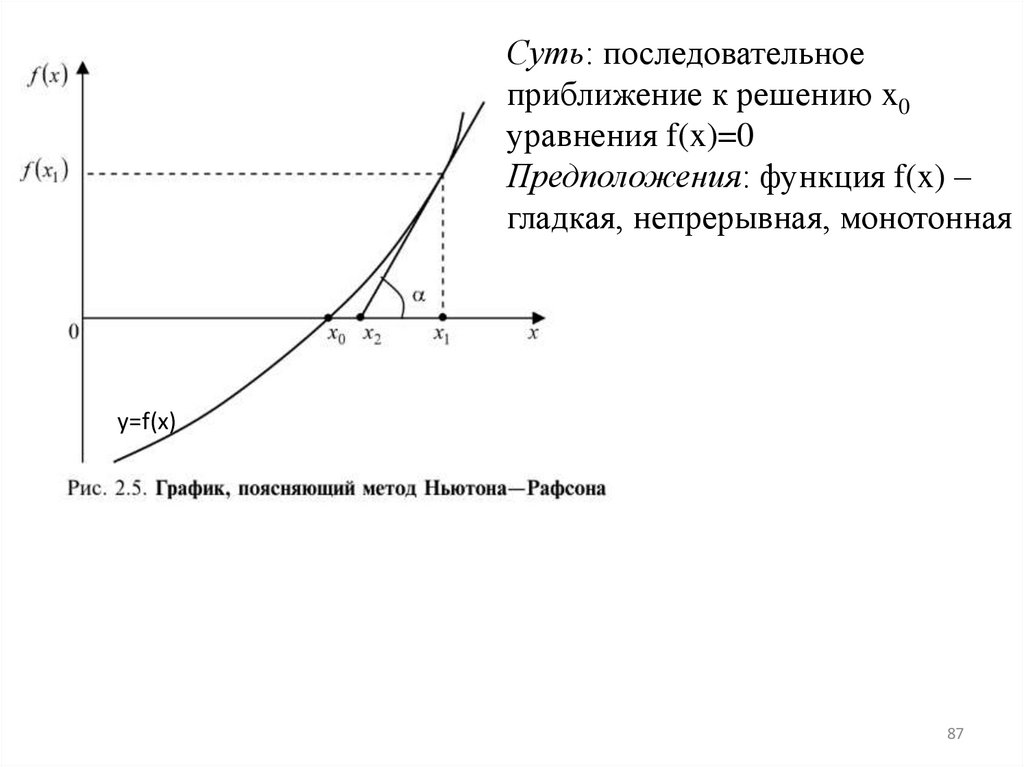
87.

Суть: последовательное
приближение к решению x0
уравнения f(x)=0
Предположения: функция f(x) –
гладкая, непрерывная, монотонная
y=f(x)
87

88.

Алгоритм:
1) ввести x1- начальное приближение, - требуемая
точность (например: 0,01; 0,001);
2) через т. (x1,f(x1)) проводится касательная к графику,
пересекающая ось ox в точке x2;
3) если |x2-x1|< , то x2 – искомый корень, иначе x2следующее приближение и переход к п.2
88