Similar presentations:
Решение задачи с использованием циклов
1.
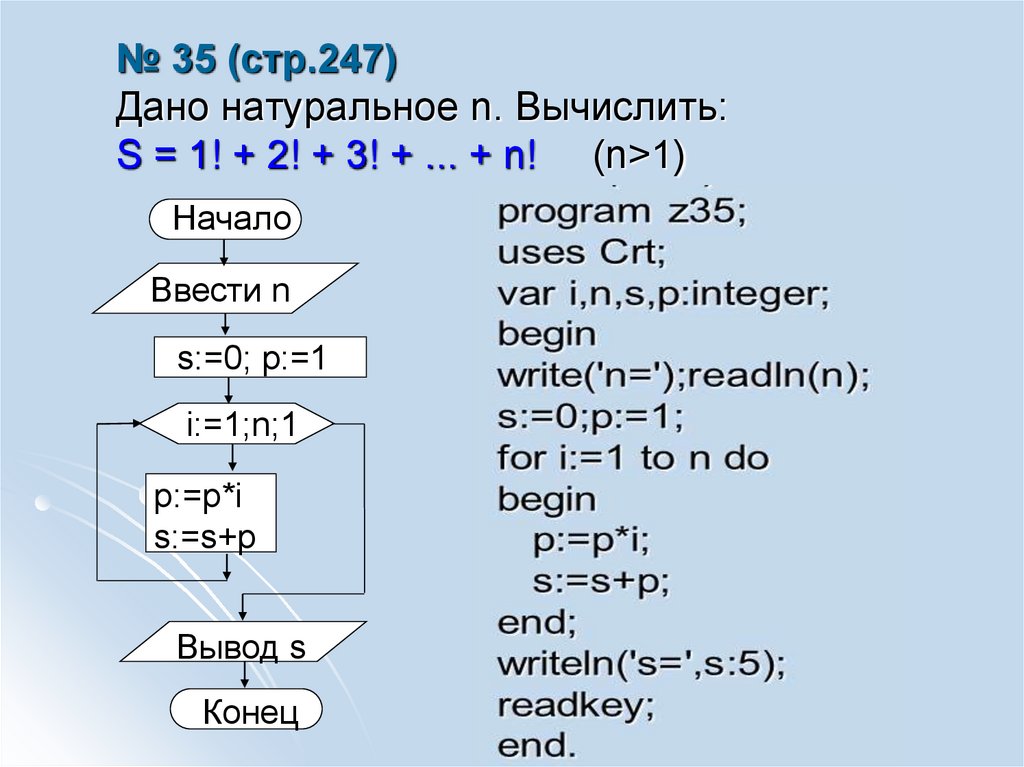
2. № 35 (стр.247) Дано натуральное n. Вычислить: S = 1! + 2! + 3! + ... + n! (n>1)
№ 35 (стр.247)Дано натуральное n. Вычислить:
S = 1! + 2! + 3! + ... + n! (n>1)
Начало
Ввести n
s:=0; p:=1
i:=1;n;1
p:=p*i
s:=s+p
Вывод s
Конец
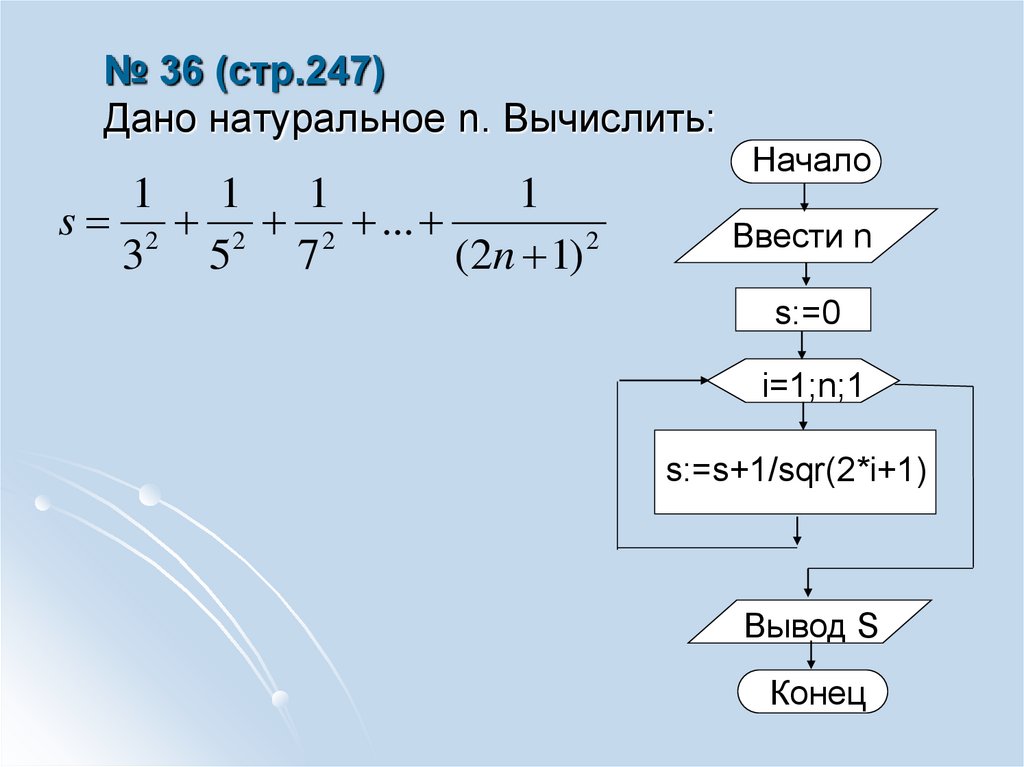
3. № 36 (стр.247) Дано натуральное n. Вычислить:
1 11
1
s 2 2 2 ...
2
3 5
7
(2n 1)
Начало
Ввести n
s:=0
i=1;n;1
s:=s+1/sqr(2*i+1)
Вывод S
Конец
4. № 37 (стр.247) Числа Фибоначчи (fn) определяются по формулам f0 = f1 = 1, fn = fn-1 + fn-2 при n = 2, 3, ... Определить f40
Началоf0:=1;f1=1
i=2;40;1
f:=f0 + f1
f0:= f1; f1:= f
Вывод f
1 1 2 3 5 8 13 ...
Конец
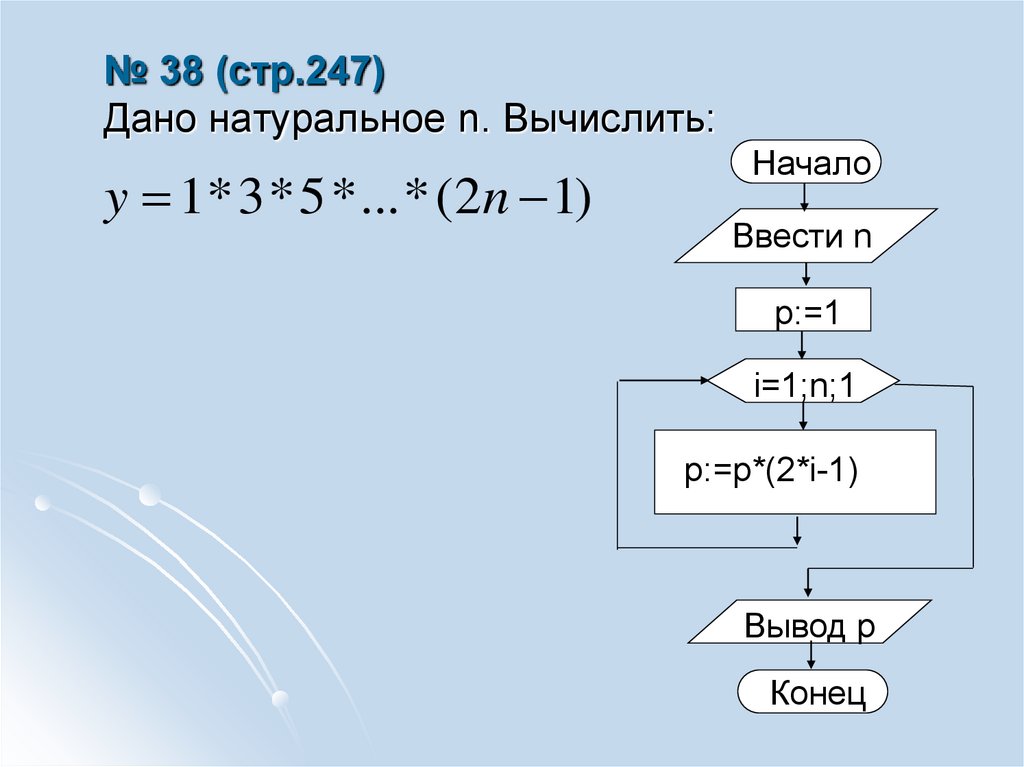
5. № 38 (стр.247) Дано натуральное n. Вычислить:
y 1* 3 * 5 * ... * (2n 1)Начало
Ввести n
p:=1
i=1;n;1
p:=p*(2*i-1)
Вывод p
Конец
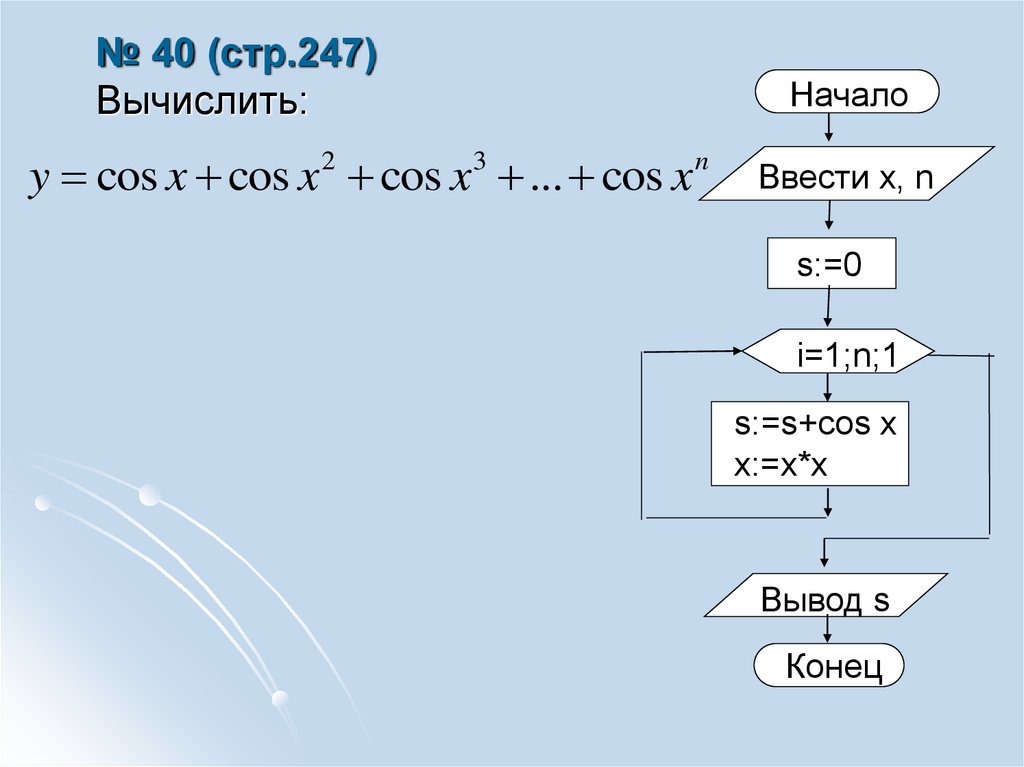
6. № 40 (стр.247) Вычислить:
y cos x cos x 2 cos x 3 ... cos x nНачало
Ввести x, n
s:=0
i=1;n;1
s:=s+cos x
x:=x*x
Вывод s
Конец
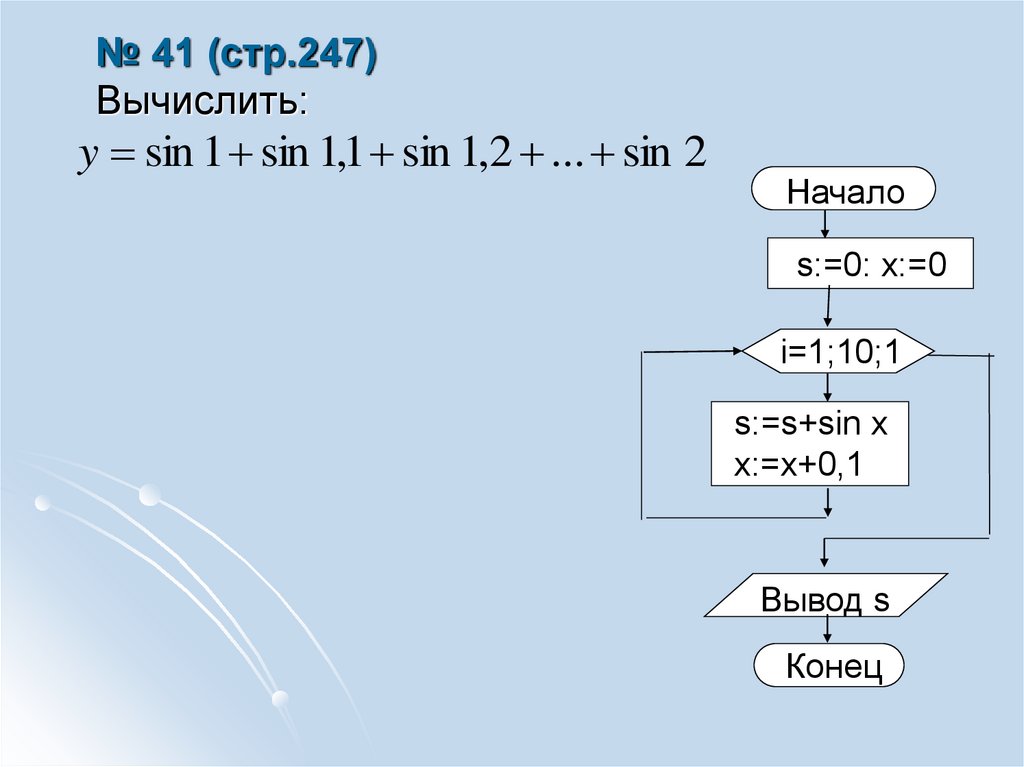
7. № 41 (стр.247) Вычислить:
y sin 1 sin 1,1 sin 1,2 ... sin 2Начало
s:=0: x:=0
i=1;10;1
s:=s+sin x
x:=x+0,1
Вывод s
Конец


 mathematics
mathematics








