Обозначение основных плоскостей проекций

1.

Омский государственный
университет путей
сообщения
КАФЕДРА: «ИНФОРМАТИКА И
КОМПЬЮТЕРНАЯ ГРАФИКА»
08.10.2021
Информация для решения
задач контрольной работы №1
1

2.

• Информация к защите КР и задачи по
теме (слайды 3 - 45);
• Возможный набор для защиты.
08.10.2021
Информация для решения
задач контрольной работы №1
2

3.

Обозначение основных плоскостей
проекций
• Для плоскостей
проекций приняты
обозначения: П1, П2, П3,
Где П1 − горизонтальная
плоскость проекций;
П2 − фронтальная
плоскость проекций;
П3 − профильная
плоскость проекций;

4.

ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
08.10.2021
Информация для решения
задач контрольной работы №1
4

5.

Построение проекций точки А в первом октанте
+z
Аz
А2
Аx
А3
x
y
OА
z
+X
Аy
А
1
08.10.2021
Информация для решения
задач контрольной работы №1
+Y
5

6.

Изображения геометрических элементо
в ортогональных проекциях
1.
Задача. Построить проекции точек по координатам, заданным в
миллиметрах (x,y,z): А(30,15,30); В(10,25,0) С(10,25,20). Совпадение
проекций в задачах обозначать по примеру: В1 ≡ С1 (горизонтальная
проекция точки В совпадает с горизонтальной проекцией точки С).
2.
На наглядном изображении и на комплексном чертеже (рис. 1)
построить профильную проекцию А3 точки А. Внести в таблицу
названия все элементов чертежа аналогично таб.1.
№ п/п
Обозначение элемента
Название элемента
чертежа
1
П1
Горизонтальная
плоскость проекций
2
АА1
Линия связи
…
x,y,z
Оси
11
A
Информация для решения задач
контрольной работы
3 №1
6
08.10.2021
Профильная проекция
точки А

7.

Не торопись листать. Слушай !!!!
z
A2
z
A2
Π2
ХА
YА
ZА
П3
ZА
ХА
o
x
A3
A
Ax
y x
YА
Ax
O
A1
y
A1
а
y
б
Рис. 1. Комплексный чертёж и наглядное изображение точки А
Информация для решения задач
контрольной работы №1
7
08.10.2021

8.

Для создания комплексного чертежа (см. рис.) для точки,
необходимо по её координатам А (45, 36,25 ) построить три её
проекции:
1. По оси х от точки О отложить абсциссу ОАх размером 45 мм;
2. Через Ах провести вертикальную линию проекционной связи,
на которой вверх отложить аппликату АхА2 = 25 мм, а вниз
ординату АхА1 = 36 мм;
3. Через А1 провести горизонтальную линию связи А1Ау. Точку
Ау перенести вправо на ось х и восстановить из неё
z
перпендикуляр до пересечения
с продолжением А2Аz
А2
А3
25
х
Аz
45
О
у
36
Ах
А1
Информация для решения задач
контрольной работы №1
Ау
у
Рис. Построение комплексного
чертежа
8
08.10.2021

9.

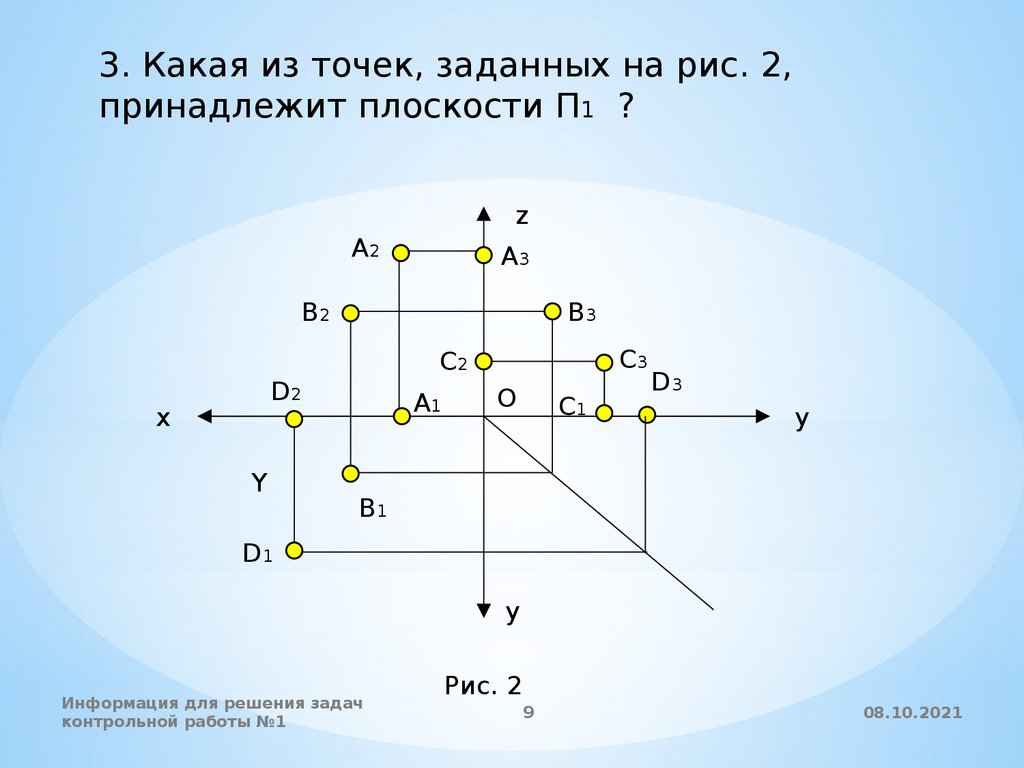
3. Какая из точек, заданных на рис. 2,
принадлежит плоскости П1 ?
z
А2
А3
В2
В3
С3
С2
D2
x
Y
А1
О
С1
D3
y
В1
D1
y
Информация для решения задач
контрольной работы №1
Рис. 2
9
08.10.2021

10.

Ответы к задаче 3 для
точки А
z
А2
ZА
А3
П3
ХА
О
А1
(x,y,0)
(x,0,z)
П1
Информация для решения задач
контрольной работы №1
(0,y,z)
y
10
∩
y
П1
∩
x
П2
∩
П2
08.10.2021
П3

11.

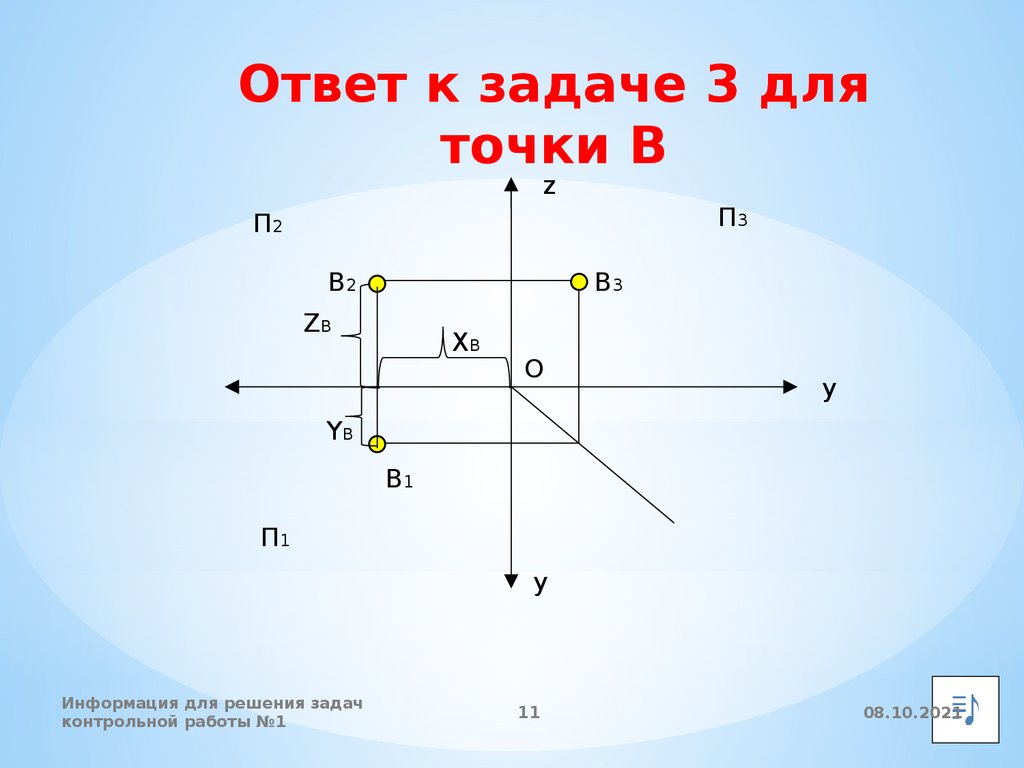
Ответ к задаче 3 для
точки В
z
П3
П2
В2
В3
ZВ
ХВ
О
y
YВ
В1
П1
y
Информация для решения задач
контрольной работы №1
11
08.10.2021

12.

Алгоритм построения следов прямой
Для построения горизонтального следа прямой необходимо:
Н
1- продолжить фронтальную проекцию прямой до
пересечения с осью Х; 2- Из точки пересечения
восстановить перпендикуляр до пересечения с
фронтальной проекцией или её продолжением.
Для построения фронтального следа прямой
нужно: 1продолжить горизонтальную проекцию прямой F
до
пересечения с осью Х; 2 - из точки пересечения
восстановить перпендикуляр до пересечения с
горизонтальной проекцией прямой
08.10.2021
Информация для решения задач
контрольной работы №1
12

13.

Построение горизонтального следа
прямой
Х
Х
Y
Y
08.10.2021
Информация для решения задач
контрольной работы №1
13

14.

z
А2
П2
А
В2
В
Ах
Х
П1
А1
Вх
В1
Н2
Н≡Н1
y
08.10.2021
O
Информация для решения задач
контрольной работы №1
Прямая пересекла
горизонтальную
плоскость проекций
в первом октанте
14

15.

Следы прямых
9. След прямой – точка пересечения прямой с
плоскостью проекций. Следы прямых (линий)
обозначаются прописными латинскими
буквами, с которых начинаются слова,
определяющие название (в латинской
транскрипции) плоскости проекций, которую
пересекает линия.
Например: H − горизонтальный след прямой
(линии) а;
F − фронтальный след прямой (линии) а;
P − профильный след прямой (линии) а.
08.10.2021
Информация для решения задач
контрольной работы №1
15

16.

След плоскости
Линия пересечения плоскости с плоскостями
проекций называется следом плоскости.
Следов всего три
Например: h0 − горизонтальный след
плоскости (поверхности);
f 0 − фронтальный след плоскости
(поверхности);
p0 − профильный след плоскости
(поверхности).
08.10.2021
Информация для решения задач
контрольной работы №1
16

17.

Пример построения проекций прямой на три
плоскости проекций и её следов
B2
П2
P≡P3
z
P2
П3
B3
A2
A3
F1
Н2
z
x
F≡F2
Н≡Н1
y
Bx
Ax
O
Ау
x
Bу
Ау
В1
П1
III,I,V
08.10.2021
Bу
y задач
Информация для решения
контрольной работы №1
Прямая АВ находится
в первом октанте.
Восходит из третьего.
Приходит в первый, затем
идёт в пятый
17

18.

Задание плоскости следами
Задание плоскости
следами обладает
преимуществом перед
другими вариантами ее
изображения на эпюре:
1) сохраняется
наглядность
изображения;
2) требуется указать
только две прямые
вместо четырех или
шести .
На рис. Показана
плоскость общего
Информация для решения задач
контрольной работы №1
положения.
08.10.2021
18

19.

Построить следы плоскости Σ (∆ АВС).
F≡F2
f0≡f2
П2
Х
Sx
В2
А2
z
С2
F'1
F1
H2
П1
Н'2 O
В1
А1
Н≡Н1
08.10.2021
F'≡F'2
Информация для решения задач
контрольной работы №1
y
С1
h0≡h1
Н≡Н'1
19

20.

Условие перпендикулярности двух прямых
• Две прямые перпендикулярны, если угол
между ними составляет 90°.
Кроме того, в начертательной геометрии
существует еще одно утверждение на эту
тему:
Две прямые перпендикулярны, если
одна из них линия уровня.
Для подтверждения этого заключения
рассмотрим примеры.
ЗАДАЧА №2
08.10.2021
Информация для решения задач
контрольной работы №1
20

21.

Пример: через точку D провести прямую ℓ, пересекающую
горизонталь h под прямым углом ℓ
h
┴
• Так как одна из сторон h прямого угла параллельна
плоскости π1, то на эту плоскость прямой угол
спроецируется без искажения. Поэтому через
горизонтальную проекцию D1 проведем горизонтальную
проекцию искомой прямой ℓ 1 h 1. Отметим
┴
горизонтальную проекцию точки пересечения прямой и
горизонтали М1= ℓ1 ∩ h1. Отметим горизонтальную
проекцию точки пересечения прямой и горизонтали М1=
ℓ1 ∩ h1. Найдем по принадлежности фронтальную
проекцию точки пересечения М2. Точки D2 и М2
определяют фронтальную проекцию искомой прямой ℓ.
Две проекции прямой определяют ее положение в
пространстве.
08.10.2021
Информация для решения задач
контрольной работы №1
21

22.

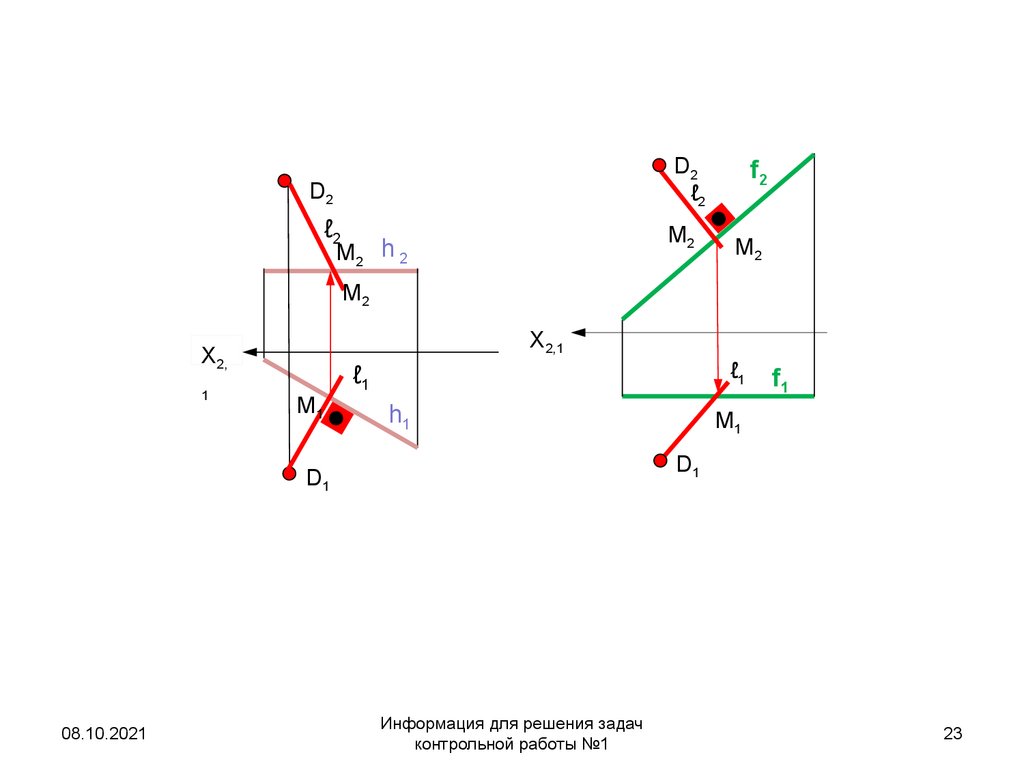
• Если вместо горизонтали будет задана ┴
фронталь f, то геометрические построения
по проведению прямой ℓ f аналогичны
рассмотренным с той лишь разницей, что
построения неискаженной проекции
прямого угла следует начинать с
фронтальной проекции (рис. б).
08.10.2021
Информация для решения задач
контрольной работы №1
22

23.

D2
ℓ2
D2
ℓ2
М2
М2 h 2
f2
М2
М2
X2,1
X2,
1
М1
ℓ1
ℓ1
h1
М1
D1
D1
08.10.2021
f1
Информация для решения задач
контрольной работы №1
23

24.

Пример. Из точки А, принадлежащей плоскости α (∆ ABC),
восставить к плоскости α перпендикуляр АD.
В2
21
D2
• Для определения
направления проекций
перпендикуляра,
проведем проекции
горизонтали h и
фронтали f плоскости ∆
ABC. После этого из точки А1
восстанавливаем
перпендикуляр к h1, а из А2
– к f2
12
h2
А2
С2
С1
D1
11
А1
08.10.2021
f2
Информация для решения задач
контрольной работы №1
h1
f1
21
В1
24

25.

• Если плоскость задана следами, для того,
чтобы прямая в пространстве была
перпендикулярна плоскости, необходимо и
достаточно, чтобы проекции этой прямой
были перпендикулярны к одноименным
следам
08.10.2021
Информация для решения задач
контрольной работы №1
25

26.

Пример. Из точки А, принадлежащей плоскости α(h0 f0) ,
восставить к плоскости α перпендикуляр АD.
D2
A2
f0
h2
12
Sx
X 2,1
h1
11
A1
h0
08.10.2021
D1
Информация для решения задач
контрольной работы №1
26

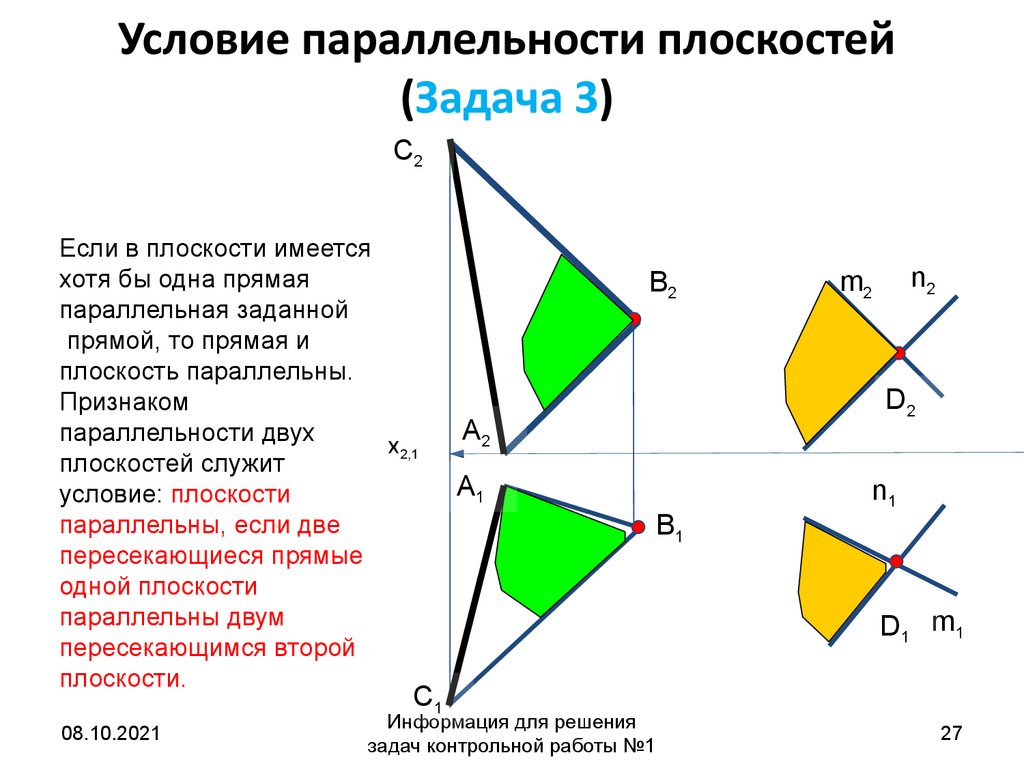
27.

Условие параллельности плоскостей
(Задача 3)
C2
Если в плоскости имеется
хотя бы одна прямая
параллельная заданной
прямой, то прямая и
плоскость параллельны.
Признаком
параллельности двух
x2,1
плоскостей служит
условие: плоскости
параллельны, если две
пересекающиеся прямые
одной плоскости
параллельны двум
пересекающимся второй
плоскости.
B2
n2
m2
D2
A2
A1
B1
n1
D 1 m1
C1
08.10.2021
Информация для решения
задач контрольной работы №1
27

28.

Линия наибольшего наклона (ската)
плоскости (лнн)
• Это линия, принадлежащая плоскости и
перпендикулярная линиям уровня (h, f, p)
этой плоскости.
• На комплексном чертеже горизонтальная
проекция (лнн)1 ┴h1, а фронтальная
проекция (лнн)2 f┴2.
• Используется эта линия для нахождения
углов наклона плоскости к плоскостям
проекций.
08.10.2021
Информация для решения
задач контрольной работы №1
28

29.

Определение расстояния между двумя точками
отрезка прямой и углов наклона отрезка способом
прямоугольного треугольника
• Натуральная величина отрезка равна гипотенузе
прямоугольного треугольника, построенного на
двух катетах один из которых проекция отрезка,
а второй – разница координат начала и конца
отрезка в другой плоскости проекций.
08.10.2021
Информация для решения
задач контрольной работы №1
29

30.

Пример определения расстояния и углов наклона
способом прямоугольного треугольника
A0
Натуральная величина
βº
∆y = yB – yA
B2
zB
A2
X2,1
∆z = zB – zA
zA
yA
A1
∆z = zB – zA
yB
A0
αº
B1
αº Угол наклона прямой к горизонтальной плоскости проекций П1
Информация для
решения проекций П2
βº Угол наклона прямой к фронтальной
плоскости
08.10.2021
задач контрольной работы №1
30

31.

Линия наибольшего наклона плоскости
АВС
к фронтальной плоскости проекций П2
f2
C2
Задача 4
12
D2
A
2
В2
Х
A1
D1
f1
В1
11
C1
08.10.2021
Информация для решения задач контрольной работы №1
DВ - линия
наибольшего
наклона
к фронтальной
плоскости
проекций
31

32.

Определить угол наклона плоскости к горизонту с
помощью линий наибольшего наклона
∆z = zB – zA
B2
Е2
A2
С2
F2
B1
h2
D2
Затем используем
правило треугольника
Е1
Задача 4
Горизонтальная
проекция лнн
перпендикулярна
горизонтальной
проекции горизонтали
С1
αº
A1
F1
08.10.2021
D1
ΔZ
h1
Информация для решения задач контрольной работы №1
32

33.

Задачи на
пересечение
Пересечение
линии с линией
l m
08.10.2021
Пересечение
линии с
поверхностью
l α
Информация для решения
задач контрольной работы №1
Пересечение
поверхности
с поверхностью
α β
33

34.

Пересечение линии с поверхностью
• Задача сводится к решению задачи на определение точки,
принадлежащей прямой и поверхности.
• Для решения необходимо:
• 1) через одну из проекций прямой провести
конкурирующую прямую, принадлежащую поверхности;
• 2) найти ее проекцию во второй плоскости проекций.
• Если эта проекция пересечет проекцию заданной прямой,
значит имеется точка пересечения прямой и поверхности.
08.10.2021
Информация для решения
задач контрольной работы №1
34

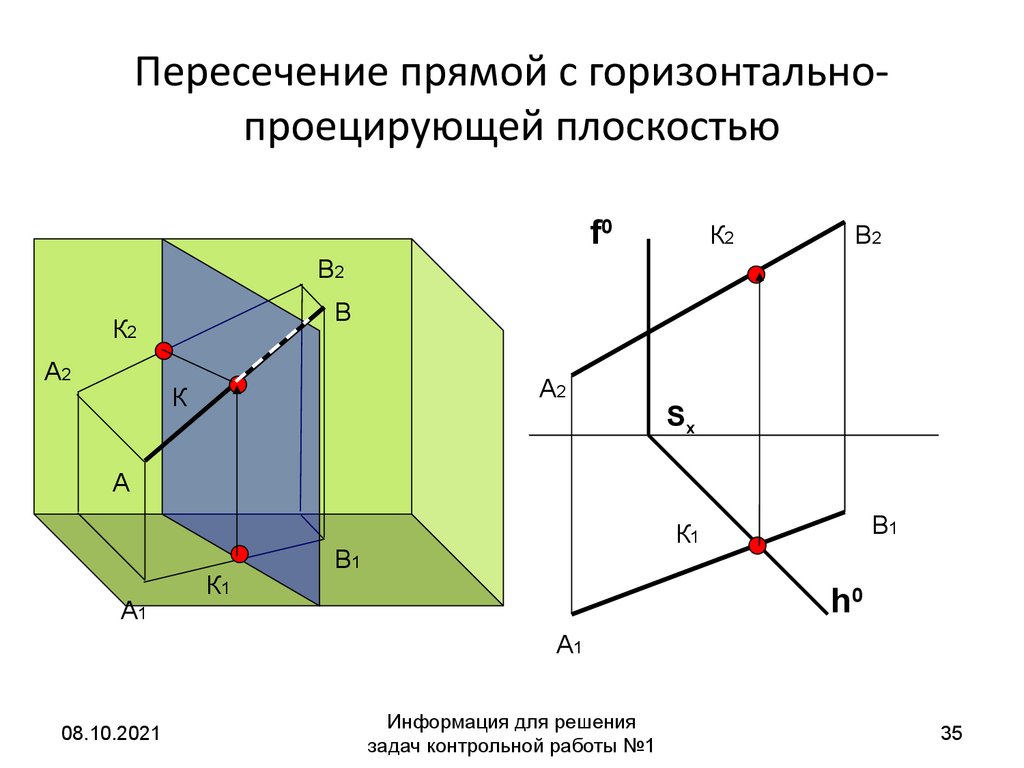
35.

Пересечение прямой с горизонтальнопроецирующей плоскостью
f0
К2
В2
В2
В
К2
А2
А2
К
Sx
А
А1
К1
В1
К1
В1
h0
А1
08.10.2021
Информация для решения
задач контрольной работы №1
35

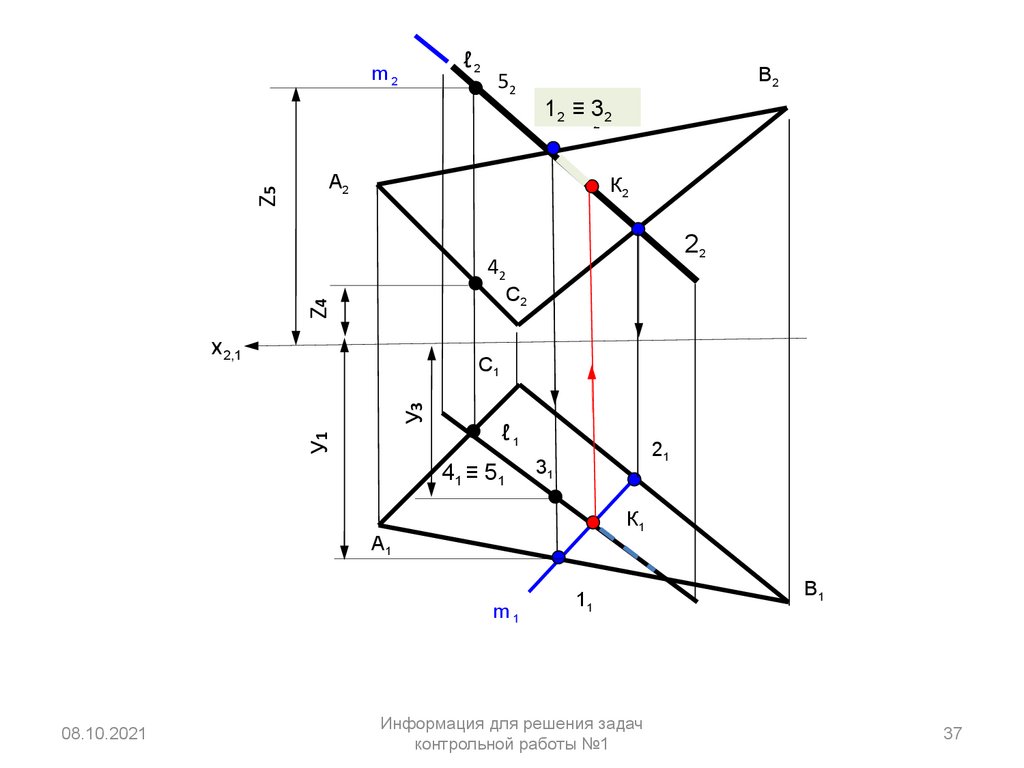
36.

Задача
Дано:
(∆ ABC), (l1,l2 )
Определить: имеется ли
точка пересечения прямой
с поверхностью α ?
ℓ2
α
B2
A2
C2
x2,1
C1
ℓ1
A1
08.10.2021
Информация для решения
задач контрольной работы №1
B1
36

37.

ℓ2
m2
52
B2
12 ≡132
Z5
2
A2
К2
Z4
42
x2,1
22
C2
У1
У3
C1
ℓ1
41 ≡ 5 1
21
31
К1
A1
m1
08.10.2021
11
Информация для решения задач
контрольной работы №1
B1
37

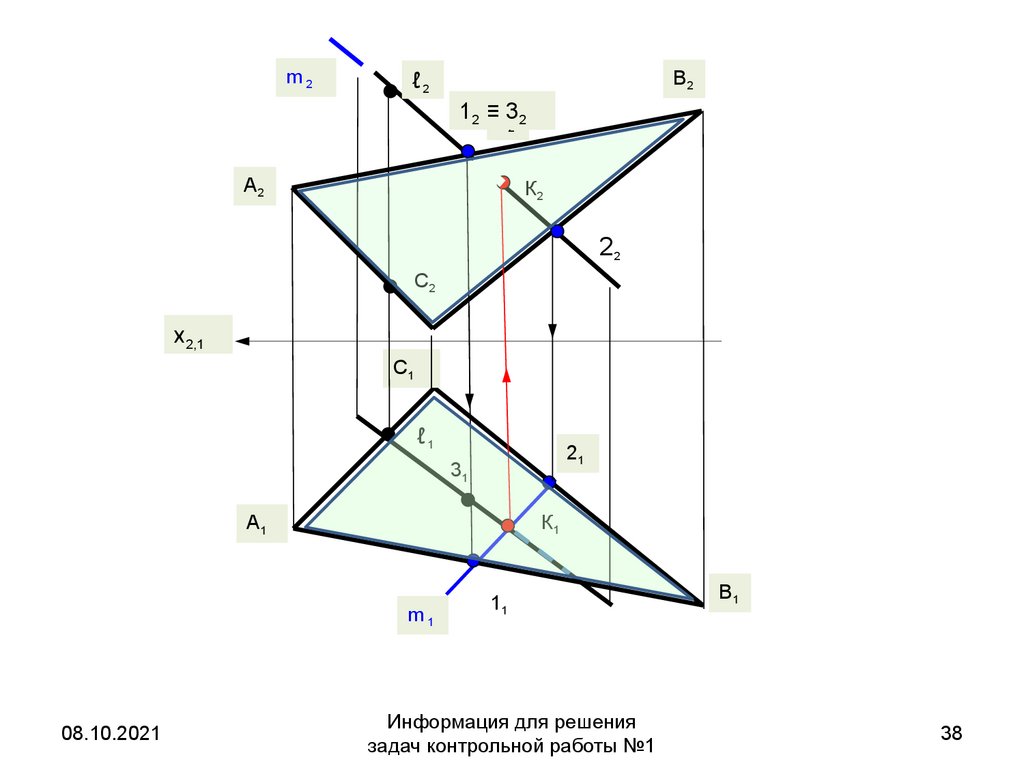
38.

m2
B2
ℓ2
12 ≡132
2
A2
К2
22
C2
x2,1
C1
ℓ1
21
31
К1
A1
m1
08.10.2021
11
Информация для решения
задач контрольной работы №1
B1
38

39.

Натуральная величина
расстояния от М до плоскости
треугольника АВС
Задача
Дано: α (∆ ABC), (М1, М2 )
Определить расстояние от
М до ∆ ABC.
1- построить линию уровня f1
М2
A2
f2
2 – опустить перпендикуляр из М
М222
М121
08.10.2021
f2
22
12
D2
C2
x2,1
A1
f1
ΔYM2
3 – для определения расстояния
применить способ прямоугольного
треугольника и использовать разницу
координат ΔYM2
проекции перпендикуляра в Π1
4 – построить гипотенузу М2D2
(расстояние от М до плоскости ∆)
прямоугольного треугольника в Π2
B2
21
11
М1
Информация для решения
задач контрольной работы №1
B1
C1
39

40.

Пересечение поверхностей
• Две поверхности пересекаются по линии, точки
которой принадлежат каждой из пересекающихся
поверхностей.
• Способ построения линии пересечения двух
поверхностей состоит в следующем: Заданные
поверхности пересекаются третьей,
вспомогательной секущей поверхностью; находят
линии, по которым эта вспомогательная
пересекает каждую из заданных поверхностей;
далее отмечаются точки в которых пересекаются
полученные линии пересечения.
08.10.2021
Информация для решения
задач контрольной работы №1
40

41.

Пересечение плоскостей
• Две плоскости
пересекаются по
прямой линии, для
определения которой
достаточно найти две
точки,
принадлежащие
одновременно
каждой из заданных
плоскостей.
08.10.2021
• Чтобы найти такие
точки достаточно
ввести две
вспомогательные
секущие плоскости.
Информация для решения
задач контрольной работы №1
41

42.

Z
B2
П1
C2
N2
D2
M2
E2
A2
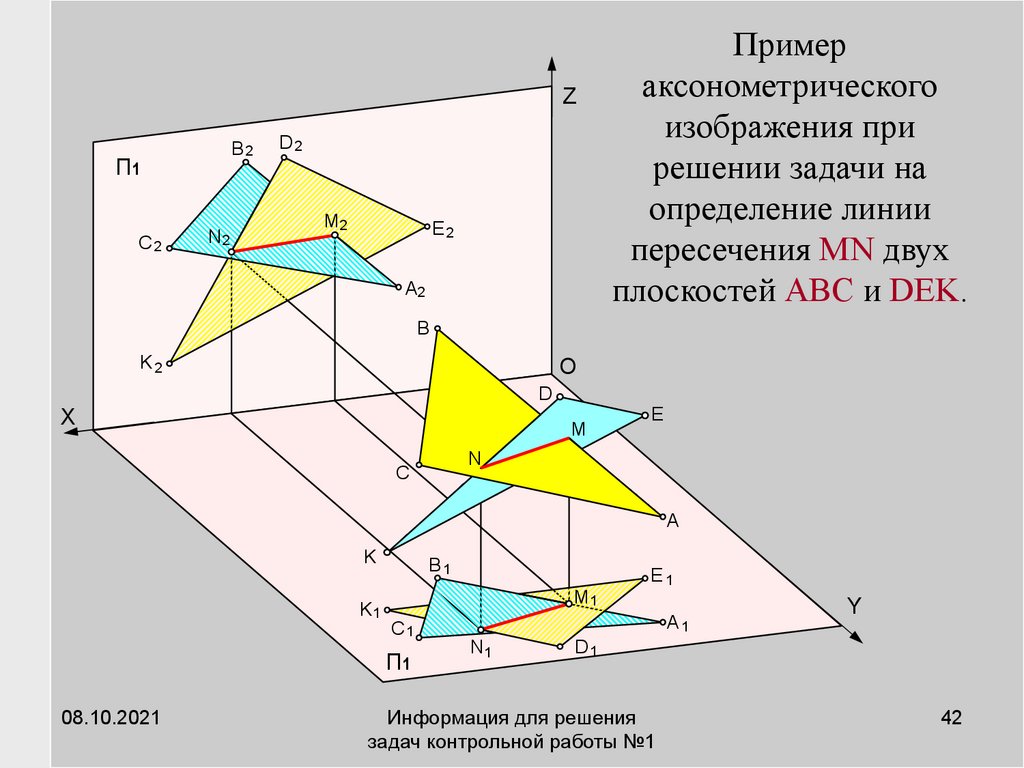
Пример
аксонометрического
изображения при
решении задачи на
определение линии
пересечения MN двух
плоскостей ABC и DEK.
B
K2
O
D
X
M
E
N
C
A
K
K1
B1
M1
C1
П1
08.10.2021
E1
A1
N1
Y
D1
Информация для решения
задач контрольной работы №1
42

43.

Дано: α (∆ ABC), β (∆ DEF);
Определить взаимное положение плоскостей
γ2
В2
E2
22 32
≡ 52
82
72
A2
42 ≡ 62
N2
F2
M2
D2
С2
21
11
08.10.2021
A1
41
51
N1
M1
D1
δ1
С1
31
7 1 ≡ 81
В1
Y6
Y3
x2,1
Y5
E1
Y4
12
61
F1
Информация для решения задач контрольной работы №1
43

44.

Пример 1. Определить линию пересечения
плоскостей
α(a b) и β(с║d)
• Алгоритм решения.
• 1. Проводим вспомогательную
горизонтально проецирующую плоскость γ
• 2. и 3. Определяем проекции прямых m и n,
по которым
пересекаются плоскости
• α(a
b) и β(с║d).
• 4. Находим точки пересечения
одноименных фронтальных проекций
линий пересечения плоскостей α и β.
08.10.2021
Информация для решения
задач контрольной работы №1
44

45.

Пример графического решения
пересечения плоскостей
a2
52
L2′
62
72
L2
22
c2
d2
32
82
42
b2
h0 ≡ h01
12
21
b1
31
L1
11
51
L1′
61
41
h0 ≡ h01 γ
81
71
γ
d1
c1
a1
08.10.2021
Информация для решения
задач контрольной работы №1
45

46.

• До свидания.
• Спасибо за внимание.
08.10.2021
Информация для решения
задач контрольной работы №1
46

47.

Информацию составил Ведякин Фёдор Филиппович
08.10.2021
Информация для решения
задач контрольной работы №1
47

48.

Возможные
варианты

49.

Вариант 1
Вопросы.
1. Что такое координаты? 2. Что такое следы плоскости?
3. Зачем нужно правило прямоугольного треугольника?
Задача. Определить расстояние от точки М до плоскости
Δ АВС.

50.

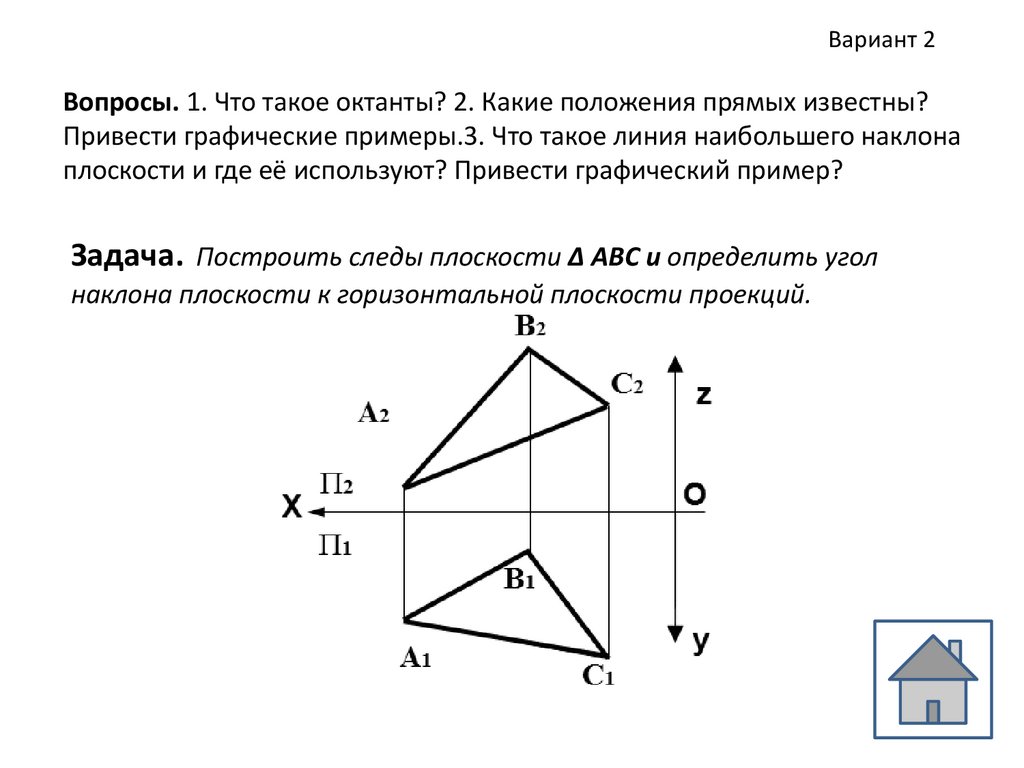
Вариант 2
Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны?
Привести графические примеры.3. Что такое линия наибольшего наклона
плоскости и где её используют? Привести графический пример?
Задача. Построить следы плоскости Δ АВС и определить угол
наклона плоскости к горизонтальной плоскости проекций.

51.

Вариант 3
Вопросы. Что такое координаты? 2. Что такое следы прямых, их
обозначение и назначение? Их графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
Задача. Определить взаимное положение плоскости Σ(Δ АВС) с
прямой общего положения ℓ и угол наклона прямой к горизонтальной
плоскости проекций.

52.

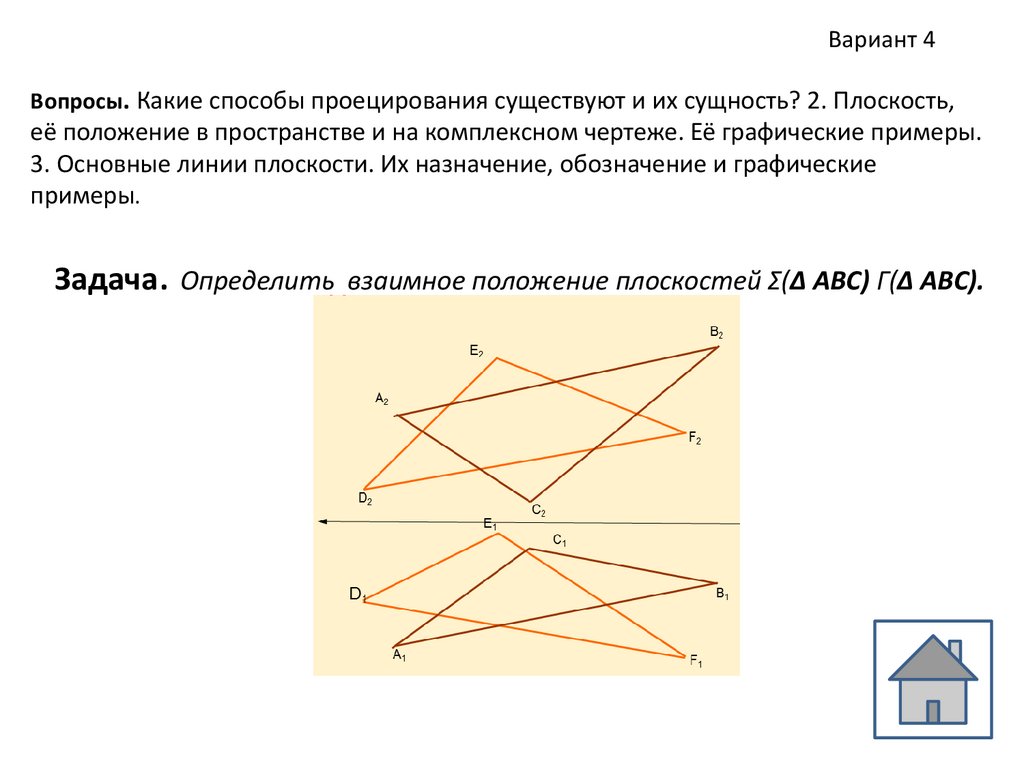
Вариант 4
Вопросы. Какие способы проецирования существуют и их сущность? 2. Плоскость,
её положение в пространстве и на комплексном чертеже. Её графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
Задача. Определить взаимное положение плоскостей Σ(Δ АВС) Г(Δ АВС).

53.

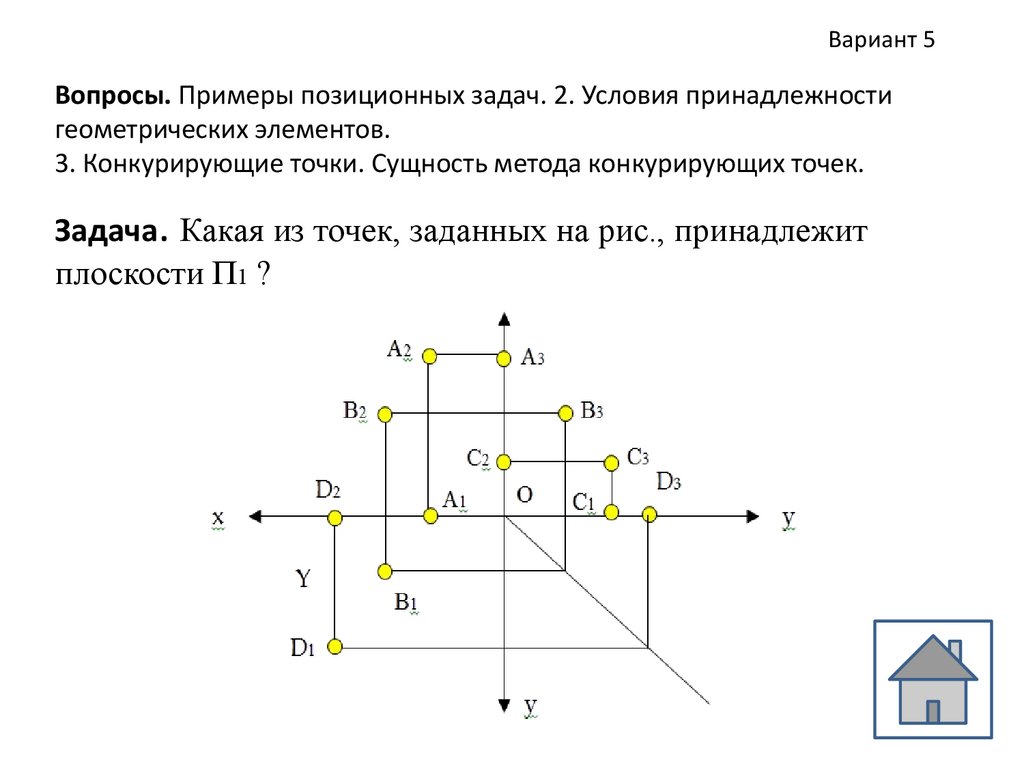
Вариант 5
Вопросы. Примеры позиционных задач. 2. Условия принадлежности
геометрических элементов.
3. Конкурирующие точки. Сущность метода конкурирующих точек.
Задача. Какая из точек, заданных на рис., принадлежит
плоскости П1 ?

54.

Вариант 6
Вопросы. Условия принадлежности геометрических элементов? 2. Прямая, её
положение в пространстве и на комплексном чертеже. Графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
ЗАДАЧА. Для создания комплексного чертежа для точки А, по её
координатам (45, 36,25 ) построить три её проекции:

55.

Вариант 7
Вопросы.
1. Что такое координаты? 2. Что такое следы плоскости?
3. Зачем нужно правило прямоугольного треугольника?
Задача. Определить расстояние от точки М до плоскости
Δ АВС.

56.

Вариант 8
Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны?
Привести графические примеры.3. Что такое линия наибольшего наклона
плоскости и где её используют? Привести графический пример?
Задача. Построить следы плоскости Δ АВС и определить угол
наклона плоскости к горизонтальной плоскости проекций.

57.

Вариант 9
Вопросы. Что такое координаты? 2. Что такое следы прямых, их
обозначение и назначение? Их графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
Задача. Определить взаимное положение плоскости Σ(Δ АВС) с
прямой общего положения ℓ и угол наклона прямой к горизонтальной
плоскости проекций.

58.

Вариант 10
Вопросы. Какие способы проецирования существуют и их сущность? 2. Плоскость,
её положение в пространстве и на комплексном чертеже. Её графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
Задача. Определить взаимное положение плоскостей Σ(Δ АВС) Г(Δ АВС).

59.

Вариант 11
Вопросы. Примеры позиционных задач. 2. Условия принадлежности
геометрических элементов.
3. Конкурирующие точки. Сущность метода конкурирующих точек.
Задача. Какая из точек, заданных на рис., принадлежит
плоскости П1 ?

60.

Вариант 12
Вопросы. Условия принадлежности геометрических элементов? 2. Прямая, её
положение в пространстве и на комплексном чертеже. Графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
Для создания комплексного чертежа для точки А,
по её координатам (45, 36,25 ) построить три её проекции
ЗАДАЧА.