Similar presentations:
Понятие производной
1.
Производная2.
Понятие производнойПроизводной функции у = f(x), заданной на некотором
интервале (a; b), в некоторой точке х этого
интервала называют предел отношения приращения
функции в этой точке к соответствующему
приращению
аргумента,
когда
приращение
аргумента стремится к нулю.
∆f
f ′(x) = lim
∆x→0 ∆x
Нахождение производной называют дифференцированием
3.
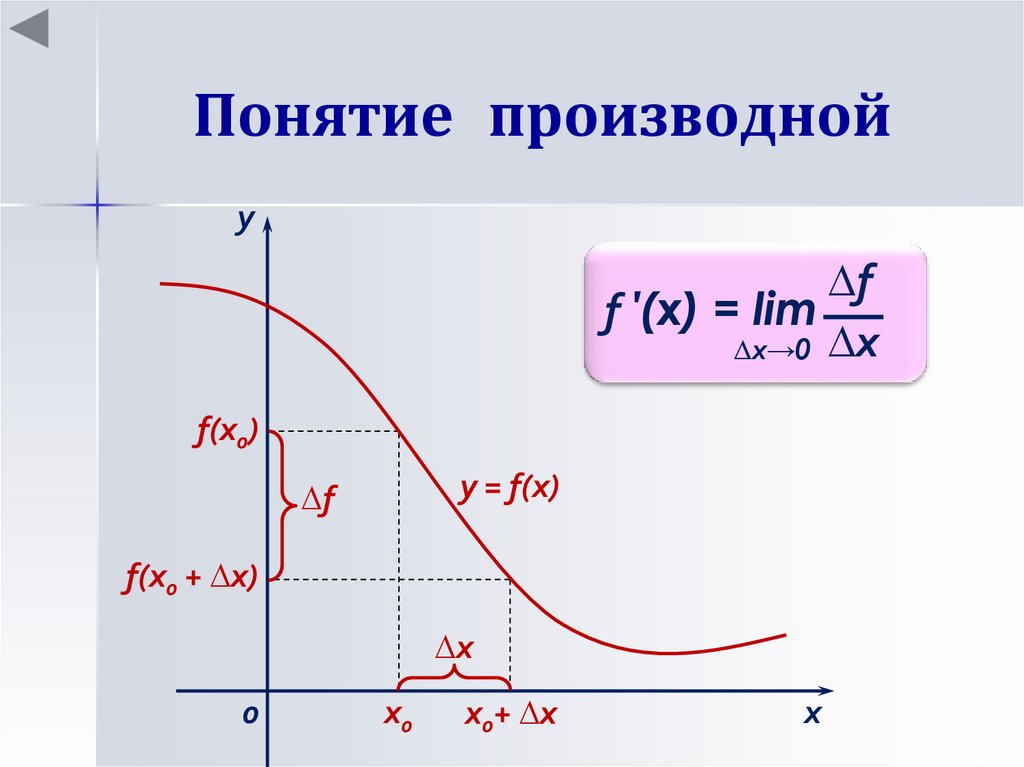
Понятие производнойу
∆f
f ′(x) = lim
∆x→0 ∆x
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х
4.
Алгоритм нахожденияпроизводной
1. Зафиксировать значение х0, найти f(x0).
2. Дать аргументу х0 приращение ∆х, перейти в
новую точку х0 + ∆х, найти f(x0 + ∆х).
3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0).
∆f
4. Составить отношение
.
∆х
∆f
5. Вычислить lim
.
∆x→0 ∆х
6. Этот предел и есть f ′(x0).
5.
Примеры1. Найти производную функции y = kx + b в точке хo
1. f xo kxo b
2. f xo Δx k xo Δx b
3. Δf f x o Δx f x o k x o Δx b kxo b
kxo k Δx b kxo b k Δx
Δf
k Δx
4.
k
Δx
Δx
Δf
5. lim
lim k k
Δx 0 Δx
Δx 0
kx b
k
6.
Примеры2. Найти производную функции y = C (C – const) в точке хo
1. f xo С
2. f xo Δx С
3. Δf f xo Δx f xo С С 0
Δf
0
4.
0
Δx Δx
Δf
5. lim
lim 0 0
Δx 0 Δ x
Δx 0
С 0
7.
Примеры3. Найти производную функции y = x2 в точке хo
1. f xo xо
2
2. f xo Δx xo Δx
2
3. Δf f x o Δx f x o x o Δx x o
2
2
x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2
2x o Δx Δx 2 Δx 2 x o Δx
Δf
4.
2 x o Δx
Δx
Δx
Δx
Δf
5. lim
lim 2 x o Δx 2 x o
Δx 0 Δ x
Δx 0
x 2х
2
8.
Примеры4. Найти производную функции y = √x в точке хo
1. f x o x o
2. f xo Δx xo Δx
3. Δf f xo Δx f x o x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
x o Δx x o
Δf
4.
Δx Δx
x o Δx
x
2
o
x o Δx x o
Δx
x o Δx x o
Δx
x o Δx x o
2
1
x o Δx x o
9.
Примеры4. Найти производную функции y = √x в точке хo
Δf
4.
Δx Δx
Δx
x o Δx x o
1
x o Δx x o
Δf
1
1
5. lim
lim
2 x
Δx 0 Δx
Δx 0 x Δx
x
o
o
o
x
1
2 х
10.
Примеры5. Найти производную функции y = 1/x в точке хo
1
1. f x o
xо
1
2. f x o Δx
x o Δx
1
1
3. Δf f x o Δx f x o
x o Δx x o
x o x o Δx
Δx
2
x o x o Δx
x о x o Δx
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
11.
Примеры5. Найти производную функции y = 1/x в точке хo
Δf
Δx
1
4.
2
2
Δx Δx x о x o Δx
x о x o Δx
Δf
1
1
2
5. lim
lim 2
Δx 0 Δx
Δx 0 x x Δx
xо
o
о
1
1
2
х
х
12.
Физический ( механический) смысл производной
Если при прямолинейном движении путь s,
пройденный точкой, есть функция от времени t,
т.е. s = s(t), то скорость точки есть производная
от пути по времени, т.е. v(t) = s′(t).
Производная выражает мгновенную скорость в
момент времени t.
13.
Если функция имеет производную (дифференцируема)в точке х, то она непрерывна в этой точке.
14.
Прочитайте п.4.1, обратитевнимание на понятия выделенные в
розовых рамках Стр92,94..
Рассмотрите примеры в учебнике и
в презентации.
Попробуйте выполнить №4.1 и 4.3.
15.
После дистанта нам нужно написатьконтрольную. Вводную диагностику.
И приступим к изучению производной.














 mathematics
mathematics








