Similar presentations:
Властивості задачі лінійного програмування
1.
Властивості задачілінійного
програмування
2.
Властивості задачі лінійногопрограмування
3.1 Форми ЗЛП
3.2 Еквівалентність форм ЗЛП
3.3 Множина допустимих розв’язків ЗЛП (багатогранні множини,
багатогранники, вершини, грані)
3.4 Основні властивості ЗЛП і теореми лінійного програмування
3.
3.3 Множина допустимих розв’язків ЗЛП(багатогранні множини, багатогранники,
вершини, грані)
4.
Гіперплощинаn
Визначення. Множина точок простору R , координати яких
задовольняють рівнянню
a1x1 a2 x2 an xn b ,
a1
де a j R, a ... 0, b R , називається гіперплощиною H ab
an
.
Короткий запис визначення:
H ab = x R n aT x b .
5.
НапівпросториВизначення. Множини
x R
a x b ,
H ab
x R n aT x b ,
H ab
n
що породжуються гіперплощиною
(закритими) напівпросторами.
T
H ab , називаються
6.
НапівпросториВідкриті ніпівпростори:
H ab
x R n aT x b
H ab
x R
n
a x b
T
7.
НормальВизначення.
Вектор a називається нормаллю до гіперплощини
H ab .
.
Нормаль ортогональна до H ab і направлена у бік простору H ab
8.
Твердження. ГіперплощинаH ab є опуклою множиною.
Твердження Перетин довільного числа опуклих множин також є
опуклою множиною.
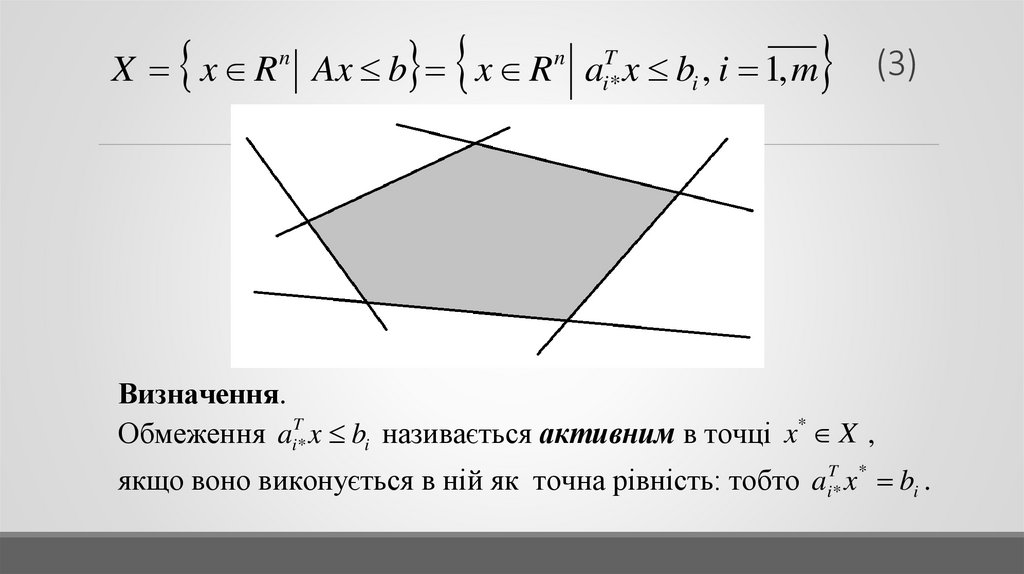
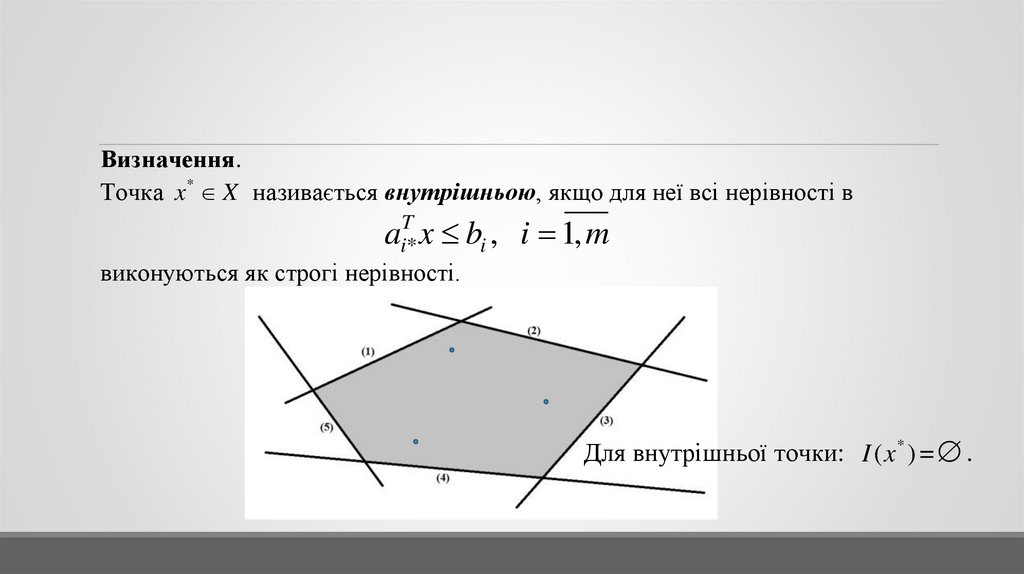
Визначення. Множина, утворена перетином скінченого числа
напівпросторів і гіперплощини (якщо цей перетин не порожній)
називається багатогранною множиною.
Визначення. Багатогранником називається обмежена
багатогранна множина.











































 programming
programming








