Similar presentations:
Геометрия. Построение
1.
Вопросы для устногоповторения
Дайте определение трапеции;
Как называются стороны трапеции?
Какие виды трапеций существуют?
Перечислите свойства равнобедренной
трапеции;
2.
Задачи на построениеУчебная презентация
по геометрии
для 8 класса
3.
В геометрии специально выделяютзадачи на построение, которые
решаются только с помощью двух
инструментов: ЦИРКУЛЯ И ЛИНЕЙКИ
без масштабных делений.
4.
Основные этапы решениязадач на построение
1.
2.
3.
4.
Анализ;
Построение;
Доказательство;
Исследование
В том случае, когда при построении получаются
равные фигуры, будем считать, что задача имеет
единственное решение
5.
Что делают на каждом этапе?1. Анализ: допустим, что фигура построена, рисуют эскиз
фигуры и устанавливают связи между данными задачи и
искомыми элементами, намечают план построения
искомой фигуры;
2. Построение: при помощи циркуля и линейки без
масштабных делений выполняют последовательное
выполнение простейших построений;
3. Доказательство: обоснование того, что построенная
фигура удовлетворяет условиям задачи;
4. Исследование: ответ на вопрос, при любых ли данных
задача имеет решение, и, если имеет, то сколько
6.
Простейшие построения1.
2.
3.
4.
5.
Отложить отрезок, равный данному;
Построить угол, равный данному;
Построить биссектрису данного угла;
Построить перпендикулярные прямые;
Построить середину отрезка
7.
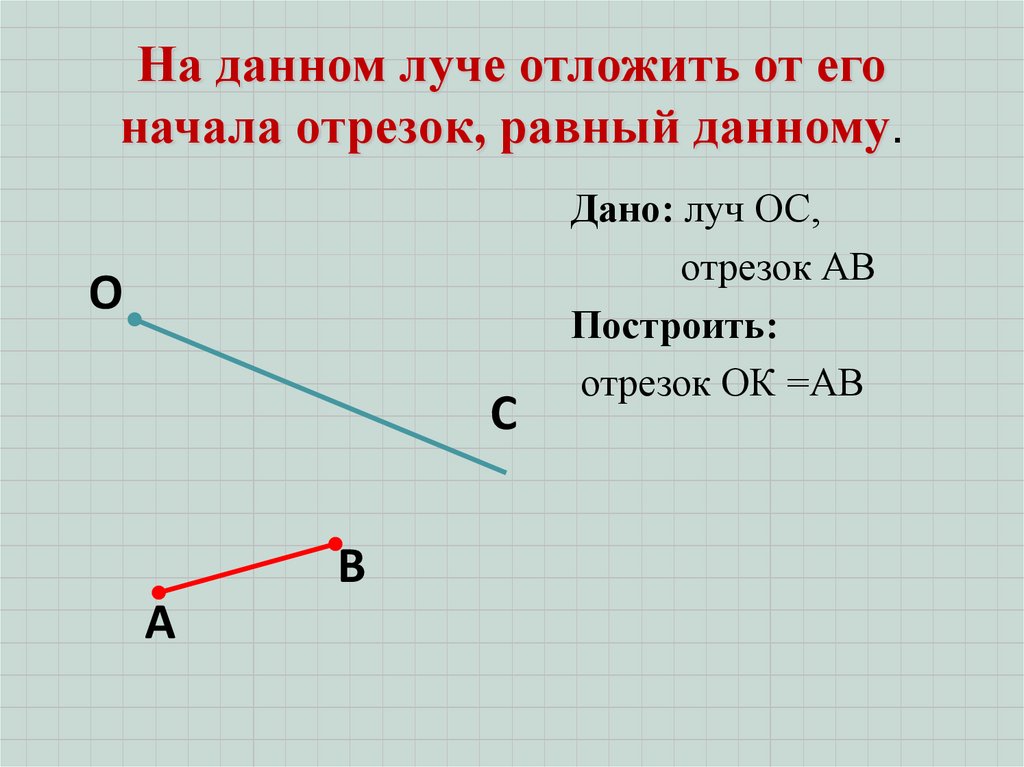
На данном луче отложить от егоначала отрезок, равный данному.
О
С
В
А
Дано: луч ОС,
отрезок АВ
Построить:
отрезок ОК =АВ
8.
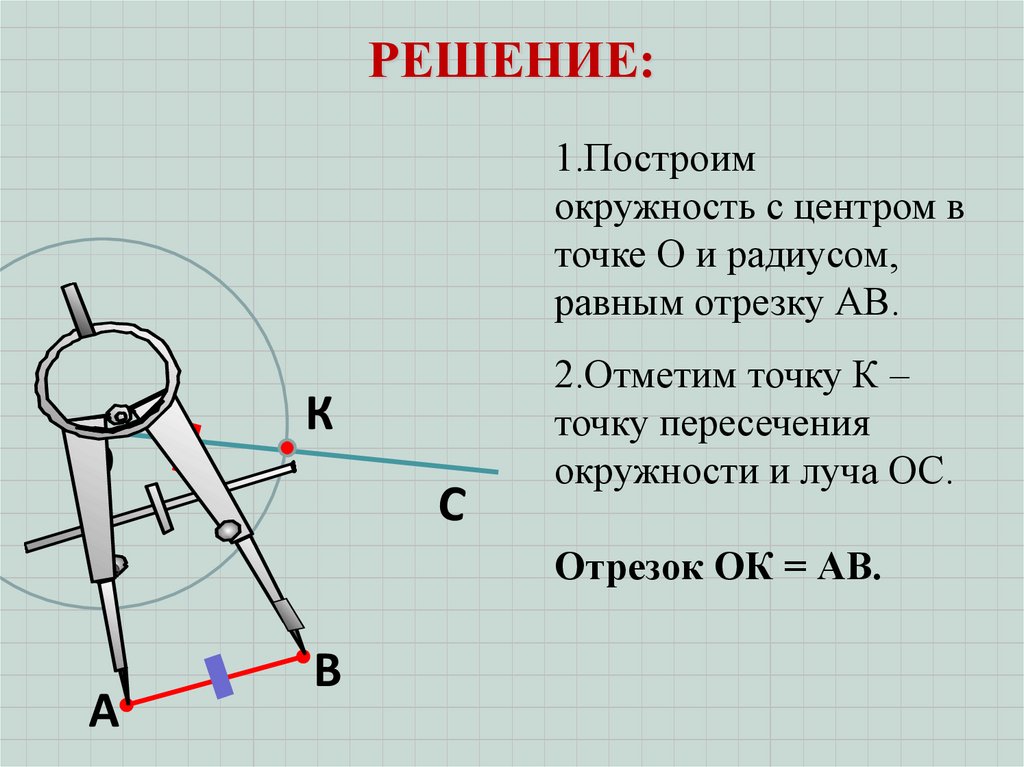
РЕШЕНИЕ:1.Построим
окружность с центром в
точке О и радиусом,
равным отрезку АВ.
О
К
2.Отметим точку К –
точку пересечения
окружности и луча ОС.
Отрезок ОК = АВ.
А
В
9.
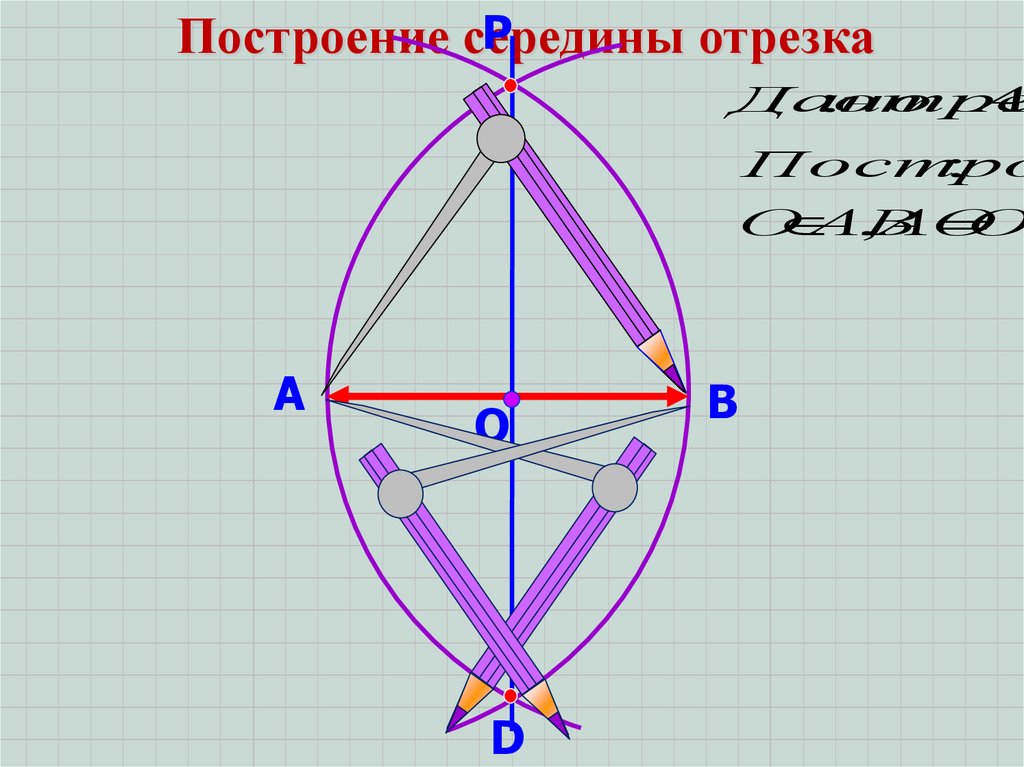
PПостроение середины
отрезка
Дано
:отре
А
Постро
:
О
АВ
,АО
О
А
О
D
В
10.
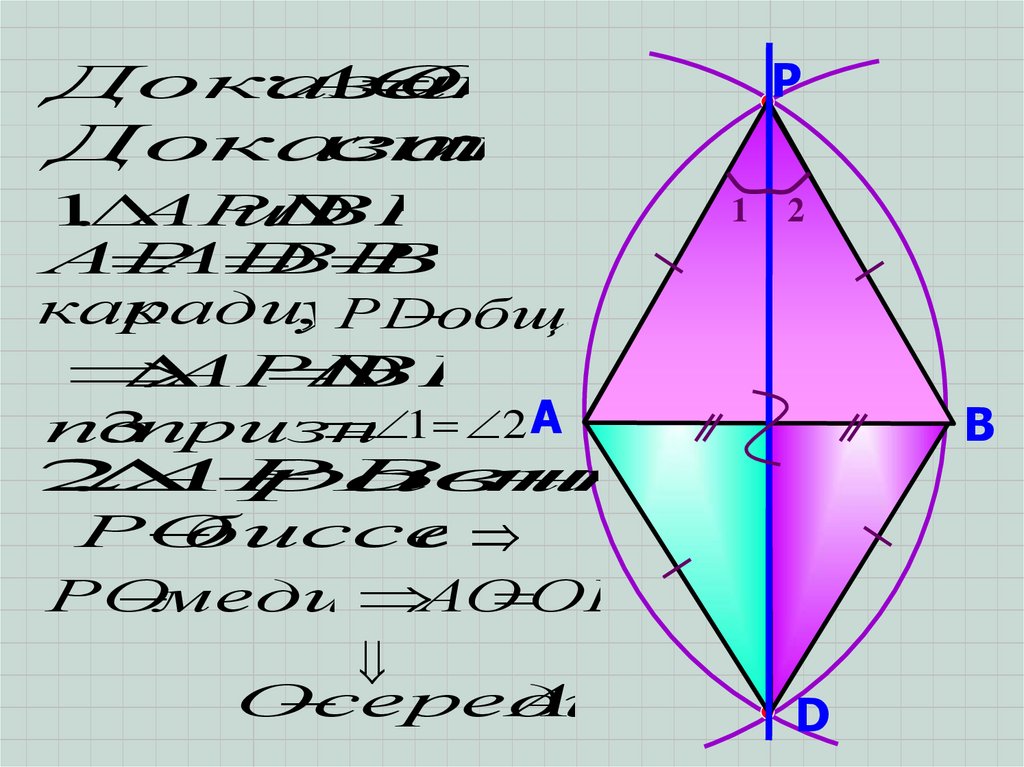
Доказать:АО
ОВ
P
Доказатель
ство
:
1 2
1
.
АPD
и
BPD
АP
АD
ВР
BD
как
радиусы
, РD
общая
АPD
BPD
1 2 А
В
по
3признаку
О
2
.
АРВ
равнобедр
нный
РО
биссектрис
а
РО
медиана
АО
ОВ
О
середина
АВ
D
11.
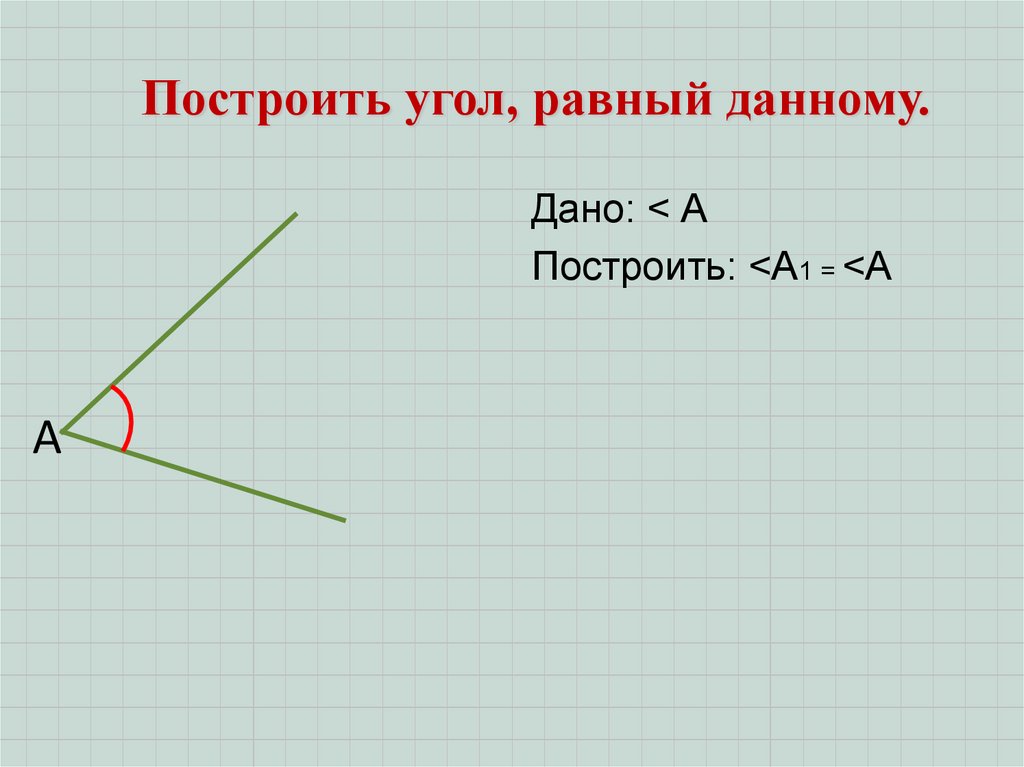
Построить угол, равный данному.Дано: < А
Построить: <А1 = <А
А
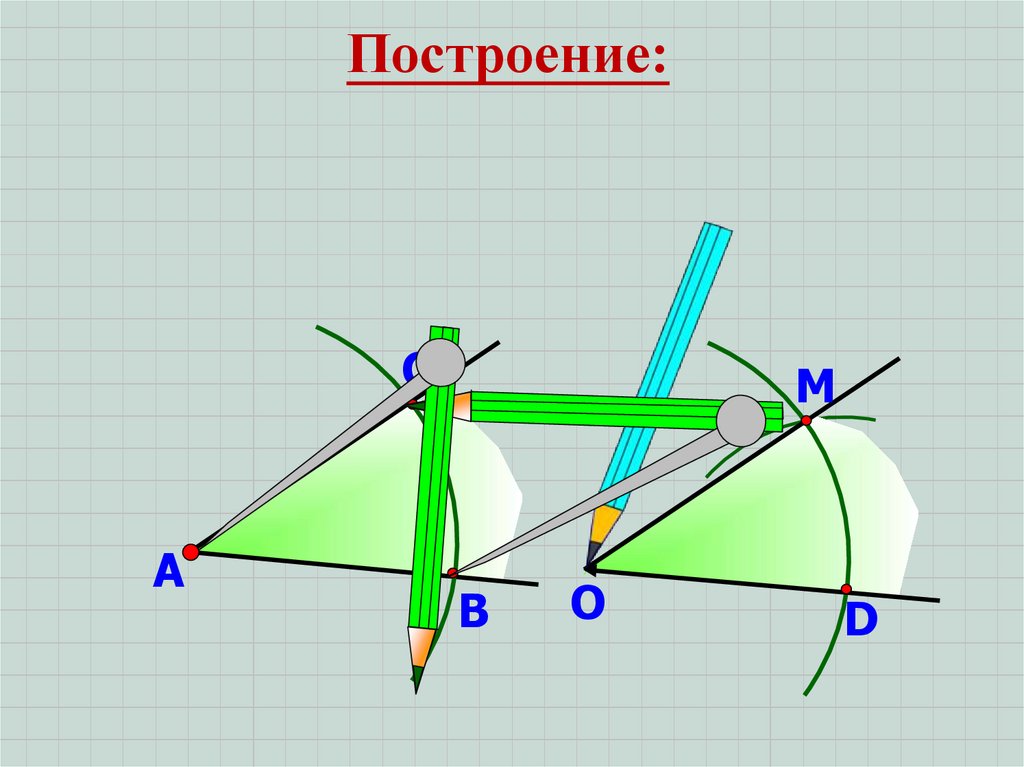
12.
Построение:С
А
М
В
О
D
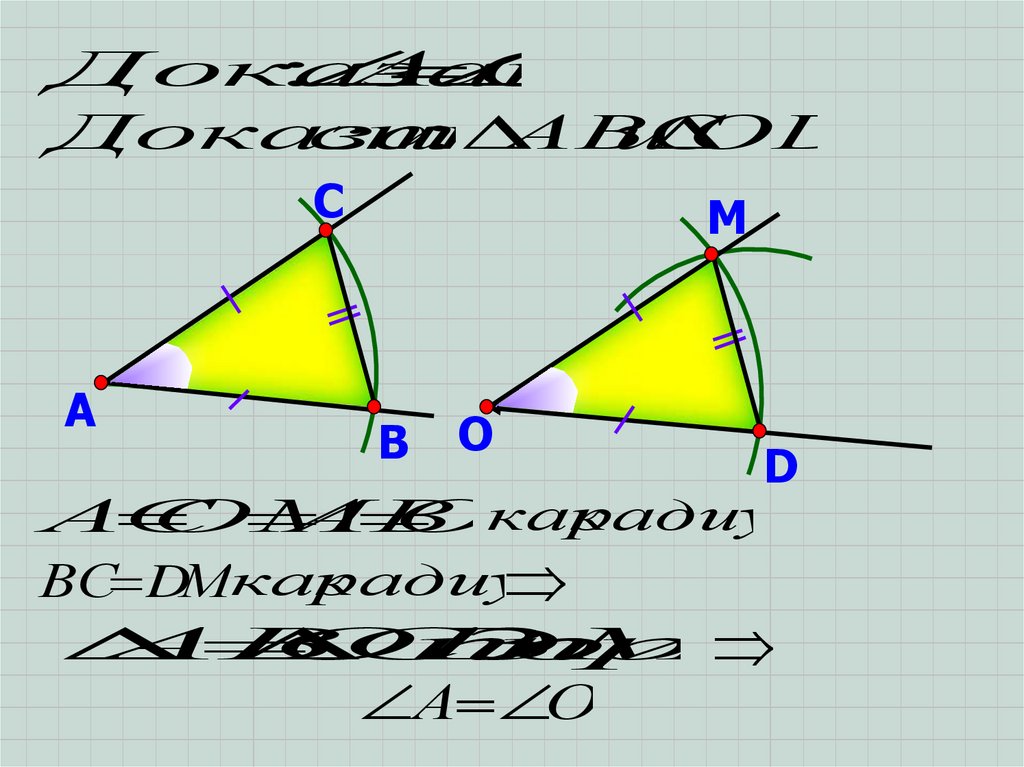
13.
Доказать:
А
О
АВС
и
ОDМ
Доказатель
ство
:
С
А
М
В
О
D
как
радиусы
АС
ОМ
АВ
ОD
радиусы
ВС DМкак
АВС
ОDМ
по
3
призна
А О
14.
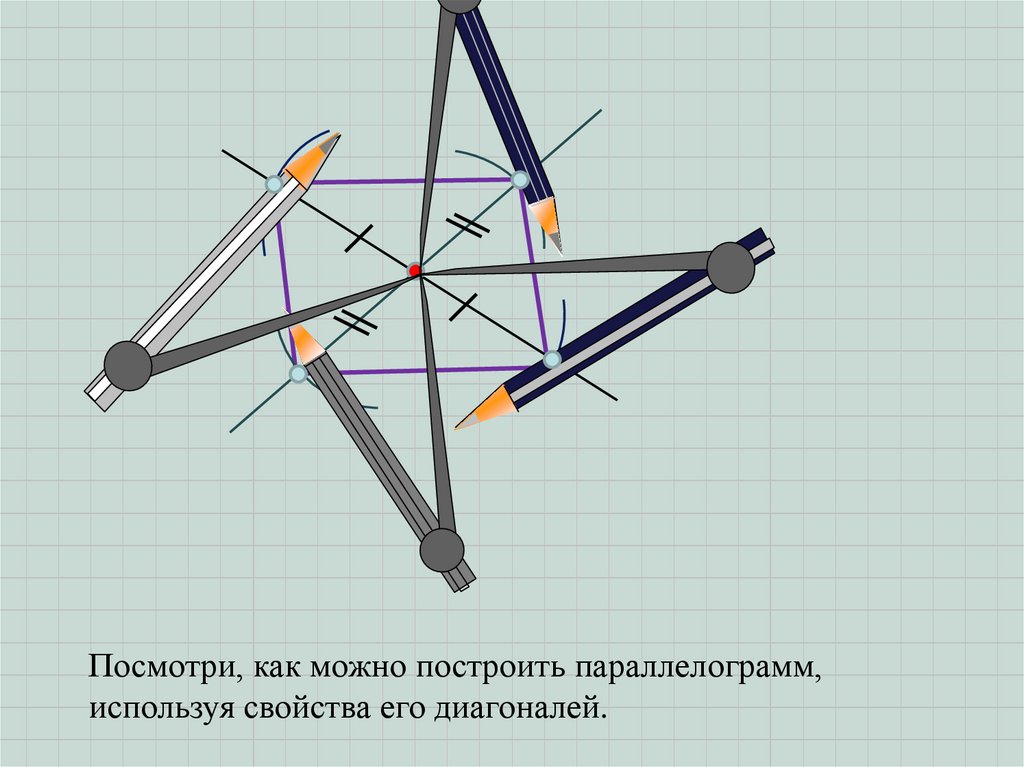
Посмотри, как можно построить параллелограмм,используя свойства его диагоналей.
15.
№ 39416.
Задача № 397 (а)17.
Домашнее заданиеРешить задачи № 395, 396, 398









 mathematics
mathematics








