Similar presentations:
Задачи на построение
1.
2.
В геометрии выделяют задачи на построение,которые можно решить только с помощью двух
инструментов:
1) циркуля
с помощью
которого
можно провести окружность произвольного
радиуса, а также окружность с центром в данной
точке и радиусом, равным данному отрезку;
2) линейки без масштабных делений,
которая позволяет провести произвольную
прямую, а также построить прямую,
проходящую через две данные точки.
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.
Простейшие задачи на построениеВ
А
О
О
О
b
b
М
М
а
а
4.
P 1.Построение : Задача
Построение середины отрезка.
Дано : отрезок АВ
Построить :О АВ, АО ОВ
А
В
О
D
5.
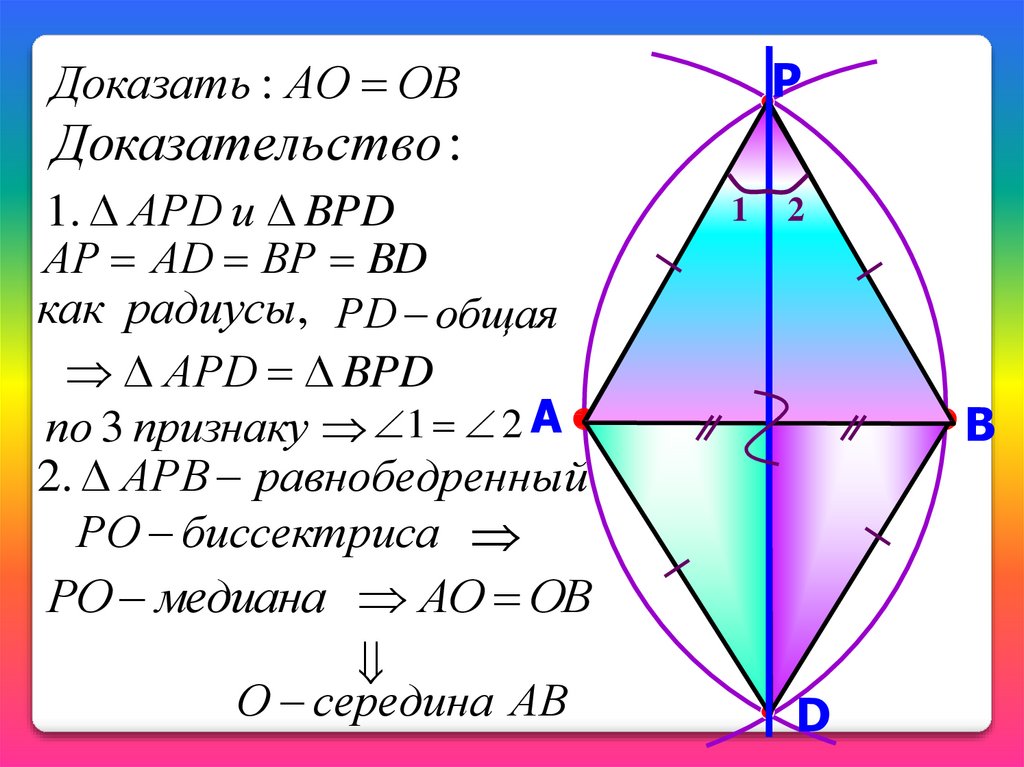
Доказать : АО ОВP
Доказательство :
1. АPD и BPD
АP АD ВР BD
как радиусы, РD общая
АPD BPD
по 3 признаку 1 2 А
2. АРВ равнобедренный
РО биссектриса
РО медиана АО ОВ
О середина АВ
1
2
В
О
D
6.
2.ПостроениеЗадача
:
Построение угла, равного данному.
Дано : А
Построить: О А
С
А
М
В
О
D
7.
Доказать : А ОДоказательство : АВС и ОDМ
С
А
М
В
О
АС ОМ АВ ОD как радиусы
ВС DМ как радиусы
АВС ОDМ по 3 признаку
А О
D
8.
3.ПостроениеЗадача
:
Построение биссектрисы угла.
Дано : А
Построить : биссектрису А
С
А
D
В
9.
Доказать : АD биссектриса АДоказательство : АВD и АCD
АС СD АB ВD как радиусы
АD общая АВD АCD по 3 признаку
1 2 АD биссектриса А
С
D
1
А
2
B
10.
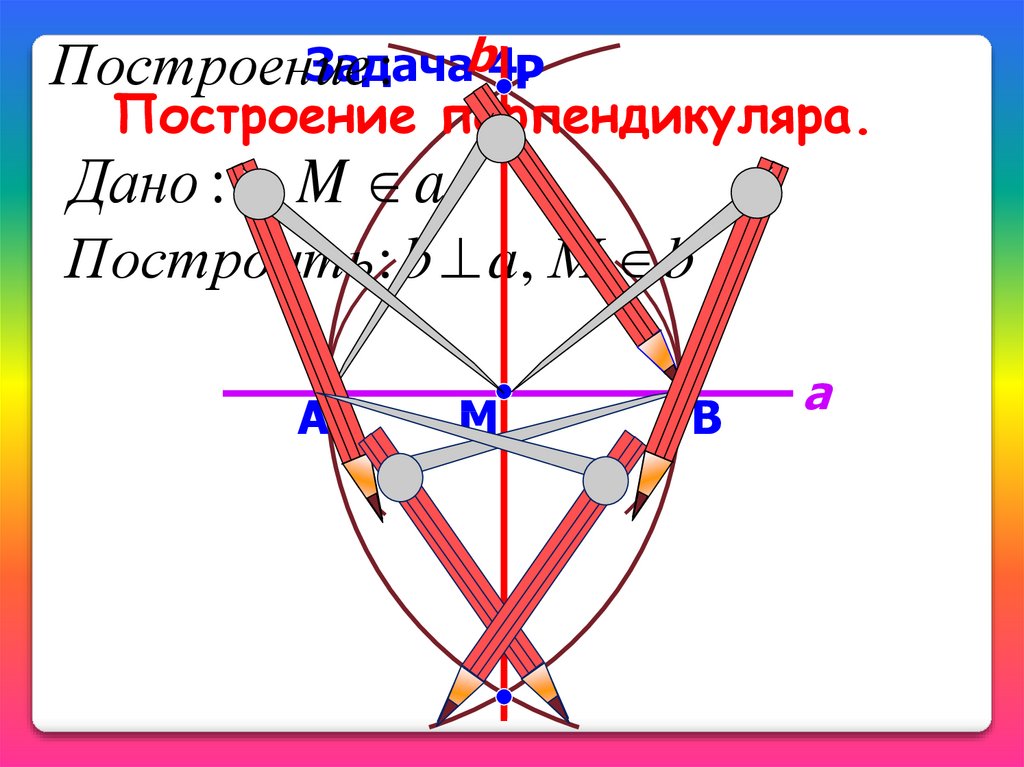
ЗадачаПостроение
: b4.Р
Построение перпендикуляра.
Дано : a, M a
Построить : b a, М b
А
M
В
a
11.
Доказать : a bДоказательство :
АРВ : АР РВ
как радиусы
АРВ
равнобедренный;
А
АМ МВ
как радиусы
РМ медиана
РМ высота
РМ АВ или b a
b Р
M
В a
12.
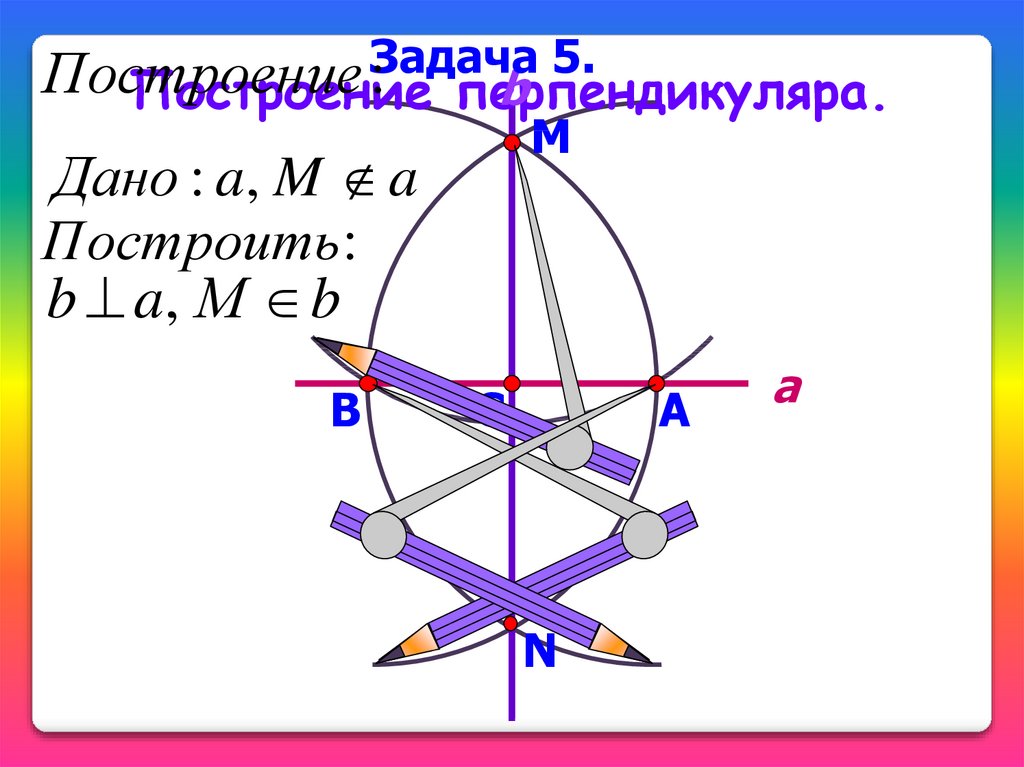
Задача 5.Построение
:
b
Построение перпендикуляра.
М
Дано : a, M a
Построить:
b a, М b
B
C
A
N
a
13.
Доказать : a bДоказательство :
1. MBN и MAN
АМ AN ВМ ВN
b
М
1
2
как радиусы
MN общая
B
C
MBN MAN
по 3 признаку 1 2
2. АМВ равнобедренный
МС биссектриса
МС высота
N
МС АВ или b a
A
a










 mathematics
mathematics








