Similar presentations:
Кинематика материальной точки
1. Кинематика материальной точки
КИНЕМАТИКА МАТЕРИАЛЬНОЙТОЧКИ
2.
Кинематика изучает движение тел, нерассматривая причины, которые это
движение оуславливают
3.
ПОСТУПАТЕЛЬНОЕПоступательное
ДВИЖЕНИЕ
движение
–
это
движение, при котором любая прямая,
жестко связанная с телом, остается
параллельной своему первоначальному
положению
4. Скорость
СКОРОСТЬСкорость
– это векторная величина, которая
определяет
как
быстроту
движения
материальной точки, так и ее направление в
данный момент времени.
Под
средней скоростью движения по
траектории за конечное время t понимают
отношение пройденного за это время
конечного пути S ко времени
S S 2 S1
vs
t
t 2 t1
5.
Средняя скорость перемещения точки — величина,направленная вдоль вектора перемещения.
r r2 r1
vr
t t 2 t1
S
v lim
t 0 t
Производная радиус-вектора r по времени
определяет мгновенную скорость
перемещения точки.
dr
v
dt
dS dr
v
dt dt
6.
Если модуль скорости увеличивается стечением времени, то движение
называется ускоренным, если же он
убывает с течением времени, то
движение называется замедленным.
7. Ускорение
УСКОРЕНИЕУскорение – это векторная величина,
характеризующая быстроту изменения
скорости по модулю и направлению.
v dv
a lim
v r
t 0 t
dt
a ax i a y j az k x i y j z k
a a x2 a 2y a z2
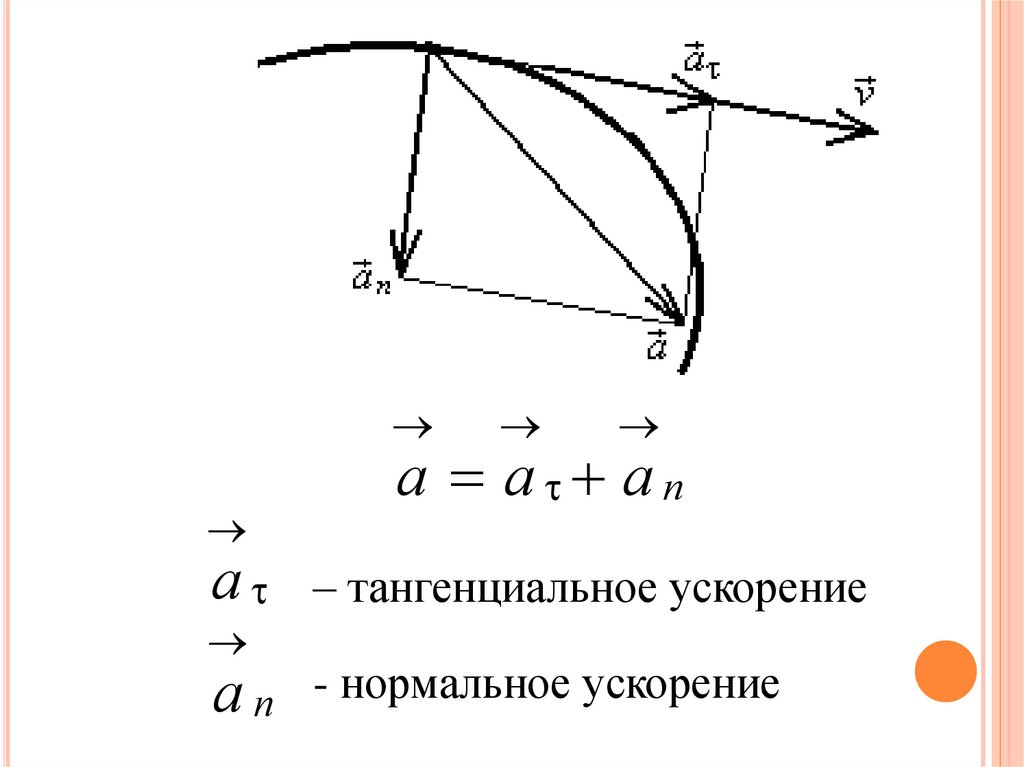
8.
aan
a a an
– тангенциальное ускорение
- нормальное ускорение
9.
Как видно из этого рисунка, модуль общегоускорения равен:
2
2
a a a
Рассмотрим
несколько
(частных) случаев:
a 0; a 0
n
a const; a
n
n
предельных
– равномерное прямолинейное движение;
0
– равноускоренное
прямолинейное движение;
a 0; a const – равномерное движение
n
по окружности.
10.
dva
dt
тангенциальное ускорение при
криволинейном движении.
v n
v1 s v 2
a n lim
lim
t 0 t
t 0 R t
R
2
v
an
R
нормальное
ускорение при
криволинейном
движении
11.
•Равномерное движение материальнойточки по окружности: v = const.
• Тогда тангенциальное ускорение равно
нулю и полное ускорение равно
нормальному, т.е. центростремительному
ускорению:
dv
a
0
dt
2
v
a an
R
12.
•Прямолинейное движение материальной точки:В этом случае радиус кривизны траектории равен
бесконечности и нормальное ускорение равно
нулю. Полное ускорение равно тангенциальному
и направлено вдоль направления движения: если
а 0, по направлению движения, если а 0,
против направления движения.
2
v
R an
0
R
dv
a a
dt
13. Вращательное движение вокруг неподвижной оси
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ВОКРУГНЕПОДВИЖНОЙ ОСИ
Вращательное движение – это такое
движение, при котором все точки тела
движутся по окружностям, центры
которых лежат на одной и той же прямой,
называемой осью вращения.
Ось вращения может находиться и вне
тела.
14.
Пусть абсолютно твердоетело вращается вокруг
неподвижной оси ОО'
Проследим за некоторой
точкой М этого твердого
тела. За время dt точка
М совершает
элементарное
перемещение
15.
Угол поворота dφ характеризуетперемещения всего тела за время dt
(угловой путь)
Угловое перемещение вектор, численно
равный углу поворота тела за время и
направленный вдоль оси вращения так, что, глядя
вдоль
него,
поворот
тела
наблюдается
происходящим по часовой стрелке.
16.
Удобно ввести dφ – векторэлементарного поворота тела, численно
равный dφ и направленный вдоль оси
вращения ОО' так, чтобы вдоль вектора
мы видели вращение по часовой стрелке
(направление вектора dφ и
направление вращения связаны
правилом буравчика).
17.
Элементарные повороты удовлетворяютобычному правилу сложения векторов:
dφ dφ dφ .
1
2
Угловой скоростью ω
называется вектор
численно равный первой производной от угла
поворота по времени и направленный
вдоль
оси вращения в направлении dφ ( ω и dφ
всегда направлены в одну сторону).
dφ
ω
dt
dφ
ω .
dt
18.
Связь линейной и угловой скоростиПусть – линейная скорость точки М.
За промежуток времени dt точка М проходит
путь dr dt.
В
то
же
время
dr Rdφ (центральный угол). Тогда,
dr Rdφ
υ
ωR
dt
dt
19.
υ ωRВ векторной форме
υ [ω, R ]
ортогонален к векторам ω
R
Вектор
и
и направлен в ту же сторону, что и векторное
произведение
[ω, R ]
20.
Период Т – промежуток времени, втечение которого тело совершает полный
оборот (т.е. поворот на угол φ 2π )
2π
Т ;
ω
Частота
ν – число оборотов тела за 1 сек.
1
ν .
Т
Угловая скорость
2π
ω
2πν;
Т
21.
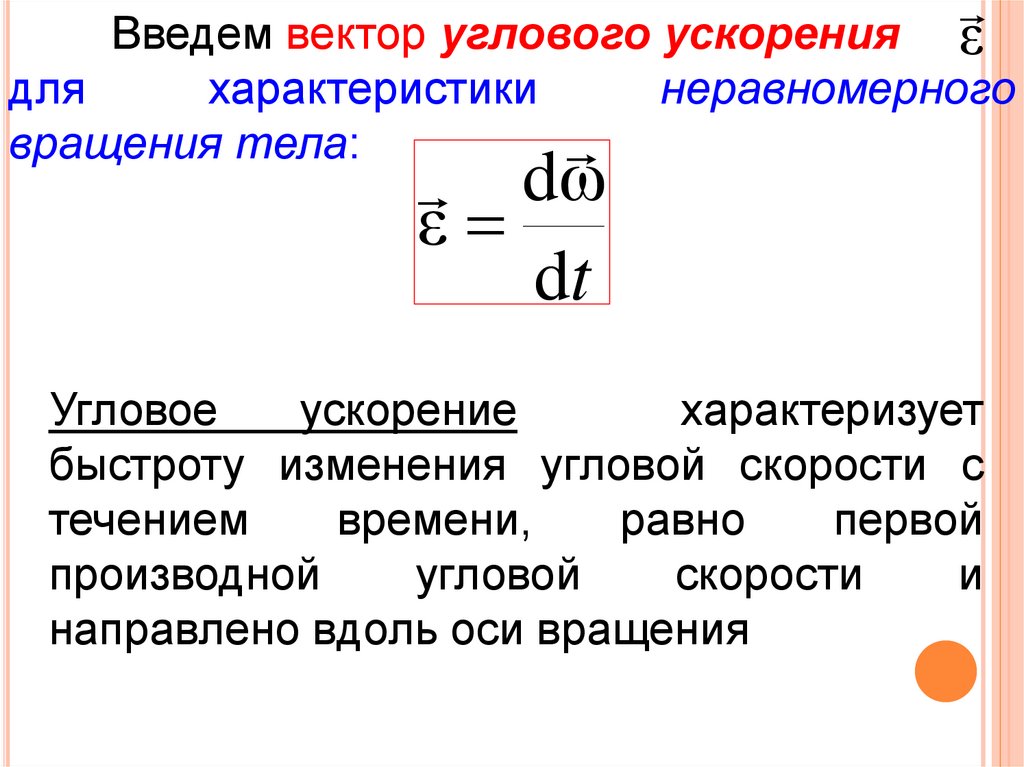
εВведем вектор углового ускорения
для
характеристики
неравномерного
вращения тела:
dω
ε
dt
Угловое
ускорение
характеризует
быстроту изменения угловой скорости с
течением
времени,
равно
первой
производной
угловой
скорости
и
направлено вдоль оси вращения
22.
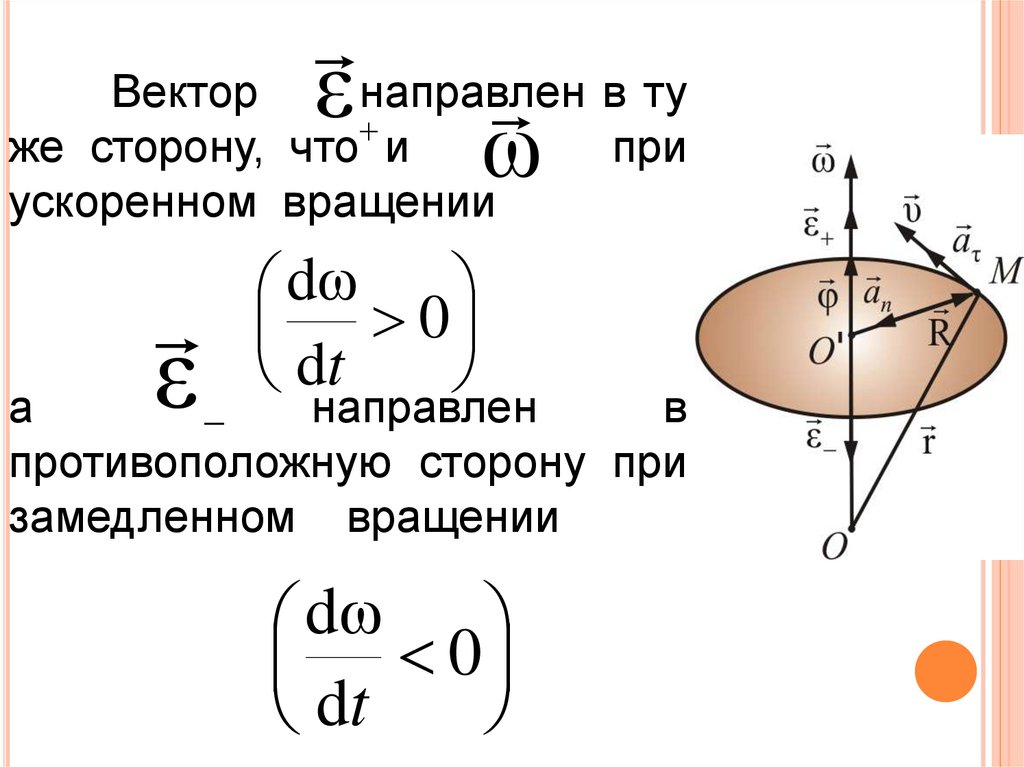
Вектор ε направленв ту
же сторону, что и
при
ω
ускоренном вращении
ε
dω 0
dt
а
направлен
в
противоположную сторону при
замедленном вращении
dω 0
dt
23.
Выразим нормальное и тангенциальноеускорения точки М через угловую скорость и
угловое ускорение:
dυ d
dω
aτ
(ωR) R
Rε;
dt dt
dt
a R ;
υ
2
an
ω R.
R
2
24.
.Ускорение
отдельной точки вращающегося тела
.
представим в виде суммы
a a an
Полное ускорение a равно:
a
2
a
2
an
2
4
R
25.
Обратите внимание.Все
кинематические
параметры,
характеризующие
вращательное
движение (угловое ускорение, угловая
скорость и угол поворота)
направлены вдоль оси
вращения.
26.
В частных случаях равномерного и равнопеременноговращения можно провести аналогию с соответствующими
случаями прямолинейного поступательного движения:
Поступательное
Вращательное
движение
движение
a 0
v const
s vt
0
const
t
a const
v v0 at
s v0t at2/2
const
0 t
0t t2/2
























 physics
physics








