Similar presentations:
Начальные геометрические сведения. Признаки равенства треугольников
1.
Начальныегеометрические
сведения
Признаки
равенства
треугольников
«Никогда
до настоящего времени мы не жили
в такой геометрический период.
…Окружающий нас мир– это мир геометрии,
чистой, истинной,
безупречной в наших глазах.
Все вокруг – геометрия»
Ле Корбюзье
Параллельные
прямые
2.
3.
ВА
4.
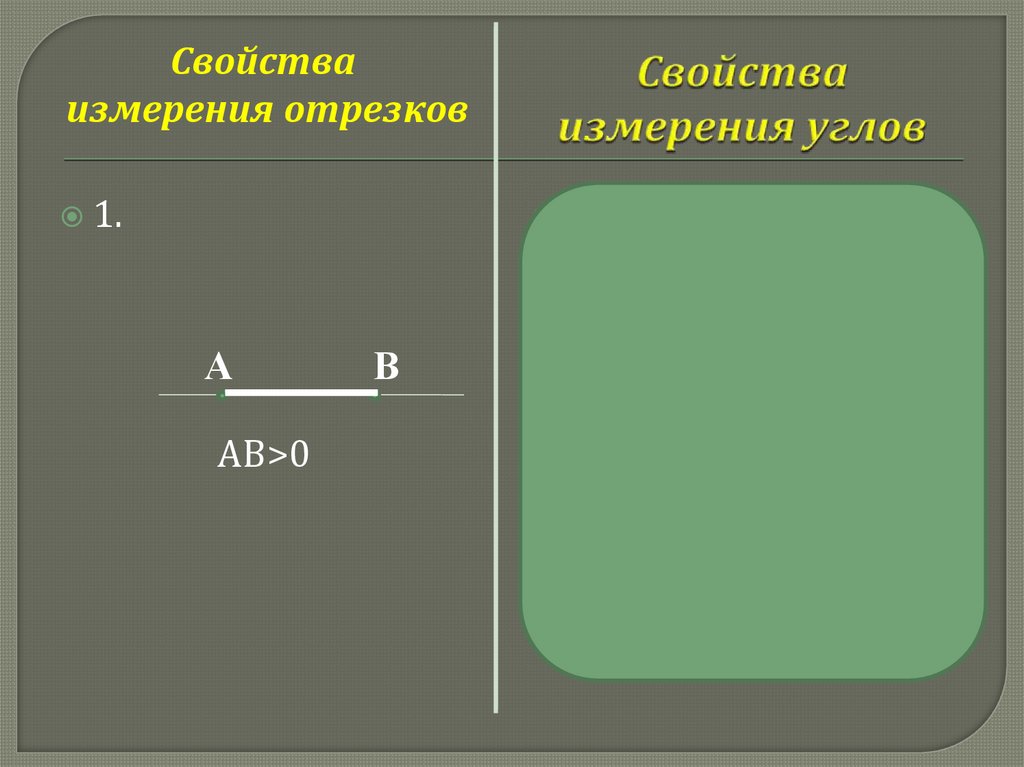
Свойстваизмерения отрезков
1.
1.
А
А
АВ>0
В
a
kº
О
B
< АОВ =kº>0
b
5.
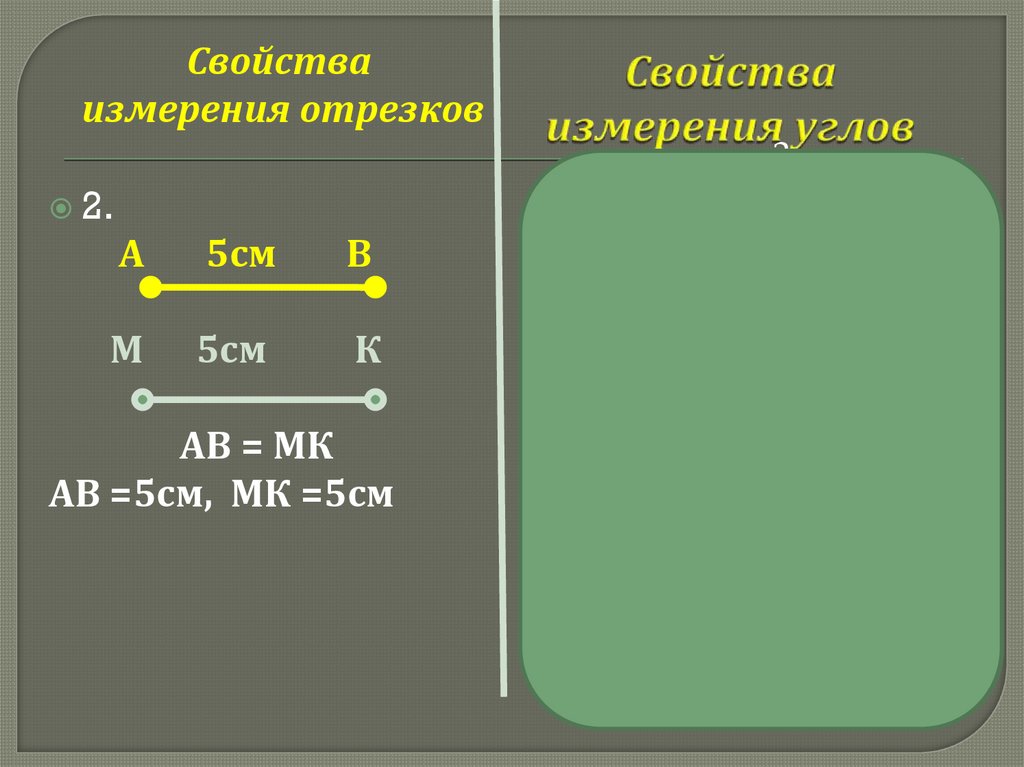
Свойстваизмерения отрезков
a
2.
А
5см
В
М
5см
К
kº
b
m
АВ = МК
АВ =5см, МК =5см
kº
n
∠ ab = ∠ mn
6.
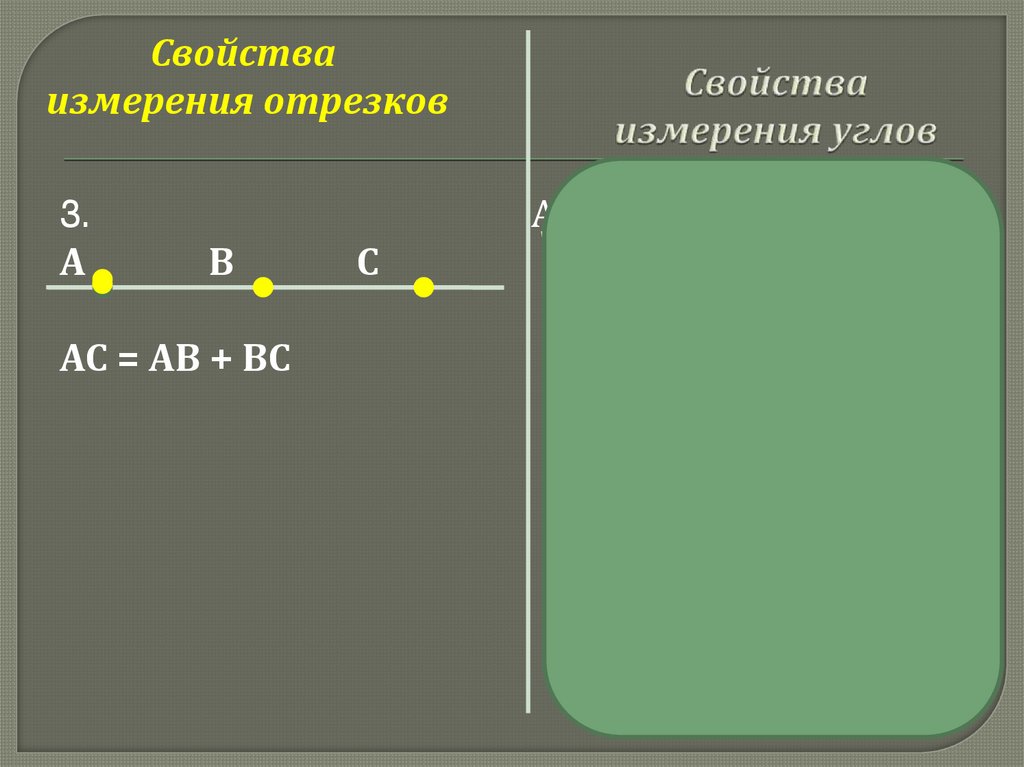
Свойстваизмерения отрезков
3.
А
А
В
С
В
АС = АВ + ВС
О
С
∠ АОС = ∠ АОВ + ∠ ВОС
7.
Дано:АВ : ВС = 4: 3,
АС = 21 см.
Найти: АВ, ВС.
А
В
С
8.
Дано:СВ на 3 см меньше АС;
АВ = 15 см.
Найти: АС, СВ.
А
С
В
9.
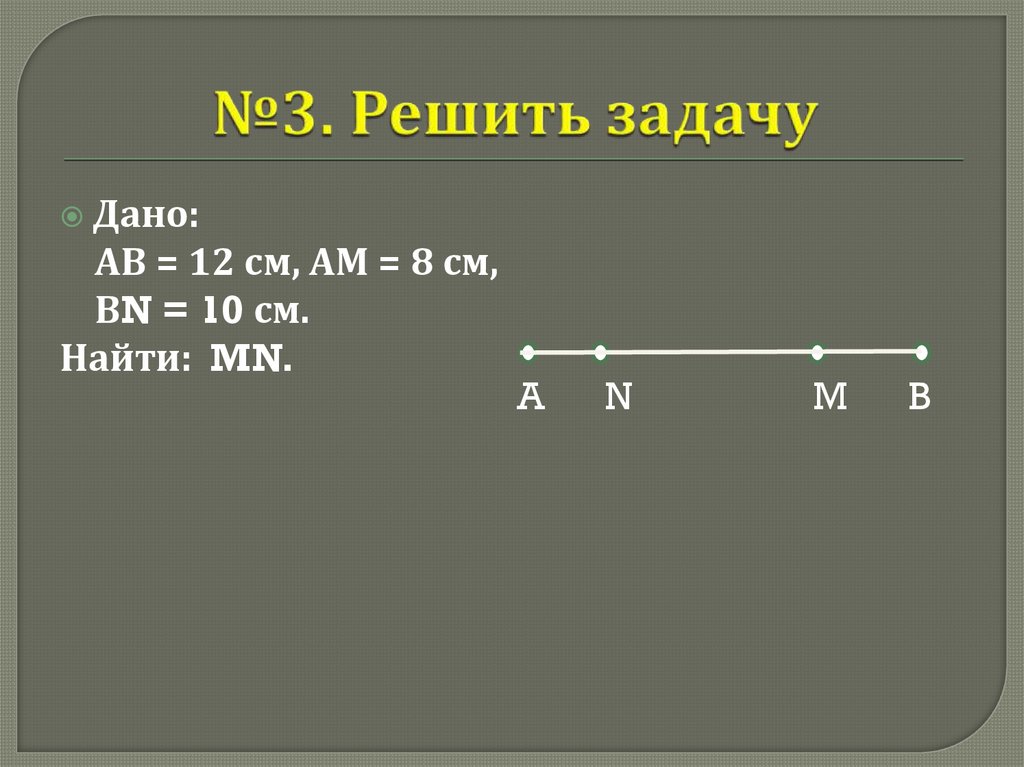
Дано:АВ = 12 см, АМ = 8 см,
ВN = 10 см.
Найти: MN.
A
N
M
B
10.
Дано:М – середина АВ,
АВ = 20 см.
Найти: АК.
А
М
К
В
11.
Дано:⅓ АК = ¼ ВК,
АВ = 14 см.
Найти: АК, ВК.
А
К
В
12.
Дано:АВ = 30 см,
АС = СД, ДЕ = ВЕ.
Найти: СЕ.
А
С
Д
Е
В
13.
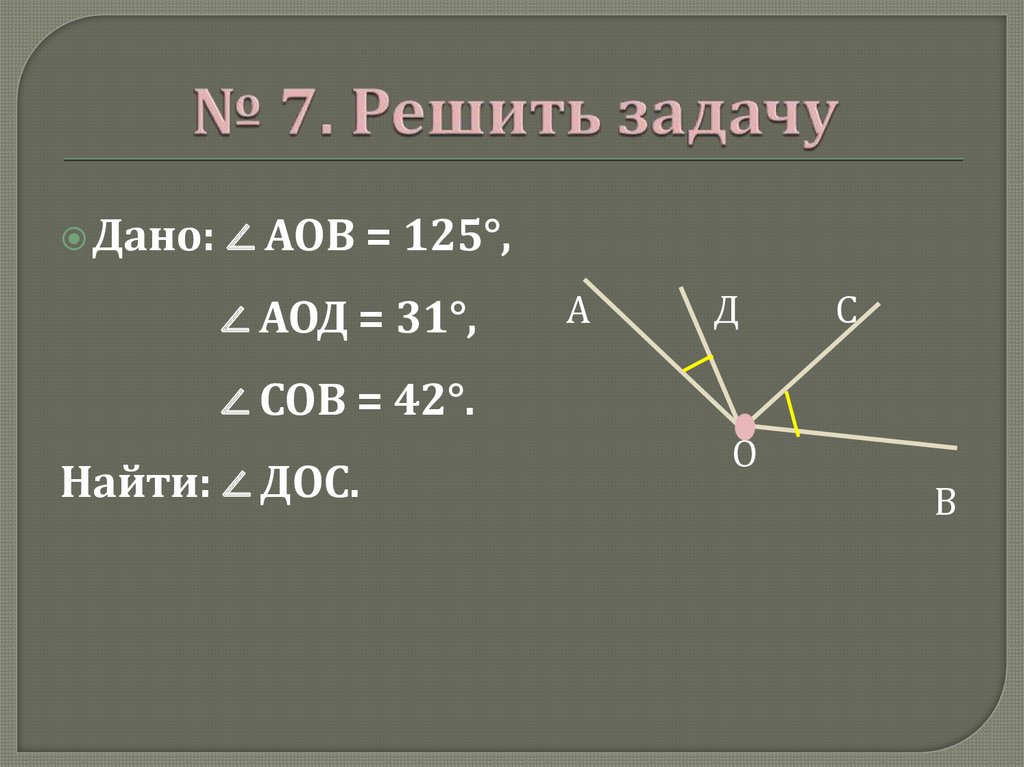
Дано:∠ АОВ = 125°,
∠ АОД = 31°,
А
Д
С
∠ СОВ = 42°.
Найти: ∠ ДОС.
О
В
14.
А) Дано: ∠ АОВ = 450680
∠ ВОС =
Найти : ∠ АОС
А
В
Б) Дано: ∠ АОВ = 450
∠ АОС = 680
Найти : ∠ ВОС
С) Дано: ∠ АОС = 450
∠ ВОС = 680
Найти : ∠ АОВ
О
С
15.
Повторение темы«Признаки равенства
треугольников.
Равнобедренный
треугольник»
16.
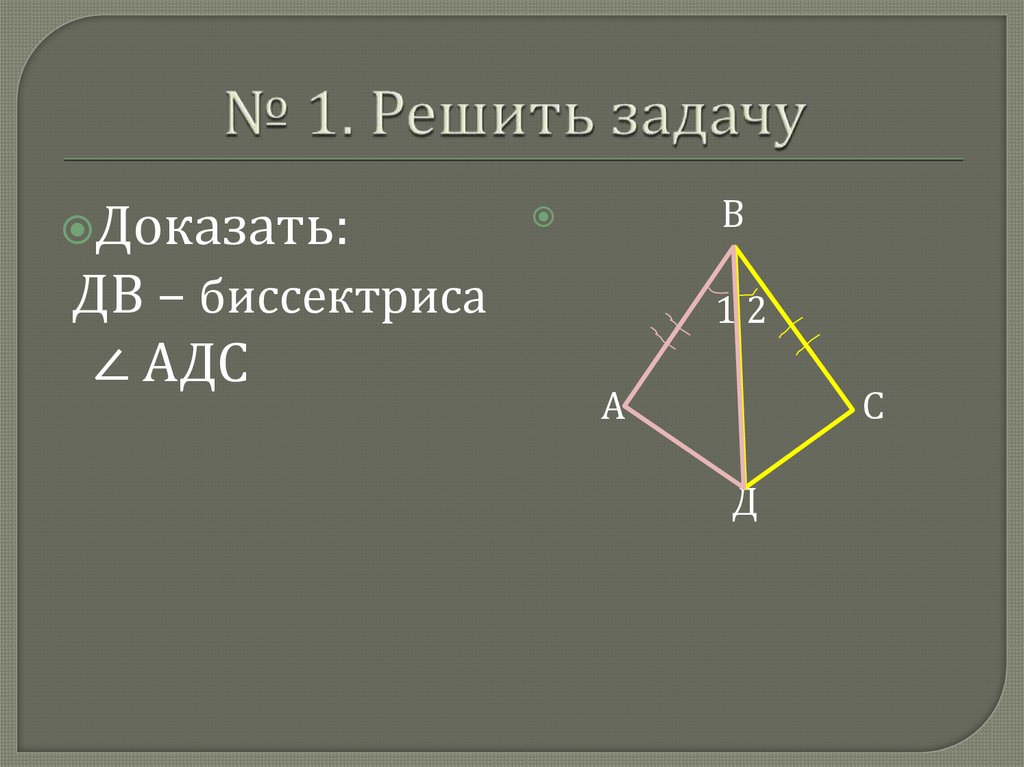
Доказать:ДВ – биссектриса
∠ АДС
В
12
А
С
Д
17.
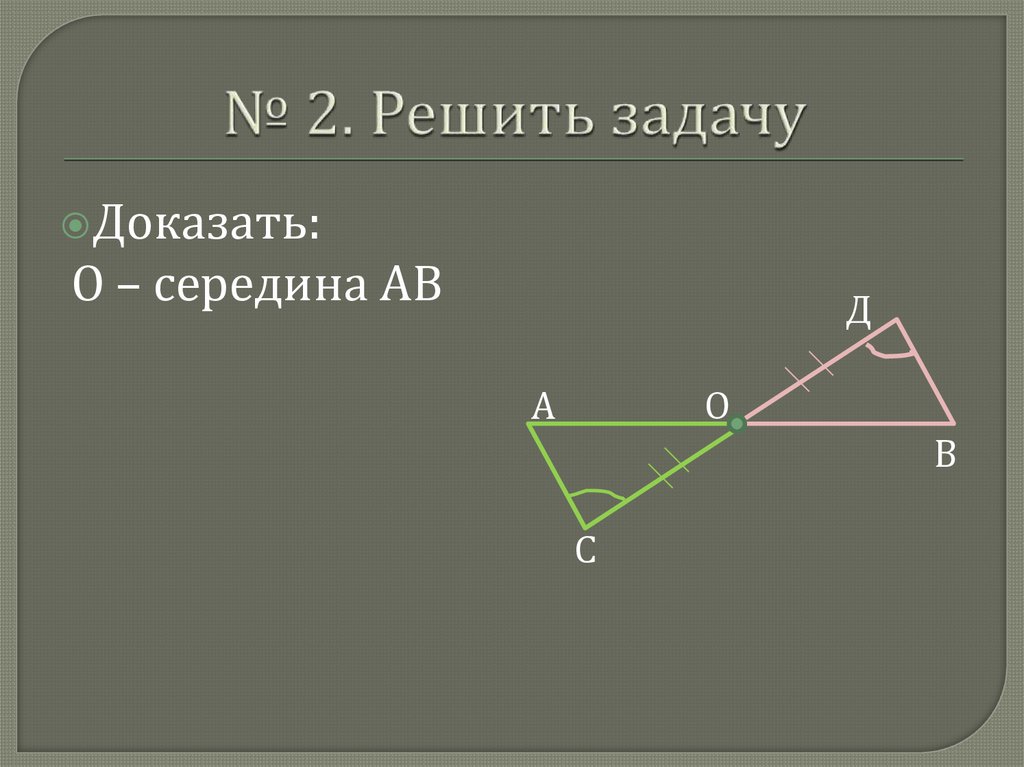
Доказать:О – середина АВ
Д
А
О
В
С
18.
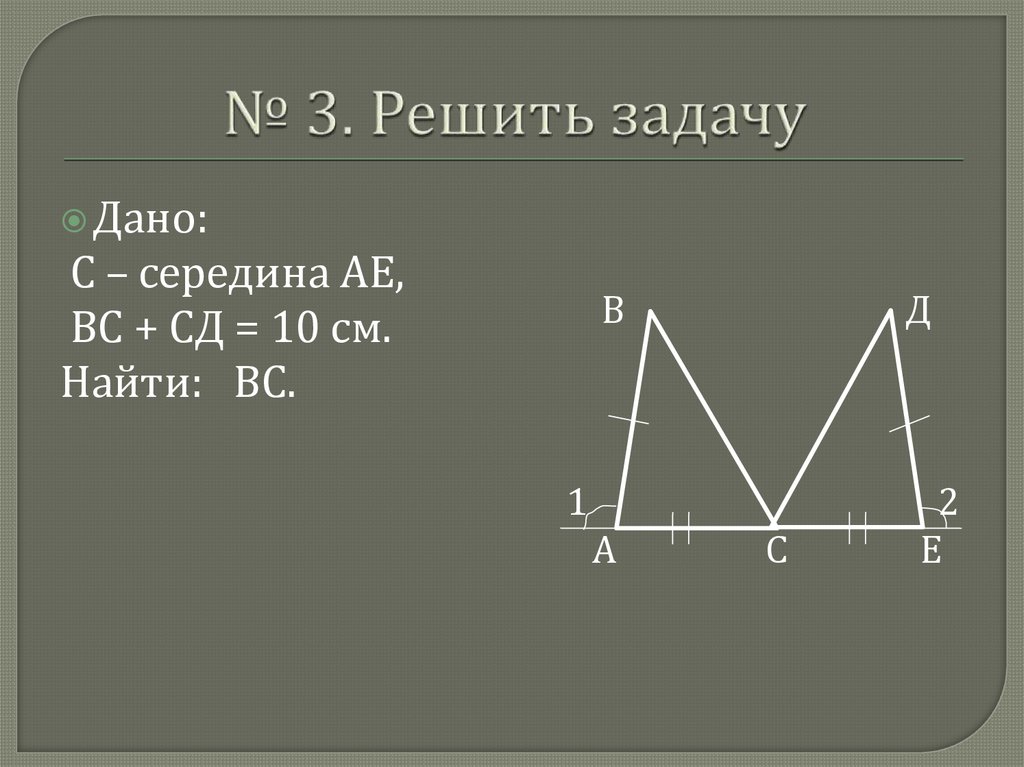
Дано:С – середина АЕ,
ВС + СД = 10 см.
Найти: ВС.
В
Д
1
А
С
2
Е
19.
Доказать:В
ВС = ДС
А
1
2
Е
3
4
Д
С
20.
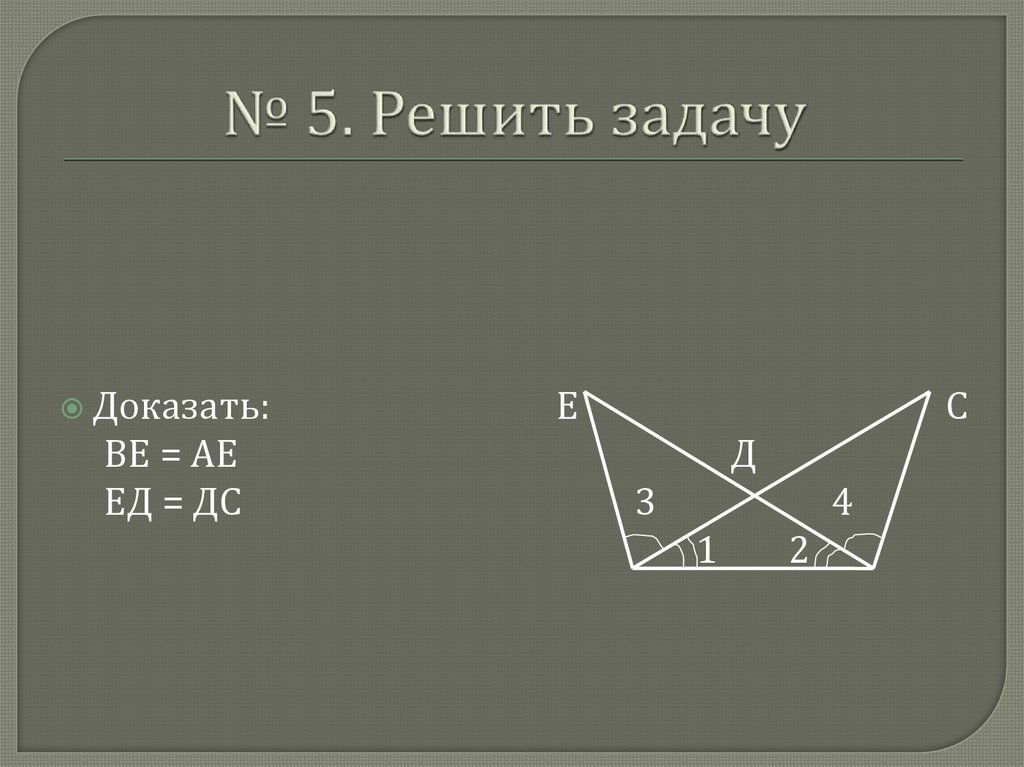
Доказать:ВЕ = АЕ
ЕД = ДС
Е
С
Д
3
4
1
2
21.
Дано:∆ АВЕ = ∆ СDF.
Доказать:
∆ ABC = ∆ CDA,
∆BEC = ∆ DFA
С
B
F
E
A
D
22.
1. рис. 5.35Найти: ∠ АВС,∠ АА1 В
2. рис. 5.36
Доказать: ∆ АВС –
равнобедренный
3. рис. 5.37.
Дано: ВС = АД
Доказать: АВ = СД.
4. рис. 5.38.
Доказать: ВД ⊥АС
23.
«Ни тридцать лет,ни тридцать столетий
не оказывают
никакого влияния на ясность
и красоту геометрических
истин»
Льюис Кэррол
Совершенствование
навыков решения
задач
Свойства
параллельных
прямых
Аксиома
параллельных
прямых
Признаки
параллельности
прямых
Урок 3
24.
1. Если а ⊥ с, b ⊥c, то:а) а||b б) a ⊥b в) ответы а) и б) неверны
2. Если а||с, b||с, то:
a)a ⊥ b б) a||b в) ответы а) и б) неверны
3. Если а ||b , с – секущая, то:
a)<2 +<3 = 180°; б) <5 = <2 в)<1+<3 =180°
а
4 2
5 3
b
1 c
25.
4.Для того, чтобы прямые а и b были
параллельными, нужно, чтобы:
а)<1+ <4 = 180°; б) <1 =<2; в) < 3 =<2
а
3 с
1
b
4
2
26.
Один из углов при пересечении двухпараллельных прямых третьей равен 52°.
Остальные углы равны:
а) 52 ° и 132 °; б) 52 ° и 128 ° в) 52°
6. Прямая МК является секущей для
прямых АВ и СД ( М ∈АВ, К ∈СД). Угол
АМК равен 78°. При каком значении угла
СКМ прямые АВ и СД могут быть
параллельны?
а)102 ° б) 12 ° в) 78 ° г) 78 ° и 102 °
5.
27.
1 – а)2 – б)
3 – в)
4 – в)
5 – б)
6 – г)
28.
Задача№1.
Найти:
параллельные прямые
а
47° m
123°
b
c
133°
29.
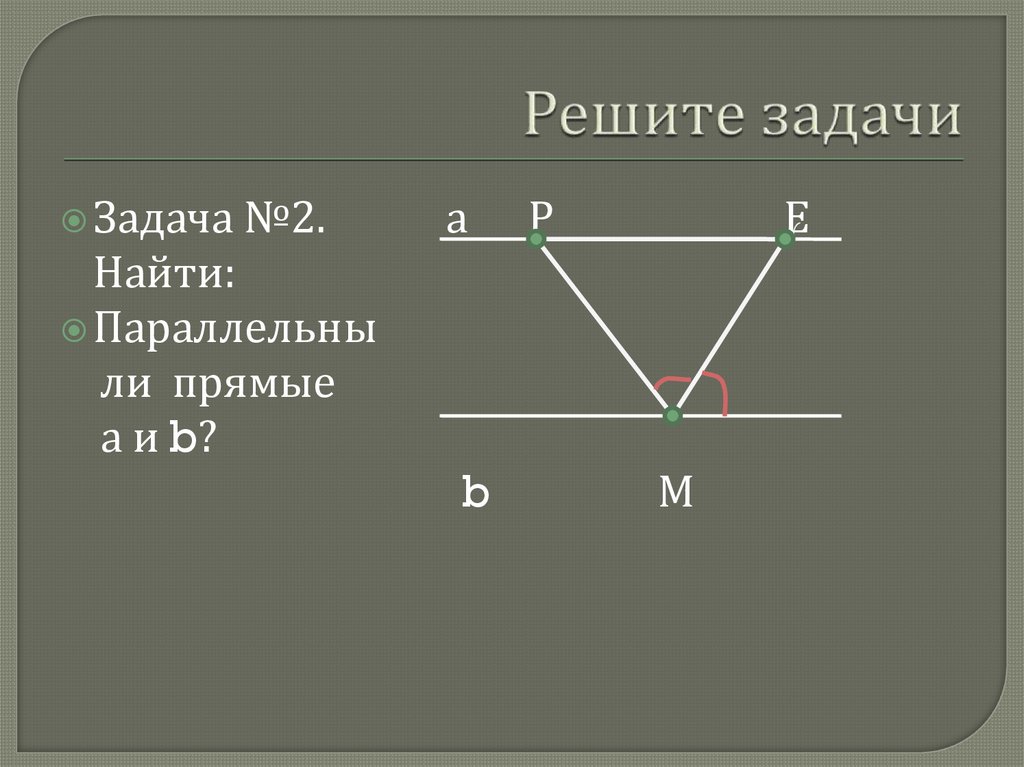
Задача№2.
а
Р
Е
Найти:
Параллельны
ли прямые
а и b?
b
М
30.
NЗадача №3. Найти:
параллельны ли
прямые a и b?
60°
110°
M
K
с
Задача № 4.
Найти: угол 1, угол 2
a
b
b
d
80° 2 1
80°
130°
31.
са
Задача 4. Дано: а ∥ b
Найти :∠ 1, ∠ 2.
1
b
2
800
с
Задача 5.
Дано: а || b
Найти: ∠ 1, ∠ 2.
а
1
2
b
500
32.
Задача №7Найти: ∠ 1, ∠ 2.
33.
Задача № 8Найти: ∠ 1
34.
Задача № 9Найти: ∠ 1
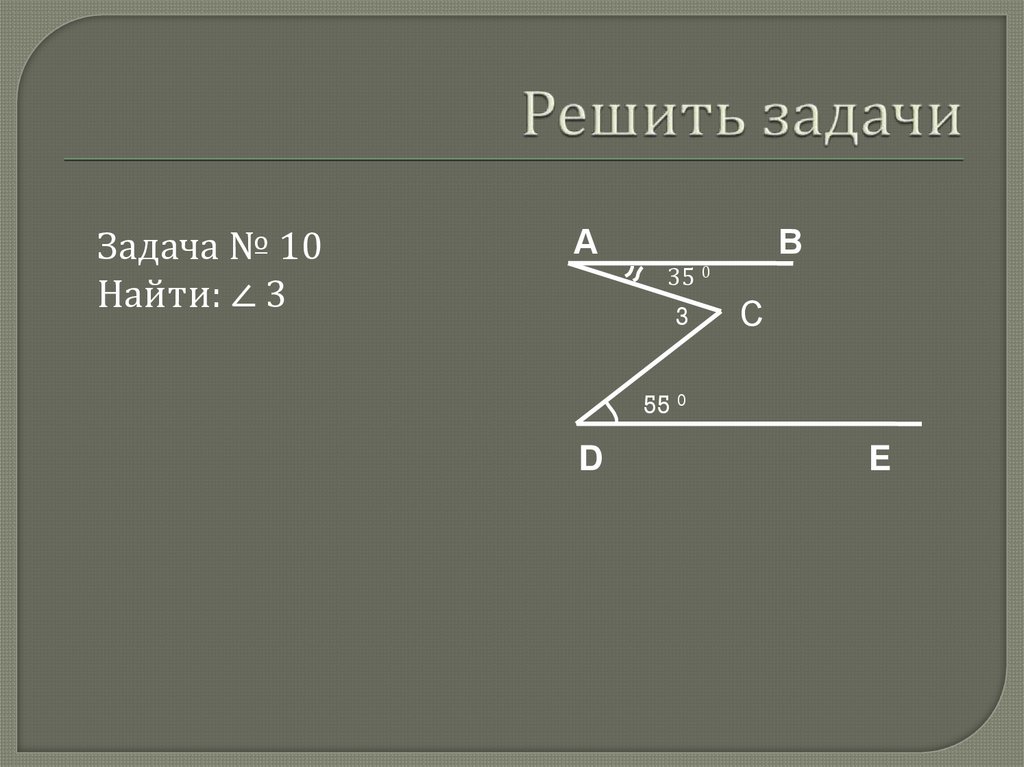
35.
Задача № 10Найти: ∠ 3
А
В
35 0
3
С
55 0
D
E
36.
«Никогдадо настоящего времени мы не жили
в такой геометрический период.
…Окружающий нас мир
– это мир геометрии, чистой, истинной,
безупречной в наших глазах.
Все вокруг – геометрия»
Ле Корбюзье
























 mathematics
mathematics








