Решение задач на вычисление площадей фигур

1.

Тема урока: Решение задач на
вычисление площадей фигур.
ЦЕЛЬ УРОКА:
НАУЧИТЬСЯ ПРИМЕНЯТЬ ИЗВЕСТНЫЕ
ФОРМУЛЫ ДЛЯ НАХОЖДЕНИЯ ПЛОЩАДЕЙ
ФИГУР.

2.

Проверка домашнего задания:

3.

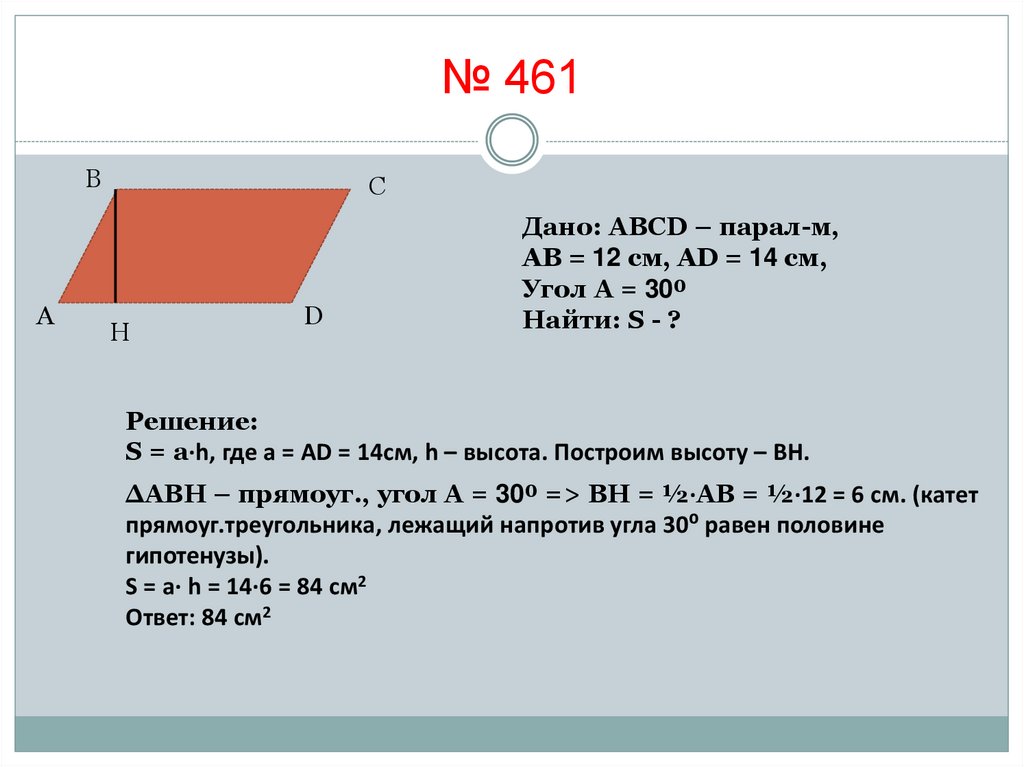
№ 461
В
А
С
H
D
Дано: АВСD – парал-м,
АВ = 12 см, АD = 14 см,
Угол А = 30⁰
Найти: S - ?
Решение:
S = a·h, где а = AD = 14см, h – высота. Построим высоту – ВH.
ΔABH – прямоуг., угол А = 30⁰ => BH = ½·AB = ½·12 = 6 см. (катет
прямоуг.треугольника, лежащий напротив угла 30⁰ равен половине
гипотенузы).
S = a· h = 14·6 = 84 см2
Ответ: 84 см2

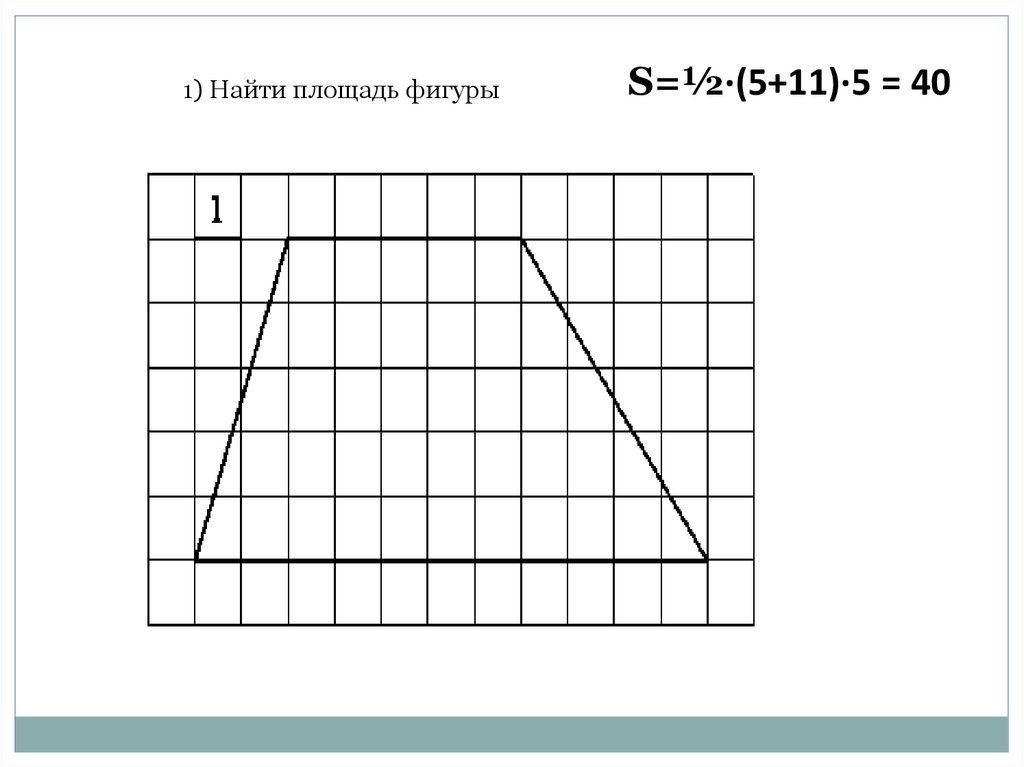
4.

1) Найти площадь фигуры
S=½·(5+11)·5 = 40

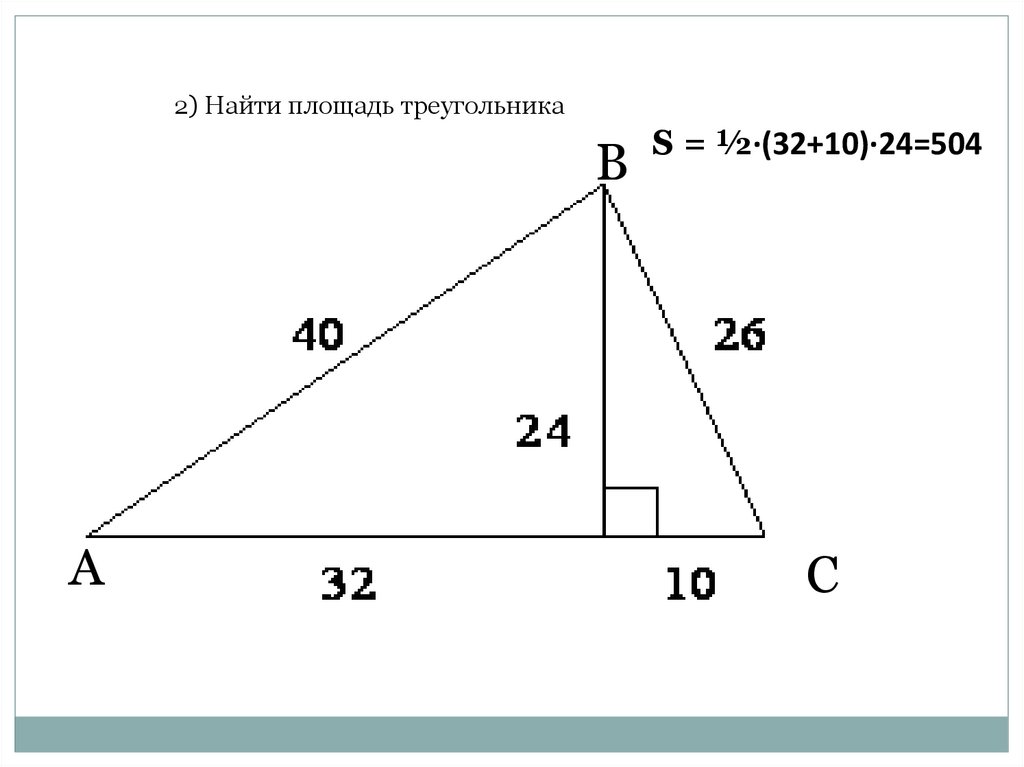
5.

2) Найти площадь треугольника
В
А
S = ½·(32+10)·24=504
С

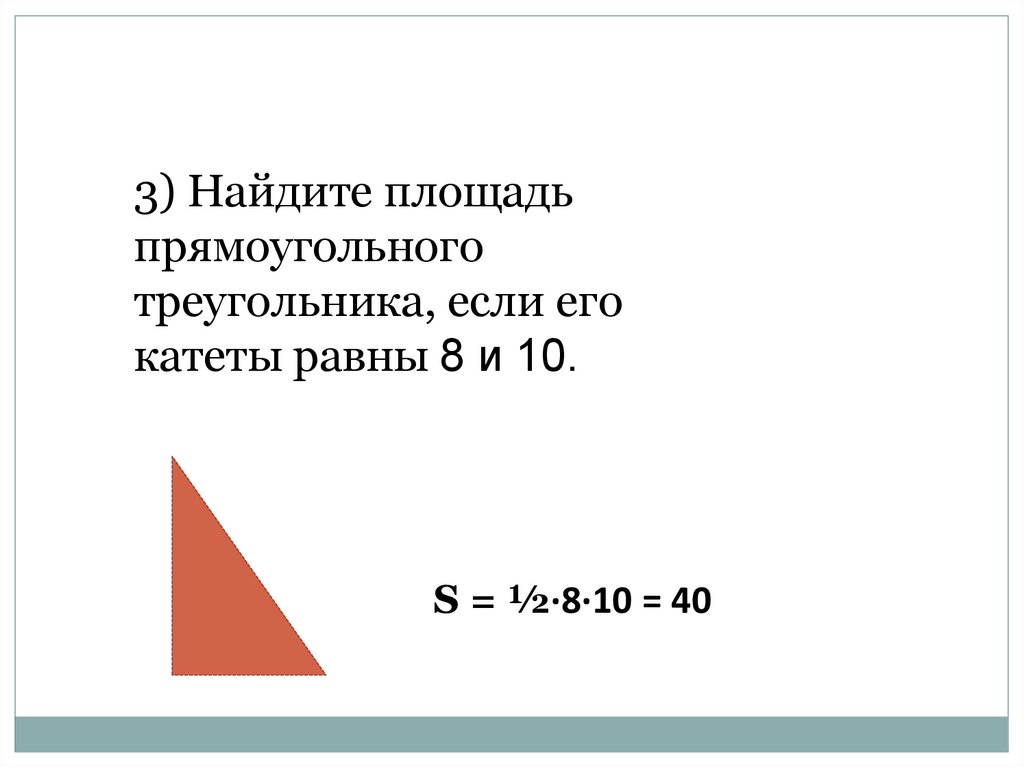
6.

3) Найдите площадь
прямоугольного
треугольника, если его
катеты равны 8 и 10.
S = ½·8·10 = 40

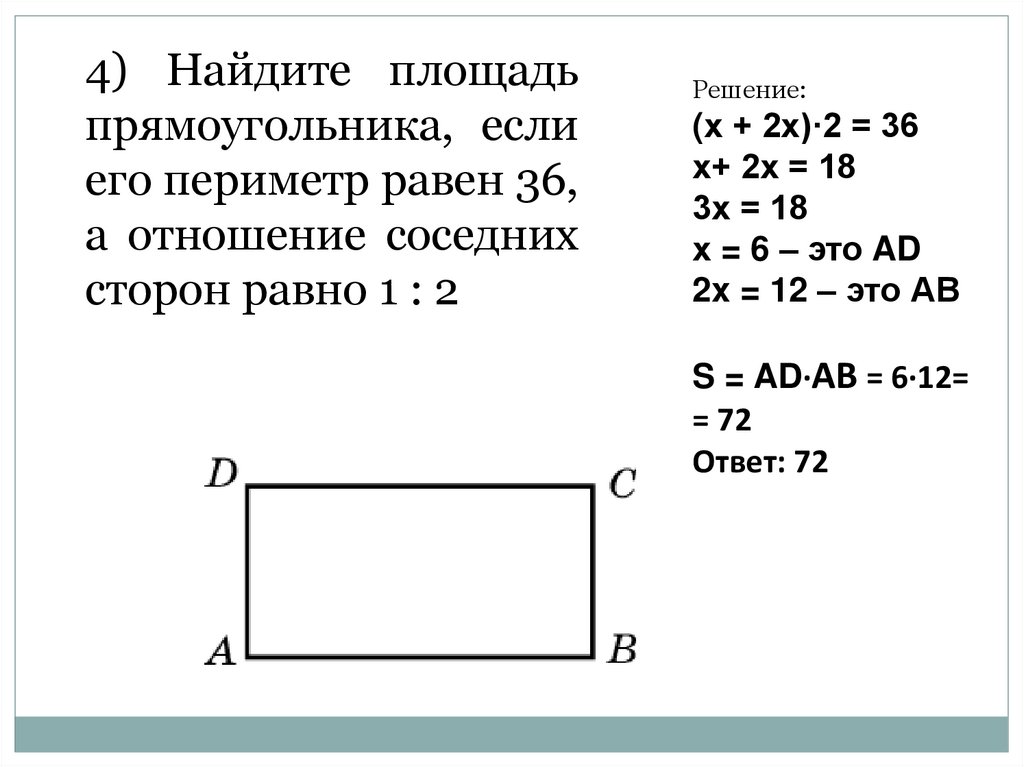
7.

4) Найдите площадь
прямоугольника, если
его периметр равен 36,
а отношение соседних
сторон равно 1 : 2
Решение:
(х + 2х)·2 = 36
х+ 2х = 18
3х = 18
х = 6 – это AD
2x = 12 – это АВ
S = AD·AB = 6·12=
= 72
Ответ: 72

8.

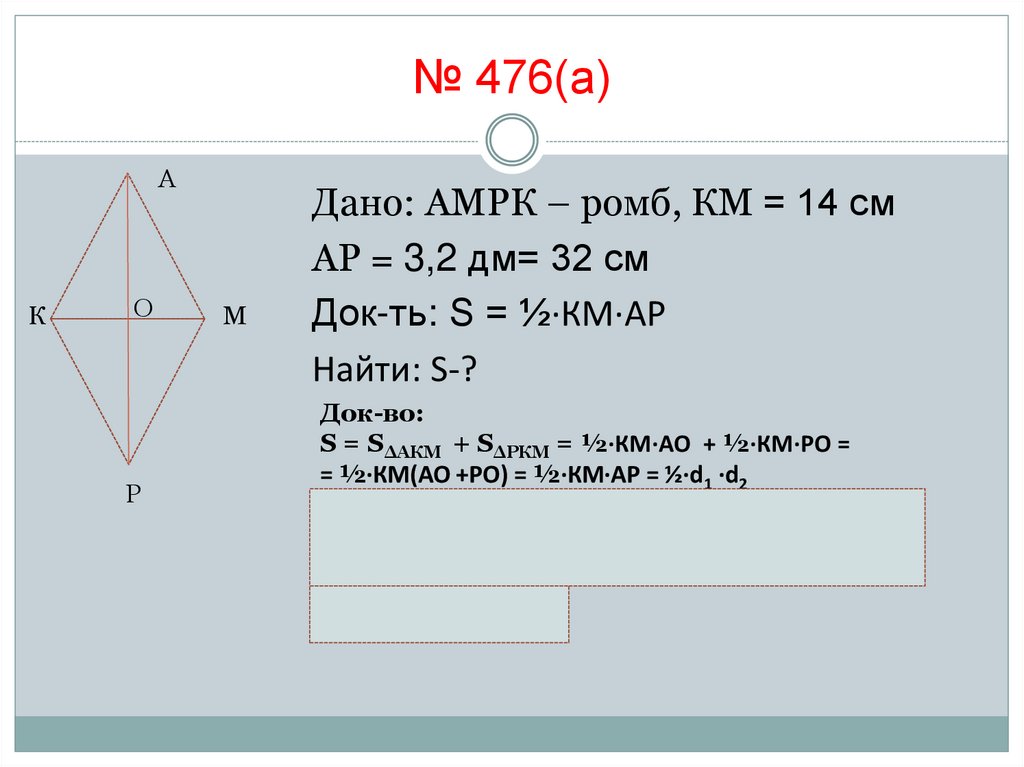
№ 476(а)
А
К
О
Р
М
Дано: АМРК – ромб, КМ = 14 см
АР = 3,2 дм= 32 см
Док-ть: S = ½·КМ·АР
Найти: S-?
Док-во:
S = SΔАКМ + SΔРКМ = ½·КМ·АО + ½·КМ·РО =
= ½·КМ(АО +РО) = ½·КМ·АР = ½·d1 ·d2
S = ½·d1 ·d2
Площадь ромба равна половине произведения его
диагоналей.
S = ½·32·14 = 224 см2
Ответ: 224 см2

9.

Домашнее задание:
№ 476(б), № 480(б)

10.

Дополнительно:

11.

Спасибо за урок!!!!!!!

12.

С
е
г
о
д
н
я