2.01M

Category: $mathematics$ mathematics

Математика ЕГЭ. Вероятность, часть II

2.

Введение
Тема
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

Теория
Вероятность
Вероятность = Кол-во подходящих событий
Кол-во возможных событий
Вероятность изменяется от 0 до 1
Вероятность
Вероятность подходящих событий +
Вероятность неподходящих событий = 1
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

4.

Теория
Вероятность нескольких событий
1
Подсчитываем вероятность каждого события в отдельности
2
Между дробями ставим знаки:
Умножить, если нужно первое И второе событие.
Сложить, если нужно первое ИЛИ второе событие.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

5.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
1. Наступит исход ООР (в первый и второй разы выпадет орёл, в третий – решка).
Решение:
ОРЁЛ
1
2
1
РЕШКА
2
1 1 1 1
· · = = 0,125
2 2 2 8
Ответ:
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
0,125

6.

7.

8.

9.

10.

11.

12.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
2. Орёл выпадет три раза.
Решение:
ОРЁЛ
1
2
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

13.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
2. Орёл выпадет три раза.
Решение:
ОРЁЛ
1
2
1
РЕШКА
2
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

14.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
2. Орёл выпадет три раза.
Решение:
ОРЁЛ
1
2
1
РЕШКА
2
1 1 1 1
· · = = 0,125
2 2 2 8
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

15.

16.

17.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
2. Орёл выпадет три раза.
Решение:
ОРЁЛ
1
2
1
РЕШКА
2
1 1 1 1
· · = = 0,125
2 2 2 8
Ответ:
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
0,125

18.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
3. Орёл выпадет два раза.
Решение:
ОРЁЛ
ОРЁЛ
РЕШКА
ОРЁЛ
РЕШКА
ОРЁЛ
РЕШКА
ОРЁЛ
ОРЁЛ
1
8
1
8
1
8
+
=
+
3
8
=
0,375
Ответ:
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
0,375

19.

20.

21.

22.

23.

24.

25.

26.

Задание №
1
В случайном эксперименте симметричную монету
бросают трижды. Найдите вероятность того, что:
4. Орёл выпадет не более одного раза.
Решение:
РЕШКА
РЕШКА РЕШКА
ОРЕЛ
РЕШКА РЕШКА
РЕШКА
ОРЕЛ
РЕШКА
РЕШКА ОРЕЛ
РЕШКА
1
8
1
8
1
8
1
8
+
+
=
0,5
1 − 0,5 = 0,5
+
Ответ:
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании
0,5

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

Задание №
1
2
2
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих
матчах команда «Биолог» начнёт игру с мячом ровно один раз.
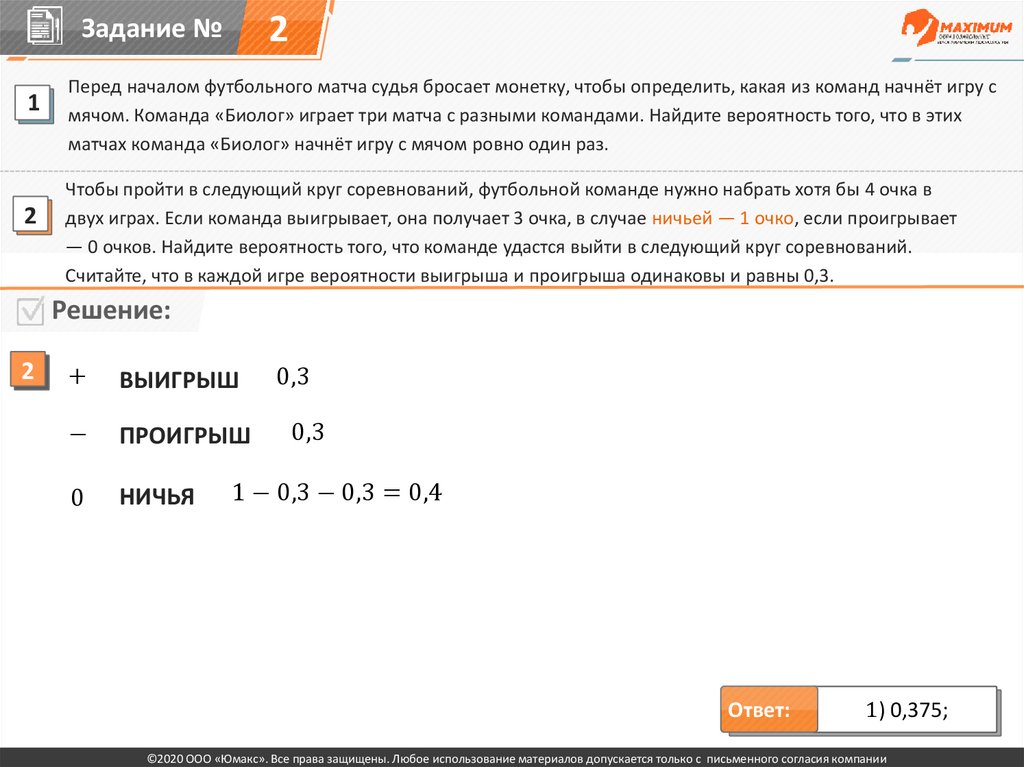
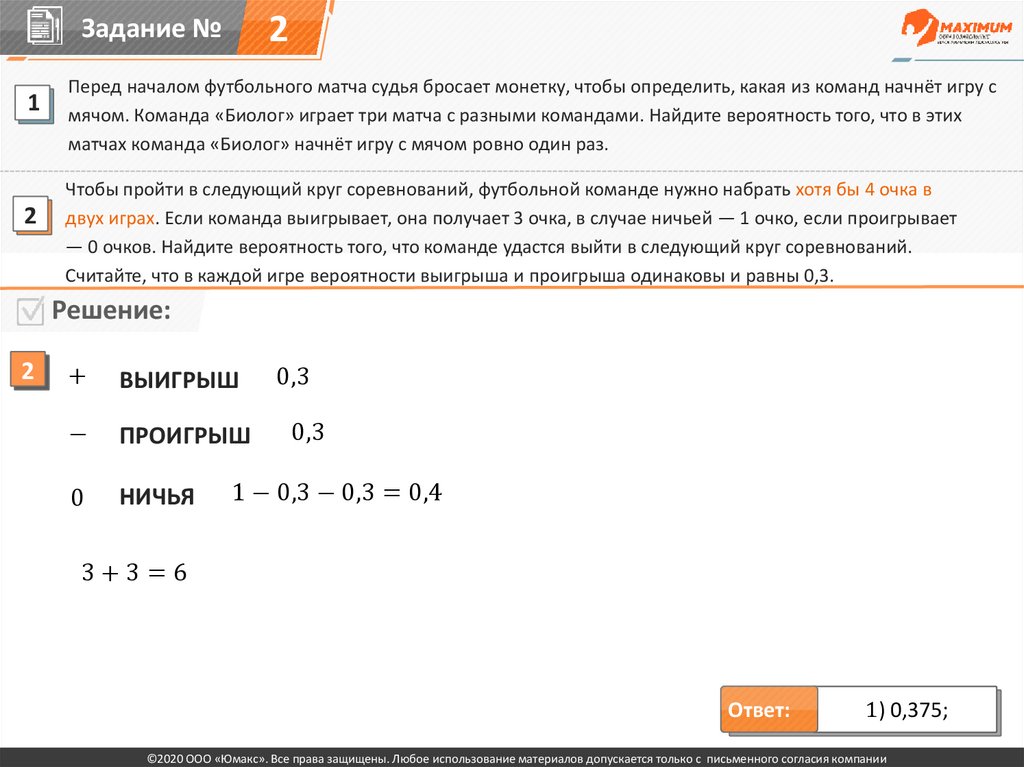
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в
двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает
— 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований.
Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение:
1
+
−
−
−
+
−
−
−
+
1
8
+
1
8
1
8
=
+
3
8
=
0,375
Ответ:
1) 0,375;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

38.

39.

40.

41.

42.

43.

44.

45.

2
Задание №
1
2
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих
матчах команда «Биолог» начнёт игру с мячом ровно один раз.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в
двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает
— 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований.
Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение:
2
+
ВЫИГРЫШ
−
ПРОИГРЫШ
0
НИЧЬЯ
3+3=6
3+1=4
1+3=4
0,3
0,3
1 − 0,3 − 0,3 = 0,4
+
+
0,3·0,3 = 0,09
+
0
0
0,3·0,4 = 0,12
+
0,4·0,3 = 0,12
+
=
0,33
+
Ответ:
1) 0,375;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

2
Задание №
1
2
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с
мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих
матчах команда «Биолог» начнёт игру с мячом ровно один раз.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в
двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает
— 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований.
Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение:
2
+
ВЫИГРЫШ
−
ПРОИГРЫШ
0
НИЧЬЯ
3+3=6
3+1=4
1+3=4
0,3
0,3
1 − 0,3 − 0,3 = 0,4
+
+
0,3·0,3 = 0,09
+
0
0
0,3·0,4 = 0,12
+
0,4·0,3 = 0,12
+
=
0,33
+
Ответ:
1) 0,375; 2) 0,33.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

59.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
1
Вероятность = Вероятность + Вероятность
(больше года)
(больше двух лет)
(от 1 до 2 лет)
Тогда: Вероятность = Вероятность - Вероятность = 0,98 − 0,84 = 0,14.
(от 1 до 2 лет)
(больше года)
(больше двух лет)
Ответ:
1) 0,14;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

60.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
1
Вероятность = Вероятность + Вероятность
(больше года)
(больше двух лет)
(от 1 до 2 лет)
Тогда: Вероятность = Вероятность - Вероятность = 0,98 − 0,84 = 0,14.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

61.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
1
Вероятность = Вероятность + Вероятность
(больше года)
(больше двух лет)
(от 1 до 2 лет)
Тогда: Вероятность = Вероятность - Вероятность = 0,98 − 0,84 = 0,14.
(от 1 до 2 лет)
(больше года)
(больше двух лет)
0,93
0,82
Ответ:
1) 0,14;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

62.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
1
Вероятность = Вероятность + Вероятность
(больше года)
(больше двух лет)
(от 1 до 2 лет)
Тогда: Вероятность = Вероятность - Вероятность = 0,93 − 0,82 = 0,11.
(от 1 до 2 лет)
(больше года)
(больше двух лет)
0,93
0,82
Ответ:
1) 0,14;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

63.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
1
Вероятность = Вероятность + Вероятность
(больше года)
(больше двух лет)
(от 1 до 2 лет)
Тогда: Вероятность = Вероятность - Вероятность = 0,93 − 0,82 = 0,11.
(от 1 до 2 лет)
(больше года)
(больше двух лет)
0,93
0,82
Ответ:
1) 0,11;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

64.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
Вероятность = Вероятность + Вероятность
2
(больше 5 задач) (больше 6 задач)
(6 задач)
Ответ:
1) 0,11;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

65.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
Вероятность = Вероятность + Вероятность
2
(больше 5 задач) (больше 6 задач)
(6 задач)
0,83 = 0,77+ Вероятность
(6 задач)
Ответ:
1) 0,11; 0,06.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

66.

Задание №
3
1
Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он
прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух
лет, но больше года.
2
Вероятность того, что на тестировании по физике учащийся А. верно решит больше 6 задач, равна
0,77. Вероятность того, что А. верно решит больше 5 задач, равна 0,83. Найдите вероятность того,
что А. верно решит ровно 6 задач.
Решение:
Вероятность = Вероятность + Вероятность
2
(больше 5 задач) (больше 6 задач)
(6 задач)
0,83 = 0,77+ Вероятность
(6 задач)
0,83 - 0,77 = 0,06
Ответ:
1) 0,11; 0,06.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

67.

Задание №
1
2
3
4
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
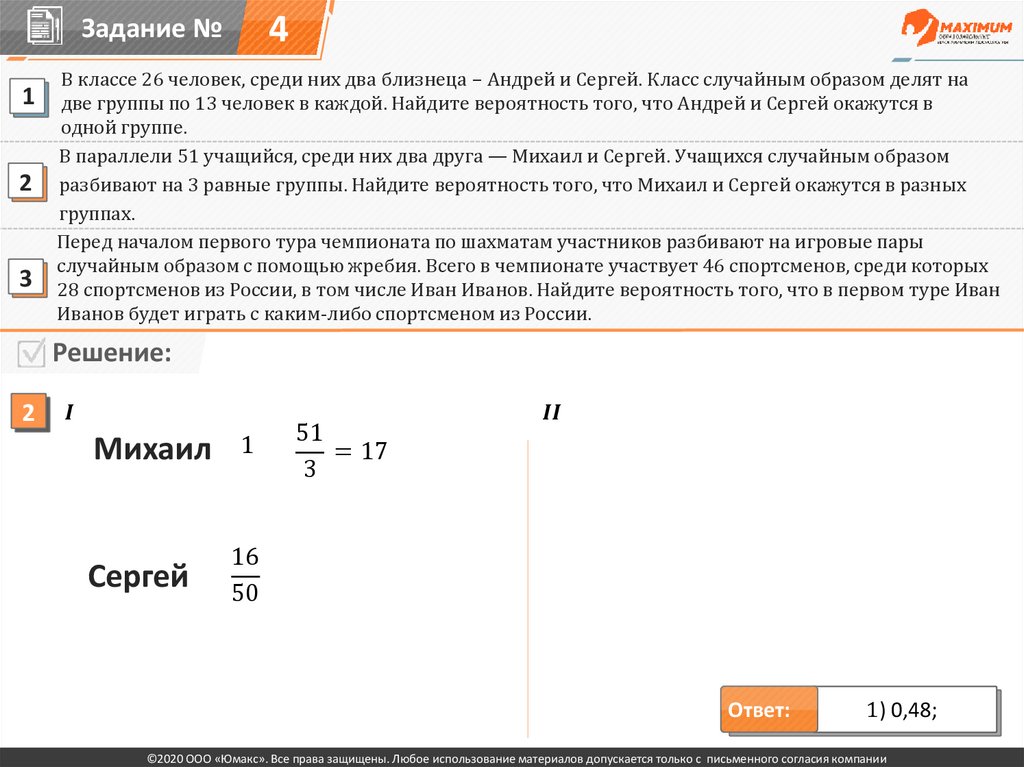
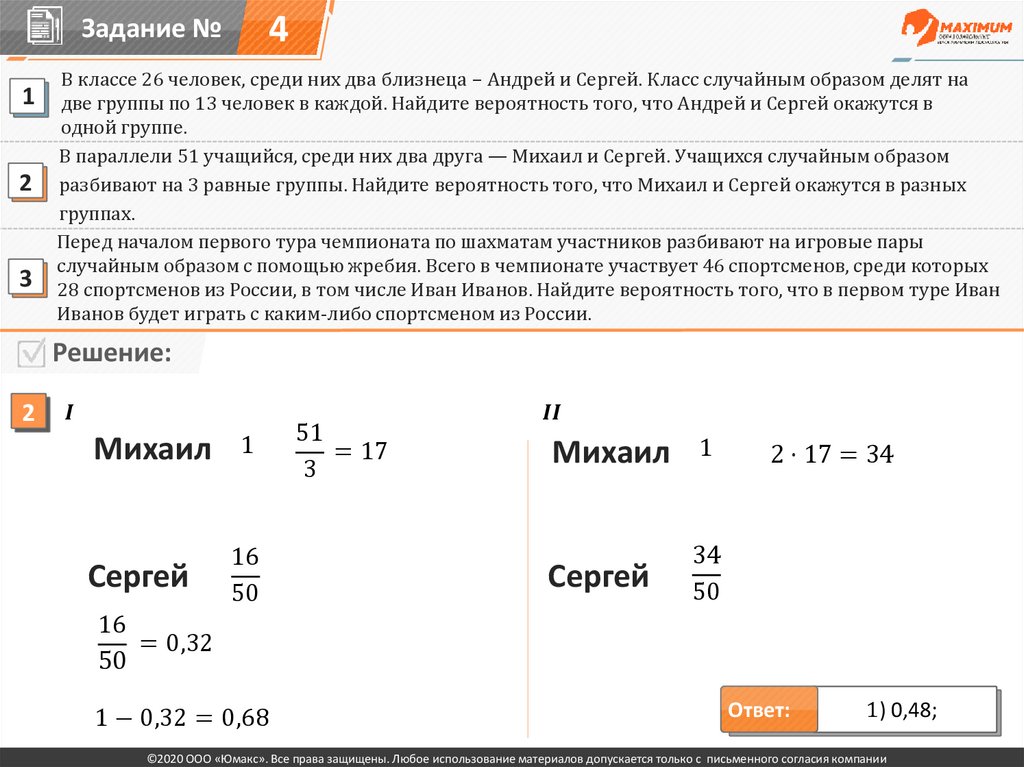
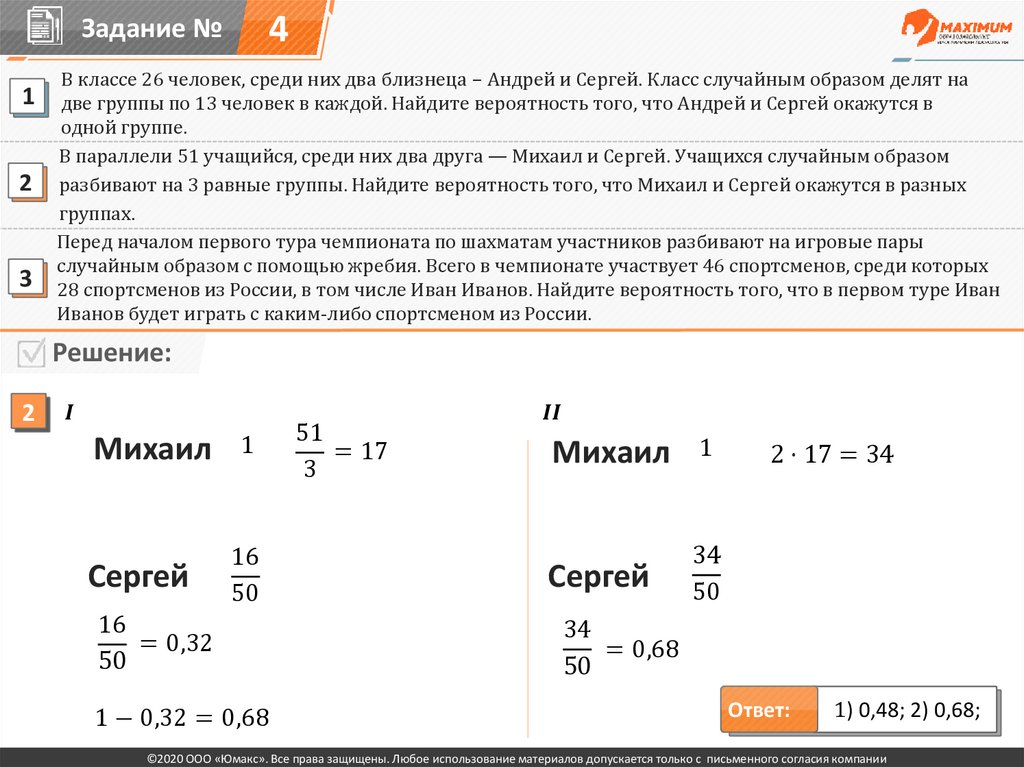
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
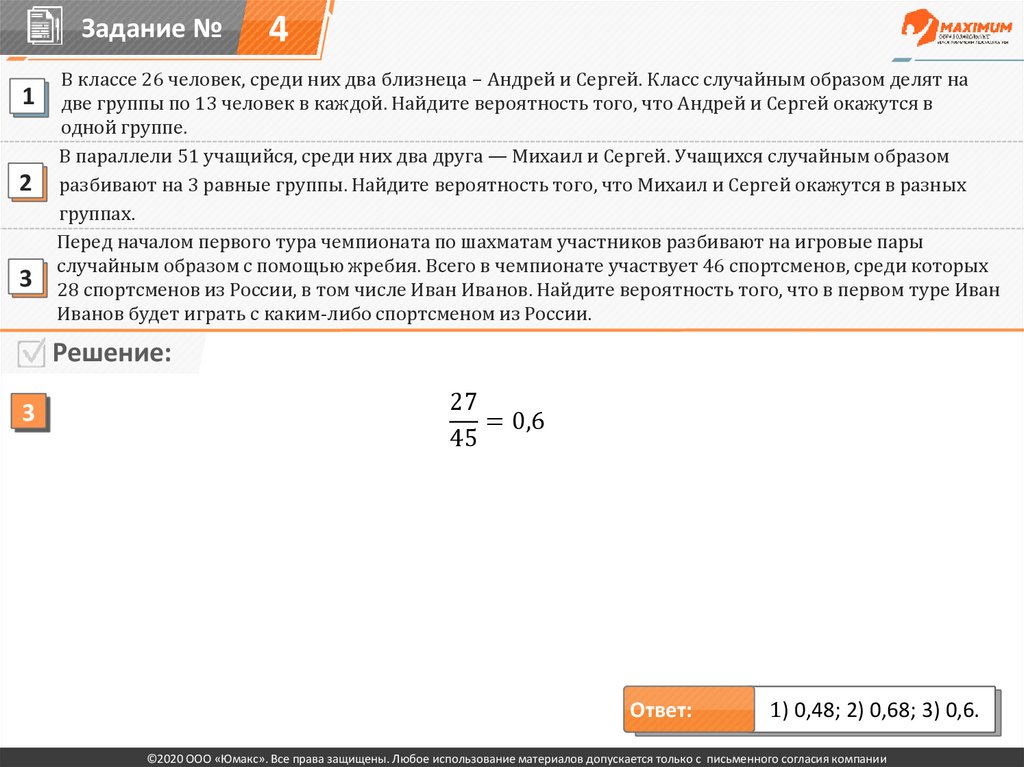
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

68.

4
Задание №
1
2
3
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
Андрей
1
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

69.

4
Задание №
1
2
3
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
Андрей
1
Сергей
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

70.

4
Задание №
1
2
3
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
Андрей
1
Сергей
12
25
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

71.

4
Задание №
1
2
3
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
Андрей
1
Сергей
12
25
12
= 0,48
25
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

72.

4
Задание №
1
2
3
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
1
Андрей
1
Сергей
12
25
12
= 0,48
25
Ответ:
1) 0,48;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

73.

Теория
В случаях, когда выбранный предмет/человек не
участвует в повторном выборе, после каждого выбора
количество
подходящих
и
возможных
вариантов
уменьшается на единицу.
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

74.

Задание №
1
2
3
4
В классе 26 человек, среди них два близнеца − Андрей и Сергей. Класс случайным образом делят на
две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в
одной группе.
В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом
разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в разных
группах.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары
случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых
28 спортсменов из России, в том числе Иван Иванов. Найдите вероятность того, что в первом туре Иван
Иванов будет играть с каким-либо спортсменом из России.
Решение:
2
Ответ:
1) 0,48;
©2020 ООО «Юмакс». Все права защищены. Любое использование материалов допускается только с письменного согласия компании

75.

English Русский Rules