Similar presentations:
Решение задач повышенной сложности. (Часть 2)
1.
РЕШЕНИЕ ЗАДАЧПОВЫШЕННОЙ СЛОЖНОСТИ
Часть 2
Рабчук Людмила Васильевна
доцент кафедры физики УГАТУ
доцент кафедры физики, математики и информатики ИРО РБ
2. Задача 1
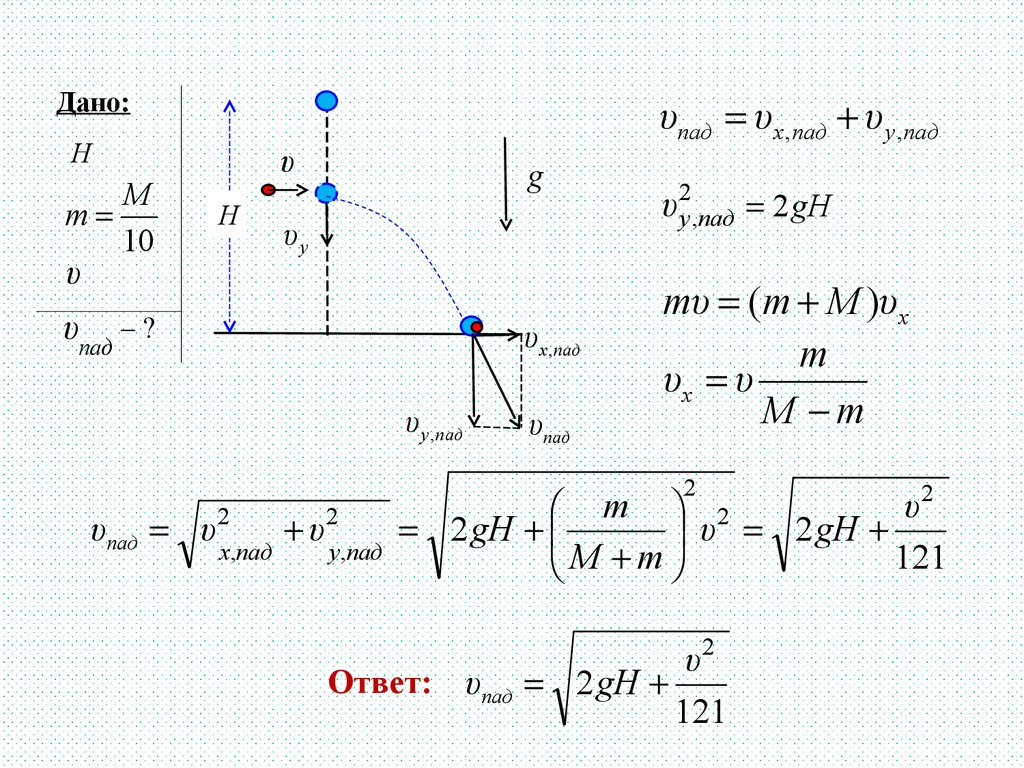
С высоты Н падает шар. Когда он пролетал мимоокна, в него в горизонтальном направлении
выстрелили из ружья. Пуля застряла в центре шара.
С какой скоростью шар упадет на землю? Пуля легче
шара в 10 раз, ее скорость равна υ .
(Всероссийская аэрокосмическая
олимпиада)
3.
Дано:υ
Н
M
m
10
Н
υ
g
υу
υх ,пад
υпад – ?
υ у ,пад
υпад
υпад υх ,пад υ у ,пад
υ 2у ,пад 2 gH
mυ (m M )υx
m
υx υ
M m
2
υпад υ 2
х ,пад
υ2
у ,пад
υ2
m 2
2 gH
υ 2 gH
121
M m
Ответ: υпад
υ2
2 gH
121
4. Задача 2
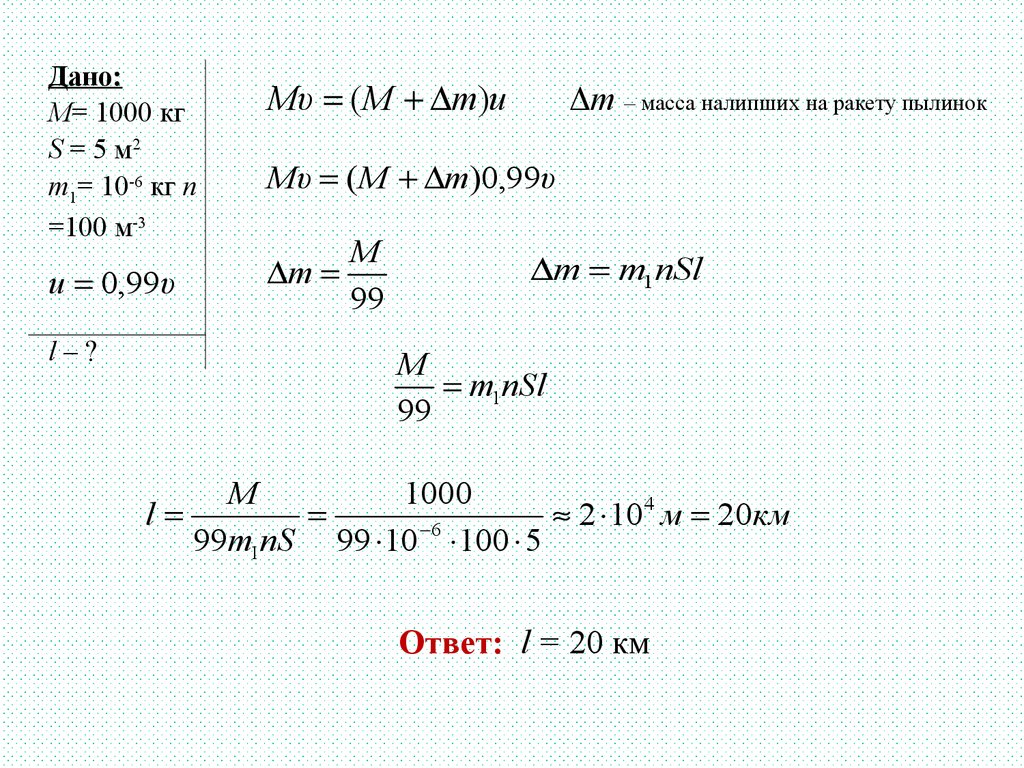
Ракета массой 1 тонна с поперечным сечением 5 м2летела с выключенным двигателем и попала в
облако пыли. Масса каждой пылинки 1 мг. Их
концентрация 100 м-3, соударения с ракетой
абсолютно неупругие. Какова длина облака, если
после пролета через него ракета потеряла 1 %
скорости?
(Трофимова Е.В., Шишкина А.Ф. Задачи повышенной
сложности по общей физике, Уфа, 2015)
5.
Дано:M= 1000 кг
S = 5 м2
m1= 10-6 кг n
=100 м-3
u 0,99υ
l–?
Mυ ( M m)u
Δm – масса налипших на ракету пылинок
Mυ ( M m)0,99υ
m
M
99
m m1nSl
M
m1nSl
99
M
1000
4
l
2
10
м 20км
6
99m1nS 99 10 100 5
Ответ: l = 20 км
6. Задача 3
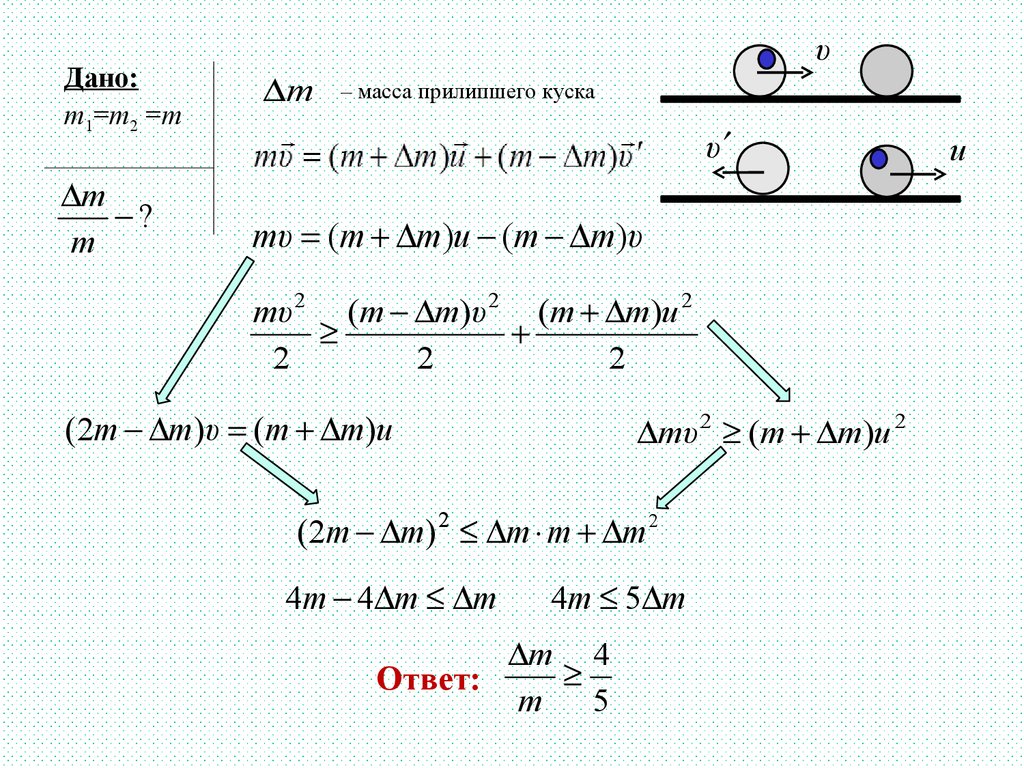
Сталкиваются два тела одинаковой массы, одно изкоторых неподвижно. При ударе часть движущегося
тела прилипает к неподвижному, а остальная часть
отскакивает назад со скоростью, равной по величине
скорости до столкновения. При каких отношениях
массы прилипшей части тела к его полной массе это
возможно? Известно, что при ударе внутренняя
энергия тел не увеличивается.
(Трофимова Е.В., Шишкина А.Ф. Задачи повышенной
сложности по общей физике, Уфа, 2015)
7.
Дано:m1=m2 =m
m
?
m
υ
m
– масса прилипшего куска
υ
mυ (m m)u (m m)υ
mυ 2 (m m)υ 2 (m m)u 2
2
2
2
(2m m)υ (m m)u
mυ 2 (m m)u 2
(2m m) 2 m m m 2
4m 4 m m
4m 5 m
m 4
Ответ:
m
5
u
8. Задача 4
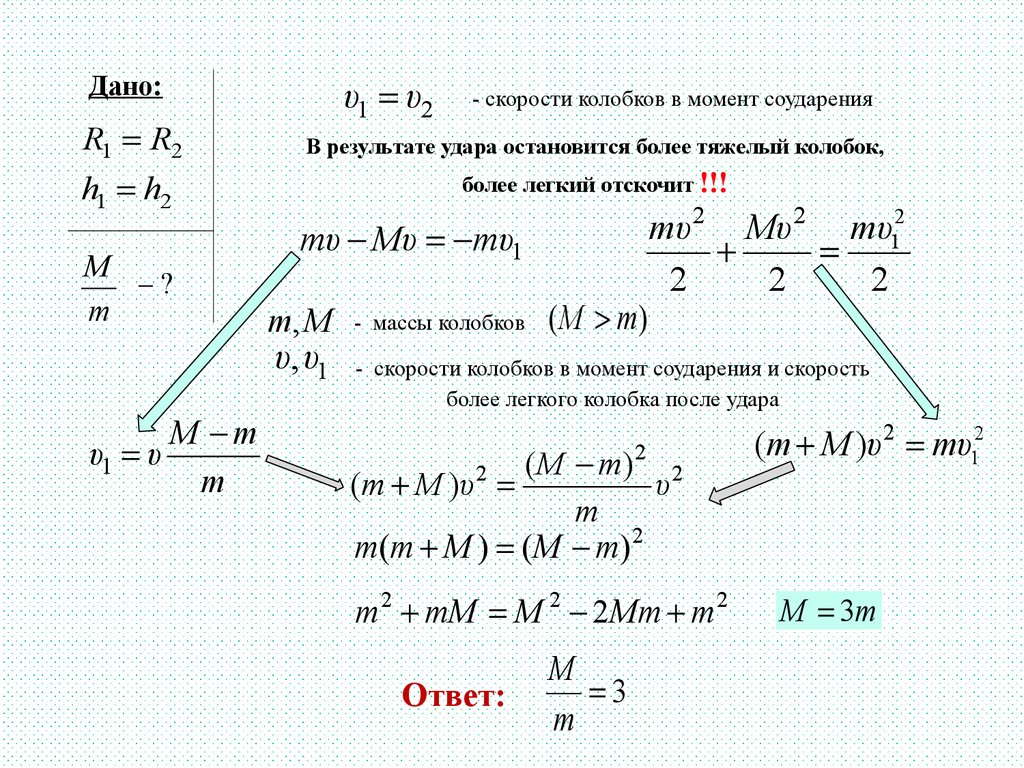
Два колобка одинакового размера, но разных масс, незамечая вокруг себя ничего, соскальзывают навстречу
друг другу с горок одинаковой высоты и у их
основания сталкиваются лоб в лоб. Определите
отношение масс колобков, если в результате
столкновения один из колобков остановился.
Соударение колобков считать абсолютно упругим.
Трения нет.
(Всероссийская аэрокосмическая олимпиада, 9 кл, 2015 г.)
9.
Дано:υ1 υ2
- скорости колобков в момент соударения
R1 R2
В результате удара остановится более тяжелый колобок,
h1 h2
более легкий отскочит !!!
M
–?
m
mυ Mυ mυ1
m, M
υ,υ1
M m
υ1 υ
m
- массы колобков
( M m)
mυ 2 Mυ 2 mυ12
2
2
2
- скорости колобков в момент соударения и скорость
более легкого колобка после удара
2
( M m) 2
(m M )υ
υ
m
m( m M ) ( M m ) 2
2
m 2 mM M 2 2 Mm m 2
Ответ:
M
3
m
(m M )υ 2 mυ12
M 3m
10. Задача 5
Начашу
пружинных
весов,
совершающую
гармонические
колебания
в
вертикальном
направлении, с высоты h без начальной скорости
упала бусинка и после абсолютно упругого удара о
чашу снова поднялась на ту же высоту h (рисунок).
Затем через каждую половину периода колебаний
чаши, имевших место до первого удара, ситуация стала
повторяться. Удары бусинки о чашу происходят в тот
момент, когда чаша достигает положения равновесия.
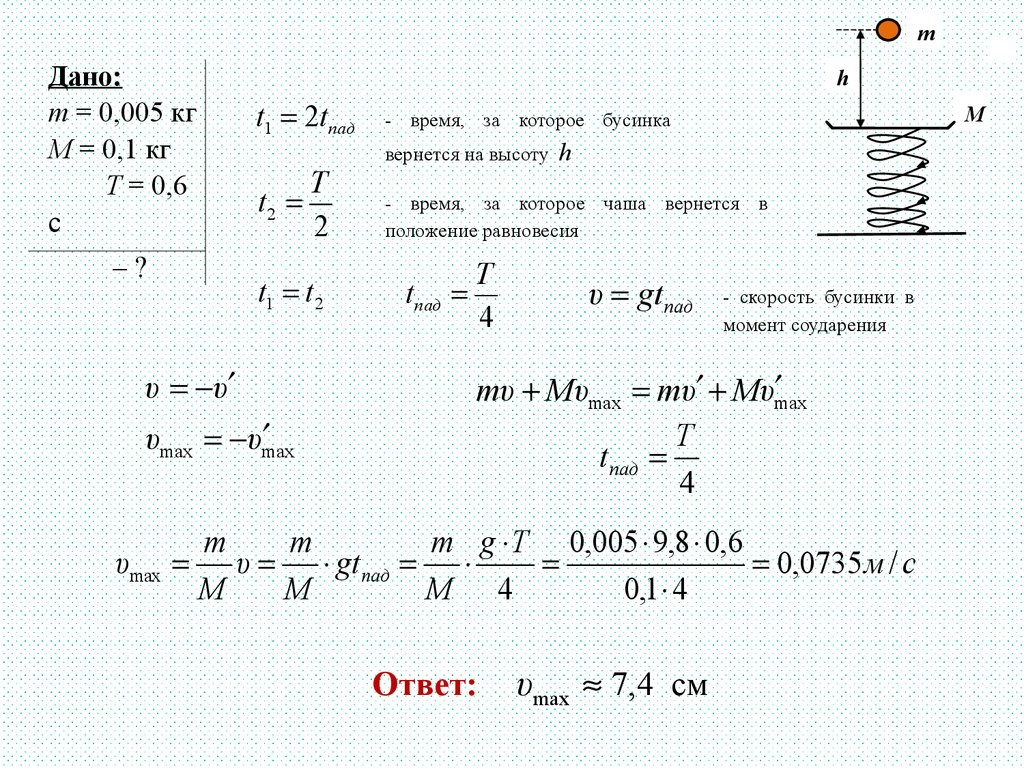
Масса бусинки в m = 5 г, масса чаши M = 100 г. Период
свободных колебаний чаши Т = 0,6 с. Определите
скорость чаши в момент удара бусинки.
(Всероссийская аэрокосмическая олимпиада, 2014 г.)
m
h
M
11.
mДано:
m = 0,005 кг
M = 0,1 кг
Т = 0,6
с
–?
h
t1 2t пад
вернется на высоту
Т
t2
2
t1 t 2
υ υ
υmax υmax
υmax
M
- время, за которое бусинка
h
- время, за которое чаша вернется в
положение равновесия
t пад
Т
4
υ gt пад
- скорость бусинки в
момент соударения
mυ Mυmax mυ Mυ max
Т
t пад
4
m
m
m g Т 0,005 9,8 0,6
υ gtпад
0,0735 м / с
M
M
M 4
0,1 4
Ответ:
υmax 7,4 см
12. Задача 6
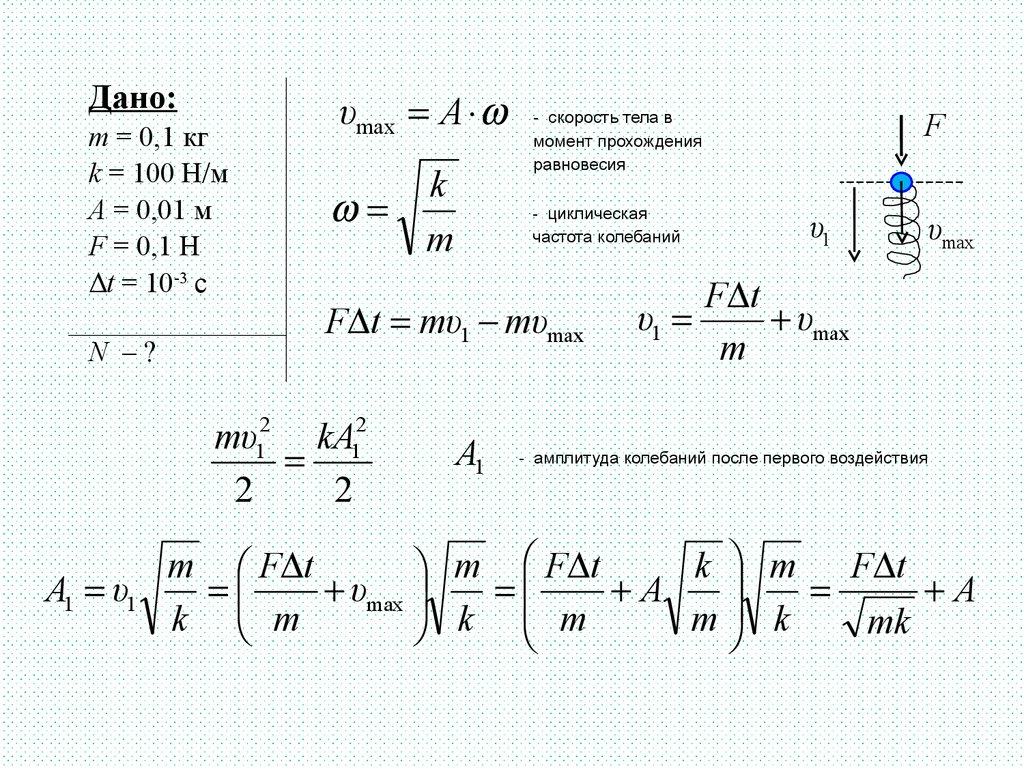
Небольшое тело массой m = 100 г совершает малыевертикальные гармонические колебания на пружине
жесткостью k = 100 Н/м с амплитудой А = 1 см. В тот
момент, когда тело при движении вниз проходит
положение равновесия, на него воздействуют внешней
силой F = 0,1 Н в течение времени Δt = 10-3 с,
направленной вертикально вниз. Определите амплитуду
колебаний после N = 2013 таких воздействий. Колебания
остаются гармоническими.
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
13.
Дано:m = 0,1 кг
k = 100 Н/м
A = 0,01 м
F = 0,1 Н
Δt = 10-3 с
N –?
υmax A
k
m
A1 υ1
- циклическая
частота колебаний
F t mυ1 mυmax
mυ12 kA12
2
2
A1
F
- скорость тела в
момент прохождения
равновесия
υ1
υmax
F t
υ1
υmax
m
- амплитуда колебаний после первого воздействия
m F t
k m F t
m F t
υmax
A
A
k m
m k
mk
k m
14.
F t mυ2 mυ1A2 υ2
F t
υ2
υ1
m
mυ22 kA22
2
2
m F t
m F t
m
υ1
2
υmax
k m
k m
k
F t
k m
F t
2
A
2
A
m k
mk
m
После N воздействий :
F t
0,1 10 3
AN N
A 2013
0,01 0,074( м)
mk
0,1 100
Ответ:
AN 7,4 см
15. Задача 7
В длинном прямом горизонтальном желобе нарасстояниях l = 1 см друг от друга лежат n = 2011
маленьких шариков. Шарики расположены в порядке
убывания их масс. Массы соседних шариков
отличаются друг от друга на α = 1%. Самому тяжелому
шарику сообщили скорость υ1 = 1 см/с в направлении
остальных шариков. Считая все удары упругими и
центральными, найдите время, через которое начнет
двигаться самый легкий шарик. Трения нет. Временем
соударения шариков друг с другом пренебречь.
(Всероссийская аэрокосмическая олимпиада, 2011 г.)
16.
Дано:l = 0,01 см
n = 2011
α = 0,01
= 0,01 м/с
υ1
tN – ?
Шарики расположены в порядке убывания масс
после соударения любой из налетающих шариков будет
двигаться в первоначальном направлении
m1 m
m2 (1 )m
m3 (1 ) 2 m
...
- масса первого шарика
- масса второго шарика
- масса третьего шарика
mN (1 ) N m
Первое соударение
mυ1 mu (1 )m
mυ12 mu 2 (1 )mυ22
2
2
2
u – скорость первого шарика после соударения
υ2 – скорость второго шарика после соударения
17.
u υ1 (1 )υ2υ1 υ1 (1 )υ2 (1 )υ22
2
2
υ2
υ1
2
Скорости третьего, четвертого и т.д. шариков после соударений
2
2
υ3
υ1
2
3
2
2
...
υ4
υ2010
υ1
2
2
Время между соударениями i-го и (i+1) шариков
ti ,i 1
l
υi
l 2
υ1 2
i 1,2,3...2010
2009
i 1
υ1
18.
Время, через которое начет двигаться 2011-й шарик :l l l
l
l l 2 l 2
t N ...
υ1 υ2 υ3
υ2010 υ1 υ1 2 υ1 2
2 2010
1
l
2
tN
2
υ1
1
2
2
l 2
...
υ1 2
2010
2l 2
1
υ1 2
2010
2 0,01 2 0,01
tN
1
200c
0,01 0,01 2
Ответ:
t N = 200 с
2009
19. Задача 8
На гладкой горизонтальной поверхности вдоль однойпрямой на равных расстояниях l = 1 см друг от друга
расположены 2011 брусков массой m = 10 г каждый (см.
рисунок). К первому бруску приложили постоянную
горизонтальную силу F = 1 Н в направлении остальных
брусков. Определите скорости брусков после последнего
соударения. Соударения брусков абсолютно неупругие.
(Всероссийская аэрокосмическая олимпиада, 2011 г.)
l
l
m
m
m
...
m
20.
FДано:
l= 0,01 м
N = 2011
m = 0,01 кг
F=1Н
υ2010 – ?
A F l
l
l
m
m
m
...
m
- работа силы F на пути l между соударениями
mυ12
0 F l
2
- изменение механической энергии 1-го бруска от
начала движения до соударения со 2-м бруском
2F l
υ1
m
mυ1 2mυ2
mυ1 2mυ2
1
1 2F l 1 F l
υ2 υ1
2
2 m
2 2m
2mu22 2mυ22
F l
2
2
- от первого соударения до соударения с 3-м бруском
2F l 2
F l F l
3F l
u2
υ
2
m
m 2m
2m
- скорость 1+2 бруска перед соударением с 3-м
21.
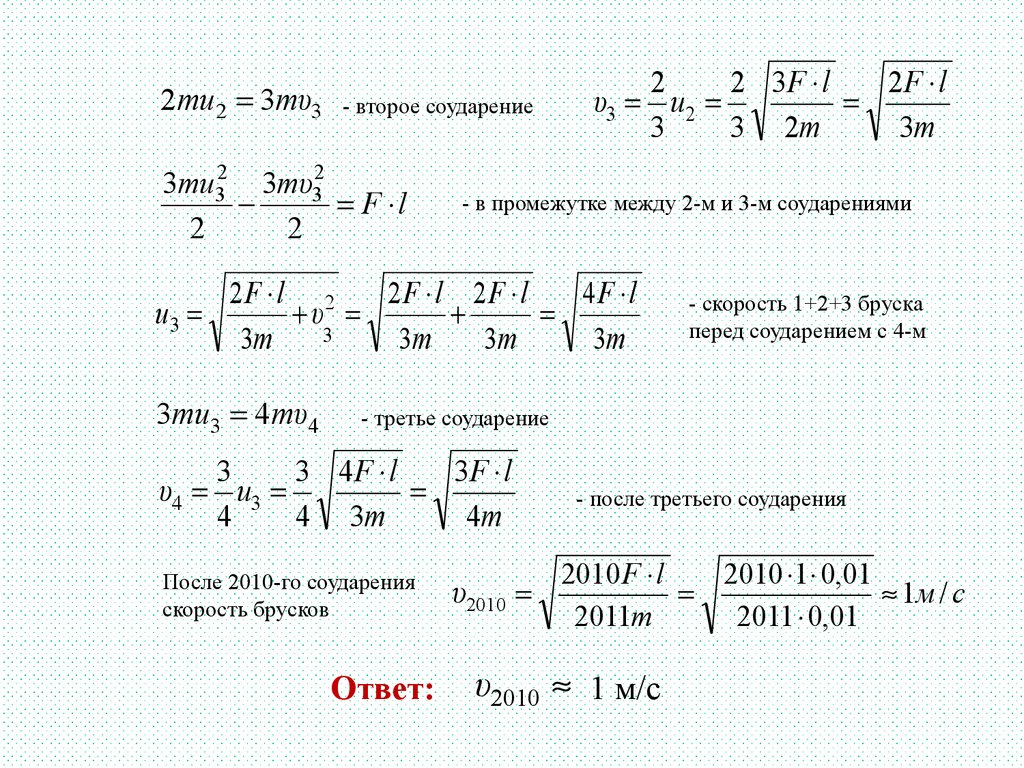
2mu2 3mυ3- второе соударение
3mu32 3mυ32
F l
2
2
u3
2
2 3F l
2F l
υ3 u2
3
3 2m
3m
- в промежутке между 2-м и 3-м соударениями
2F l 2
2F l 2F l
4F l
υ
3
3m
3m
3m
3m
3mu3 4mυ4
- скорость 1+2+3 бруска
перед соударением с 4-м
- третье соударение
3
3 4F l
3F l
υ4 u3
4
4 3m
4m
После 2010-го соударения
скорость брусков
Ответ:
υ2010
- после третьего соударения
2010 F l
2010 1 0,01
1м / с
2011m
2011 0,01
υ2010 1 м/с
22. Задача 9
Маленькийшарик
подвешен
на
невесомой
нерастяжимой нити, прикрепленной к вертикальной
стене. Нить с шариком отклоняют в плоскости,
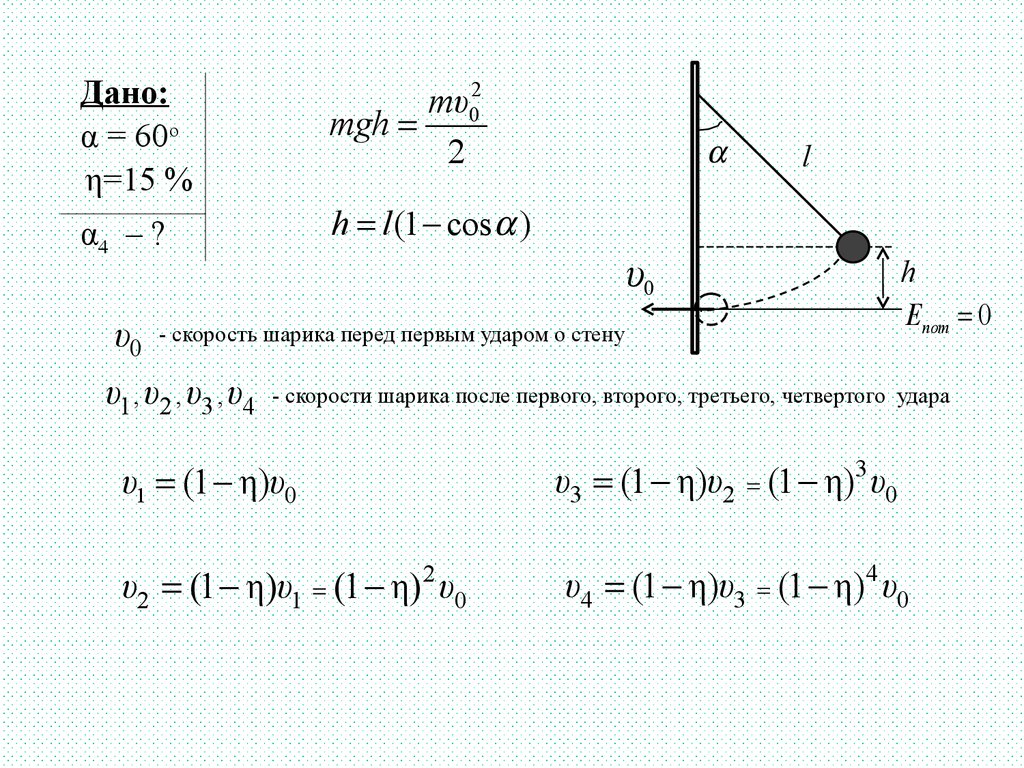
перпендикулярной стене, на угол α = 60о от вертикали (см
рисунок) и отпускают без начальной скорости. Шарик
совершает колебательные движения, периодически
ударяясь о стену. При каждом ударе шарик теряет η=15
% скорости, и угол отклонения нити постепенно
уменьшается. Каким будет максимальный угол
отклонения нити после четвертого удара шарика о
стенку?
(Всероссийская аэрокосмическая олимпиада, 10 кл, 2015 г.)
23.
Дано:α = 60о
η=15 %
mυ02
mgh
2
α4 – ?
h l (1 cos )
υ0
l
υ0
- скорость шарика перед первым ударом о стену
υ1 , υ2 , υ3 , υ4
h
Епот 0
- скорости шарика после первого, второго, третьего, четвертого удара
υ1 (1 η)υ0
υ3 (1 η)υ2 (1 η)3 υ0
υ2 (1 η)υ1 (1 η) 2 υ0
υ4 (1 η)υ3 (1 η) 4 υ0
24.
mυ42mgl (1 cos 4 )
2
m(1 η)8 υ02
mgl (1 cos 4 )
2
(1 η)8 mgl (1 cos ) mgl (1 cos 4 )
cos 4 1 (1 η)8 (1 cos ) 1 (1 0,15)8 (1 cos 60o ) 0,8638
4 arccos 0,8638 30o
Ответ:
4 30o
25. Задача 10
Маленькийшарик
подвешен
на
невесомой
нерастяжимой нити вблизи вертикальной стены. Нить с
шариком отклоняют в плоскости, параллельной стене,
на угол α = 60о от вертикали и отпускают без начальной
скорости. На каком расстоянии от точки подвеса прямо
под ней следует забить в стену гвоздь, чтобы шарик,
зацепившись нитью за гвоздь, поднялся до высшей
точки своей траектории на натянутой нити (сделал один
оборот вокруг гвоздя? Длина нити l = 50 см.
(Всероссийская аэрокосмическая олимпиада, 2015 г.)
26.
Дано:α = 30о
l = 0,5 м
Т
mg
R l х
υ
l
- радиус окружности, по которой
двигается шарик после соударения
х–?
h
l х
mυ 2
mgh
mg 2(l х)
2
h l (1 cos )
υ2
m T mg
R
Епот 0
υ
- скорость в верхней точке траектории
υ 2 2 gl (1 cos ) 4 g (l х)
2 gl (1 cos ) 4 g (l х)
m
T mg
l х
27.
Т m2 gl (1 cos ) 4 g (l х)
mg
l х
>0
: mg
2l (1 cos ) 4(l х) (l х)
1
1
х l (3 2 cos ) 0,5(3 2 cos 600 ) 0,4 м
5
5
Ответ:
х = 40 cм
28. Задачи для самостоятельного решения
Задача 1. Груз математического маятника отвели нанатянутой нити до горизонтального положения и
отпустили без начальной скорости. В момент
прохождения равновесия скорость груза равнялась
некоторому значению υ . Сможет ли этот груз совершить
полный оборот в вертикальной плоскости, если ему в
положении равновесия сообщить горизонтальную
скорость 1,5υ ? Ответ обосновать.
Ответ: Не сможет
29.
Задача 2. Тело массы m = 1 кг скользит без тренияпо гладкому горизонтальному столу и въезжает
на подвижную горку массы М = 5 кг. Высота
горки Н = 1,2 м. Трение между столом и горкой
отсутствует. Найти конечные скорости тела и
горки. Начальная скорость тела υ0 5 м/с.
(Трофимова Е.В., Шишкина А.Ф. Задачи повышенной
сложности по общей физике, Уфа, 2015)
Ответ: 3,33 м/и 1,67 м/с
30.
Задача 3. Три поросенка Ниф-ниф, Наф-наф и Нуф-нуфлепят снеговика в виде трех шаров, радиусы которых
относятся как 3:2:1. Затем эти шары устанавливаются
друг на друга так, чтобы их центры находились на
одной вертикали. При этом Ниф-ниф делает самый
большой шар, Наф-наф делает и устанавливает на
место средний шар, а Нуф-нуф делает и устанавливает
маленький шар. Какую часть от всей работы,
затраченной на изготовление снеговика, выполнил
каждый поросенок? Снег считать однородным.
(Всероссийская аэрокосмическая олимпиада, 2011 г.)
81
64
11
, 2
, 3
Ответ: 1
156
156
156
31. rabtchuk_ludmila@mail.ru
Благодарю за внимание !rabtchuk_ludmila@mail.ru















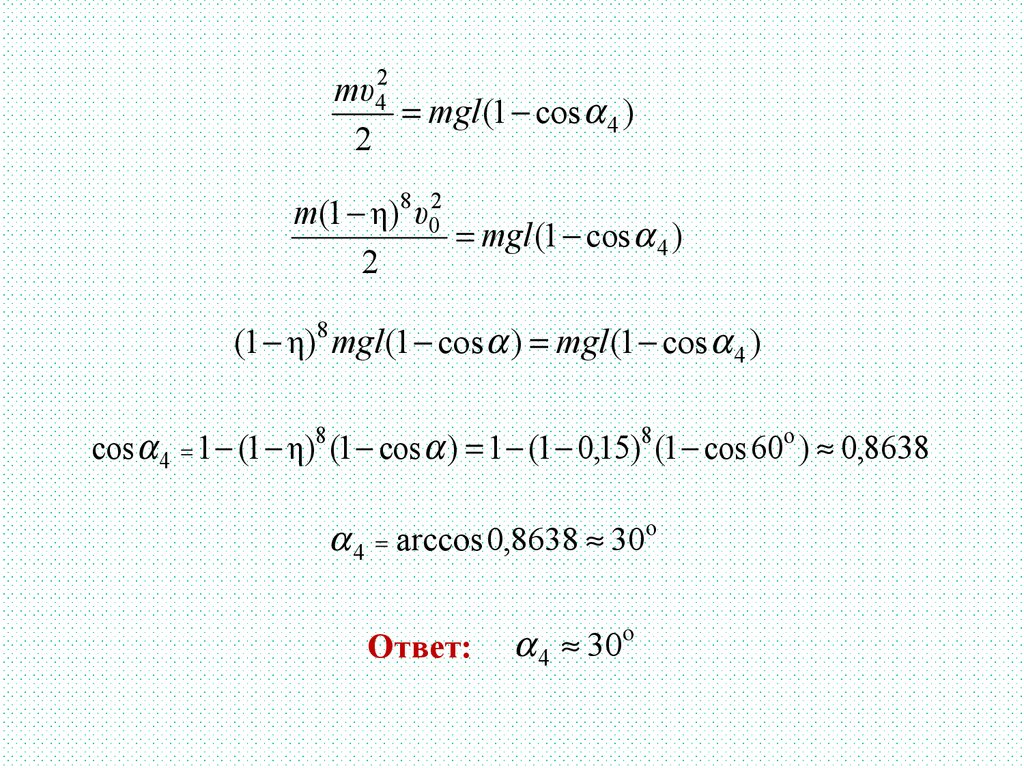







 mathematics
mathematics physics
physics








