Similar presentations:
Лекция 5: Волновая оптика. Оптика световых пучков. Оптические резонаторы
1. Лекция 5: Волновая оптика Оптика световых пучков Оптические резонаторы
2. Оптические пучки
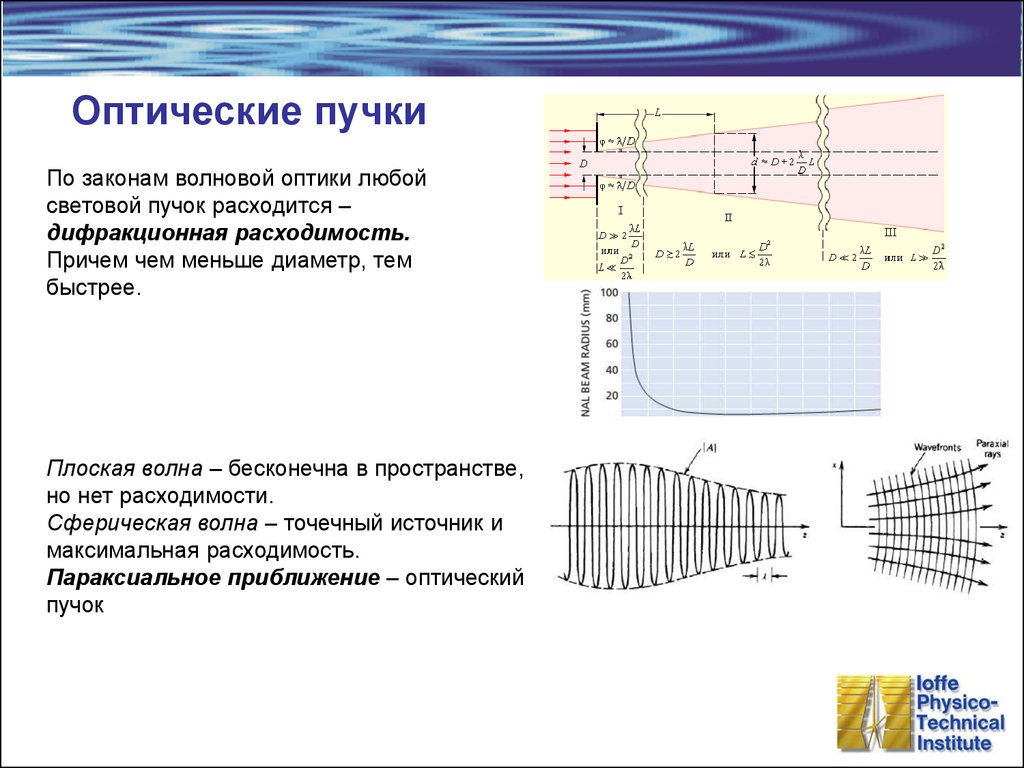
По законам волновой оптики любойсветовой пучок расходится –
дифракционная расходимость.
Причем чем меньше диаметр, тем
быстрее.
Плоская волна – бесконечна в пространстве,
но нет расходимости.
Сферическая волна – точечный источник и
максимальная расходимость.
Параксиальное приближение – оптический
пучок
3. Гауссов пучок (излучение лазера)
Решение волнового уравнения Гельмгольца для монохроматической волны впараксиальном приближении
U r A r exp jkz ;
2U r k 2U r 0 T A r j 2k
2
A r
0
z
Сферическая волна в параксиальном приближении дает параболическую волну,
Гауссов пучок другое решение с квадратичной зависимость фазового фронта.
A1
x2 y 2
A r
exp jk
z jz0
2
z
jz
0
R(L)
Параметры A0= A1/jz0 и z0 определяются из граничных условий
4. Свойства Гауссова пучка
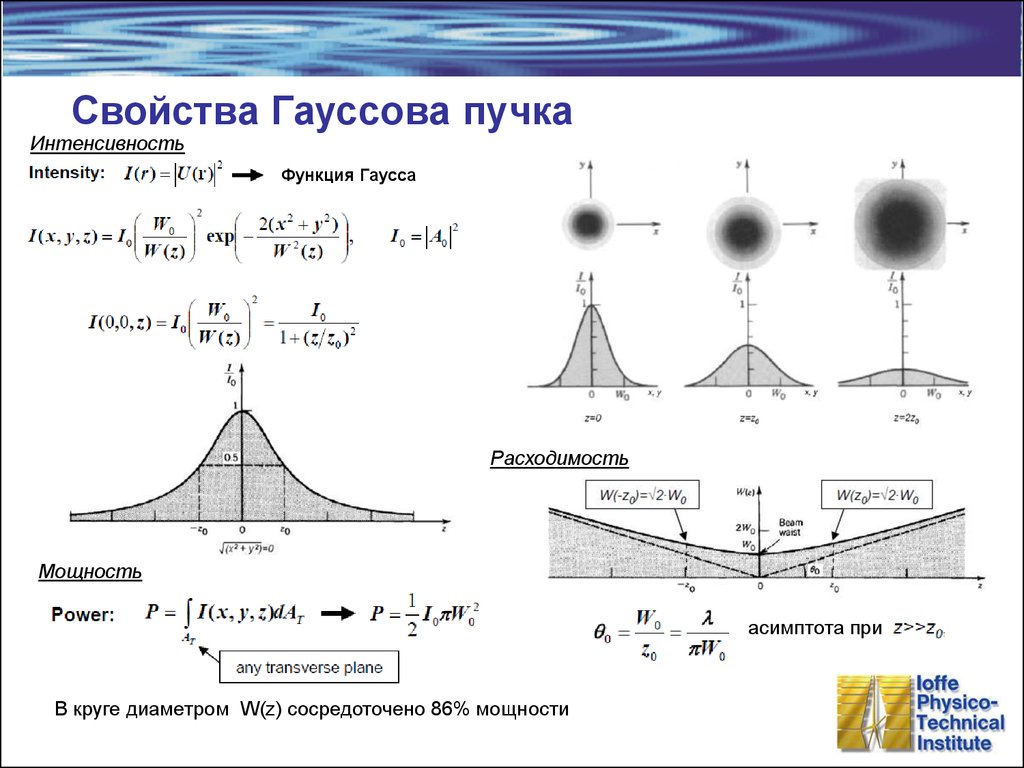
ИнтенсивностьФункция Гаусса
Расходимость
Мощность
асимптота при
В круге диаметром W(z) сосредоточено 86% мощности
5. Свойства Гауссова пучка
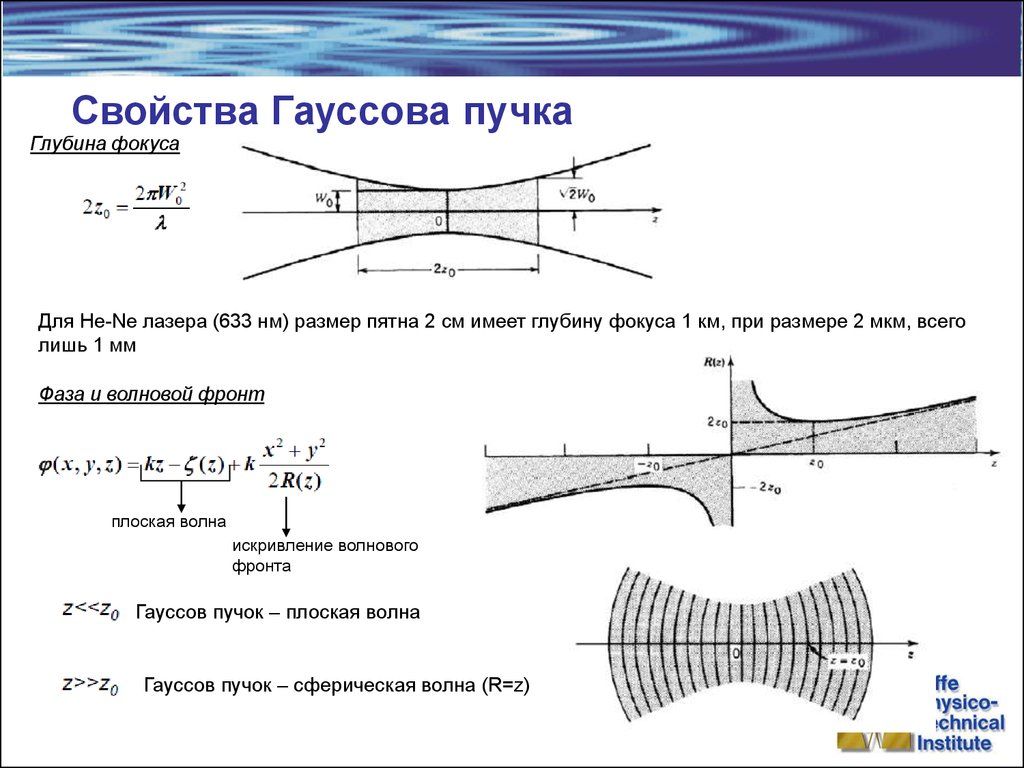
Глубина фокусаДля He-Ne лазера (633 нм) размер пятна 2 см имеет глубину фокуса 1 км, при размере 2 мкм, всего
лишь 1 мм
Фаза и волновой фронт
плоская волна
искривление волнового
фронта
Гауссов пучок – плоская волна
Гауссов пучок – сферическая волна (R=z)
6. Прохождение Гауссова пучка через оптическую систему
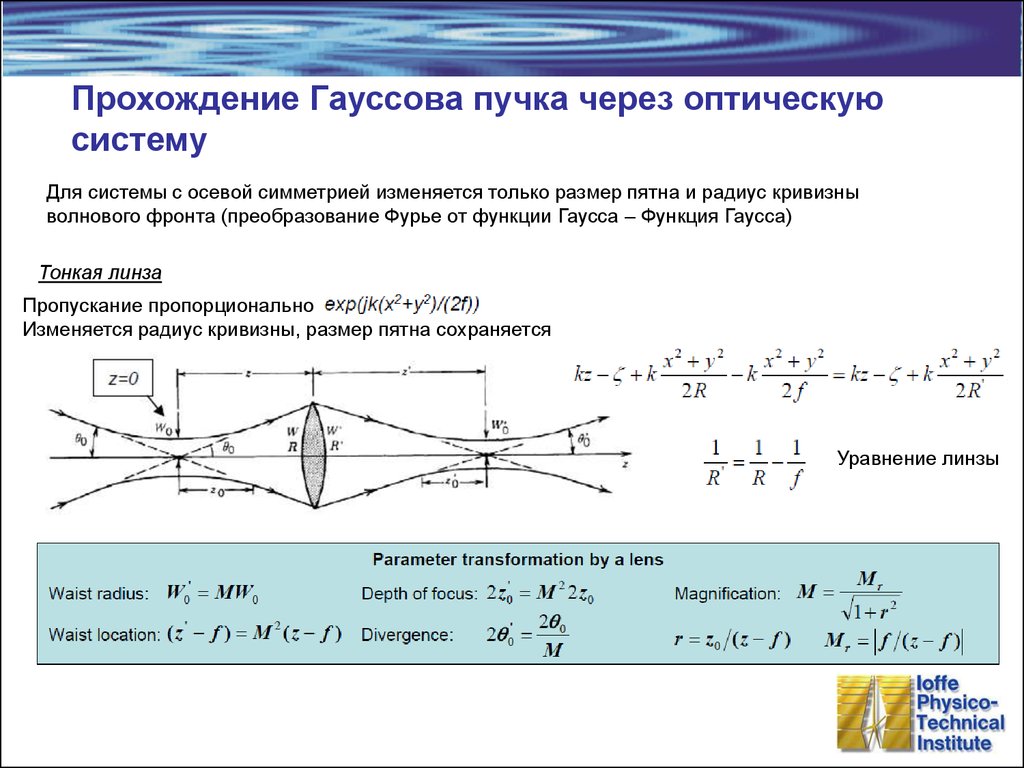
Для системы с осевой симметрией изменяется только размер пятна и радиус кривизныволнового фронта (преобразование Фурье от функции Гаусса – Функция Гаусса)
Тонкая линза
Пропускание пропорционально
Изменяется радиус кривизны, размер пятна сохраняется
Уравнение линзы
7. Прохождение Гауссова пучка через оптическую систему
Предел лучевой оптикиФокусировка
Линза располагается в перетяжке гауссова
пучка
Задержка
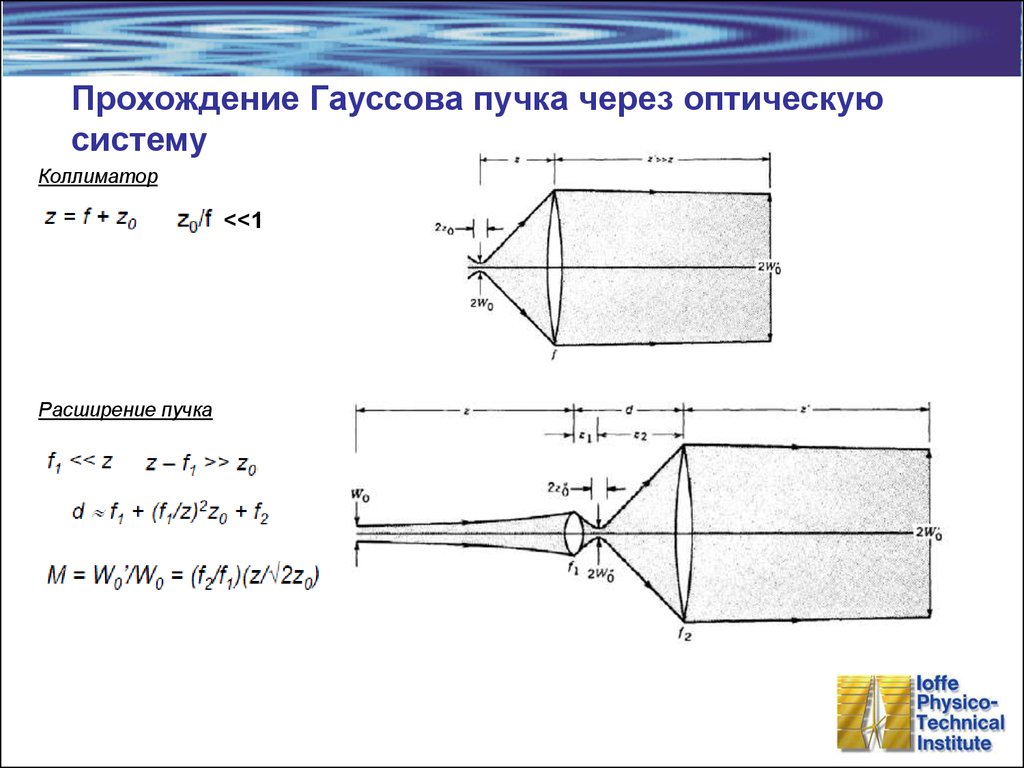
8. Прохождение Гауссова пучка через оптическую систему
Коллиматор<<1
Расширение пучка
9. Другие решения уравнения Гельмгольца в параксиальном приближении
Все функции имеют параболический фронт с одинаковым радиусом кривизны10. Оптические резонаторы
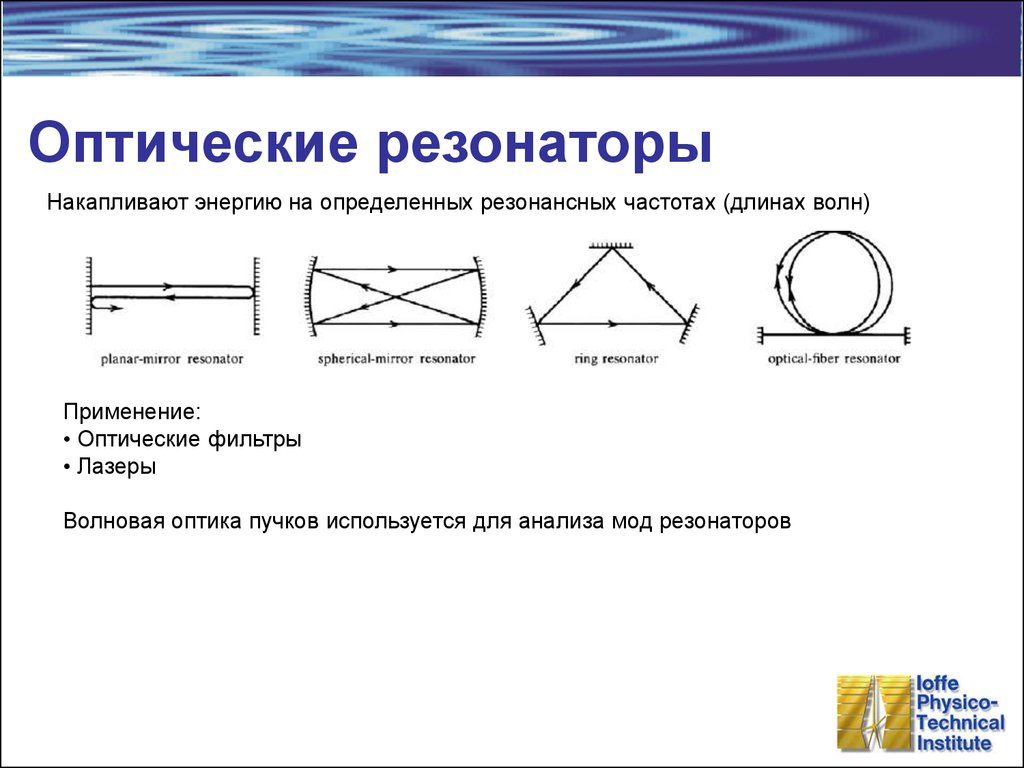
Накапливают энергию на определенных резонансных частотах (длинах волн)Применение:
• Оптические фильтры
• Лазеры
Волновая оптика пучков используется для анализа мод резонаторов
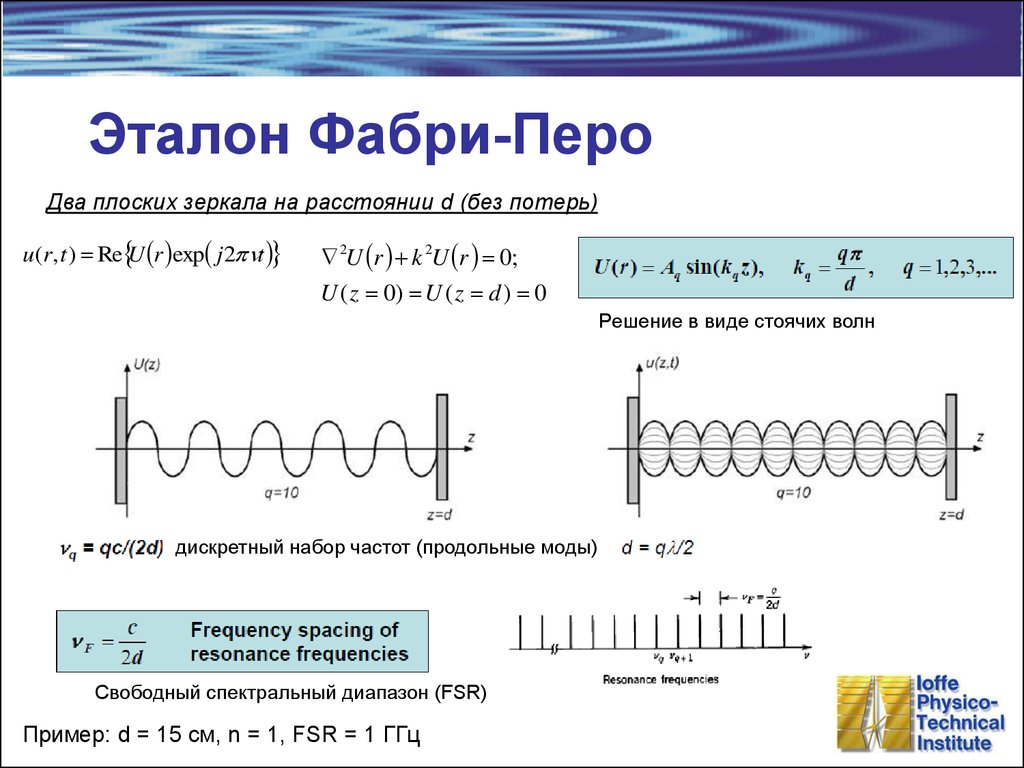
11. Эталон Фабри-Перо
Два плоских зеркала на расстоянии d (без потерь)u(r, t ) Re U r exp j 2 t
2U r k 2U r 0;
U ( z 0) U ( z d ) 0
Решение в виде стоячих волн
дискретный набор частот (продольные моды)
Свободный спектральный диапазон (FSR)
Пример: d = 15 см, n = 1, FSR = 1 ГГц
12. Эталон Фабри-Перо
Продольная мода резонатора самовоспроизводится при прохождении круга13. Эталон Фабри-Перо
Потери и спектральная ширинаЗеркала имеют конечное отражение
(R<1 –коэффициент отражения по интенсивности)
Сходящаяся геометрическая прогрессия
F – параметр характеризующий добротность резонатора
14. Эталон Фабри-Перо
Потери и FВремя жизни фотонов в резонаторе
Через приведенные потери к единице длины резонатора можно выразить экспоненциальное
затухание
Соотношение неопределенности
Добротность
Обычно очень высокий
15. Резонатор как спектроанализатор
16. Резонатор Фабри-Перо со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую точность юстировкиСферические зеркала более устойчивы к рассогласованию
Для меридиальных лучей в приближении лучевой оптики
(пересекают оптическую ось)
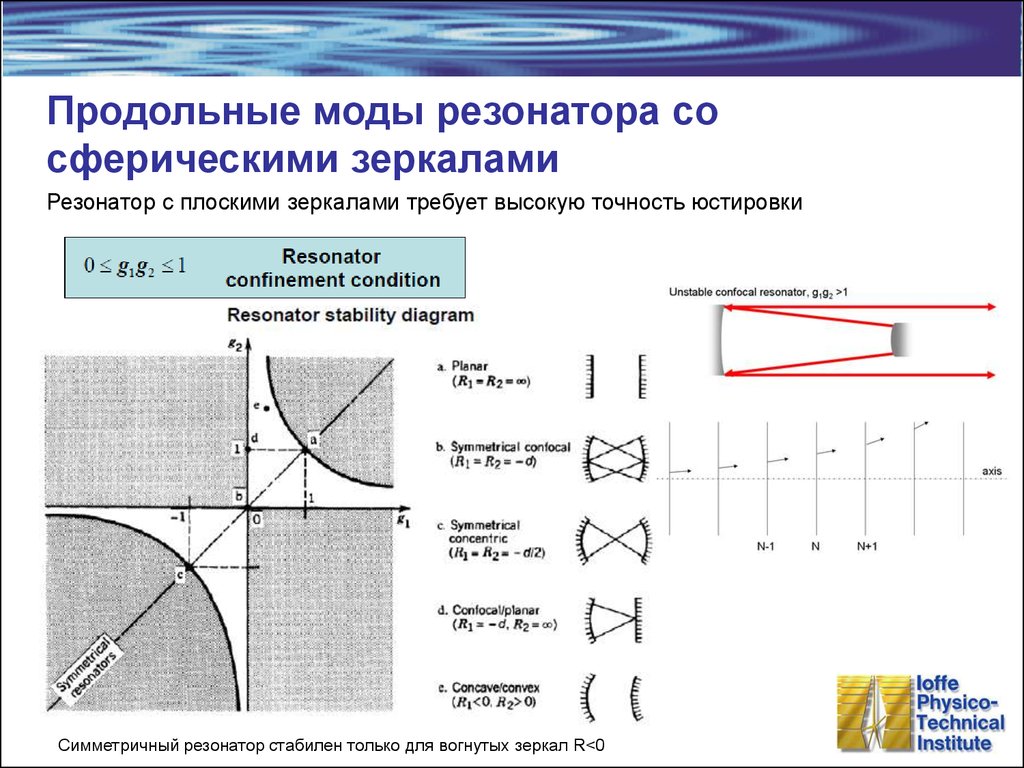
17. Продольные моды резонатора со сферическими зеркалами
Резонатор с плоскими зеркалами требует высокую точность юстировкиСимметричный резонатор стабилен только для вогнутых зеркал R<0
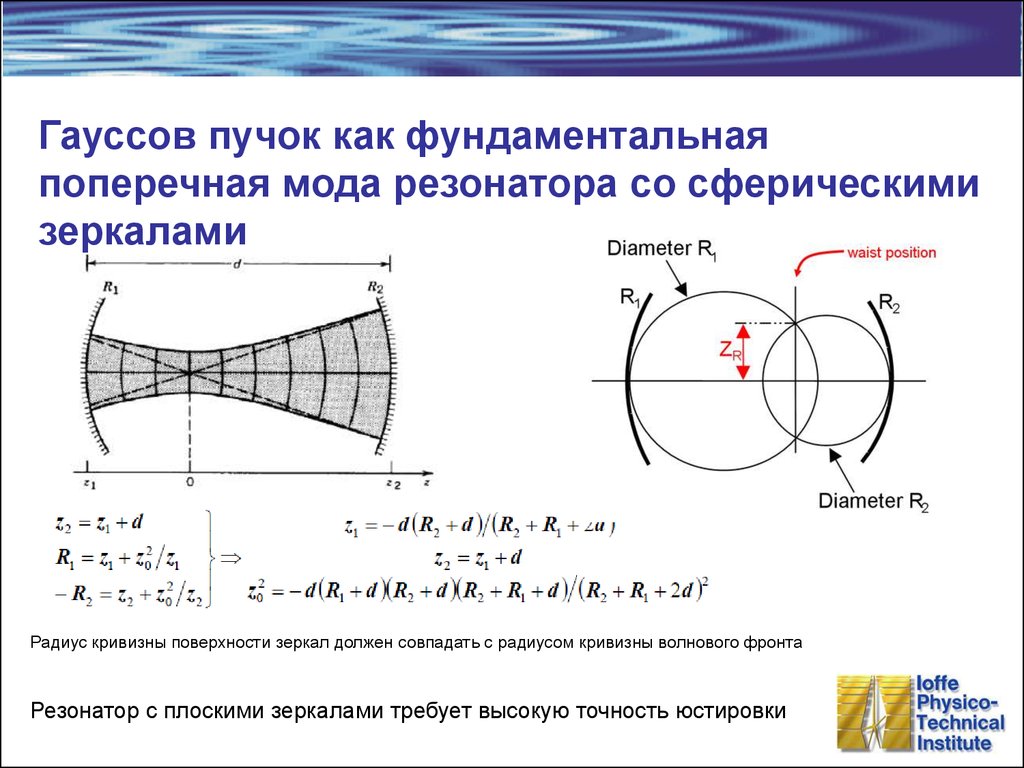
18. Гауссов пучок как фундаментальная поперечная мода резонатора со сферическими зеркалами
Радиус кривизны поверхности зеркал должен совпадать с радиусом кривизны волнового фронтаРезонатор с плоскими зеркалами требует высокую точность юстировки
19. Поперечные моды резонатора со сферическими зеркалами
Эрмитовы моды имеют тот же радиус кривизны волнового фронта, что и Гауссов пучок,поэтому тоже являются собственными модами резонатора.
Однако при прохождении резонатора различные моды будут приобретать различный набег
фазы.
Разным индексам будут соответствовать разные резонансные частоты










 physics
physics








