Взвешенные графы. Остовные деревья. Кратчайшие пути

1.

Взвешенные графы
Остовные деревья
Кратчайшие пути

2.

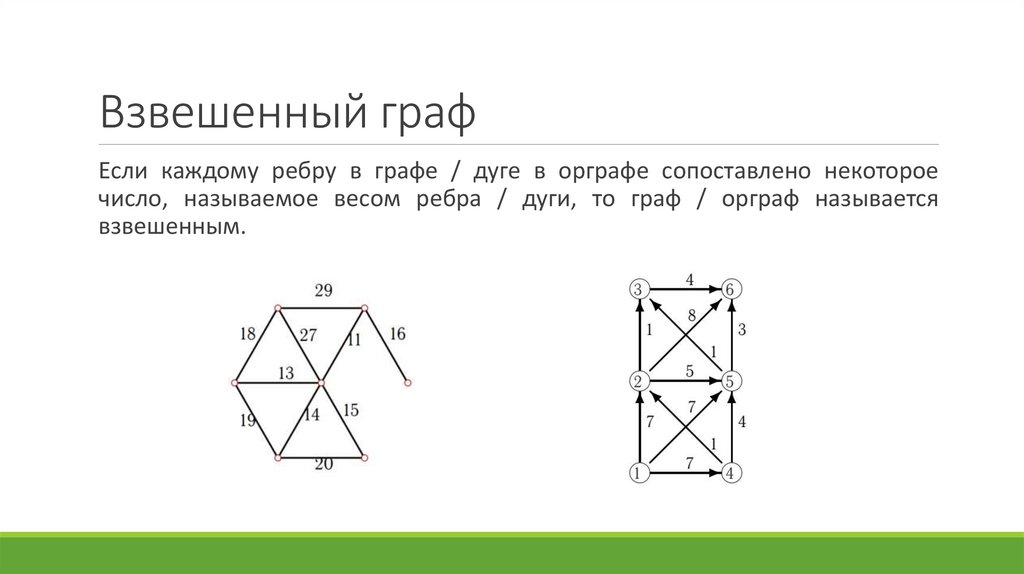
Взвешенный граф
Если каждому ребру в графе / дуге в орграфе сопоставлено некоторое
число, называемое весом ребра / дуги, то граф / орграф называется
взвешенным.

3.

Подграф
Граф, все вершины и ребра которого принадлежат исходному графу.
e12
v2
e12
v2
v1
v1
v5
e23
e25
v5
e14
e35
v3
e15
e34
e45
v4
e14
v2
e23
e45
e25
v5
e35
v3
e15
v4

4.

Остовной подграф
Остовным называется подграф, которое содержит все вершины исходного
графа.
e12
v2
e23
e25
v5
e15
e14
e35
v3
v1
e34
v2
e12
v5
e23
e45
e35
v4
v3
v1
e15
e45
v4

5.

Остовное дерево графа
Остовное дерево графа (остов) – ациклический связный подграф,
содержащий все вершины исходного графа.
Остовное дерево, у которого суммарный вес его рёбер минимален,
называется минимальным остовным деревом.
e12
v2
v1
v2
v1
e23
e25
v5
v5
e34
e15
e14
e14
e35
v3
e25
e15
e45
e35
v4
v3
v4

6.

Теорема Кирхгофа
Число остовных деревьев графа равно алгебраическому дополнению
любого элемента матрицы Кирхгофа.
Матрица Кирхгофа графа G определяется следующим образом:
−1,