Similar presentations:
Комплексные числа и квадратные уравнения
1.
Комплексные числа иквадратные уравнения.
-решение квадратных уравнений на
множестве комплексных чисел;
-алгоритм извлечения квадратного
корня из комплексного числа;
-полезные следствия для формулы
корней квадратного уравнения
2.
Квадратное уравнение сдействительными коэффициентами
?
3.
На множестве С можно находитькорни любых квадратных уравнений!
• Как извлечь квадратный корень из
отрицательных действительных чисел?
• Решение квадратных уравнений с
действительными коэффициентами и D<0.
• Как извлечь квадратный корень из любого
комплексного числа? (в алгебраической и
тригонометрической форме записи).
• Решение квадратных уравнений с комплексными
коэффициентами.
4.
Как извлечь квадратный корень изотрицательных действительных чисел?
• Определение: квадратным корнем(корнем
второй степени) из комплексного числа z
называют комплексное число, квадрат
которого равен z.
5.
Формула извлечения квадратногокорня из отрицательных
действительных чисел
6.
Решение квадратных уравнений сдействительными коэффициентами и D<0.
• Важно знать!
Если у уравнения есть комплексный корень, то и
сопряжённое ему число – тоже является корнем
этого уравнения!
Сопряжённые числа
7.
Как извлечь квадратный корень из любогокомплексного числа? (в алгебраической и
тригонометрической форме записи).
• Теорема: Если b≠0, то
Что равносильно системе условий:
8.
Например:9.
Избежать громоздких вычисленийпозволяет тригонометрическая форма
записи комплексного числа.
• Теорема:
Доказательство:
Всегда 2 корня!
10.
==
=
Аналогично:
Важно запомнить!
При возведении комплексного числа в
квадрат – его аргумент удваивается!!!
11.
Алгоритм извлечения квадратногокорня из комплексного числа:
1) Найти модуль ρ и аргумент α этого числа;
2) Провести окружность радиусом √ρ с центром
в начале координат;
3) Провести через начало координат прямую
под углом к положительному направлению
оси абсцисс;
4) Две точки пересечения проведённых
окружности и прямой – дают ответ.
12.
1).=
=
z
-2
2)-4).
-1
1
2
13.
Решение квадратных уравнений скомплексными коэффициентами.
• Так как множества
и
совпадают между
собой , то для решения квадратных уравнений
с комплексными коэффициентами можно
сохранить привычную формулу корней
квадратного уравнения:
14.
Полезные следствия для формулыкорней квадратного уравнения:
• (теорема Виета)
Если Z1 и Z –корни квадратного уравнения
2
то
• (формула разложения квадратного трёхчлена
на линейные множители)
Если Z1 и Z –корни квадратного уравнения
2
то
15.
Домашнее задание:Решить уравнение











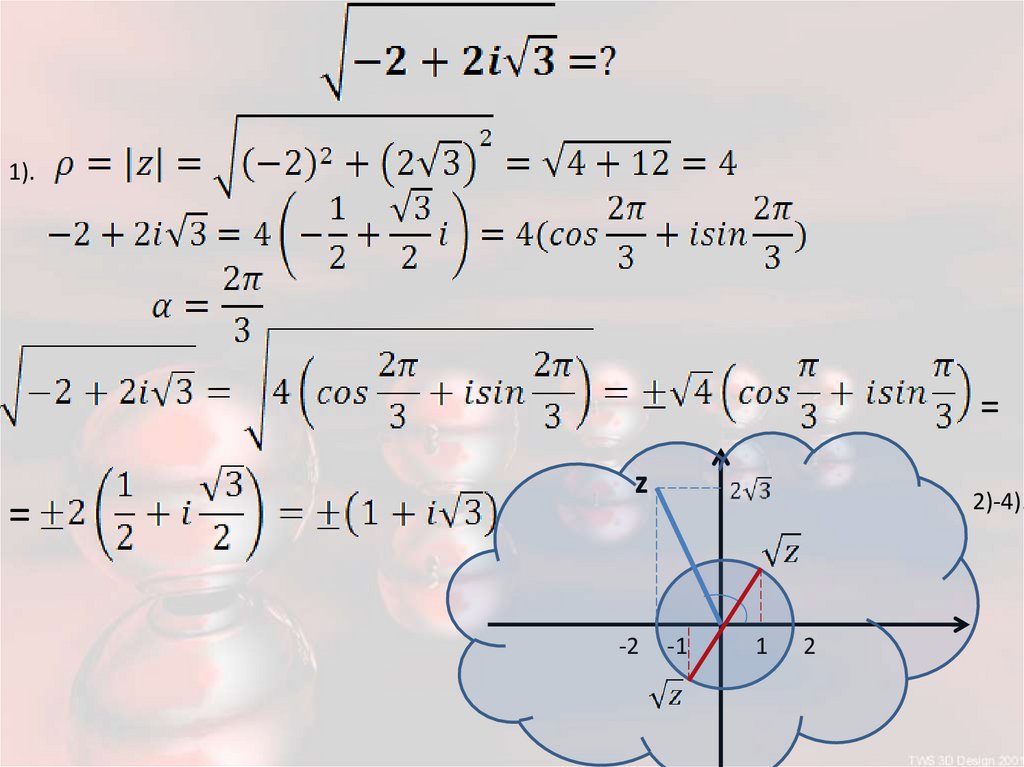



 mathematics
mathematics








