Луч и отрезок

1.

2.

Давай- те вспомним
Задача 1 : на данном луче от его начала отложить
отрезок, равный данному.
Решение.
Изобразим фигуры, данные в условии задачи: луч ОС и
отрезок АВ.
С
О
А
В
Затем циркулем построим окружность радиуса АВ с
центром О . Эта окружность пересечет луч ОС в
некоторой точке D.
D
О
Отрезок OD – искомый.
С
С

3.

Задача 2: отложить от данного луча угол, равный данному.
Решение.
Изобразим фигуры, данные в условии: угол с вершиной А
и луч ОМ.
О
М
А
Проведем окружность произвольного радиуса с центром в
вершине А данного угла. Эта окружность пересекает
стороны угла в точках В и С.
В
А
С

4.

Затем проведем окружность того же радиуса с центром в
начале данного луча ОМ. Она пересекает луч в точке D.
После этого построим окружность с центром D, радиус,
которой равен ВС. Окружности пересекаются в
E
двух точках. Одну обозначим
буквой Е. Получим угол МОЕ
D
О
М

5.

Задача 1
Построить треугольник по двум сторонам и углу между
ними.
Решение:
Прежде всего уточним, как нужно понимать эту
задачу, т. е. что здесь дано и что нужно построить.
Даны отрезки Р1Q1, Р2Q2 угол hк .
Р1
Р2
Q1
Q2
h
к

6.

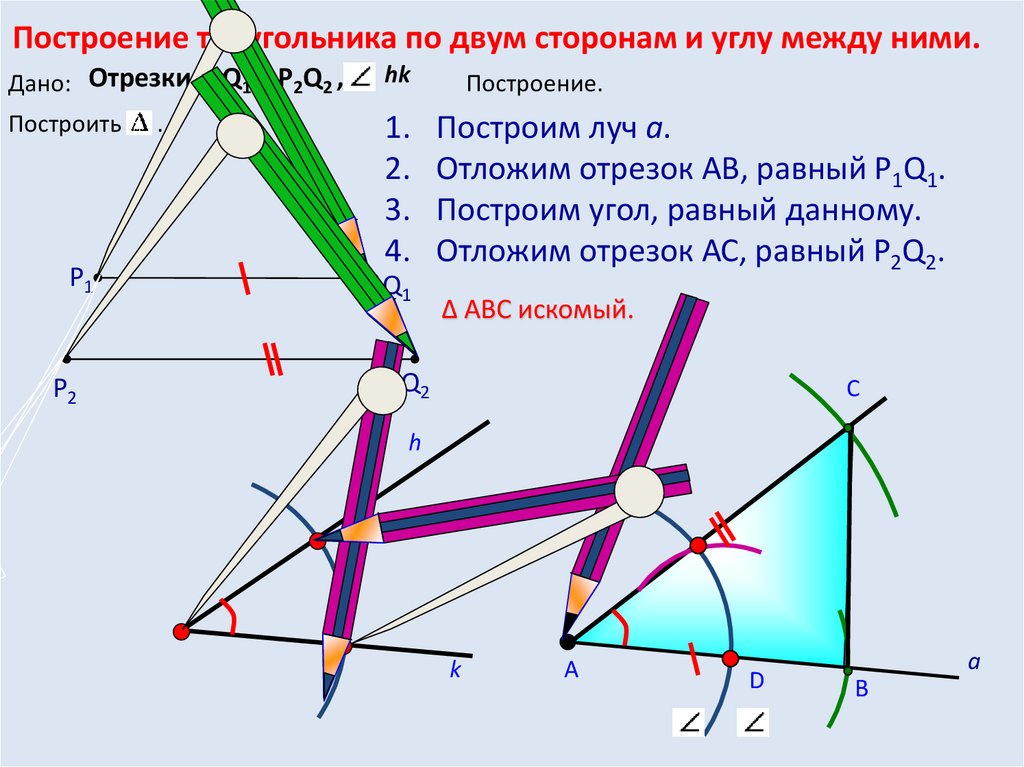
Построение треугольника по двум сторонам и углу между ними.
Дано: Отрезки Р1Q1 и Р2Q2 ,
hk
Построить
1.
2.
3.
4.
P1
P2
.
Q1
Построение.
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному.
Отложим отрезок АС, равный P2Q2.
Δ АВС искомый.
Q2
С
h
k
А
D
а
В

7.

При любых данных отрезках AB=P1Q1, AC=P2Q2 и
данном неразвернутом hk искомый треугольник
построить можно.
Так как прямую а и точку А на ней можно выбрать
произвольно, то существует бесконечно много
треугольников, удовлетворяющих условиям задачи.
Все эти треугольники равны друг другу (по первому
признаку равенства треугольников), поэтому
принято говорить, что данная задача имеет
единственное решение.

8.

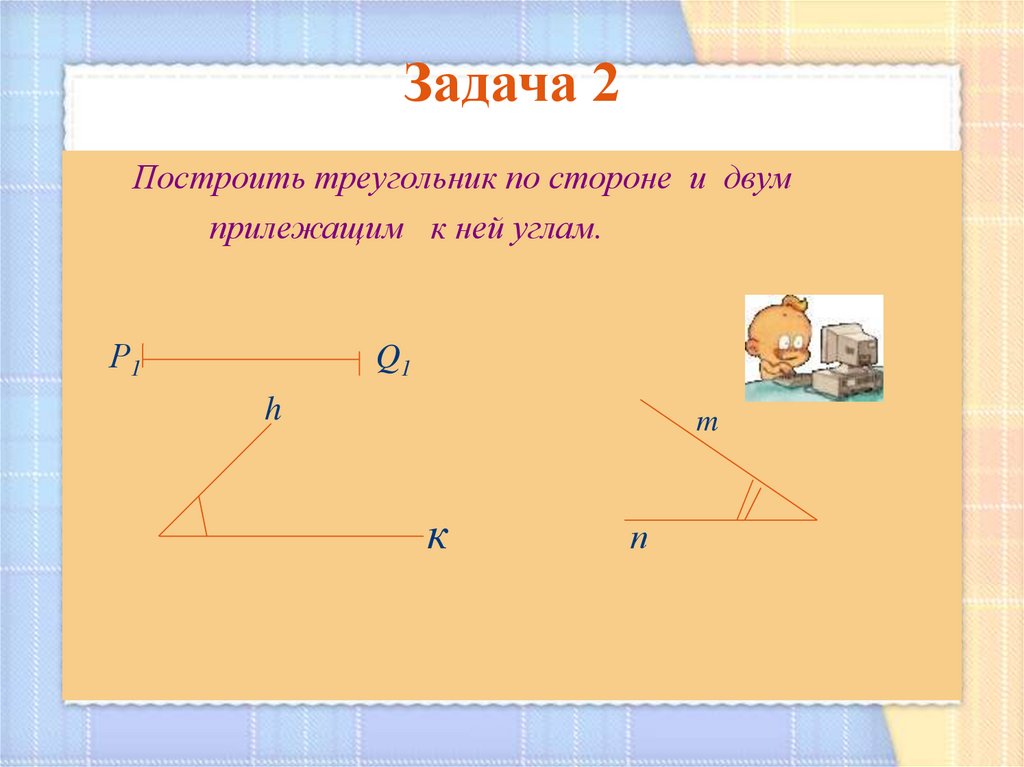
Задача 2
Построить треугольник по стороне и двум
прилежащим к ней углам.
Р1
Q1
h
m
к
п

9.

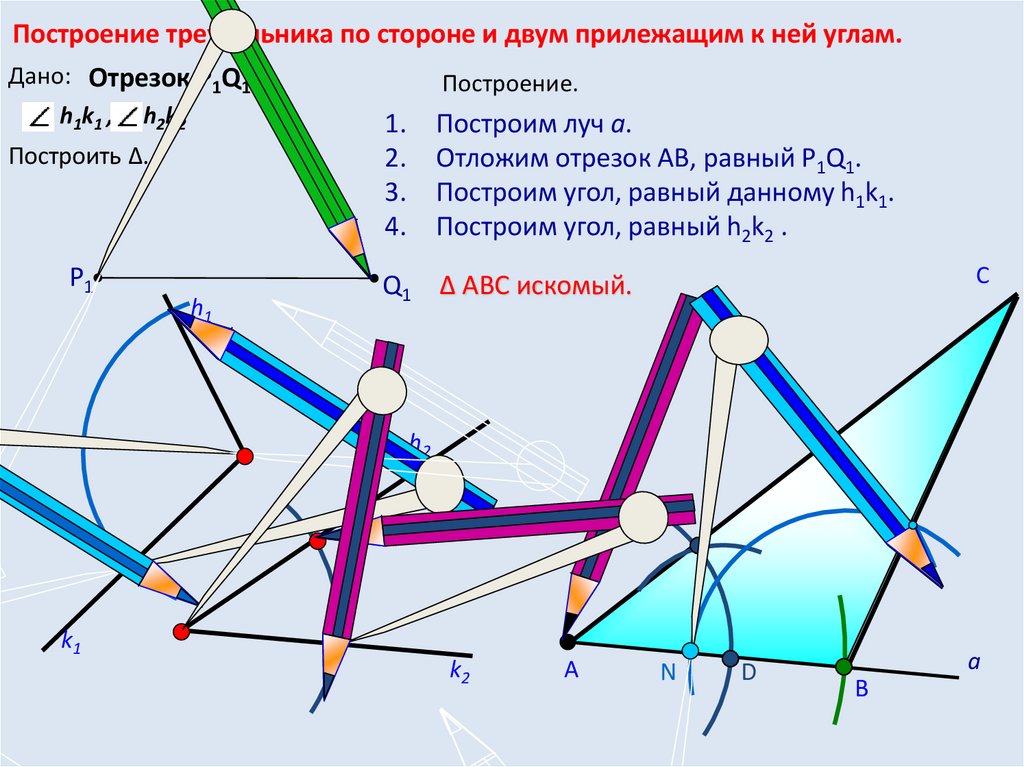
Построение треугольника по стороне и двум прилежащим к ней углам.
Дано: Отрезок Р1Q1
h1k1 , h2k2
Построить Δ.
P1
h1
Построение.
1.
2.
3.
4.
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим угол, равный данному h1k1.
Построим угол, равный h2k2 .
С
Q1 Δ АВС искомый.
h2
k1
k2
А
N
D
а
В

10.

Задача 3
Построить треугольник по трем его сторонам.
Решение.
Пусть даны отрезки Р1Q1, Р2Q2 и Р3Q3. Требуется
построить треугольник АВС, в котором
АВ = Р1Q1, AC= Р2Q2, BC= Р3Q3 .
Проведем прямую и на ней с помощью циркуля отложим
отрезок АВ, равный отрезку Р1Q1 . Затем построим две
окружности: одну — с центром А и радиусом Р2Q2.,

11.

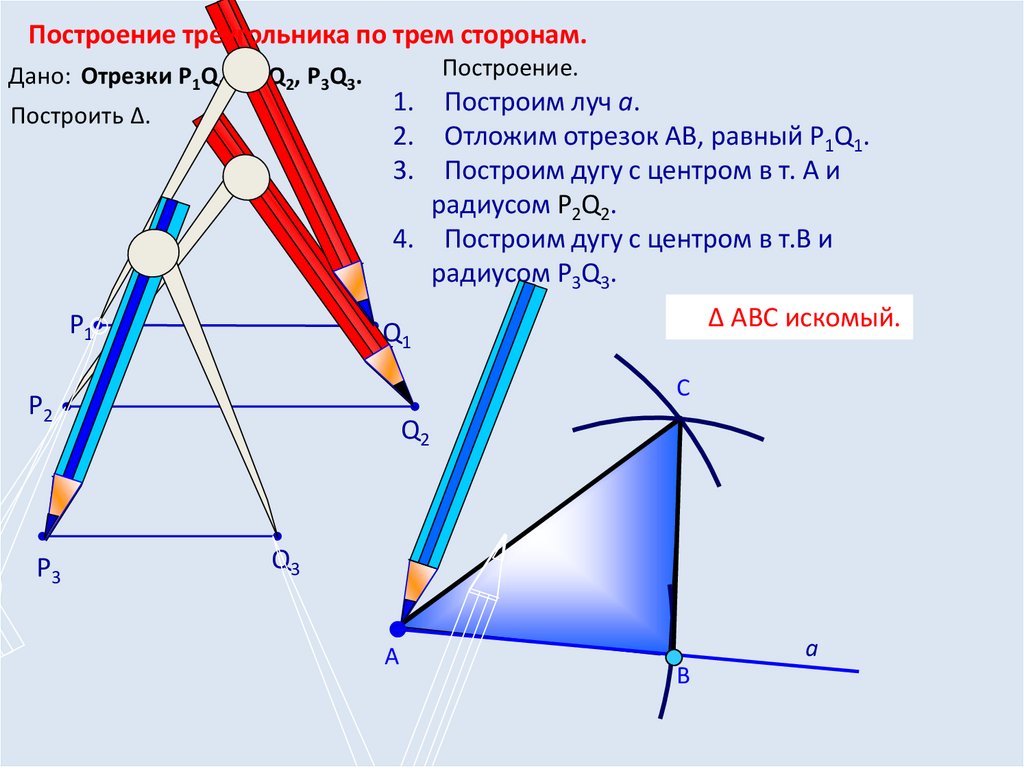
Построение треугольника по трем сторонам.
Дано: Отрезки Р1Q1, Р2Q2, P3Q3.
Построить Δ.
P1
Построение.
1.
2.
3.
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу с центром в т. А и
радиусом Р2Q2.
4. Построим дугу с центром в т.В и
радиусом P3Q3.
С
P2
P3
Δ АВС искомый.
Q1
Q2
Q3
А
а
В

12.

Задача не всегда имеет решение.
Во всяком треугольнике сумма любых двух сторон
больше третьей стороны, поэтому если какой-нибудь
из данных отрезков больше или равен сумме двух
других, то нельзя построить треугольник, стороны
которого равнялись бы данным отрезкам.

13.

Домашнее задание:
• читать пункт 39
• разобрать и записать решение
задачи № 284

14.

Какие признаки равенства
прямоугольных треугольников ты
знаешь?

15.

Теорема о соотношениях
между сторонами и углами
треугольника

16.

Признаки параллельности двух
прямых

17.

Неравенство треугольника

18.

Чему равна сумма углов в
равнобедренном
треугольнике?

19.

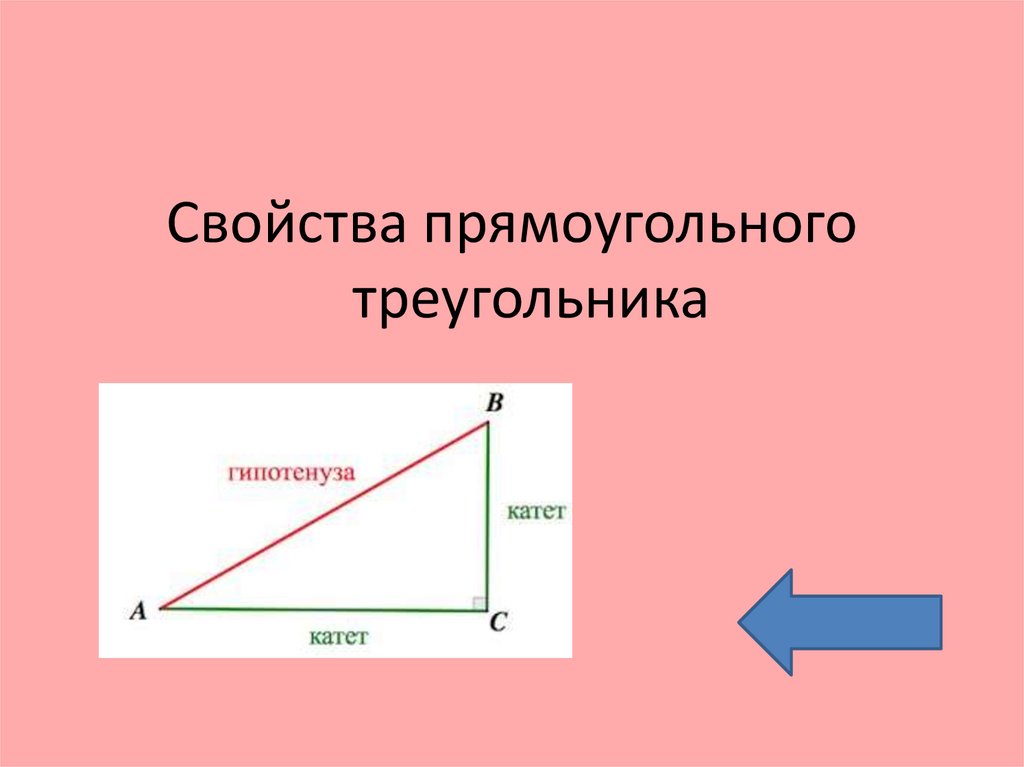
Свойства прямоугольного
треугольника