Similar presentations:
Магические квадраты
1.
Выполнила ученица 5 классаМОУ
«СОШ
п.
Орошаемый»Туктарова
Валерия
Учитель Укубасова А.Е.
2.
«В дни моей юности я в свободное времяразвлекался
тем,
что
составлял…
магические квадраты»
Бенджамин Франклин.
(17.1.1706 – 17.4.1790)
3.
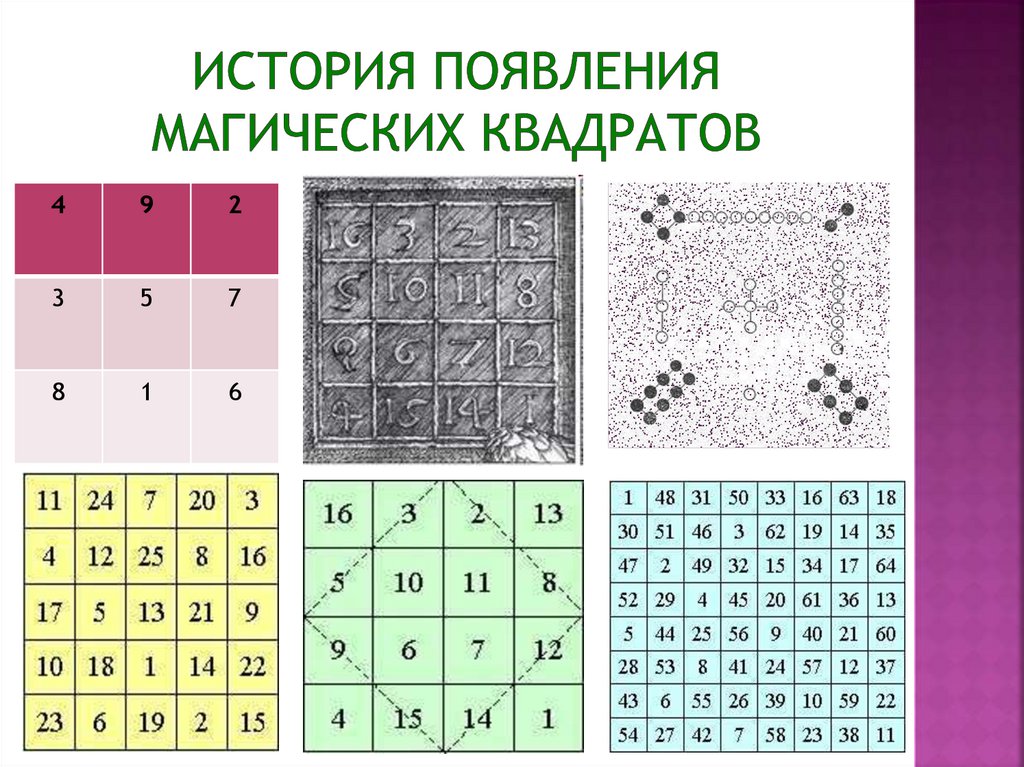
Задачи:познакомиться с историей появления и
названиями магических квадратов
изучить один из способов заполнения
магических квадратов 3 порядка
исследовать количество решений для
магических квадратов 3 порядка
4.
49
2
3
5
7
8
1
6
5.
6.
712
1
14
2
13
8
11
16
3
10
5
9
6
15
4
7.
Магический квадрат 4×4,изображённый на гравюре
Альбрехта Дюрера «Меланхолия»,
считается самым ранним в
европейском искусстве.
Два средних числа в нижнем ряду
указывают дату создания картины
(1514 г.).
8.
Эта сумма также встречается во всехугловых квадратах 2×2, в
центральном квадрате, в квадрате из
угловых клеток, в прямоугольниках,
образованных парами средних клеток
на противоположных сторонах.
Большинство дополнительных
симметрий связано с тем, что сумма
любых двух центрально симметрично
расположенных чисел равна 17.
9.
Латинским квадратом называется квадрат n*nклеток, в которых написаны числа от 1 до n, притом
так, что в каждой строке и каждом столбце
встречаются все эти числа по одному разу.
1
2
3
2
3
1
3
1
2
10.
Бенджамин Франклин составил квадрат 16×16, который помимоналичия постоянной суммы 2056 во всех строках, столбцах и
диагоналях имел еще одно дополнительное свойство. Если
вырезать из листа бумаги квадрат 4×4 и уложить этот лист на
большой квадрат так, чтобы 16 клеток большего квадрата попали в
эту прорезь, то сумма чисел, появившихся в этой прорези, куда
бы мы ее не положили, будет одна и та же – 2056.
200
217
232
249
8
25
40
57
72
89
104
121
136
153
168
185
58
39
26
7
250
231
218
199
186
167
154
135
122
103
90
71
198
219
230
251
6
27
38
59
70
91
102
123
134
155
166
187
60
37
28
5
252
229
220
197
188
165
156
133
124
101
92
69
201
216
233
248
9
24
41
56
73
88
105
120
137
152
169
184
55
42
23
10
247
234
215
202
183
170
151
138
119
106
87
74
203
214
235
246
11
22
43
54
75
86
107
118
139
150
171
182
53
44
21
12
245
236
213
204
181
172
149
140
117
108
85
76
205
212
237
244
13
20
45
52
77
84
109
116
141
148
173
180
51
46
19
14
243
238
211
206
179
174
147
142
115
110
83
78
207
210
239
242
15
18
47
50
79
82
111
114
143
146
175
178
49
48
17
16
241
240
209
208
177
176
145
144
113
112
81
80
196
221
228
253
4
29
36
61
68
93
100
125
132
157
164
189
62
35
30
3
254
227
222
195
190
163
158
131
126
99
94
67
194
223
226
255
2
31
34
63
66
95
98
127
130
159
162
191
64
33
32
1
256
225
224
193
192
161
160
129
128
97
96
65
11.
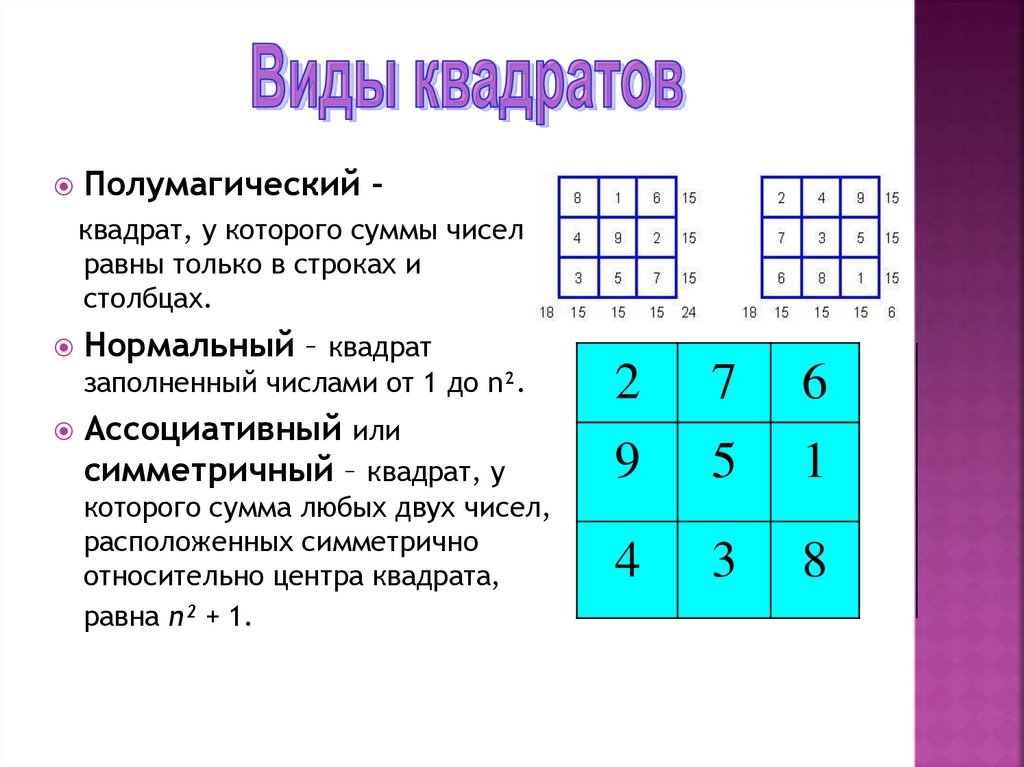
Полумагический –квадрат, у которого суммы чисел
равны только в строках и
столбцах.
Нормальный – квадрат
заполненный числами от 1 до n².
Ассоциативный или
симметричный – квадрат, у
которого сумма любых двух чисел,
расположенных симметрично
относительно центра квадрата,
равна n² + 1.
2
7
6
9
5
1
4
3
8
12.
Суммачисел в каждой строке, столбце и
на диагоналях, называется магической
константой (М).
Магическая константа нормального
волшебного квадрата зависит только от n и
определяется формулой
13.
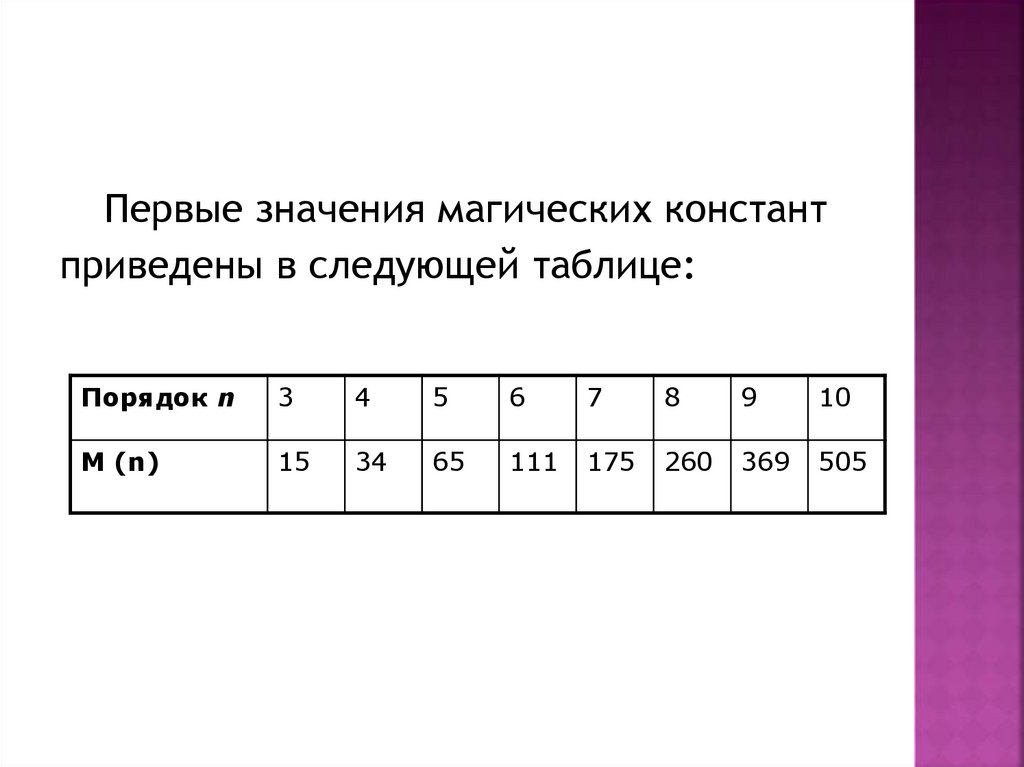
Первые значения магических константприведены в следующей таблице:
Порядок n
3
4
5
6
7
8
9
10
M (n)
15
34
65
111
175
260
369
505
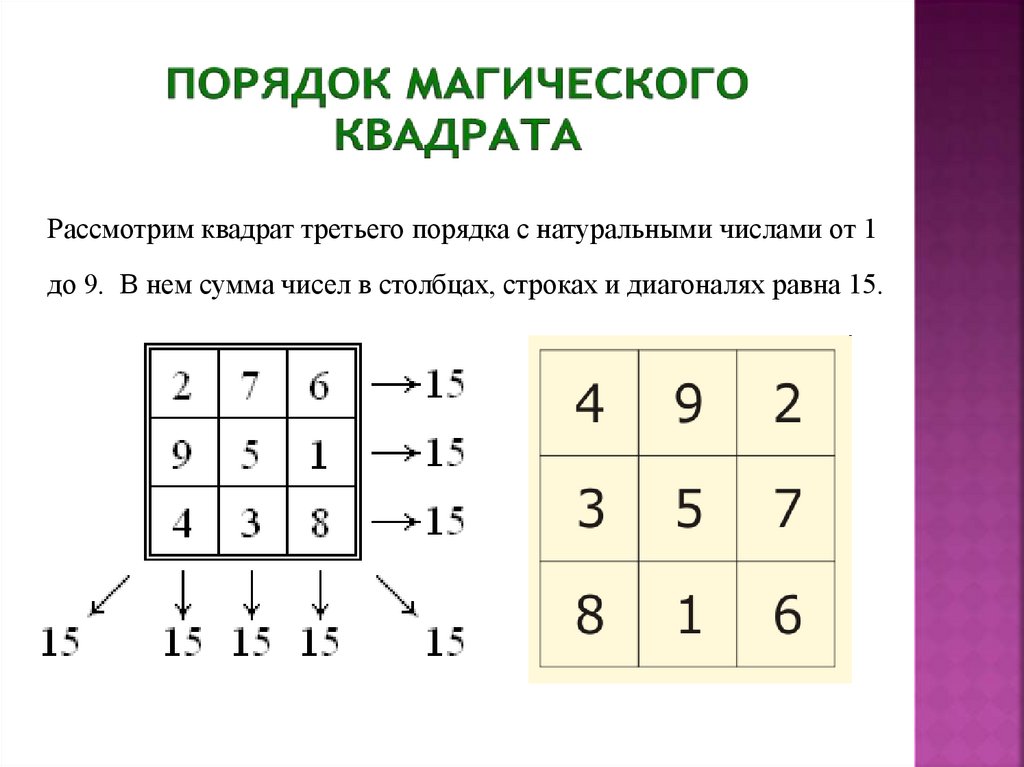
14.
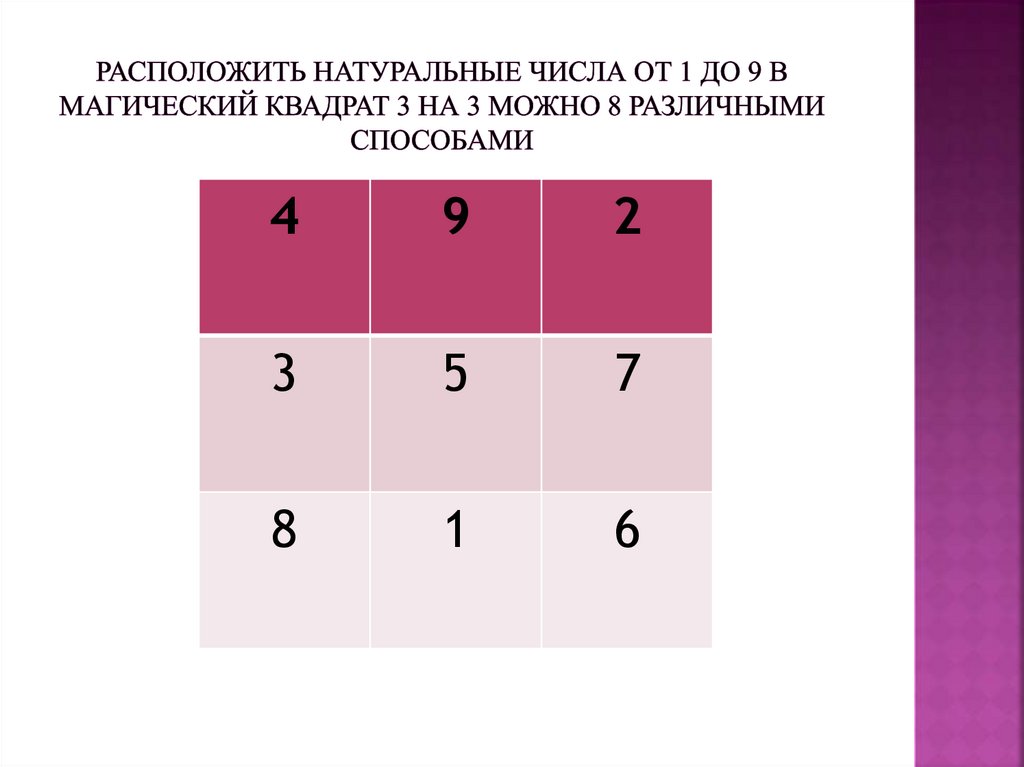
Рассмотрим квадрат третьего порядка с натуральными числами от 1до 9. В нем сумма чисел в столбцах, строках и диагоналях равна 15.
15.
49
2
3
5
7
8
1
6
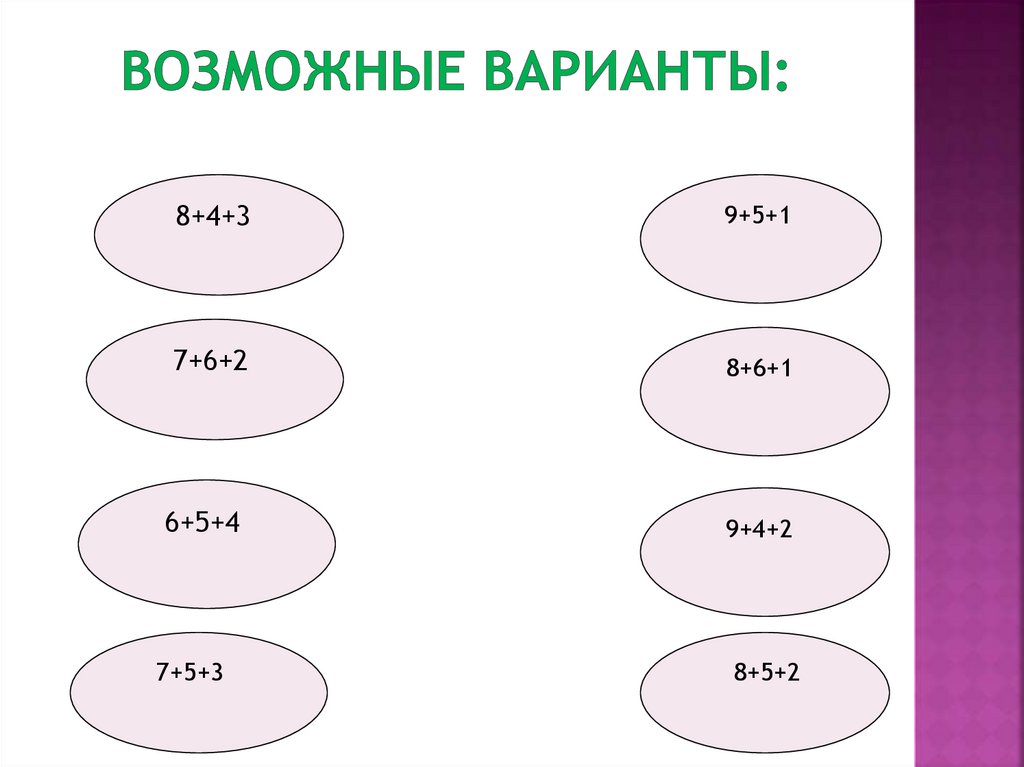
16.
8+4+39+5+1
7+6+2
8+6+1
6+5+4
7+5+3
9+4+2
8+5+2
17.
Квадрат разделен на 9 равных клеток. Расставьте в этихклетках числа 1, 2, 3, 4, 5, 6, 7, 8, 9 так, чтобы сумма
чисел в каждой строке и в каждом столбике равнялась
15.
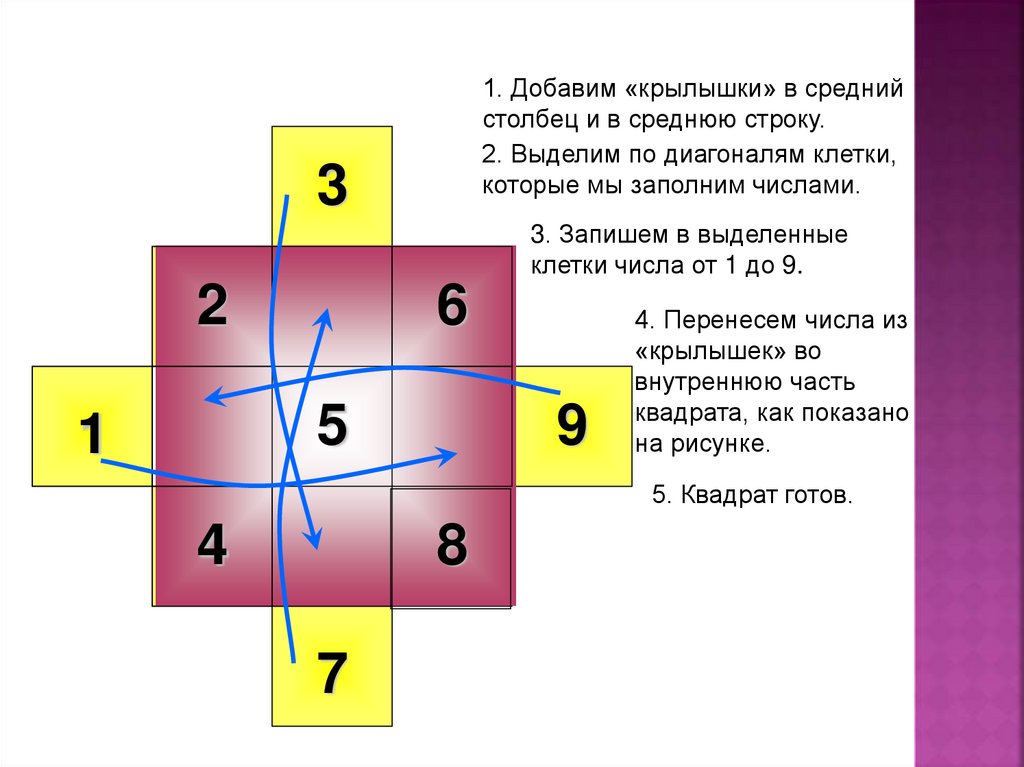
18.
1. Добавим «крылышки» в среднийстолбец и в среднюю строку.
2. Выделим по диагоналям клетки,
которые мы заполним числами.
3
3. Запишем в выделенные
клетки числа от 1 до 9.
2
6
5
1
9
4. Перенесем числа из
«крылышек» во
внутреннюю часть
квадрата, как показано
на рисунке.
5. Квадрат готов.
4
8
7
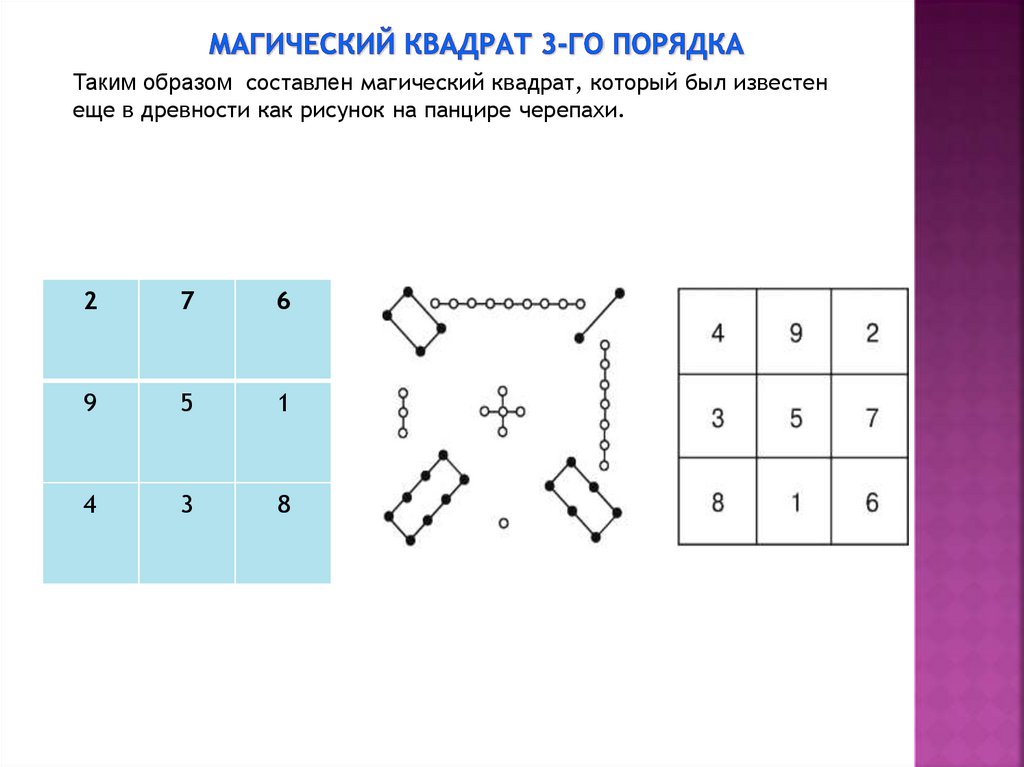
19.
Таким образом составлен магический квадрат, который был известенеще в древности как рисунок на панцире черепахи.
2
7
6
9
5
1
4
3
8
20.
Магический квадрат2
В клетках квадрата переставьте числа так, чтобы по любой вертикали,
горизонтали и диагонали их суммы были равны между собой:
3
5
7
9
11
13
15 17 19
Заполним квадрат числами
3, 5, 7, 9, 11, 13, 15, 17 и 19
по алгоритму.
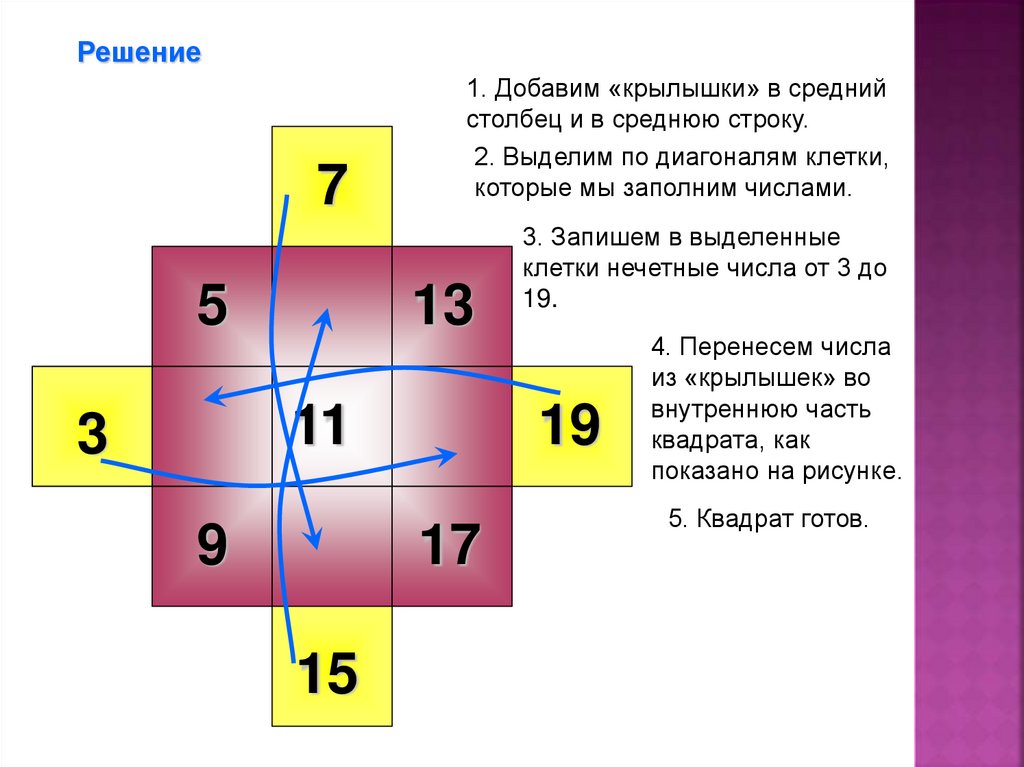
21.
Решение7
5
1. Добавим «крылышки» в средний
столбец и в среднюю строку.
2. Выделим по диагоналям клетки,
которые мы заполним числами.
13
11
3
9
19
17
15
3. Запишем в выделенные
клетки нечетные числа от 3 до
19.
4. Перенесем числа
из «крылышек» во
внутреннюю часть
квадрата, как
показано на рисунке.
5. Квадрат готов.
22.
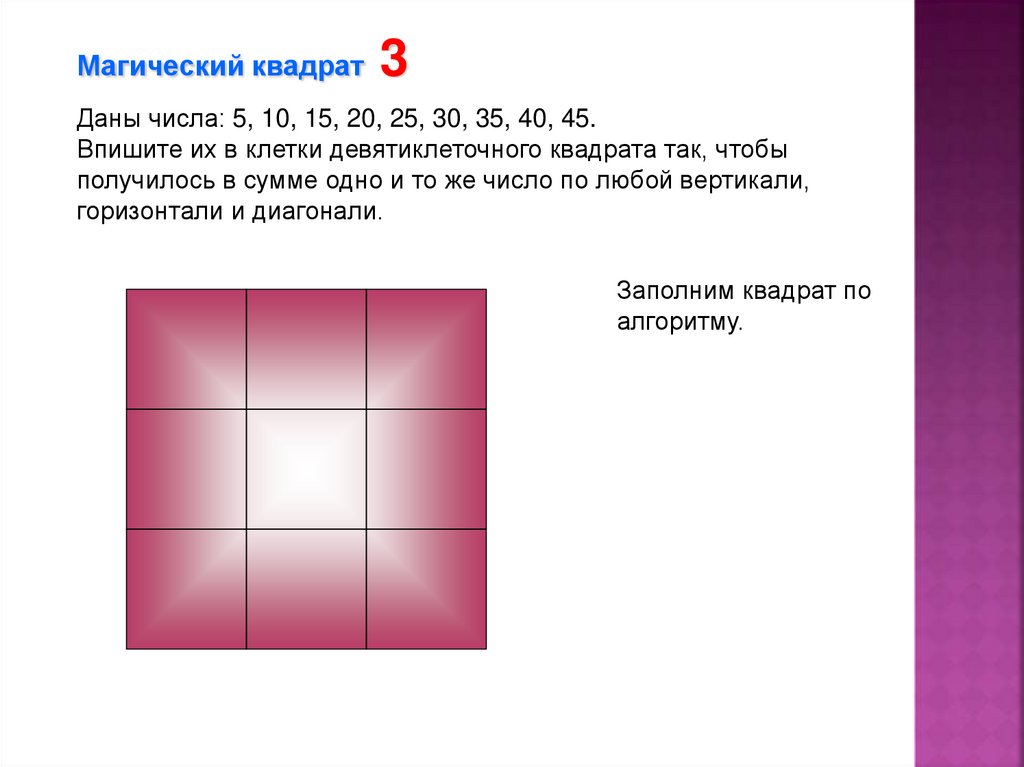
Магический квадрат3
Даны числа: 5, 10, 15, 20, 25, 30, 35, 40, 45.
Впишите их в клетки девятиклеточного квадрата так, чтобы
получилось в сумме одно и то же число по любой вертикали,
горизонтали и диагонали.
Заполним квадрат по
алгоритму.
23.
Решение1. Добавим «крылышки» в средний
столбец и в среднюю строку.
2. Выделим по диагоналям клетки,
которые мы заполним числами.
3. Запишем в выделенные
клетки заданные числа.
15
10
30
25
5
45
4. Перенесем числа
из «крылышек» во
внутреннюю часть
квадрата, как
показано на рисунке.
5. Квадрат готов.
20
40
35
24.
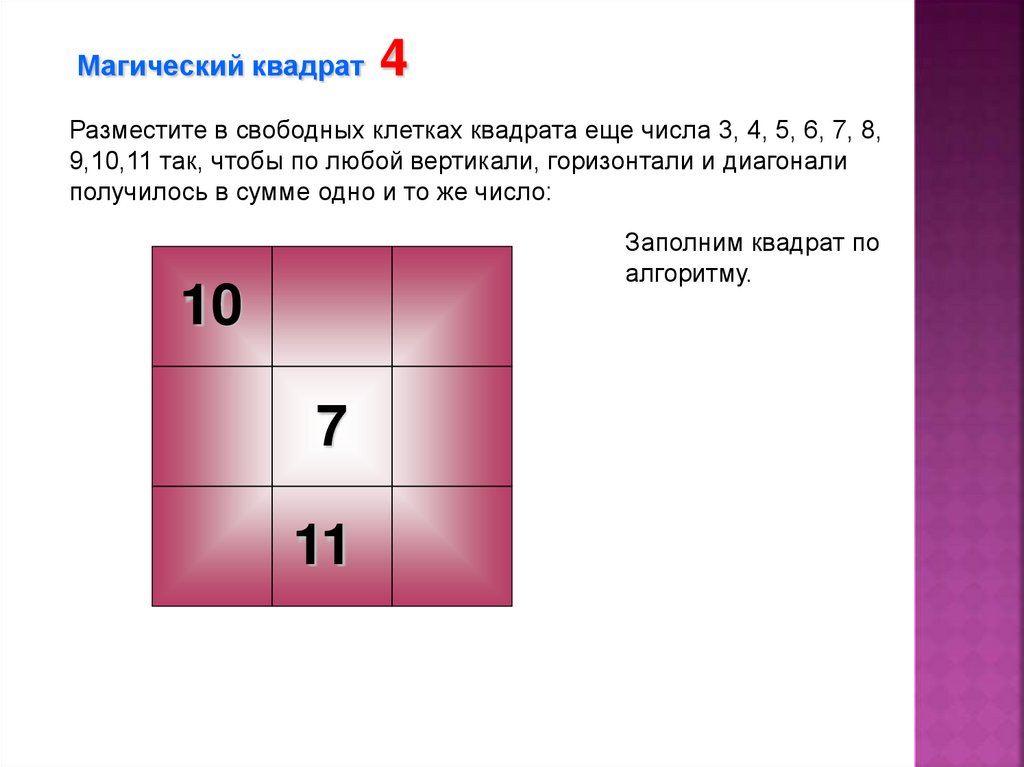
Магический квадрат4
Разместите в свободных клетках квадрата еще числа 3, 4, 5, 6, 7, 8,
9,10,11 так, чтобы по любой вертикали, горизонтали и диагонали
получилось в сумме одно и то же число:
Заполним квадрат по
алгоритму.
10
7
11
25.
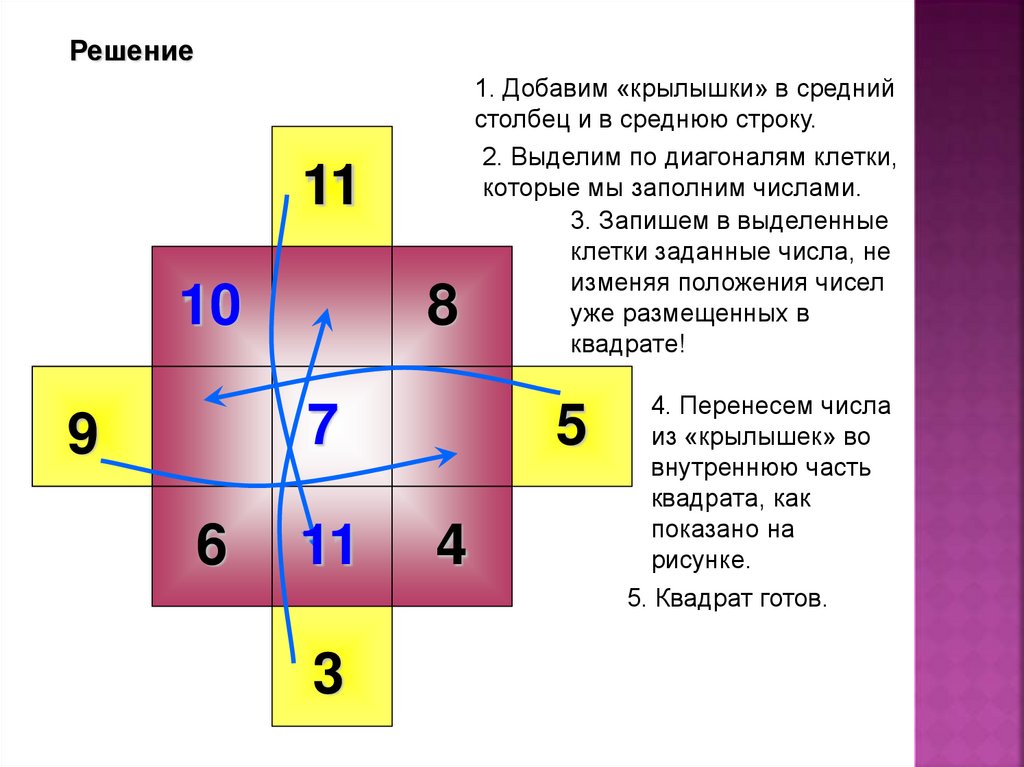
Решение11
10
8
7
9
6
11
3
1. Добавим «крылышки» в средний
столбец и в среднюю строку.
2. Выделим по диагоналям клетки,
которые мы заполним числами.
3. Запишем в выделенные
клетки заданные числа, не
изменяя положения чисел
уже размещенных в
квадрате!
5
4
4. Перенесем числа
из «крылышек» во
внутреннюю часть
квадрата, как
показано на
рисунке.
5. Квадрат готов.
26.
Магических квадрат 4 порядка существует 8804
5
14
11
1
15
8
10
16
2
9
7
13
12
3
6
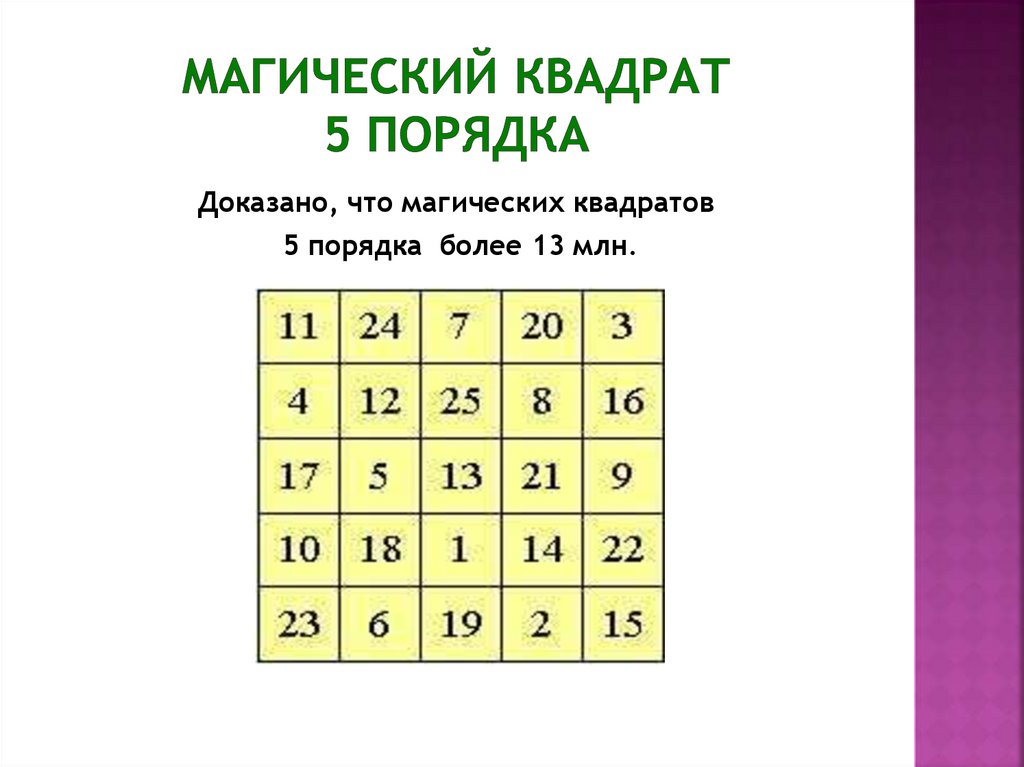
27.
Доказано, что магических квадратов5 порядка более 13 млн.
28.
Этот квадрат 8 порядка составлен в 18 в.великим Леонардом Эйлером. Каждый ряд в этом
квадрате даёт сумму 260, а половина ряда –130.
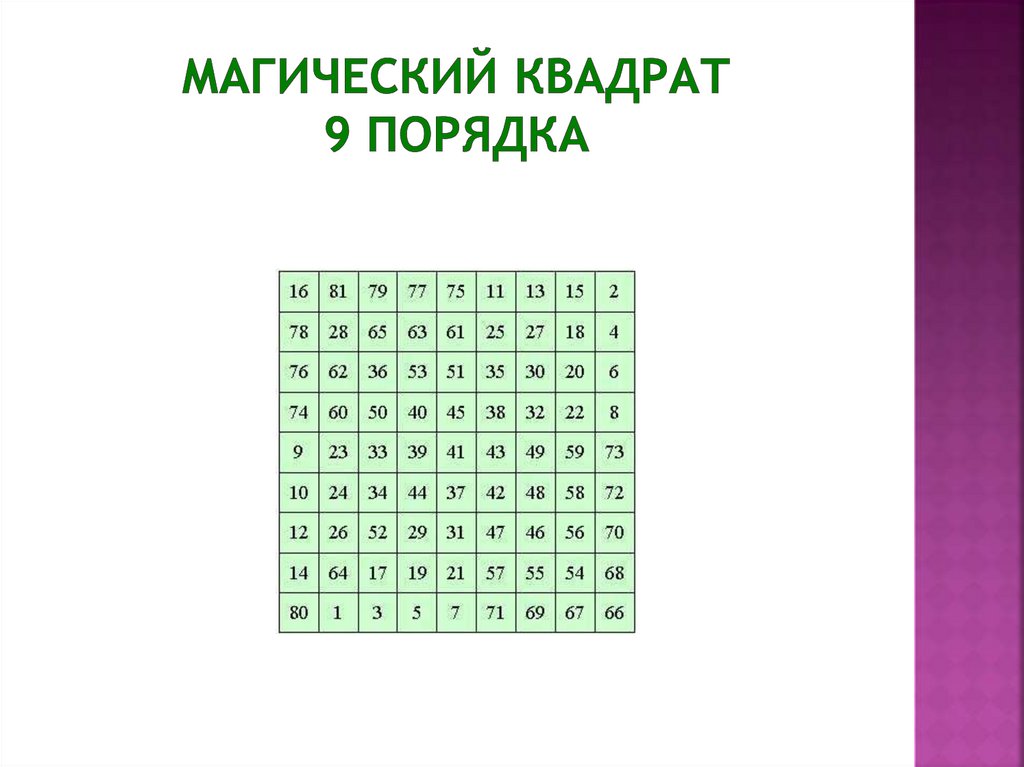
29.
30.
Выводы1. Магический квадрат – квадрат
древнекитайского происхождения.
2. Универсального способа заполнения
магических квадратов нет.
3. Квадрат 3 порядка можно получить
достраиванием до ступенчатой ромбовидной
фигуры.

















 mathematics
mathematics








