Similar presentations:
Магический квадрат
1.
«Магический квадрат»2.
Цель: изучить магические квадраты.Задачи:
1. Изучить историю возникновения магических квадратов,.
2. Ознакомиться с видами и основными методами
построения магических квадратов; применением
магических квадратов в жизни.
3. Научиться строить магические квадраты любого
порядка.
4. Составить психологический портрет личности по
квадрату Пифагора.
3.
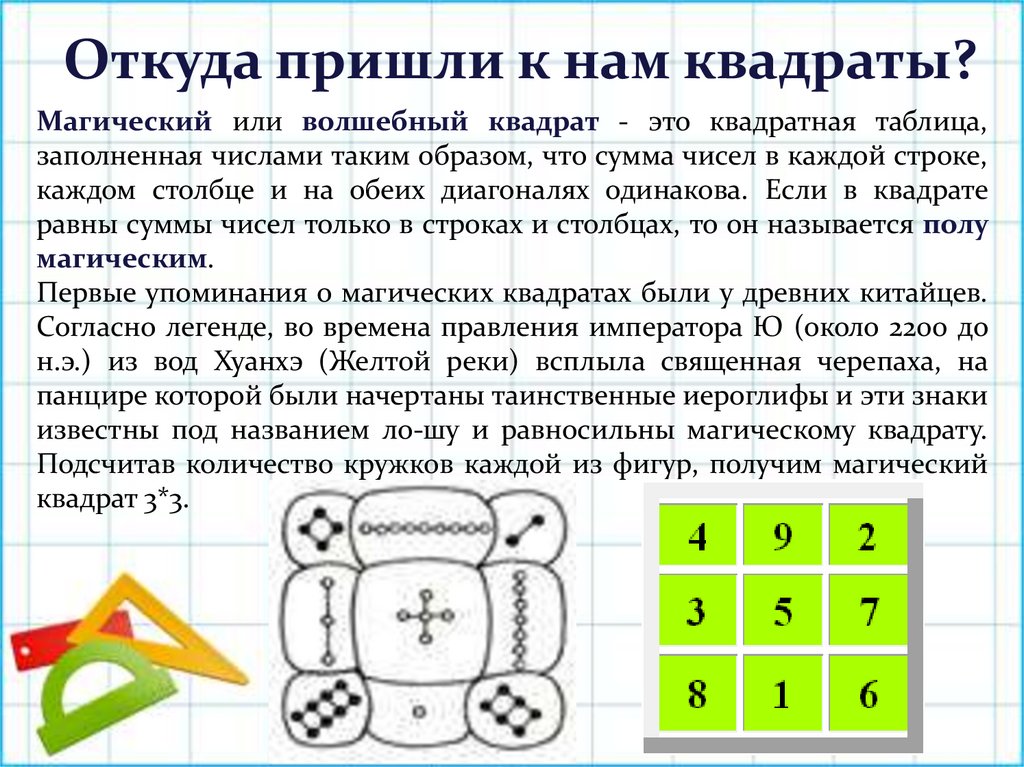
Откуда пришли к нам квадраты?Магический или волшебный квадрат - это квадратная таблица,
заполненная числами таким образом, что сумма чисел в каждой строке,
каждом столбце и на обеих диагоналях одинакова. Если в квадрате
равны суммы чисел только в строках и столбцах, то он называется полу
магическим.
Первые упоминания о магических квадратах были у древних китайцев.
Согласно легенде, во времена правления императора Ю (около 2200 до
н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на
панцире которой были начертаны таинственные иероглифы и эти знаки
известны под названием ло-шу и равносильны магическому квадрату.
Подсчитав количество кружков каждой из фигур, получим магический
квадрат 3*3.
4.
Откуда пришли к нам квадраты?Самый ранний уникальный магический квадрат обнаружен в надписи
XI века в Индийском городе Кхаджурахо:
Это первый магический квадрат, относящийся к
разновидности так называемых «дьявольских»
квадратов.
Из Китая магические квадраты распространились
сначала в Индию, а затем и в другие страны. В
начале XVI века знаменитый немецкий художник
Альбрехт Дюрер увековечил магический квадрат в искусстве,
изобразив его на гравюре «Меланхолия». Дата создания гравюры (1514
год) указана числами, стоящими в двух центральных клетках нижней
строки.
5.
Откуда пришли к нам квадраты?В IX веке. интерес к магическим квадратам вспыхнул с новой силой. Их
стали исследовать с помощью методов высшей алгебры. Получение
магических квадратов считалось популярным развлечением среди
математиков. Ими создавались огромные квадраты, например, 45*45,
содержащие числа от 1 до 2025. Были придуманы способы построения
магических квадратов любого размера, однако до сих пор не найдена
формула, по которой можно было бы найти количество магических
квадратов данного размера.
В наше время магические квадраты продолжают привлекать к себе
внимание не только специалистов, но и любителей математических игр
и развлечений. За последнее столетие значительно возросло число книг
по занимательной математике, в которых содержатся головоломки и
задачки, связанные с необычными квадратами.
6.
Виды магическихквадратов и способы
их заполнения
7.
Магический квадрат Ян Хуэя (Китай)Математик Ян Хуэй в XIII веке рассматривал магические квадраты не
только третьего, но и больших порядков. Некоторые из его квадратов
были достаточно сложны, однако он всегда давал правила для их
построения. Он сумел построить магический квадрат шестого порядка,
причем последний оказался почти ассоциативным (в нем только две
пары центрально противолежащих чисел не дают сумму 37):
8.
Квадрат Альбрехта ДюрераСумма чисел на любой горизонтали, вертикали и диагонали равна 34.
Эта сумма также встречается во всех угловых квадратах 2*2, в
центральном квадрате (10+11+6+7), в квадрате из угловых клеток
(16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и
3+5+12+14), в прямоугольниках, образованных парами средних клеток на
противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство
дополнительных симметрий связано с тем, что сумма любых двух
центрально симметрично расположенных чисел равна 17.
9.
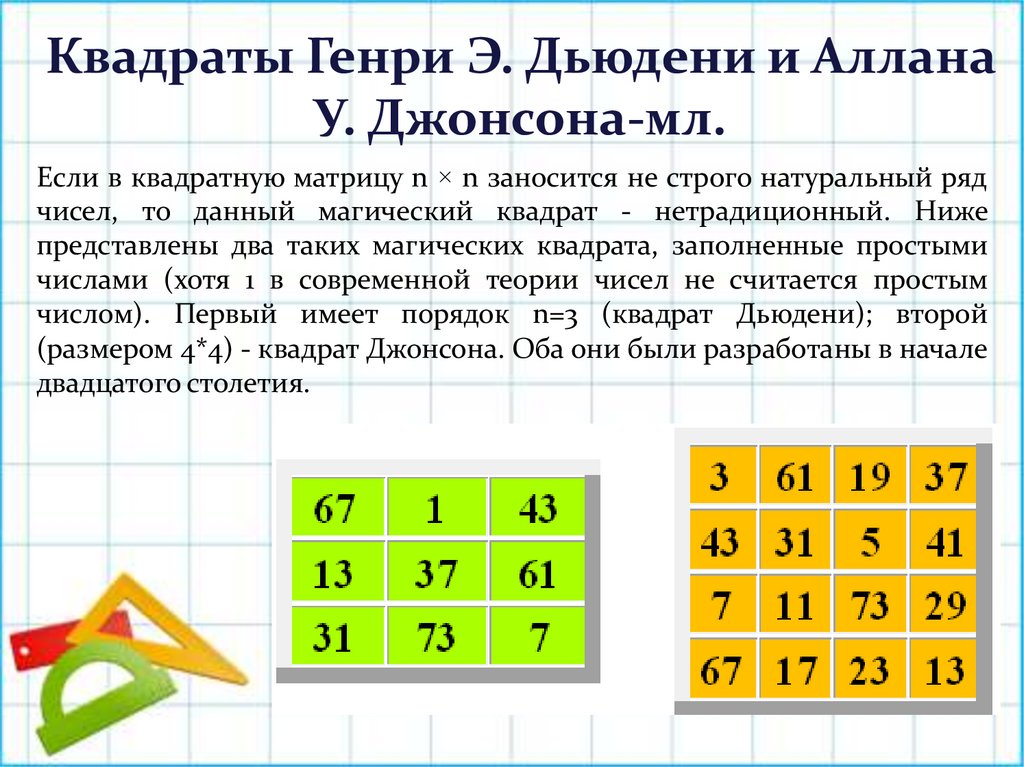
Квадраты Генри Э. Дьюдени и АлланаУ. Джонсона-мл.
Если в квадратную матрицу n × n заносится не строго натуральный ряд
чисел, то данный магический квадрат - нетрадиционный. Ниже
представлены два таких магических квадрата, заполненные простыми
числами (хотя 1 в современной теории чисел не считается простым
числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй
(размером 4*4) - квадрат Джонсона. Оба они были разработаны в начале
двадцатого столетия.
10.
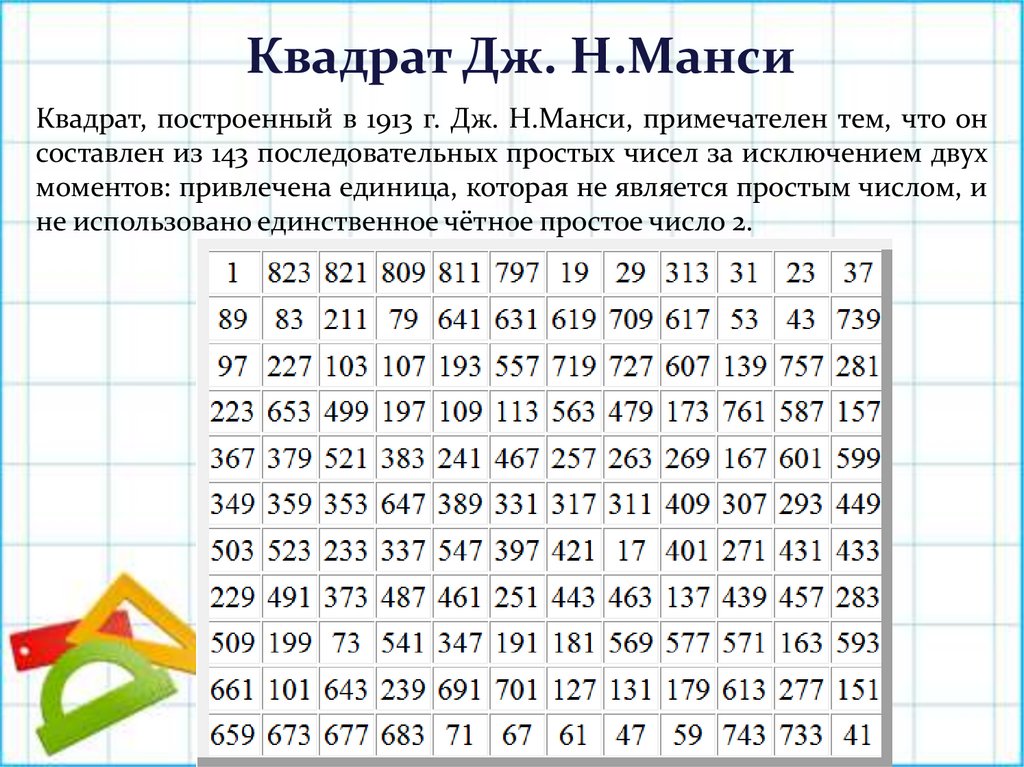
Квадрат Дж. Н.МансиКвадрат, построенный в 1913 г. Дж. Н.Манси, примечателен тем, что он
составлен из 143 последовательных простых чисел за исключением двух
моментов: привлечена единица, которая не является простым числом, и
не использовано единственное чётное простое число 2.
11.
Метод Клод Баше де МезириакаПусть n – нечётное число, нужно построить квадрат nхn с числами от 1
до n2.
1. Все числа от 1 до n2 записываем в клеточки по диагонали (по n чисел в
ряд), чтобы образовался диагональный квадрат.
2. Выделяем в его центре квадрат n*n. Это и есть основа (ещё не все
клетки заполнены) будущего магического квадрата.
12.
Метод Клод Баше де МезириакаКаждый находящийся вне центрального квадрата числовой «уголок»
аккуратно переносим внутрь – к противоположной стороне квадрата.
Числа этих «уголков» должны заполнить все пустые клетки.
13.
Метод Клод Баше де МезириакаМагический квадрат построен. Теперь можно проверить, что в таком
магическом квадрате n*n из первых n2 натуральных чисел сумма чисел
по каждой линии (строка, столбец, диагональ) в точности равна
Вывод: магических квадратов 2*2 не существует. Квадрат размером 2*2
должен был бы состоять из чисел 1,2,3,4, а его постоянная была бы равна 5.
У такого квадрата по две строки, столбца и диагонали. Чтобы квадрат стал
магическим, надо представить число 5 в виде суммы двух данных чисел
шестью различными способами, но это сделать не возможно! Ведь таких
комбинаций всего две: 1+4 и 2+3. Как ни расставляй числа в клетках
таблицы, их сумма будет равна 5 либо в каждой строке, либо в обоих
столбцах, либо по диагоналям, но никак не одновременно.
Существует единственный магический квадрат 3*3, так
как остальные магические квадраты 3*3 получаются из
него либо перестановкой строк или столбцов, либо
путем поворота исходного квадрата на 900 или на 1800.
14.
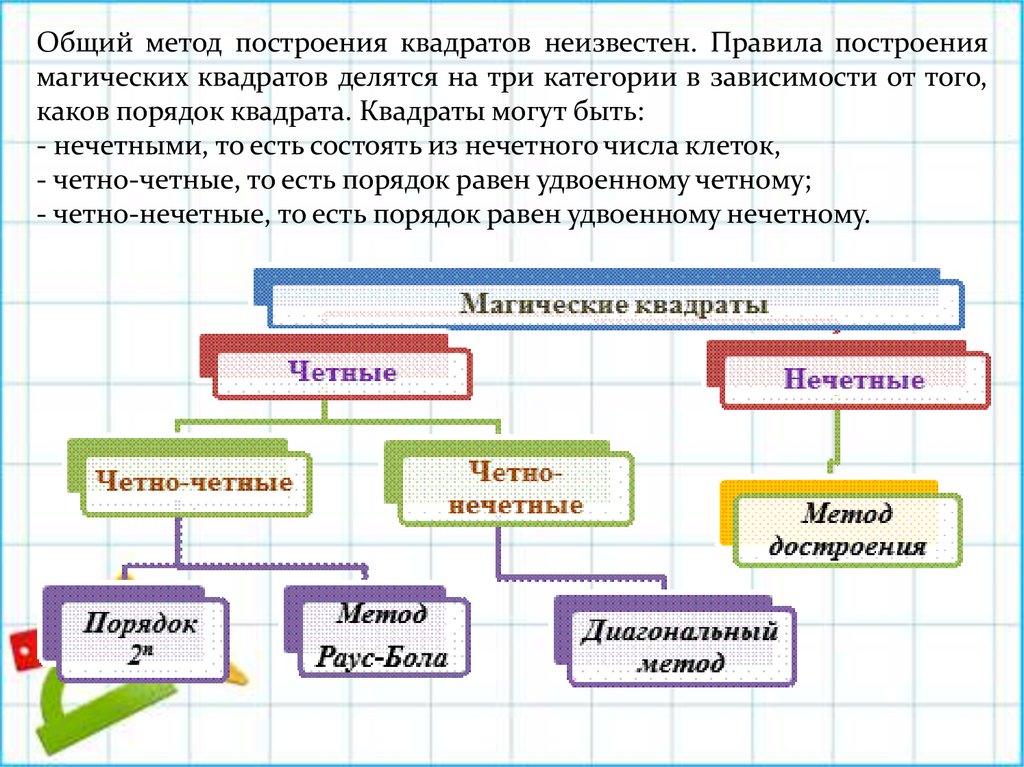
Общий метод построения квадратов неизвестен. Правила построениямагических квадратов делятся на три категории в зависимости от того,
каков порядок квадрата. Квадраты могут быть:
- нечетными, то есть состоять из нечетного числа клеток,
- четно-четные, то есть порядок равен удвоенному четному;
- четно-нечетные, то есть порядок равен удвоенному нечетному.
15.
Магические квадратынечётного порядка
16.
Метод достроения1) Построим квадрат с 25 клетками и временно достроим его до
симметричной ступенчатой ромбовидной фигуры. Достроенные клеточки
обозначим символом *.
2) В полученной фигуре располагаем по порядку
косыми рядами сверху-вниз-направо 25 целых
чисел от 1 до 25.
17.
3). Каждое число, расположенное вне исходного (выделенного) квадрата,следует перенести вдоль того же ряда или столбца ровно на столько клеток от
той клетки, которую оно занимает, каков порядок квадрата – на пять.
4) Таким образом, все ячейки квадрата заполнены. Сумма чисел в столбцах,
строках и диагоналях равна 65.
18.
Магические квадратычётно-чётного
порядка
19.
Порядокn
2
Этот метод удобно рассматривать на примере магического квадрата 8*8.
1) Исходный квадрат разделим на соответствующее число квадратов
порядка 4. В данном случае таких квадратов будет 4. В каждом
подквадрате отметим диагональные элементы символом. Остальные
элементы построчно заполним порядковыми целыми числами в
направлении слева-направо и сверху-вниз. Числа, приходящиеся на
выделенные диагональные элементы, должны быть пропущены.
*
9
17
*
*
41
49
*
2
*
*
26
34
*
*
58
3
*
*
27
35
*
*
59
*
12
20
*
*
44
52
*
*
13
21
*
*
45
53
*
6
*
*
30
38
*
*
62
7
*
*
31
39
*
*
63
*
16
24
*
*
48
56
*
20.
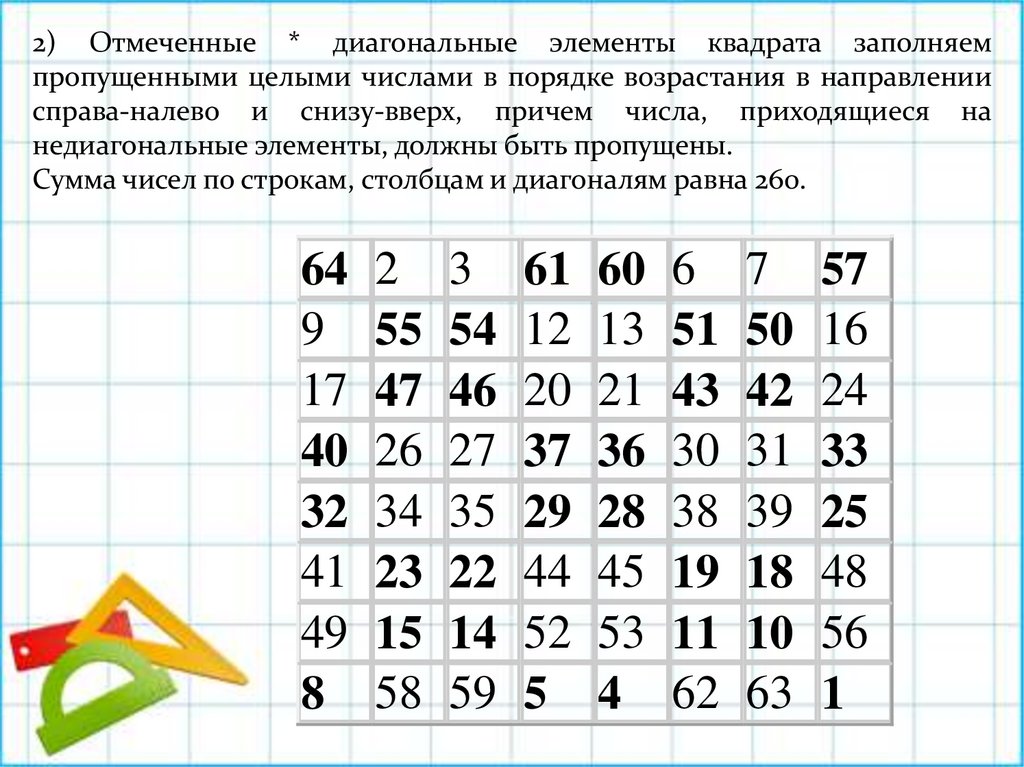
2) Отмеченные * диагональные элементы квадрата заполняемпропущенными целыми числами в порядке возрастания в направлении
справа-налево и снизу-вверх, причем числа, приходящиеся на
недиагональные элементы, должны быть пропущены.
Сумма чисел по строкам, столбцам и диагоналям равна 260.
64
9
17
40
32
41
49
8
2
55
47
26
34
23
15
58
3
54
46
27
35
22
14
59
61
12
20
37
29
44
52
5
60
13
21
36
28
45
53
4
6
51
43
30
38
19
11
62
7
50
42
31
39
18
10
63
57
16
24
33
25
48
56
1
21.
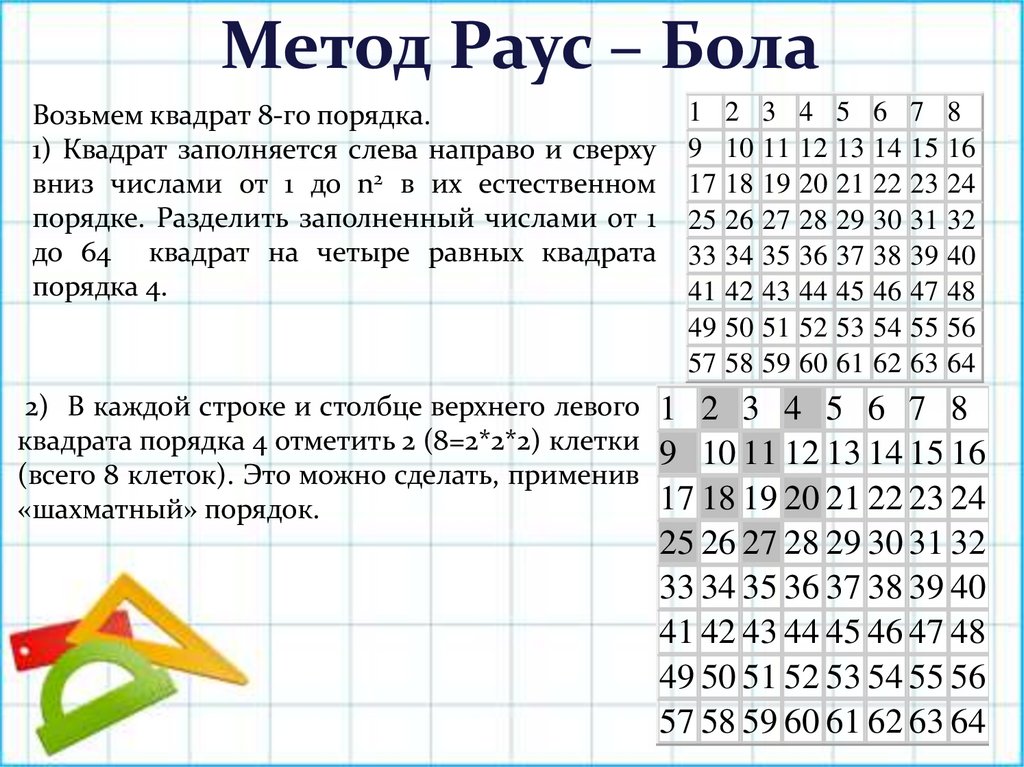
Метод Раус – БолаВозьмем квадрат 8-го порядка.
1) Квадрат заполняется слева направо и сверху
вниз числами от 1 до n2 в их естественном
порядке. Разделить заполненный числами от 1
до 64 квадрат на четыре равных квадрата
порядка 4.
2) В каждой строке и столбце верхнего левого
квадрата порядка 4 отметить 2 (8=2*2*2) клетки
(всего 8 клеток). Это можно сделать, применив
«шахматный» порядок.
1
9
17
25
33
41
49
57
2
10
18
26
34
42
50
58
3
11
19
27
35
43
51
59
4
12
20
28
36
44
52
60
5
13
21
29
37
45
53
61
6
14
22
30
38
46
54
62
7
15
23
31
39
47
55
63
8
16
24
32
40
48
56
64
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
22.
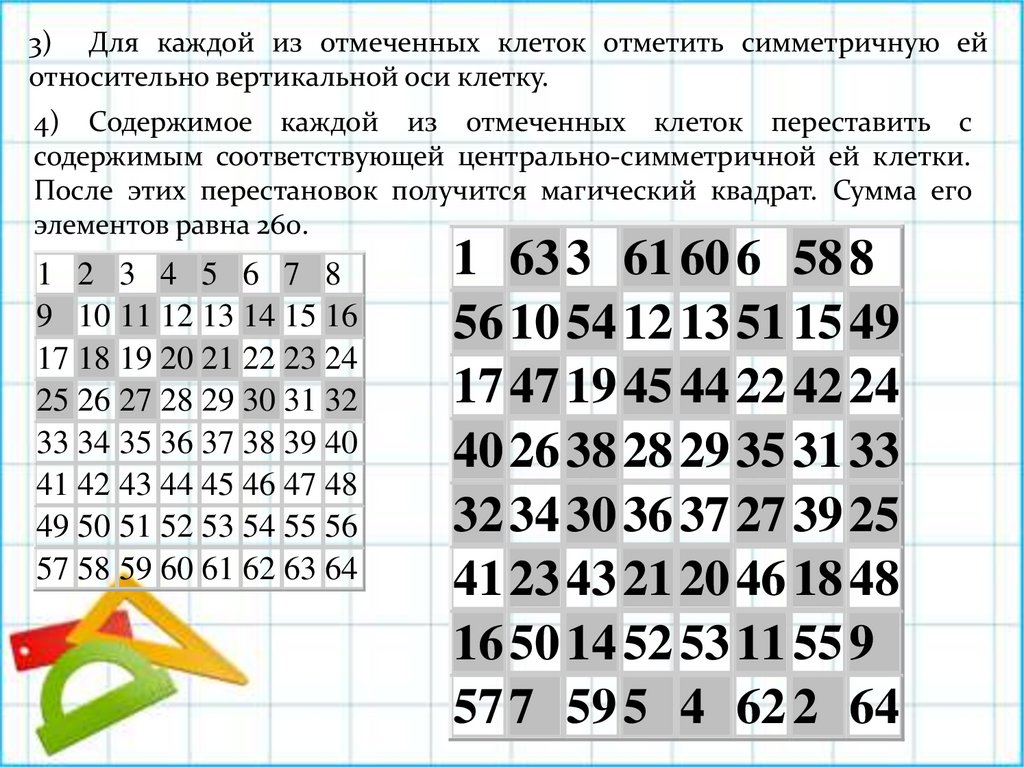
3) Для каждой из отмеченных клеток отметить симметричную ейотносительно вертикальной оси клетку.
4) Содержимое каждой из отмеченных клеток переставить с
содержимым соответствующей центрально-симметричной ей клетки.
После этих перестановок получится магический квадрат. Сумма его
элементов равна 260.
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
1 63 3 61 60 6 58 8
56 10 54 12 13 51 15 49
17 47 19 45 44 22 42 24
40 26 38 28 29 35 31 33
32 34 30 36 37 27 39 25
41 23 43 21 20 46 18 48
16 50 14 52 53 11 55 9
57 7 59 5 4 62 2 64
23.
Магические квадратычётно-нечётного
порядка
24.
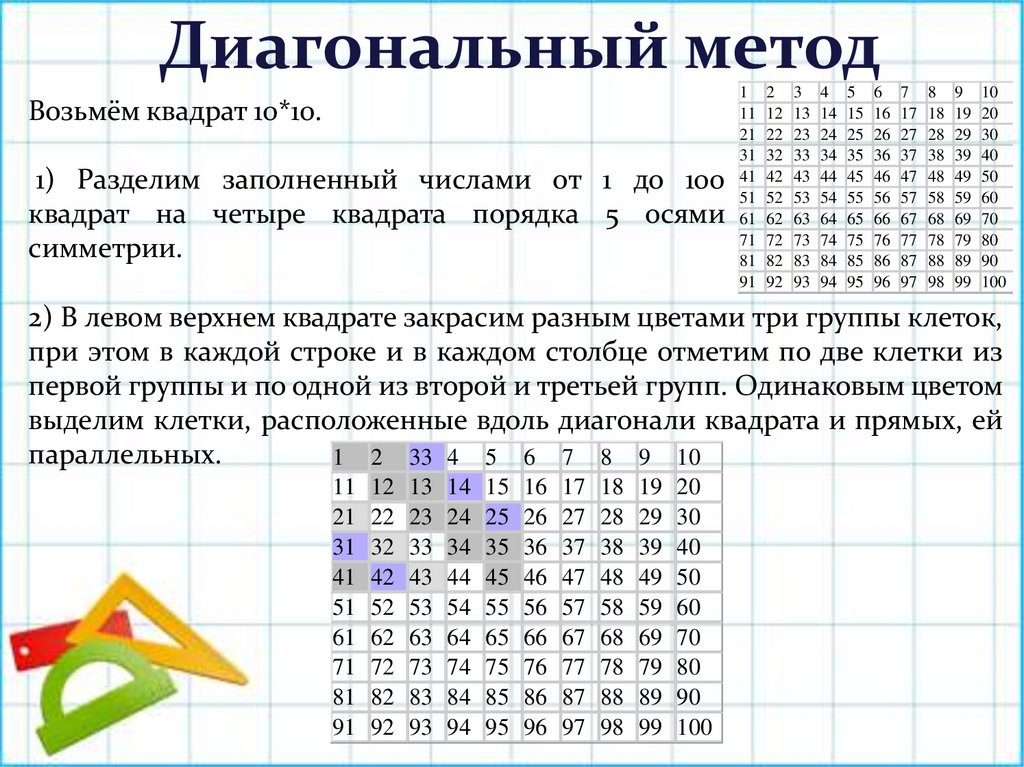
Диагональный методВозьмём квадрат 10*10.
1) Разделим заполненный числами от 1 до 100
квадрат на четыре квадрата порядка 5 осями
симметрии.
1
11
21
31
41
51
61
71
81
91
2
12
22
32
42
52
62
72
82
92
3
13
23
33
43
53
63
73
83
93
4
14
24
34
44
54
64
74
84
94
5
15
25
35
45
55
65
75
85
95
6
16
26
36
46
56
66
76
86
96
7
17
27
37
47
57
67
77
87
97
8
18
28
38
48
58
68
78
88
98
9
19
29
39
49
59
69
79
89
99
10
20
30
40
50
60
70
80
90
100
2) В левом верхнем квадрате закрасим разным цветами три группы клеток,
при этом в каждой строке и в каждом столбце отметим по две клетки из
первой группы и по одной из второй и третьей групп. Одинаковым цветом
выделим клетки, расположенные вдоль диагонали квадрата и прямых, ей
параллельных.
1 2 33 4 5 6 7 8 9 10
11
21
31
41
51
61
71
81
91
12
22
32
42
52
62
72
82
92
13
23
33
43
53
63
73
83
93
14
24
34
44
54
64
74
84
94
15
25
35
45
55
65
75
85
95
16
26
36
46
56
66
76
86
96
17
27
37
47
57
67
77
87
97
18
28
38
48
58
68
78
88
98
19
29
39
49
59
69
79
89
99
20
30
40
50
60
70
80
90
100
25.
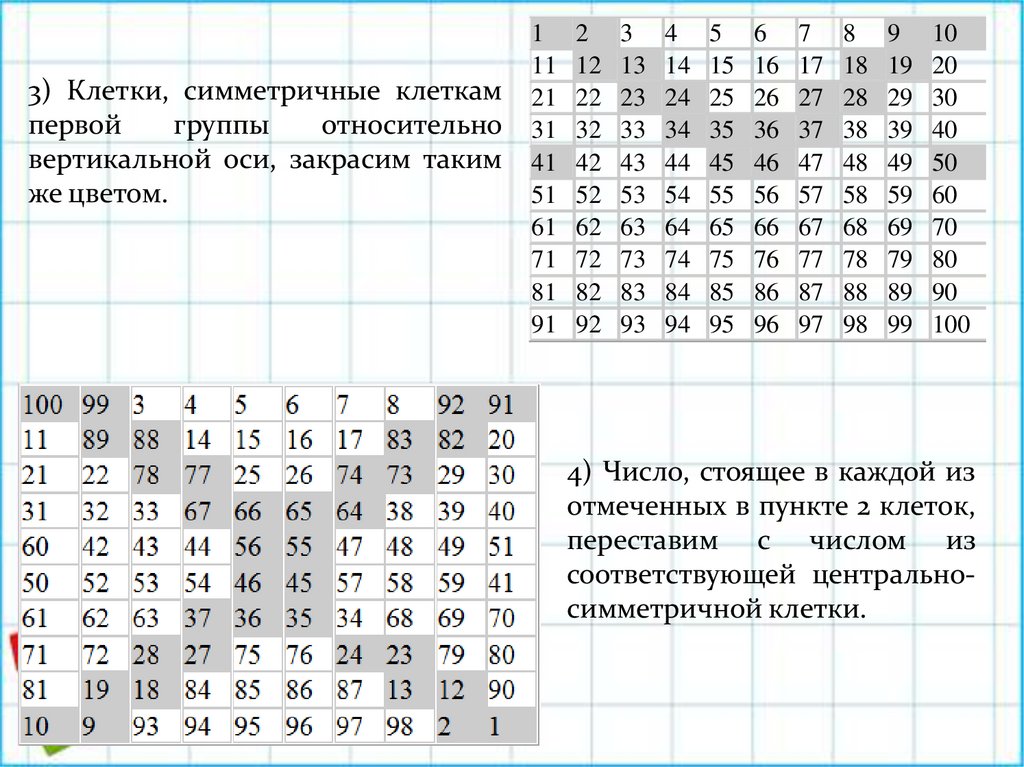
3) Клетки, симметричные клеткампервой
группы
относительно
вертикальной оси, закрасим таким
же цветом.
1
11
21
31
41
51
61
71
81
91
2
12
22
32
42
52
62
72
82
92
3
13
23
33
43
53
63
73
83
93
4
14
24
34
44
54
64
74
84
94
5
15
25
35
45
55
65
75
85
95
6
16
26
36
46
56
66
76
86
96
7
17
27
37
47
57
67
77
87
97
8
18
28
38
48
58
68
78
88
98
9
19
29
39
49
59
69
79
89
99
10
20
30
40
50
60
70
80
90
100
4) Число, стоящее в каждой из
отмеченных в пункте 2 клеток,
переставим с числом из
соответствующей центральносимметричной клетки.
26.
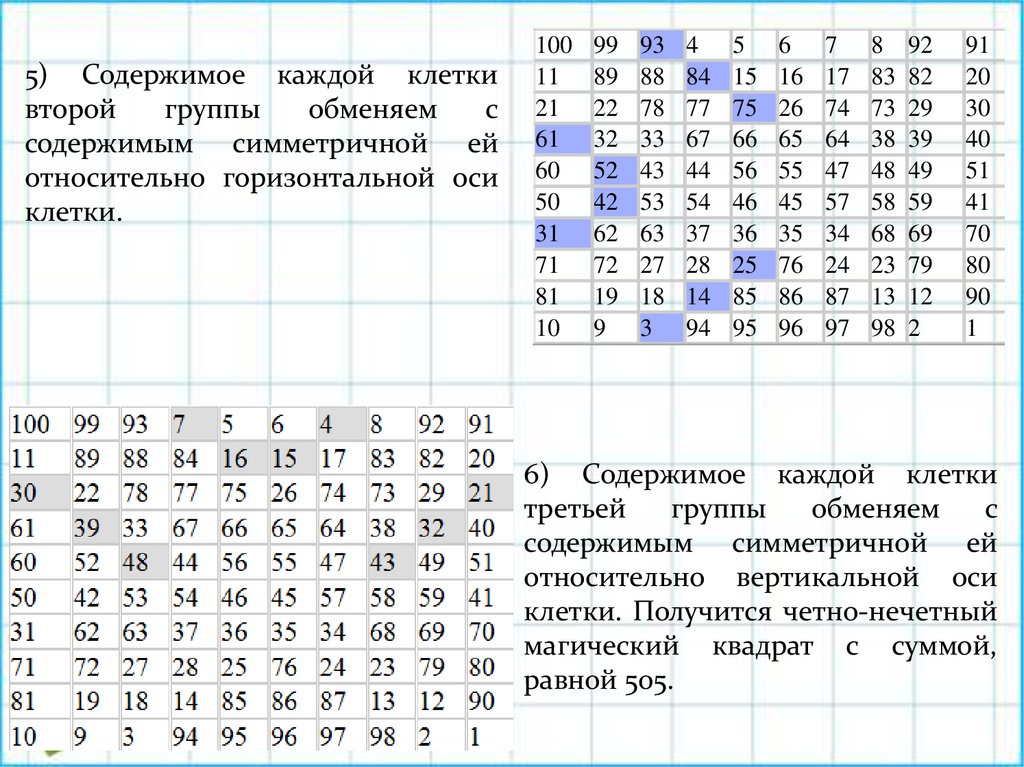
5) Содержимое каждой клеткивторой
группы
обменяем
с
содержимым симметричной ей
относительно горизонтальной оси
клетки.
100
11
21
61
60
50
31
71
81
10
99
89
22
32
52
42
62
72
19
9
93
88
78
33
43
53
63
27
18
3
4
84
77
67
44
54
37
28
14
94
5
15
75
66
56
46
36
25
85
95
6
16
26
65
55
45
35
76
86
96
7
17
74
64
47
57
34
24
87
97
8
83
73
38
48
58
68
23
13
98
92
82
29
39
49
59
69
79
12
2
91
20
30
40
51
41
70
80
90
1
6) Содержимое каждой клетки
третьей
группы
обменяем
с
содержимым симметричной ей
относительно вертикальной оси
клетки. Получится четно-нечетный
магический квадрат с суммой,
равной 505.
27.
Применениемагических квадратов
28.
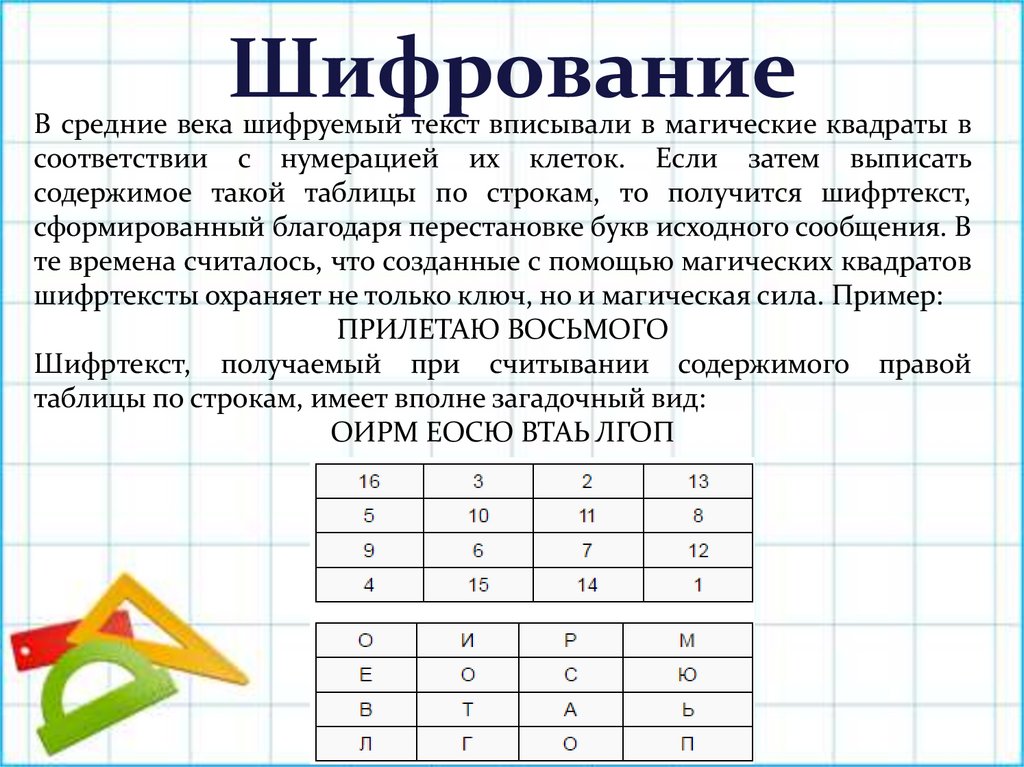
ШифрованиеВ средние века шифруемый текст вписывали в магические квадраты в
соответствии с нумерацией их клеток. Если затем выписать
содержимое такой таблицы по строкам, то получится шифртекст,
сформированный благодаря перестановке букв исходного сообщения. В
те времена считалось, что созданные с помощью магических квадратов
шифртексты охраняет не только ключ, но и магическая сила. Пример:
ПРИЛЕТАЮ ВОСЬМОГО
Шифртекст, получаемый при считывании содержимого правой
таблицы по строкам, имеет вполне загадочный вид:
ОИРМ ЕОСЮ ВТАЬ ЛГОП
29.
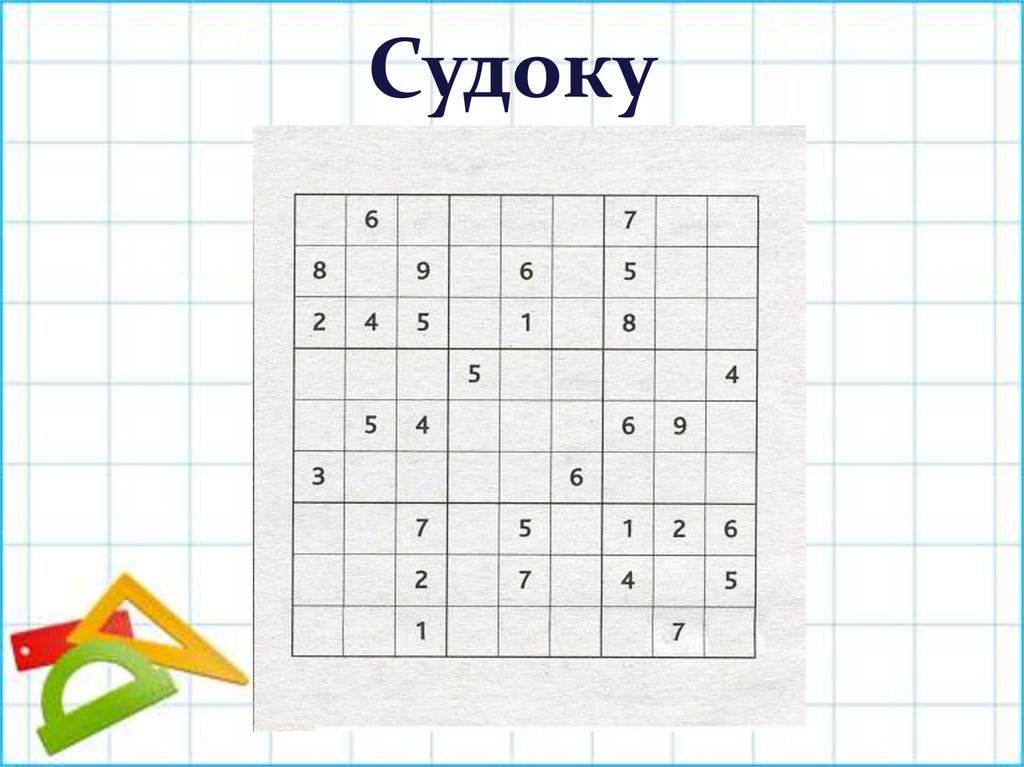
Судоку30.
НумерологияВеликий ученый Пифагор, считал, что всем на свете управляют числа.
Сущность человека заключается тоже в числе - дате его рождения. Он
создал метод построения квадрата, по которому можно познать характер
человека, состояние его здоровья, потенциальные возможности,
раскрыть достоинства и недостатки и выявить, что следует предпринять
для его совершенствования. Во времена Пифагора магические квадраты
на каждого человека создавались индивидуально.
Например, дата рождения 13.05.2002.
Цифра, которая встречается только один раз (или не встречается
вообще), говорит о том, что человеку в данной области необходимо
приложить некоторые усилия, чтобы улучшить ситуацию.
Две одинаковые цифры свидетельствуют о том, что это
качество развито у него сильнее, чем у большинства
людей. Это - его изюминка, козырь. Три и более
одинаковых цифры - показатель самой яркой черты
характера,
доминирующей
и
определяющей
жизненную позицию.
31.
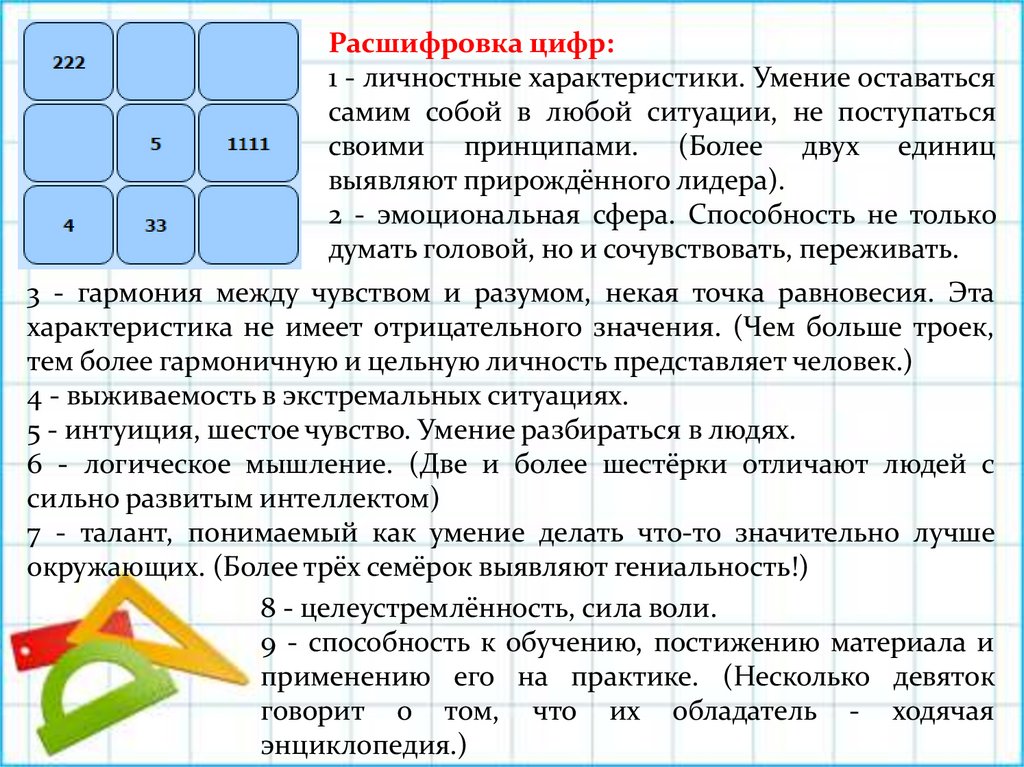
Расшифровка цифр:1 - личностные характеристики. Умение оставаться
самим собой в любой ситуации, не поступаться
своими принципами. (Более двух единиц
выявляют прирождённого лидера).
2 - эмоциональная сфера. Способность не только
думать головой, но и сочувствовать, переживать.
3 - гармония между чувством и разумом, некая точка равновесия. Эта
характеристика не имеет отрицательного значения. (Чем больше троек,
тем более гармоничную и цельную личность представляет человек.)
4 - выживаемость в экстремальных ситуациях.
5 - интуиция, шестое чувство. Умение разбираться в людях.
6 - логическое мышление. (Две и более шестёрки отличают людей с
сильно развитым интеллектом)
7 - талант, понимаемый как умение делать что-то значительно лучше
окружающих. (Более трёх семёрок выявляют гениальность!)
8 - целеустремлённость, сила воли.
9 - способность к обучению, постижению материала и
применению его на практике. (Несколько девяток
говорит о том, что их обладатель - ходячая
энциклопедия.)
32.
Алгоритм составления магическогоквадрата по дате рождения
Возьмём дату рождения: 23.08.2002. Сложим цифры дня, месяца и года
рождения (без нулей): 2+3+8+2+2=17. Далее складываем цифры
результата: 1+7=8. Затем из первой суммы вычитаем удвоенную первую
цифру дня рождения: 17-4=13. И вновь складываем цифры последнего
числа: 1+3=4. Получили числа 23.8.2002,17,8,13,4.
И составляем магический квадрат так, чтобы все единицы этих чисел
вошли в ячейку 1, все двойки – в ячейку 2 и т.д. Нули при этом во
внимание не принимаются.
11 222
4
7
88
33
33.
Результат1
1 – целеустремленность, воля, упорство, эгоизм.
1 – законченные эгоисты, стремятся из любого положения
извлечь максимальную выгоду.
11 – характер, близкий к эгоистическому.
111 – «золотая середина», Характер спокойный, покладистый,
коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким
характером подходят на роль военных – профессионалов, а
женщины держат семью в кулаке.
11111 – диктатор, самодур.
111111 – человек жестокий, способный
совершить невозможное; нередко попадает
под влияние какой-то идеи.
34.
Результат2
2
–
биоэнергетика,
эмоциональность,
душевность,
чувственность. Количество ячеек определяет уровень
биоэнергетики.
Двоек нет – открыт канал для интенсивного набора
биоэнергетики. Эти люди воспитаны и благородны от
природы.
2 – обычные в биоэнергетическом отношении люди. Такие
люди очень чувствительны к изменениям в атмосфере.
22 – относительно большой запас биоэнергетики. Из таких
людей получаются хорошие врачи, медсестры, санитары. В
семье таких людей редко у кого бывают нервные стрессы.
222 – знак экстрасенса.
35.
Результат3
3 – точность, конкретность, организованность, аккуратность,
пунктуальность, чистоплотность, скупость, наклонность к
постоянному «восстановлению справедливости».
Нарастание троек усиливает эти качества. С ними человеку есть
смысл искать себя в науках, особенно точных. Перевес троек
порождает педантов, людей в футляре.
4
4 – здоровье. Это связано с энергетическим пространством,
наработанным предками и защищающим человека. Отсутствие
четверок свидетельствует о болезненности человека.
4 – здоровье среднее, необходимо закалять организм. Из видов
спорта рекомендуется плавание и бег.
44 – здоровье крепкое.
444 и более – люди с очень крепким здоровьем.
36.
Результат5
5 – интуиция, ясновидение, начинающее проявляться у таких
людей уже на уровне трех пятерок.
Пятерок нет – канал связи с космосом закрыт. Эти люди
часто ошибаются.
5 – канал связи открыт. Эти люди могут правильно
рассчитать ситуацию, извлечь из нее максимальную пользу.
55 – сильно развита интуиция. Когда видят «вещие сны»,
могут предугадывать ход событий. Подходящие для них
профессии – юрист, следователь.
555 – почти ясновидящие.
5555 – ясновидящие.
37.
Результат6
6
–
заземленность,
материальность,
расчет,
склонность к
количественному освоению мира и недоверие к качественным скачкам и
тем более к чудесам духовного порядка. Шестерок нет – этим людям
необходим физический труд, хотя они его, как правило, не любят. Они
наделены неординарным воображением, фантазией, художественным
вкусом. Тонкие натуры, они тем не менее способны на поступок.
6 – могут заниматься творчеством или точными науками, но физический
труд является обязательным условием существования.
66 – люди заземлены, тянуться к физическому труду, хотя для них он не
обязателен; желательна умственная деятельность, занятия искусством.
666 – знак Сатаны, особый и зловещий знак. Эти люди обладают
повышенным темпераментом, обаятельны, неизменно становятся в
обществе центром внимания.
6666 – эти люди в своих предыдущих воплощениях
набрали слишком много заземленности, они очень много
трудились и не представляют свою жизнь без труда. Если в
их квадрате есть девятки, им нужно заниматься
умственной деятельностью, развивать интеллект.
38.
Результат7
7 – Мера таланта.
7 – чем больше люди работают, тем больше получают
впоследствии.
77 – очень одаренные, музыкальные люди, обладают тонким
художественным вкусом, могут иметь склонность к
изобразительному искусству.
777 – эти люди, как правило, приходят на землю ненадолго.
Они добры, безмятежны, болезненно воспринимают любую
несправедливость. Они чувствительны, любят мечтать, не
всегда чувствуют реальность.
7777 – знак Ангела. Люди с таким знаком
умирают в младенчестве, а если и живут, то их
жизни постоянно угрожает опасность.
39.
Результат8
8 – карма, долг, обязанность, ответственность. Количество
восьмерок определяет степень чувства долга.
Восьмерок нет – у этих людей почти полностью отсутствует
чувство долга.
8 – натуры ответственные, добросовестные, точные.
88 – у этих людей развито чувство долга, их всегда отличает
желание помочь другим, особенно слабым, больным,
одиноким.
888 – знак великого долга, знак служения народу. Правитель
с тремя восьмерками добивается выдающихся результатов.
8888 – обладают парапсихологическими
способностями
и
исключительной
восприимчивостью к точным наукам.
40.
Результат9
9 – ум, мудрость. Отсутствие девяток – свидетельство того, что
умственные способности крайне ограничены.
9 – эти люди должны всю жизнь упорно трудиться, чтобы
восполнить недостаток ума.
99 – эти люди умны от рождения. Учатся всегда неохотно, потому
что знания даются им легко. Они наделены чувством юмора с
ироничным оттенком, независимые.
999 – очень умны. К учению вообще не прикладывают никаких
усилий. Прекрасные собеседники.
9999 – этим людям открывается истина. Если у них к тому же
развита интуиция, то они гарантированы от провала в любом из
своих начинаний.



























 mathematics
mathematics








