Разметка и параметризация изображений. Лекция 11

1.

Обработка изображений в
системах управления
Лекция 11
Разметка и параметризация
изображений

2.

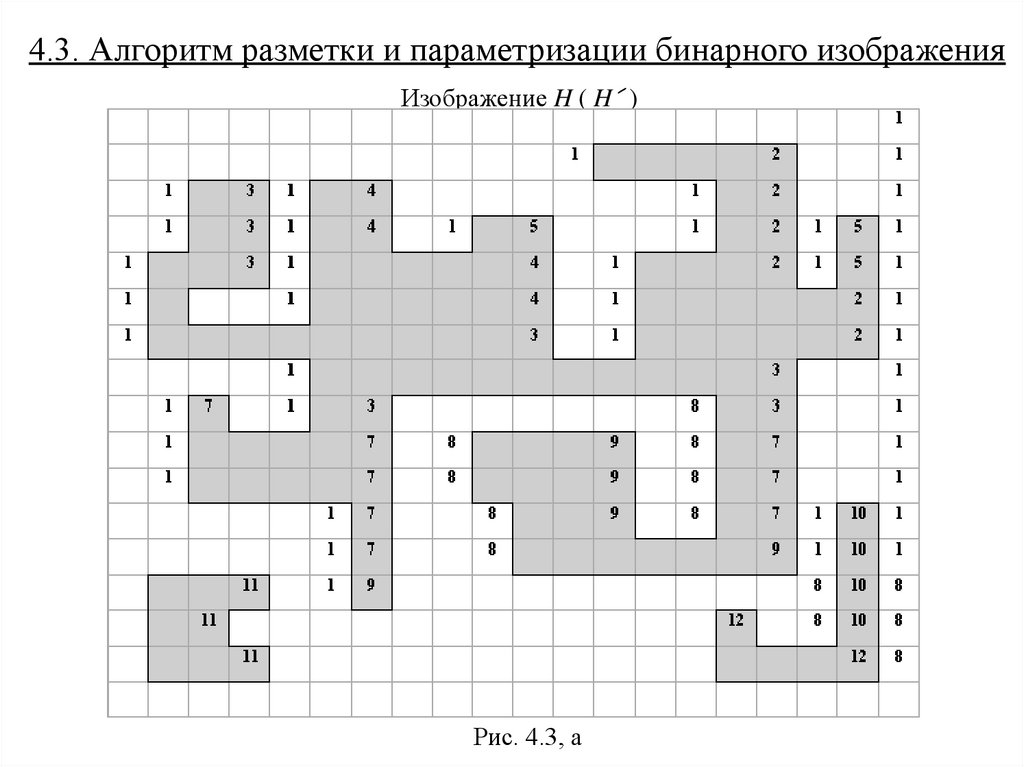
4.3. Алгоритм разметки и параметризации бинарного изображения
Изображение H ( H´ )
Рис. 4.3, а

3.

Строка (i-1)
p
g
li
r
k
Строка i
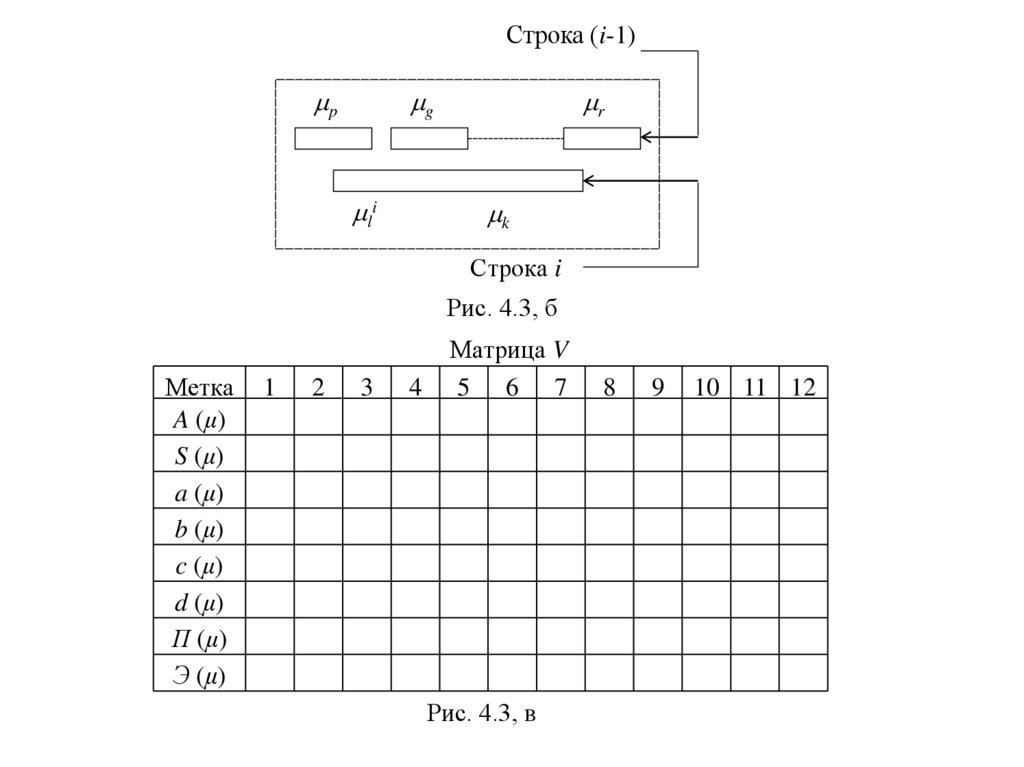
Рис. 4.3, б
Метка
A (μ)
S (μ)
a (μ)
b (μ)
c (μ)
d (μ)
П (μ)
Э (μ)
1
2
3
4
Матрица V
5 6 7
Рис. 4.3, в
8
9
10 11 12

4.

Вектор G
Номер элемента вектора
1
2
3
4
5
6
7
8
9
10 11 12 13
Исходное значение
элемента
Первичная метка
0
0
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
8
9
10 11 12
0
Метка-приемник
(прямой просмотр)
8
3
7
3
4
2
9
12
0
Метка приемник
отработанного вектора
8
9
9
9
9
9
9
8
9
0
12 11 12
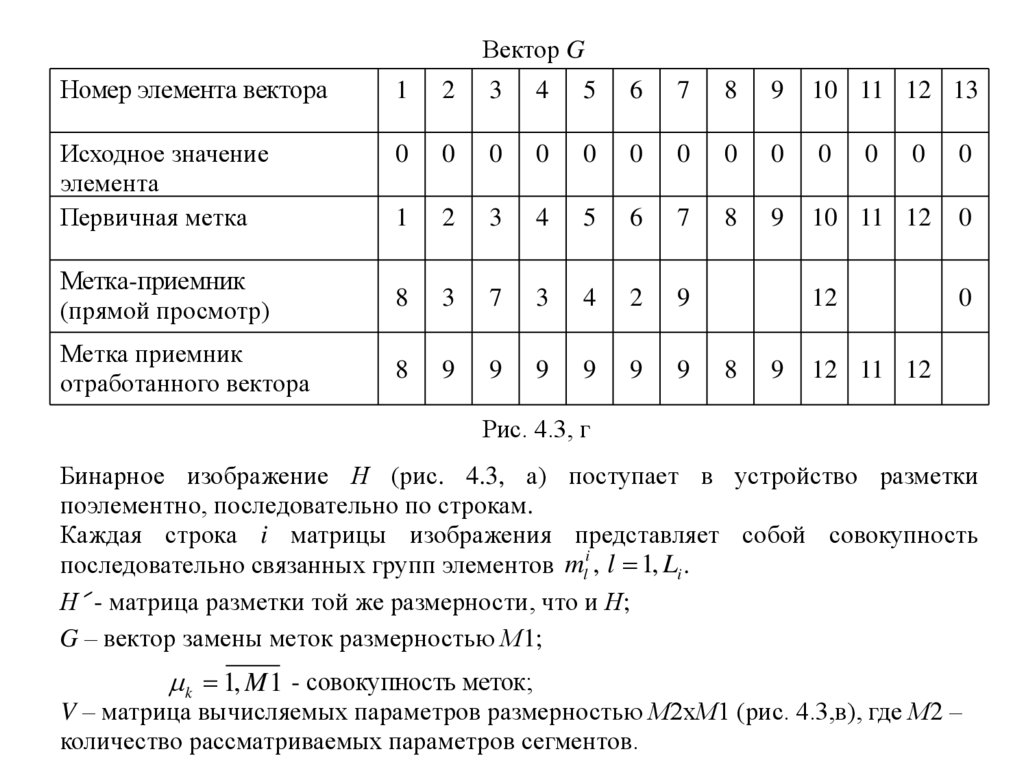
Рис. 4.3, г
Бинарное изображение Н (рис. 4.3, а) поступает в устройство разметки
поэлементно, последовательно по строкам.
Каждая строка i матрицы изображения представляет собой совокупность
последовательно связанных групп элементов mli , l 1, Li .
Н´ - матрица разметки той же размерности, что и Н;
G – вектор замены меток размерностью М1;
k 1, M 1 - совокупность меток;
V – матрица вычисляемых параметров размерностью М2хМ1 (рис. 4.3,в), где М2 –
количество рассматриваемых параметров сегментов.

5.

В качестве параметров сегментов примем следующие:
Ак – значение яркости (0 или 1) области изображения, помеченной меткой μk;
Sk – количество элементов;
ak, bk, ck, dk – левые, правые, верхние и нижние границы связной области, помеченной
меткой μk.
Процедура разметки реализуется в два этапа. На первом этапе в темпе поступления
изображения Н формируется матрица Н´, в которой каждой группе mli
последовательно связанных элементов изображения Н ставится в соответствие метка
μk(mli ), записываемая, например, по адресу последнего элемента группы. Каждая
метка является числом из натурального ряда целых чисел, т.е. μk = k, k=1,2,… .
Запись новых меток в матрицу Н´ производится с μr =1 в порядке возрастания.
Группа mli строки i, не имеющая связанных с нею групп строки (i–1), получает
новую метку. При этом в столбец μ ( mli ) записываются вычисляемые параметры
A,S, a, b, c, d группы связанных элементов mli и
по
адресу
вектора
G,
определяемому новой меткой, записывается значение данной метки. Если группа mli
связана с несколькими группами (i–1)-й строки, помеченными метками μр ,μq ,…, μr
(рис. 4.3, б), то при условии G(μp) = μр, G(μq) = μq,…, G(μr) = μr значение метки μk
принимается равным значению μp, т.е. метки первой из рассматриваемых групп (i–1)й строки. При этом элементы G(μq),…, G(μr) принимают значение метки μр, которая с
данного момента является меткой-приемником содержимого, определяемого метками
μq ,…, μr. Соответственно столбец μр матрицы V корректируется согласно
выражениям

6.

Sp = Sp + Sq + … + Sμ + Sk;
ap = min {ap, aq, …, ar, ak};
(4.27)
bp = max {bp, bq, …, br, bk};
cp = min {cp, cq, …, cr};
dp = i,
i
где Sk, ak, bk – параметры группы ml .
Если же среди меток μр ,…, μr фрагмента (рис.4.3,б) некоторые метки передали
содержимое и управление меткам-приемникам, т.е. для них не выполняется
условие G(μ)=μ, то такие метки сначала заменяются на их метки-приемники,
i
группе ml
присваивается первая по ходу строки (i–1) метка-приемник и она
же принимает содержимое остальных меток по правилу (4.27), что фиксируется
по соответствующим адресам вектора G.
Процедура определения метки-приемника μn при связывании групп элементов в
смежных строках определяется в соответствии с алгоритмом рис.4.4.
ввод μ
G(μ)=μ
нет
μ = G( μ)
Рис. 4.4
да
μn = μ
конец