Similar presentations:
Фильтрация изображений
1.
3 Фильтрация изображенийЦели обработки изображений
(1) улучшить качество изображения, опираясь на субъективное восприятие, обычно
увеличивая его контраст (image enhancement);
(2) улучшить качество изображения в объективной манере, например, уменьшив
размытость (image restoration);
(3) выделить определенные характеристики изображения, которые могут быть
использованы для идентификации его содержания (feature extraction).
(4) уменьшить количество бит для представления изображения с минимальным
искажением его контраста (image compression);
2.
3.
Например, усиление контраста можно рассматривать как процедуру улучшенияизображения, поскольку после ее применения изображение становится более приятным
для глаза, а обработку смазанных изображений отнести к арсеналу средств по
восстановлению изображений.
Рис.1. Изображения лейкоцитов
Рис.2. Удаление царапин с изображения
4.
3.2 Модели шумаБудем полагать, что модель искажения имеет вид
Слагаемое, описывающее шум в первом из уравнений неизвестно, поэтому вычесть его
невозможно. В случае периодического шума это иногда возможно сделать по спектру
изображения. На рис.3 показан процесс ухудшения изображения.
Рис.3
Часто полагают, что H тождественный оператор и искажения связаны с аддитивно
входящим шумом ( x, y )
Основные источники шума на изображении – это сам процесс его получения (внешние
условия съемки и качество датчиков) и процесс его передачи (помехи, возникающие в
каналах связи). Обычно предполагается, что шум не зависит от пространственных
координат и не коррелирует с самим изображением.
5.
Гауссов шумВозникает на изображениях в результате воздействия таких факторов, как шум в
электрических цепях, шум сенсоров из-за недостатка освещенности и/или высокой
температуры.
Шум Релея
Полезно при моделировании шума, на снимках снятых с большего расстояния.
6.
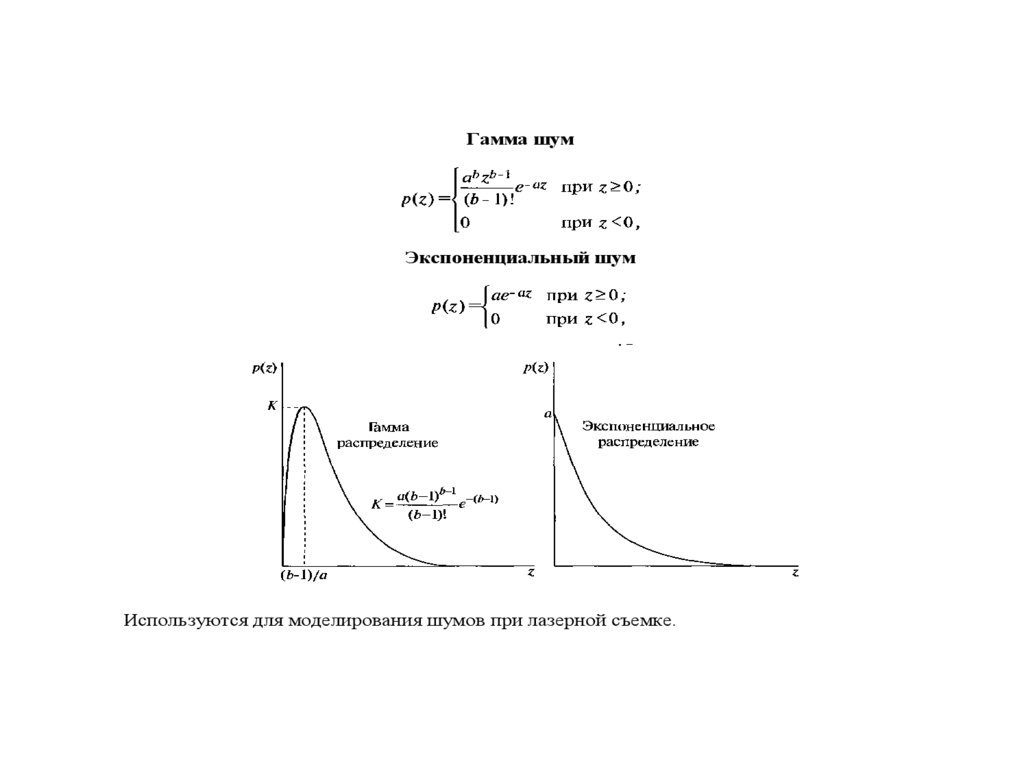
Гамма шумЭкспоненциальный шум
Используются для моделирования шумов при лазерной съемке.
7.
Равномерный шумРедко используется на практике.
Импульсный шум
a , Pa
b , Pb
f ( x, y )
f ( x, y ) , 1 - P - P
b
a
Возникают, когда в процессе получения изображения имеют место быстрые переходные
процессы.
8.
На рис.4 приведено тестовое изображение, а на рис.5 искаженные изображения. Тестовоеизображение состоит из простых областей постоянной яркости, которая принимает только
три значения и при этом охватывает весь диапазон от черного до белого.
Рис.4
9.
Рис.5Различия малозаметны за исключением изображений с импульсным шумом.
10.
Периодическийшум
возникает
при
интерференции
электрических
и
электромеханических процессов. С таким шумом можно справиться, используя частотную
фильтрацию. Часто используется модель вида
Рис.6. а) Изображение искаженное синусоидальным шумом различных
частот, б) спектр шума
Параметры
периодического
шума
можно
оценить,
анализируя
спектр
Фурье
изображения. Периодический шум порождает частотные всплески, которые можно
обнаружить даже визуально.
11.
12.
Часто бывает необходимо оценить параметры шума непосредственно по зашумленномуизображению или по набору таких изображений. В этом случае следует выбрать на
некотором изображении область, по возможности лишенную характерных черт, чтобы
распределение яркости на ней было бы произведено главным образом шумом.
Рис.7. а) Зашумленное изображение, б) Область,
в) Гистограмма области, г) Гистограмма
гауссова шума (сгенерированная)
13.
3.3 Пространственная фильтрацияОкрестностная обработка изображений состоит из следующих действий:
A) определение центральной точки ( x, y ) ;
B) совершение операции, которая использует лишь значения пикселов в заранее
оговоренной окрестности вокруг центральной точки;
C) назначение результата этой операции «откликом» совершаемого процесса в
этой точке;
D) повторение всего процесса для каждой точки изображения.
В результате перемещения центральной точки образуются новые окрестности,
отвечающие каждому пикселу изображения. Для описанной процедуры принято
использовать термин пространственная фильтрация. Если операции, совершаемые над
пикселами окрестности, являются линейными, то вся процедура называется линейной
пространственной фильтрацией, в противном случае она называется нелинейной
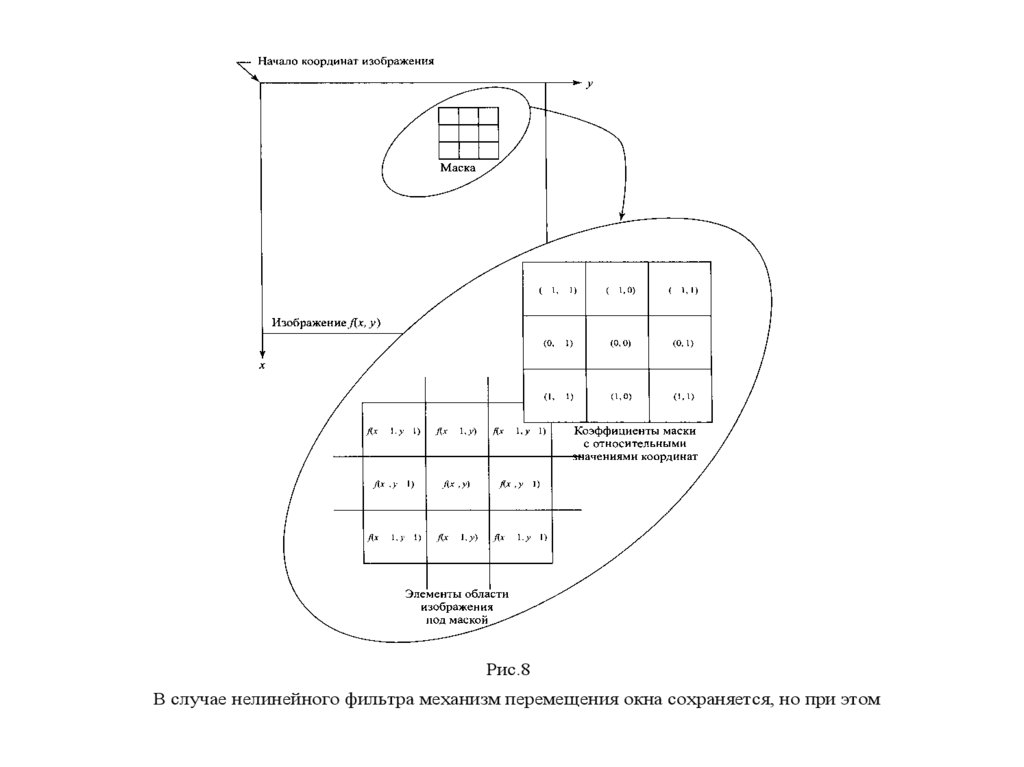
пространственной фильтрацией. Описанная процедура иллюстрируется на рис.8.
Алгоритм основан на перемещении маски фильтра от точки к точке.
14.
Рис.8В случае нелинейного фильтра механизм перемещения окна сохраняется, но при этом
15.
В случае линейного фильтра и маски 3х3 результат определяется выражениемВ случае фильтрации изображения M N с маской m т алгоритм определяется
выражением
где a (m 1) / 2, b (n 1) / 2, x 0,1,..., M 1, y 0,1,..., N 1 . Иногда используется и
другое обозначение
с маской 3 3
В случае нелинейного фильтра механизм перемещения окна сохраняется, но при этом
используются нелинейные преобразования пикселов.
16.
Линейные сглаживающие фильтрыПрименяются для расфокусировки изображения и подавления шума. Расфокусировка
может применяться, например, для удаления мелких деталей перед обнаружением
больших объектов или для устранения разрывов в линиях или деталях.
фильтров
представляет
собой
среднее
значение
элементов
Выход таких
окрестности.
Заменой
исходных значений на средние по окрестности достигается уменьшение резких переходов
уровней яркости. Так как шум характеризуется такими скачками, то наиболее очевидное
применение это подавление шумов. Однако при этом происходит расфокусировка
контуров изображения, которые также характеризуются перепадами яркостей. Главное
применение это подавление несущественных деталей, совокупностей пикселей, которые
малы по сравнению с маской.
Рис.9
Коэффициент в центре маски имеет максимальное значение. Такая маска дает средне
взвешенное значение отклика. Общее представление для алгоритма сглаживания
17.
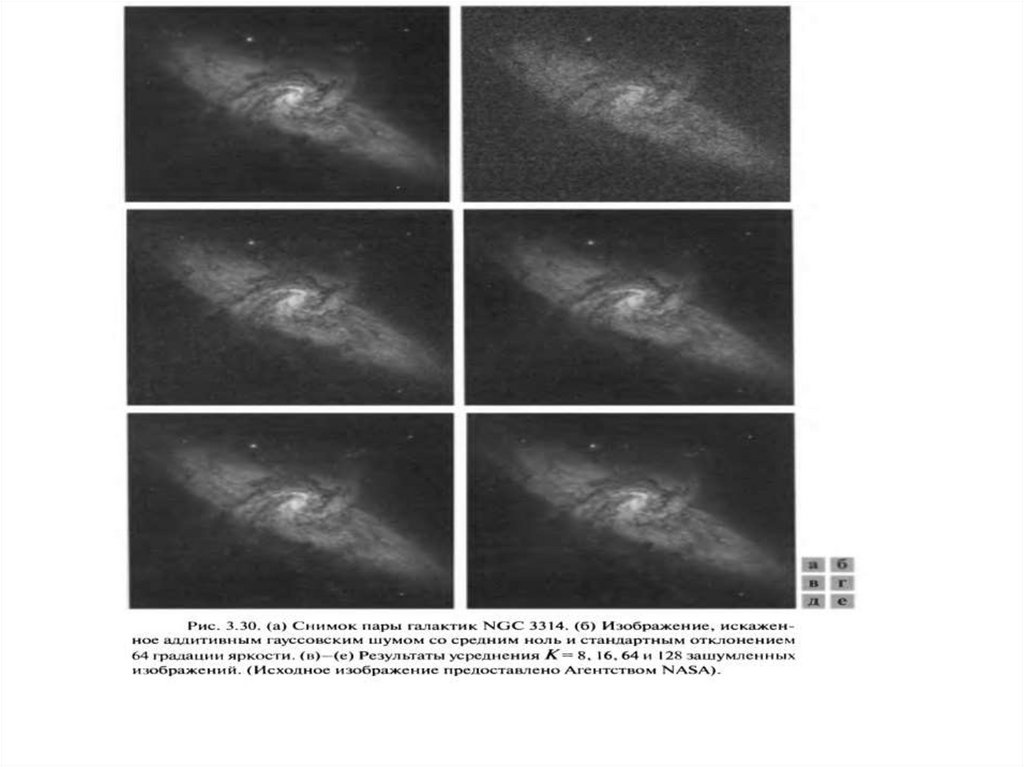
Уменьшение шума усреднением18.
19.
20.
На рис.10 приведены результаты сглаживания фильтрами порядка 3, 9, 15, 35.Рис.10
21.
На рис.11 показаны результаты обработки фильтром 15х15 изображения, полученногос телескопа Хаббл.
Рис.11
Рис. 12 (Сверху слева) идеальное изображение шахматной доски, на котором
значения пикселов в черных клетках равны 0, а значения пикселов в белых клетках равны255. (Сверху в центре) изображение с добавленным гауссовым шумом
со среднеквадратическим отклонением 30. (Сверху справа) диаграмма значений
интенсивности пикселов из 100-й сверху горизонтальной строки зашумленного
изображения.
22.
Вместо присвоения всем пикселам фильтра равных весов предпочтительнеевыбрать веса такими, чтобы они уменьшались с увеличением расстояния входных
пикселов от центрального пиксела I[xc, yc]. Подобные весовые коэффициенты имеет
фильтр Гаусса, который, возможно, является наиболее широко используемым фильтром.
При применении фильтра Гаусса значение пиксела [x, y] взвешивается с использованием
весовой функции
( x x0 ) 2 ( y y 0 ) 2
1
W ( x, y)
exp(
2
2 2
(x − xc)2 + (y − yc)2 представляет расстояние пиксела [x, y] от центрального пиксела
окрестности [xc, yc] на выходном изображении, для формирования которого применяется
фильтр.
23.
24.
Нелинейная пространственная фильтрацияНелинейная
пространственная
фильтрация
также
основана
на
окрестностных
операциях, причем механизм определения окрестности размера и скольжения ее центра по
изображению является таким же, как и в линейной фильтрации, описанной в предыдущем
параграфе. Однако там, где линейная фильтрация использует сумму произведений (т.е.
линейную операцию), нелинейная фильтрация основана (что следует из ее названия) на
нелинейных операциях, совершаемых над пикселами текущей окрестности. Например,
если положить, что отклик фильтра в каждой центральной точке равен максимальному
значению в ее окрестности, то это определит нелинейную операцию фильтрации.
Наиболее известен медианный фильтр, который заменяет значение пикселя на
значение медианы распределения всех пикселей окрестности. Подавляют импульсные
шумы
при
существенно
меньшей
расфокусировке,
чем
линейные
фильтры.
Изолированные темные или светлые кластеры, имеющие площадь не более половины
площади маски будут удалены. При этом кластеры больших размеров искажаются
существенно меньше.
25.
Рис. 5.8. (Слева) зашумленное изображение шахматной доски. (В центре) результат обработки посредством присвоения каждому выходному пикселу значения медианой окрестности 5 × 5 пикселов с центром в соответствующем пикселе входногоизображения. (Справа) значения пикселов из 100-й сверху горизонтальной строки
изображения.
Рис. 5.9. (Слева) входное изображение содержит гауссов шум и ложные детали в
виде ярких окружностей, которые были добавлены к четырем ранее однородным
областям. (Справа) результат применения медианного фильтра с маской размера
7×7.
26.
Использование 100-й процентили приводит к фильтру максимума, который полезенпри поиске на изображении наиболее ярких точек
Нулевая процентиль используется для отыскания противоположных значений.
На рис.12 показаны результаты обработки рентгеновского снимка монтажной платы
сглаживающим и медианным фильтрами 3х3.
Рис.12
27.
Для подавления шума часто используются следующие пространственные фильтры.1. Основанный на вычислении среднеарифметического
2. Основанный на вычислении среднего геометрического
Приводит к сглаживанию, сравнимому с предыдущим фильтром, но при этом
теряется меньше деталей.
28.
Рис.13. а) Рентгеновский снимок, б) Рентгеновский снимок, искаженный шумом,в) использование среднеарифметического фильтра 3*3,
г) использование среднегеометрического фильтра 3*3.
29.
3. Основанный на вычислении среднего гармоническогоХорошо работает в случае униполярного белого импульсного шума и гауссовского
шума. Не работает при черном импульсном шуме.
4. Основанный на вычислении среднего контргармонического
где Q называется порядком фильтра. Позволяет уменьшить импульсный шум. При
Q > 0 подавляет черную составляющую шума, при Q < 0 – белую.
30.
Рис.15. Результат неправильного выбора QРис.14. а) Изображение, искаженное черным импульсным шумом с вероятностью
0.1,
б) Изображение, искаженное белым импульсным шумом с вероятностью 0.1
в) Результат фильтрации с Q=1.5 и маской 3*3,
г) Результат фильтрации с Q=-1.5 и маской 3*3,
31.
Пример.Рис.16. а) Результат фильтрации изображения 8 а) фильтром максимума
с маской 3*3 , б) Результат фильтрации изображения 8 в) фильтром минимума с
маской 3*3.
32.
33.
Адаптивные пространственные фильтрыПриведенные выше фильтры применяются одинаково ко всем пикселам изображения
независимо от их местоположения. В некоторых случаях результат фильтрации можно
улучшить, если фильтр имеет возможность менять свое действие в зависимости от
характеристик изображения в области фильтрации
34.
Пример.Рис.17. а) Изображение, искаженное гауссовским шумом, б) Использование
среднеарифметического фильтра 7*7, в) Использование среднегеометрического
фильтра 7*7, в) Использование адаптивного фильтра фильтра 7*7.
35.
Частотная фильтрацияДискретное прямое и обратное преобразования Фурье
Прямое размерами M N :
где u 0,1,..., M 1, v 0,1,..., N 1 .
Обратное размерами M N :
где x 0,1,..., M 1, y 0,1,..., N 1 .
u, v ˗ частотные переменные, x, y ˗ пространственные переменные.
Спектр, фаза и энергетический спектр определяются выражениями
.
36.
Модель сигнала в частотной областиОбычно предварительно домножают изображение на функцию ( 1) x y
Так как
то значение Фурье преобразования в начале координат равно среднему значению яркости
исходного изображения (постоянная составляющая).
Каждый элемент ПФ F (u, v) содержит все отсчеты f ( x, y ) , умноженные на значения
экспонент. Поэтому не следует ожидать, что прямого соответствия между характером
изображения и его образа. Однако некоторые утверждения общего характера
относительно их взаимосвязи могут быть сделаны.
1. Частота связана с вариацией яркости изображения. Поэтому интуитивно ясно, что
частоты в ПФ связаны с ней.
2. Постоянная составляющая совпадает со средней яркостью изображения.
3. Низкие частоты в начале координат соответствуют медленно меняющимся
компонентам изображения.
4. По мере удаления от начала координат, более высокие частоты соответствуют все
более резким изменениям яркости изображения, которые соответствуют границам
и другим деталям.
37.
Рис.10. Увеличенное изображение в 2500 раз поврежденноймикросхемы и ее ФП
38.
39.
Рис.11. Этапы фильтрации40.
Основные фильтры и их свойства1. Фильтр Пробка.
Служит для обнуления в частотной области среднего значения на изображении.
Определяется выражением
Рис.12. Увеличенное изображение в 2500 раз поврежденной
микросхемы и фильтрованное изображение
41.
Низкочастотные фильтрыПример.
y t st t
s t ̶ полезный сигнал, t ̶ помеха. Диапазоны спектров сигналы и помехи не
пересекаются. Требуется сконструировать линейный фильтр (рис.1), который подавлял бы
помеху.
Рис.2
Фильтр разыскивается в классе линейных устойчивых звеньев с передаточной
функцией
W ( p)
B( p )
.
D( p )
42.
Пример.yt sin( 2 10t ) sin( 2 20t ) .
43.
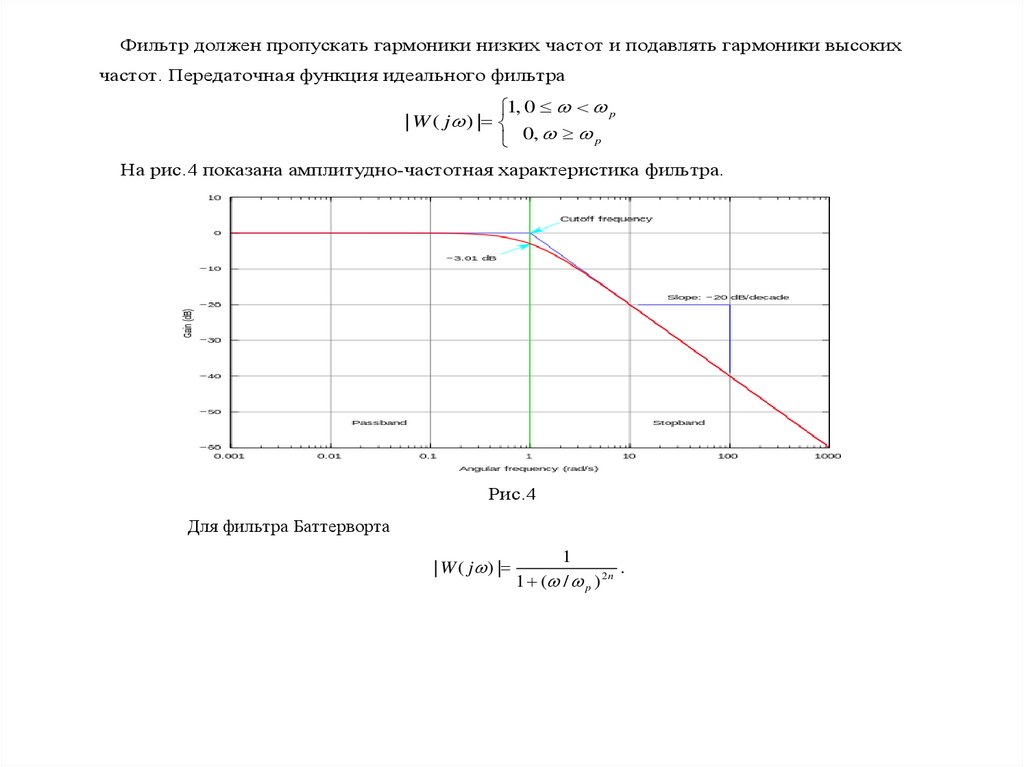
Фильтр должен пропускать гармоники низких частот и подавлять гармоники высокихчастот. Передаточная функция идеального фильтра
1, 0 p
| W ( j ) |
0, p
На рис.4 показана амплитудно-частотная характеристика фильтра.
Рис.4
Для фильтра Баттерворта
| W ( j ) |
1
.
1 ( / p ) 2 n
44.
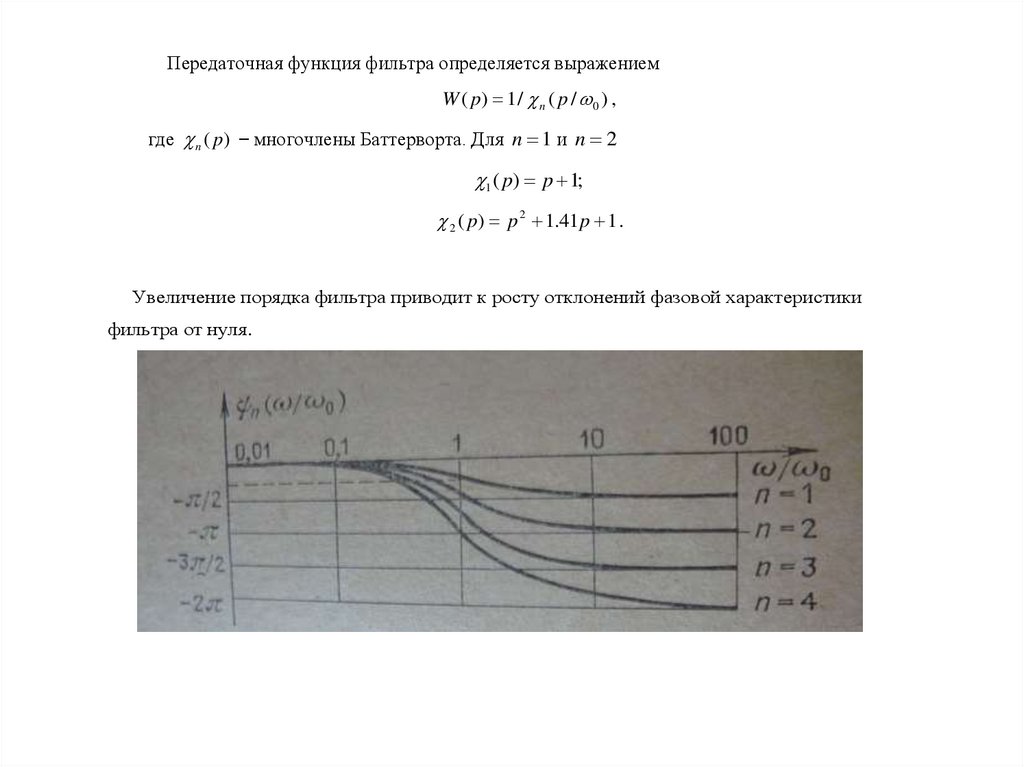
Передаточная функция фильтра определяется выражениемW ( p) 1 / n ( p / 0 ) ,
где n ( p) ̶ многочлены Баттерворта. Для n 1 и n 2
1 ( p) p 1;
2 ( p) p 2 1.41 p 1 .
Увеличение порядка фильтра приводит к росту отклонений фазовой характеристики
фильтра от нуля.
45.
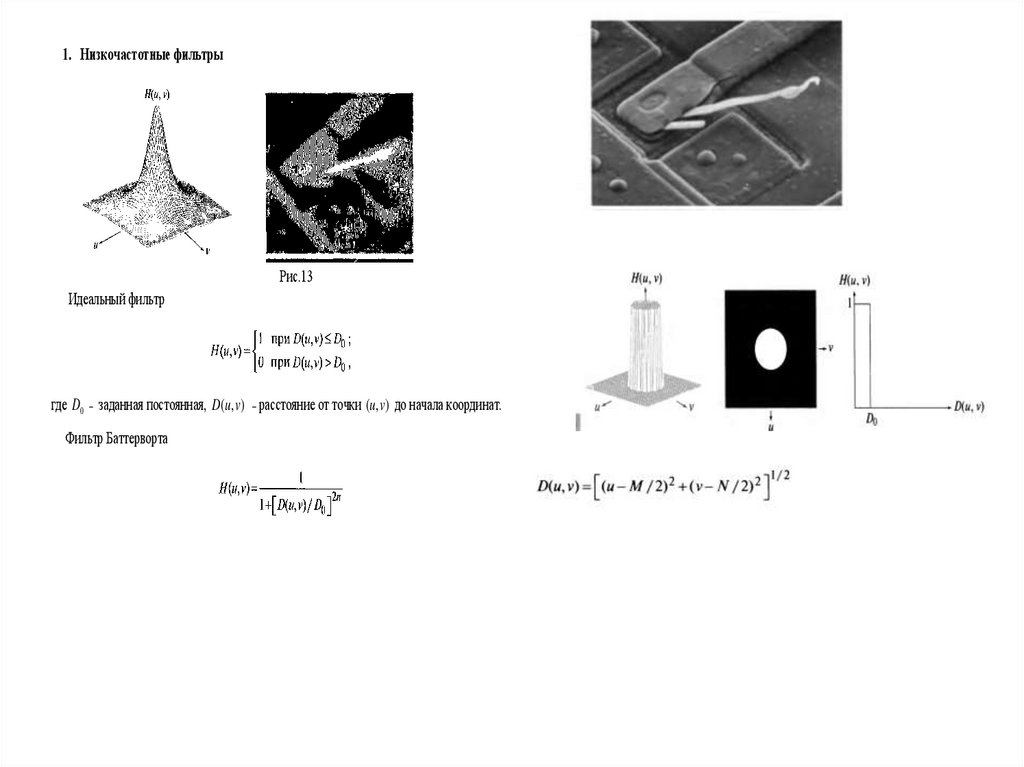
1. Низкочастотные фильтрыРис.13
Идеальный фильтр
где D0 ˗ заданная постоянная, D(u, v) ˗ расстояние от точки (u, v) до начала координат.
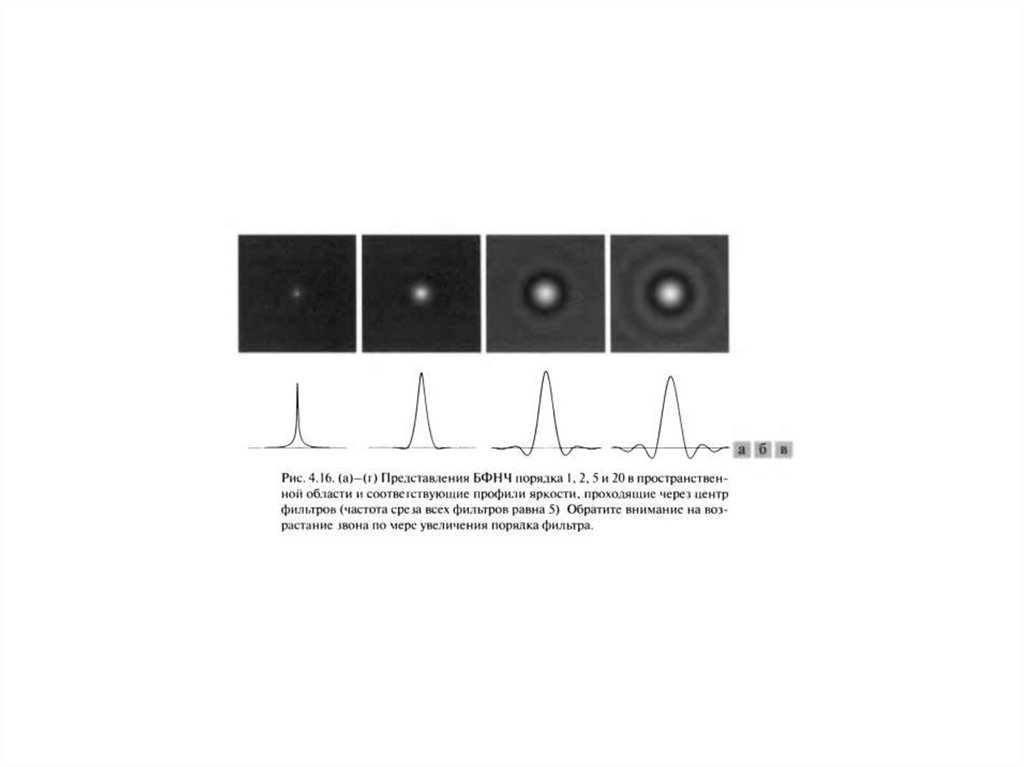
Фильтр Баттерворта
46.
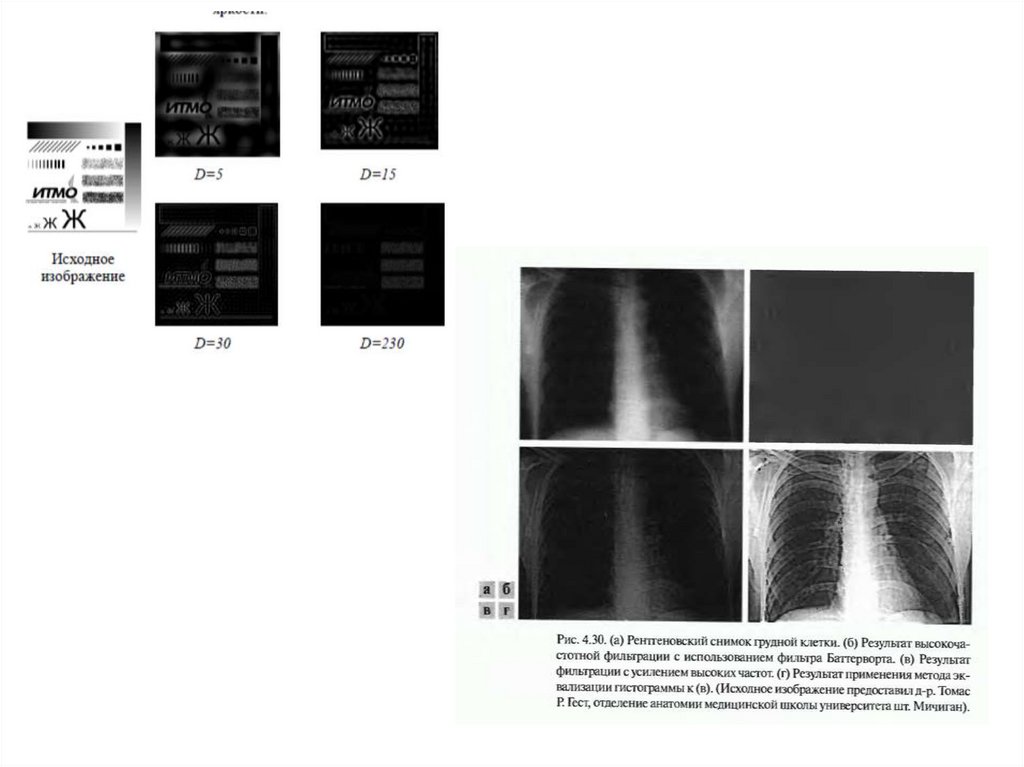
Пример.47.
48.
49.
50.
Рис.14. Образец текста и результат фильтрации51.
1. Высокочастотная фильтрацияРис.15. Увеличенное изображение в 2500 раз поврежденной
микросхемы и фильтрованное изображение
Идеальный фильтр
Фильтр Баттерворта
















































 informatics
informatics








