Similar presentations:
Задания №24-25. Подготовка к ОГЭ по геометрии
1.
13.05.21Классная работа
Подготовка к ОГЭ. Задания №24-25
2. Цели урока:
- Закрепить умениевыполнять задания
типа 24-25.
- Развивать умение анализировать,
сравнивать, обобщать.
- Продолжить
формирование культуры
устной и письменной речи, умения
оценивать уровень своих знаний.
3.
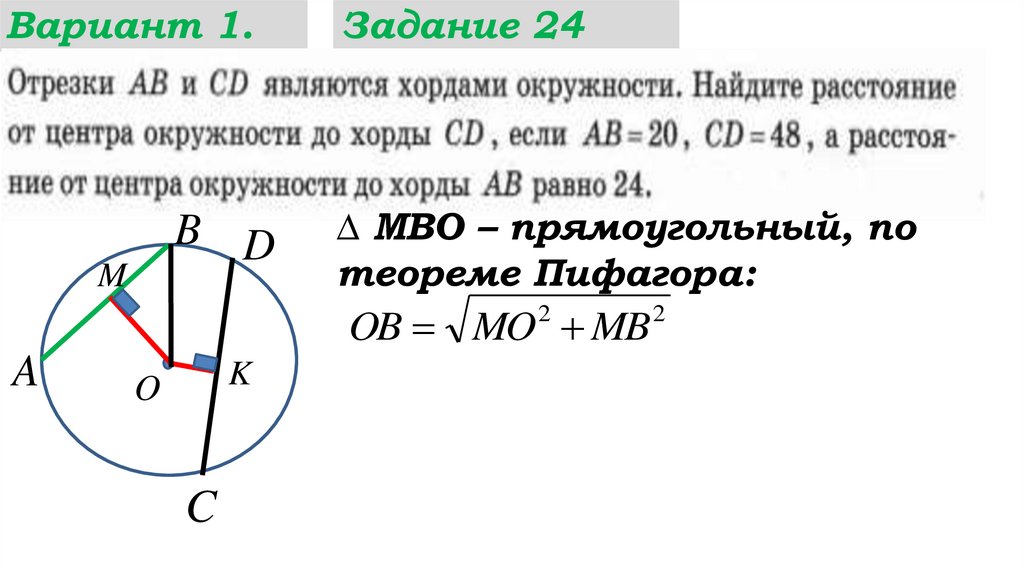
Вариант 1.Задание 24
Выполните чертёж
4.
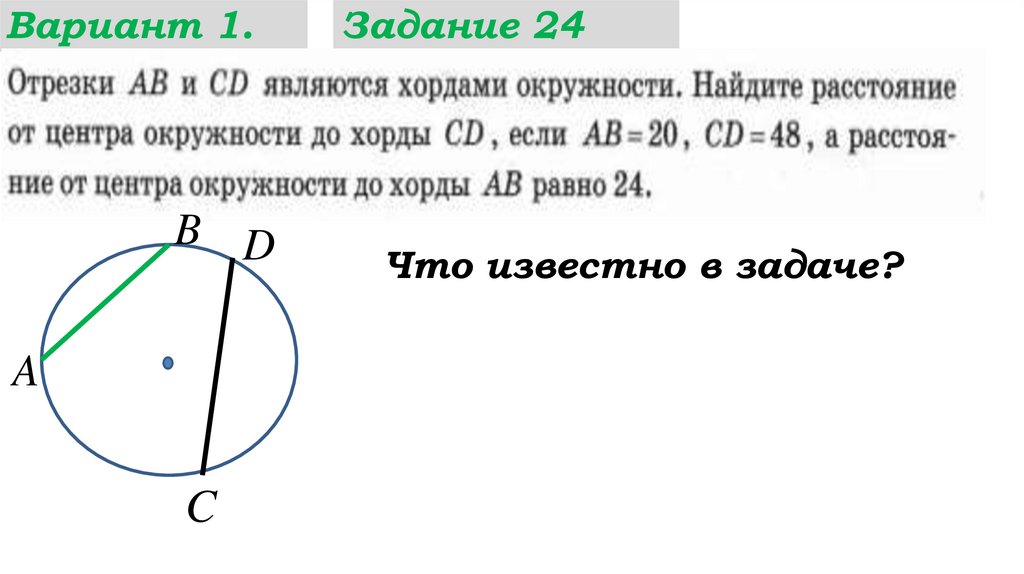
Вариант 1.B D
A
C
Задание 24
Что известно в задаче?
5.
Вариант 1.20
B D
48
A
C
Задание 24
Покажите расстояние от
центра окружности до
хорды АВ ( до хорды CD)
6.
Вариант 1.B D
M
A
K
O
C
Задание 24
Какими являются хорда АВ и
отрезок ОМ?
хорда CD и отрезок ОК?
7.
Вариант 1.B D
M
A
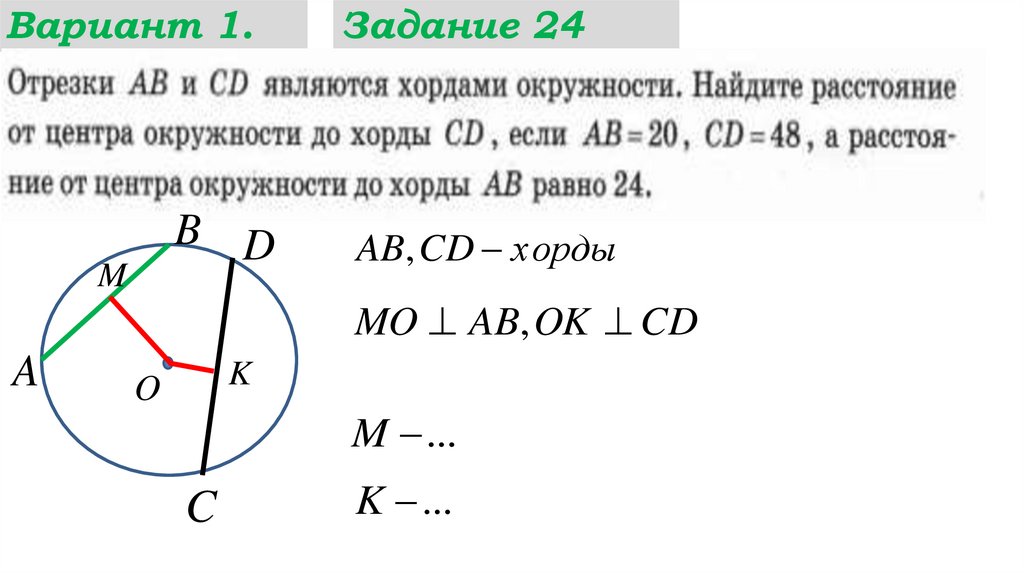
Задание 24
AB, CD хорды
MO AB, OK CD
K
O
M ...
C
K ...
8.
Вариант 1.B D
M
A
K
O
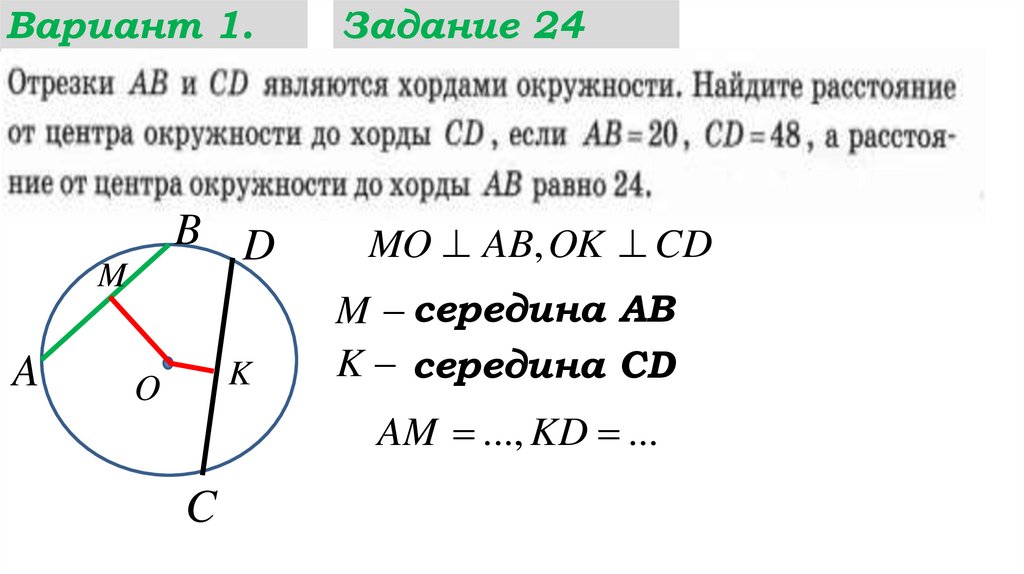
Задание 24
MO AB, OK CD
M середина АВ
K середина CD
AM ..., KD ...
C
9.
Вариант 1.B D
M
A
K
O
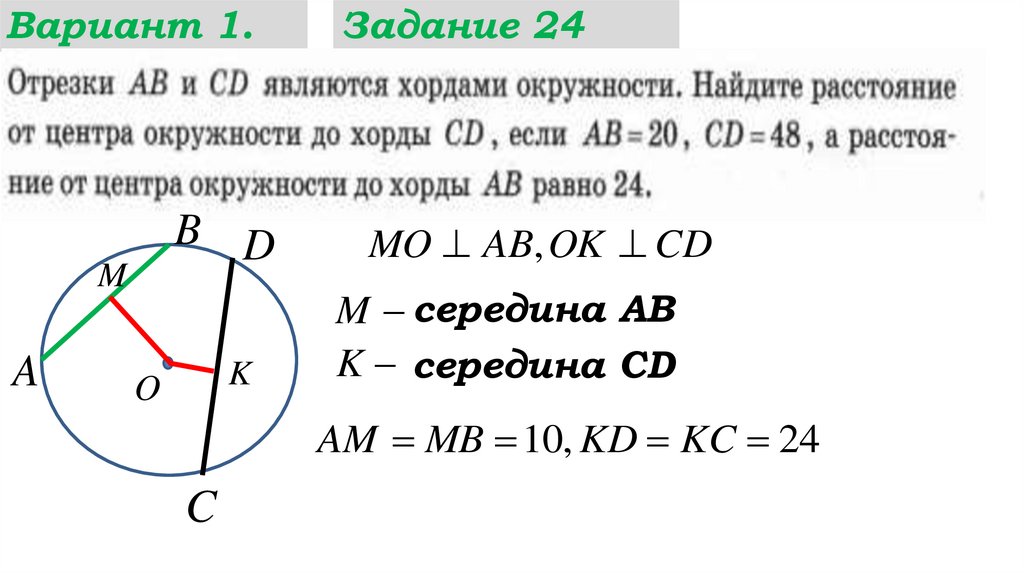
Задание 24
MO AB, OK CD
M середина АВ
K середина CD
AM MB 10, KD KC 24
C
10.
Вариант 1.B D
M
A
K
O
C
Задание 24
Назовите треугольник, в
котором можно назвать
длины двух его сторон?
11.
Вариант 1.B D
M
A
K
O
C
Задание 24
Дайте характеристику
треугольника МВО и укажите
что можно в нём найти
12.
Вариант 1.B D
M
Задание 24
∆ МВО – прямоугольный, по
теореме Пифагора:
OB MO MB
2
A
K
O
C
2
13.
Вариант 1.B D
M
Задание 24
∆ МВО – прямоугольный, по
теореме Пифагора:
OB MO MB
2
2
OB 10 24 26
2
A
K
O
C
2
Дайте характеристику
треугольника KDО и укажите что
можно в нём найти
14.
Вариант 1.B D
M
A
K
O
C
Задание 24
∆ МВО – прямоугольный, по теореме
2
2
Пифагора:
OB MO MB
2
2
OB 10 24 26
∆ KDO – прямоугольный, по теореме
Пифагора:
15.
Вариант 1.B D
M
A
K
O
Задание 24
∆ МВО – прямоугольный, по теореме
2
2
Пифагора:
OB MO MB
2
2
OB 10 24 26
∆ KDO – прямоугольный, по теореме
Пифагора:
OK DO KD
2
C
2
16.
Вариант 1.B
M
A
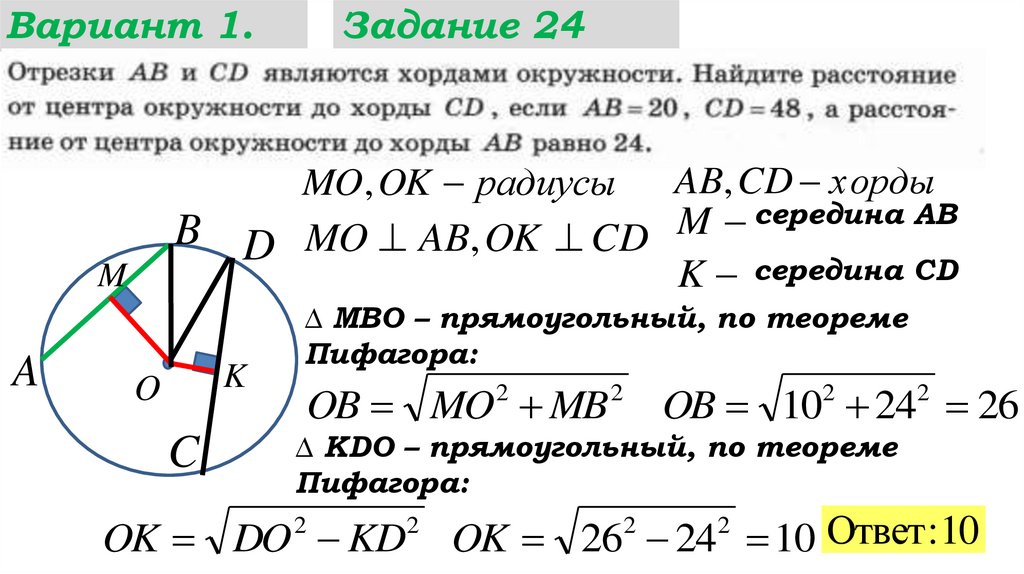
MO, OK радиусы AB, CD хорды
середина АВ
M
D MO AB, OK CD
K середина CD
K
O
C
Задание 24
∆ МВО – прямоугольный, по теореме
Пифагора:
OB MO MB
2
OB 10 24 26
2
2
2
∆ KDO – прямоугольный, по теореме
Пифагора:
OK DO KD
2
2
OK 26 24 10 Ответ :10
2
2
17.
Вариант 1.Задание 25
Выполните чертёж
18.
Вариант 1.В
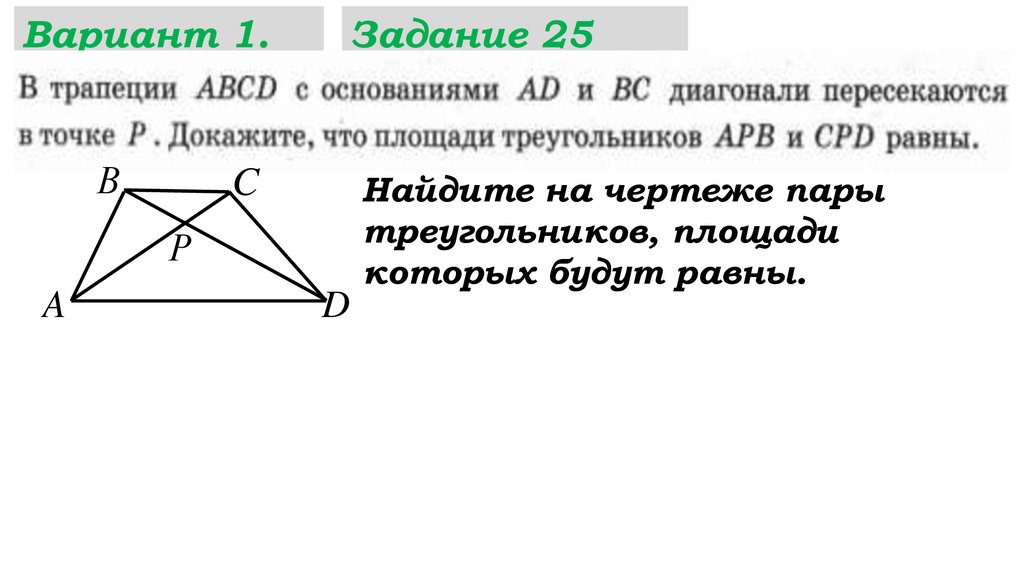
Задание 25
C
Р
A
D
Найдите на чертеже пары
треугольников, площади
которых будут равны.
19.
Вариант 1.В
C
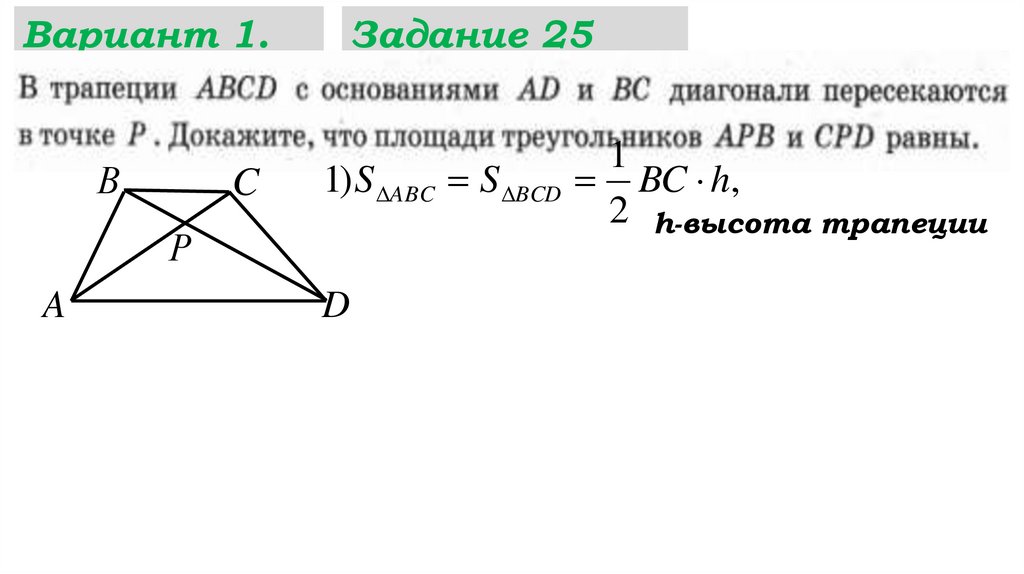
Задание 25
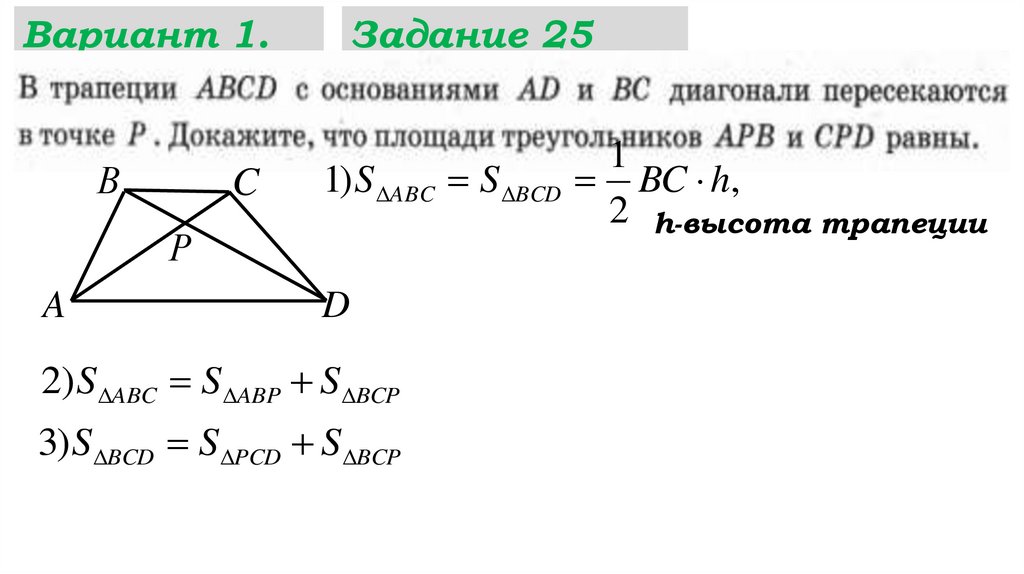
1) S ABC S BCD
Р
A
D
1
BC h,
2 h-высота трапеции
20.
Вариант 1.В
C
Задание 25
1) S ABC S BCD
Р
A
D
2) S ABC S ABP S BCP
3)S BCD S PCD S BCP
1
BC h,
2 h-высота трапеции
21.
Вариант 1.В
Задание 25
1) S ABC S BCD
C
Р
A
1
BC h,
2
h-высота трапеции
D
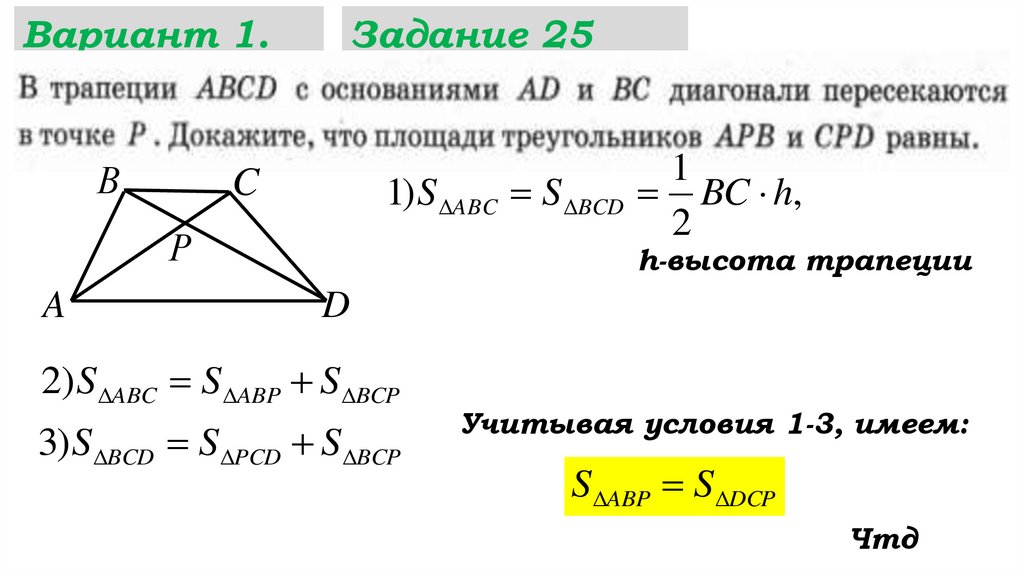
2) S ABC S ABP S BCP
3)S BCD S PCD S BCP
Учитывая условия 1-3, имеем:
S ABP S DCP
Чтд
22.
Вариант 6.Задание 24
Подумайте как обозначить трапецию.
Выполните чертёж, отметьте все
данные
23.
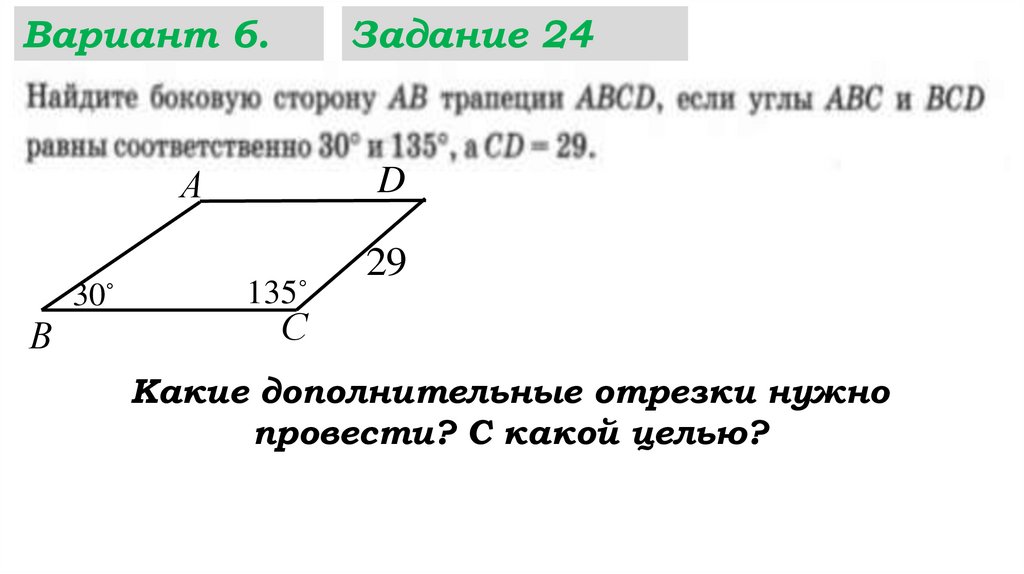
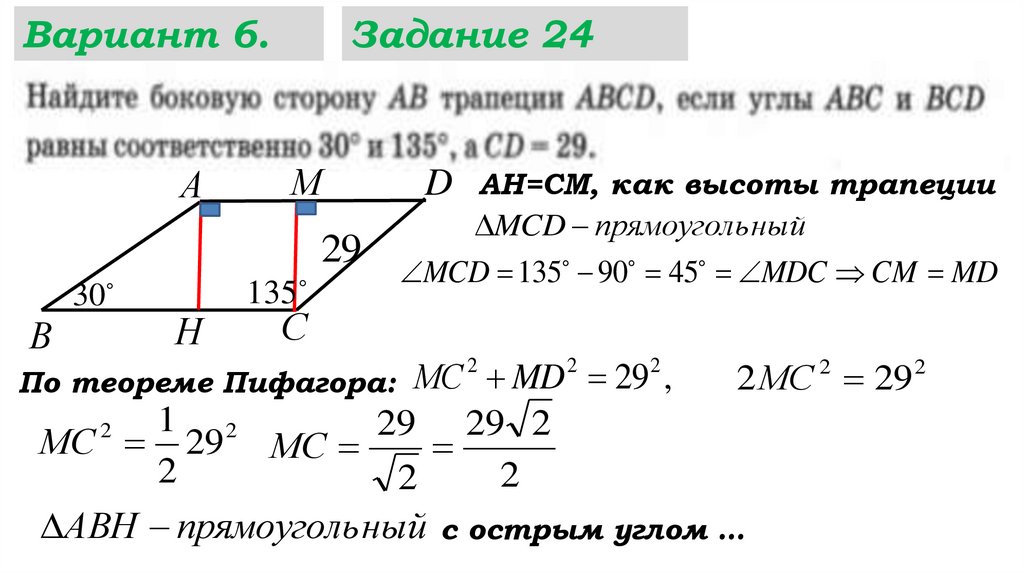
Вариант 6.Задание 24
А
30
В
D
135
29
С
Какие дополнительные отрезки нужно
провести? С какой целью?
24.
Вариант 6.А
30
В
Н
Задание 24
М
135
D
29
С
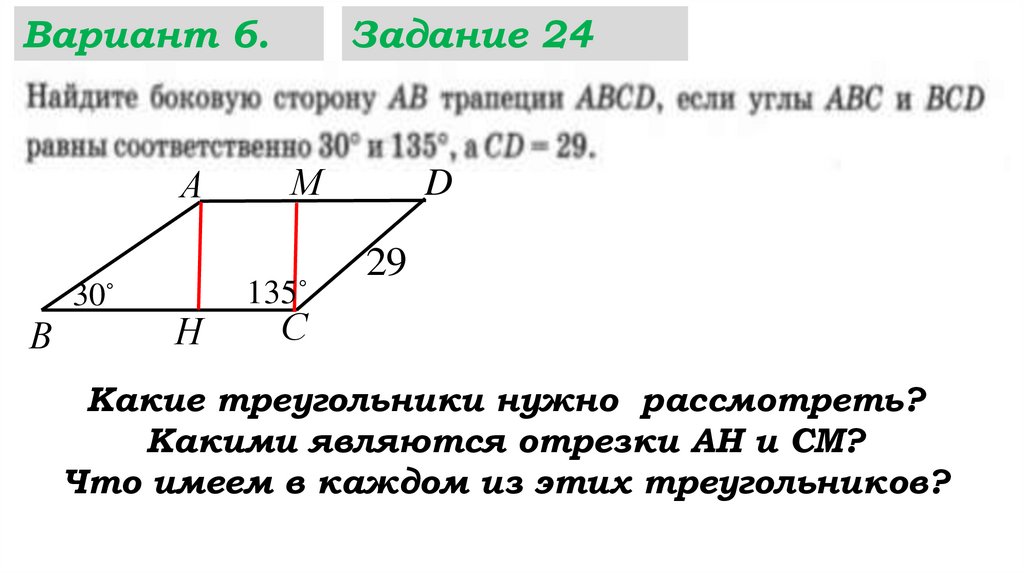
Какие треугольники нужно рассмотреть?
Какими являются отрезки АН и СМ?
Что имеем в каждом из этих треугольников?
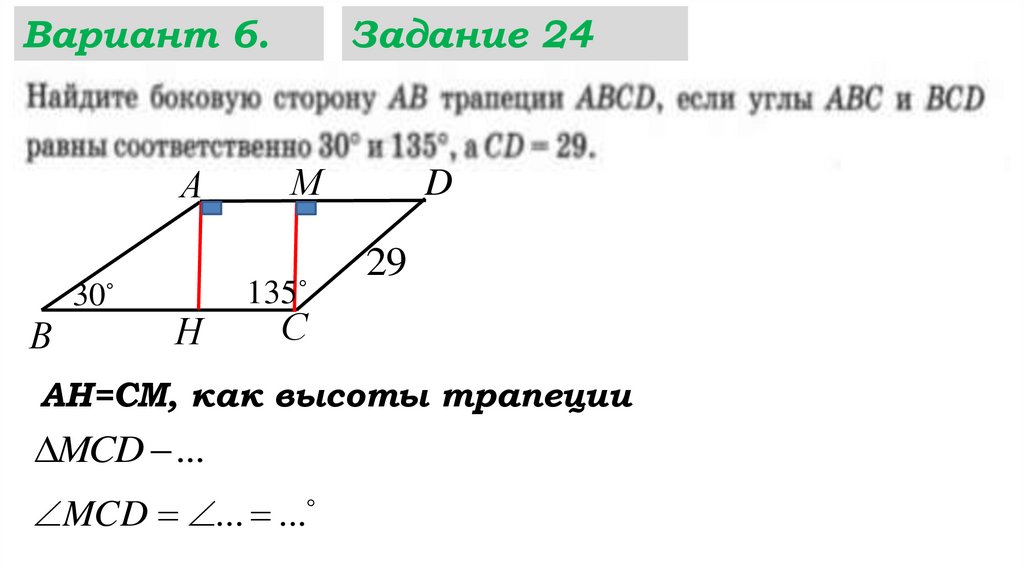
25.
Вариант 6.А
30
В
Н
Задание 24
М
135
D
29
С
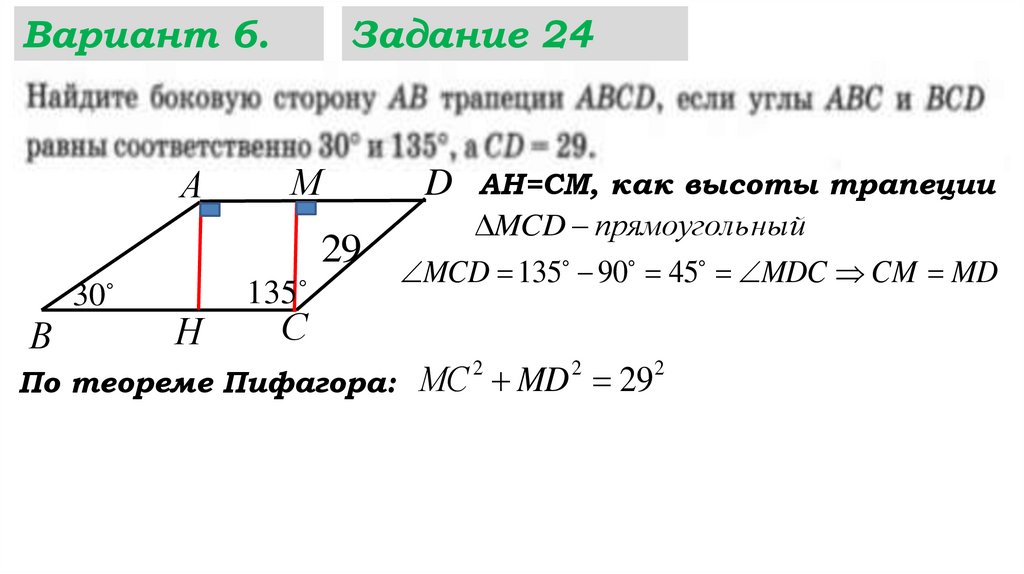
АН=СМ, как высоты трапеции
MCD ...
MCD ... ...
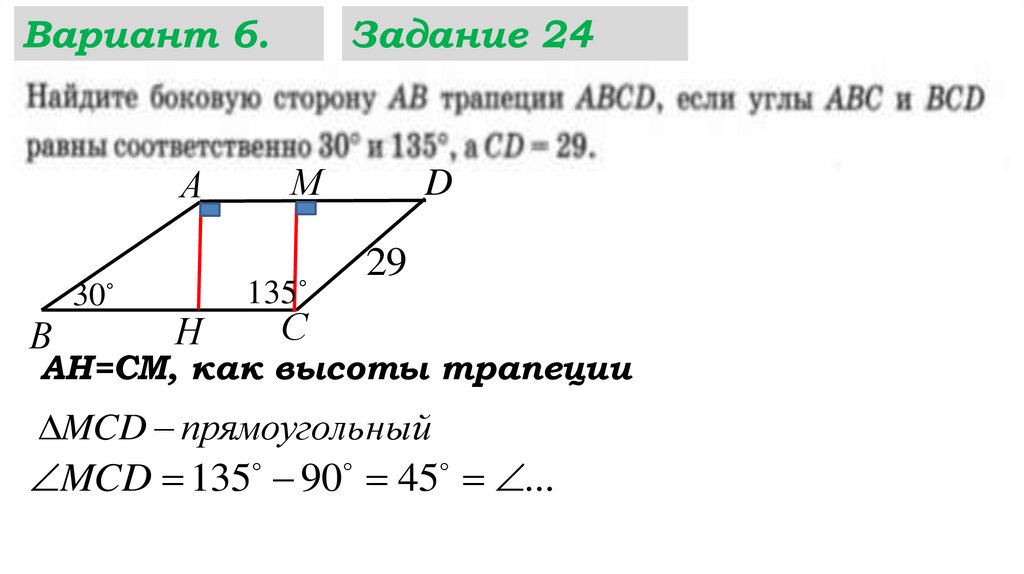
26.
Вариант 6.М
А
30
В
Н
Задание 24
135
D
29
С
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 ...
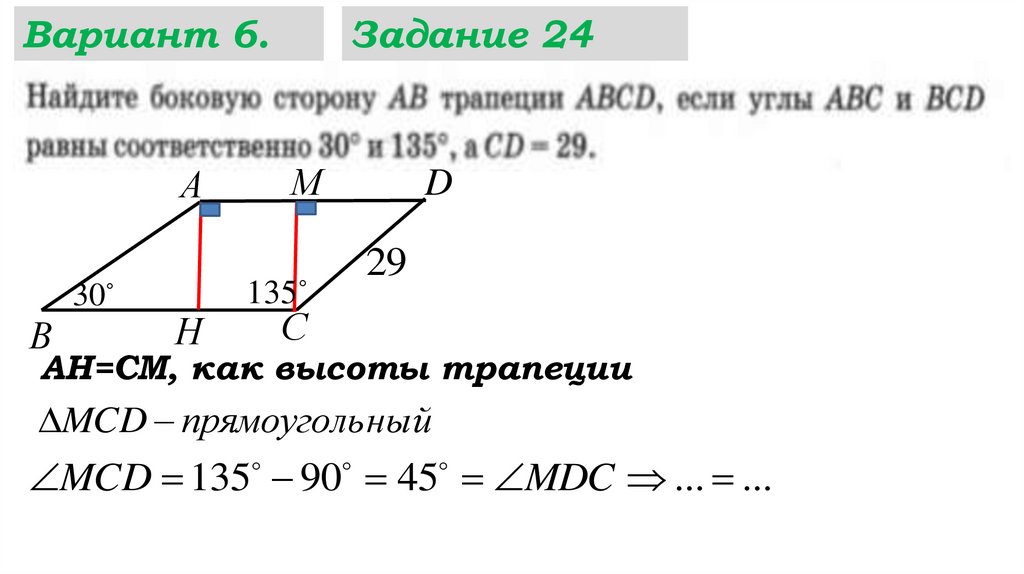
27.
Вариант 6.М
А
30
В
Н
Задание 24
135
D
29
С
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC ... ...
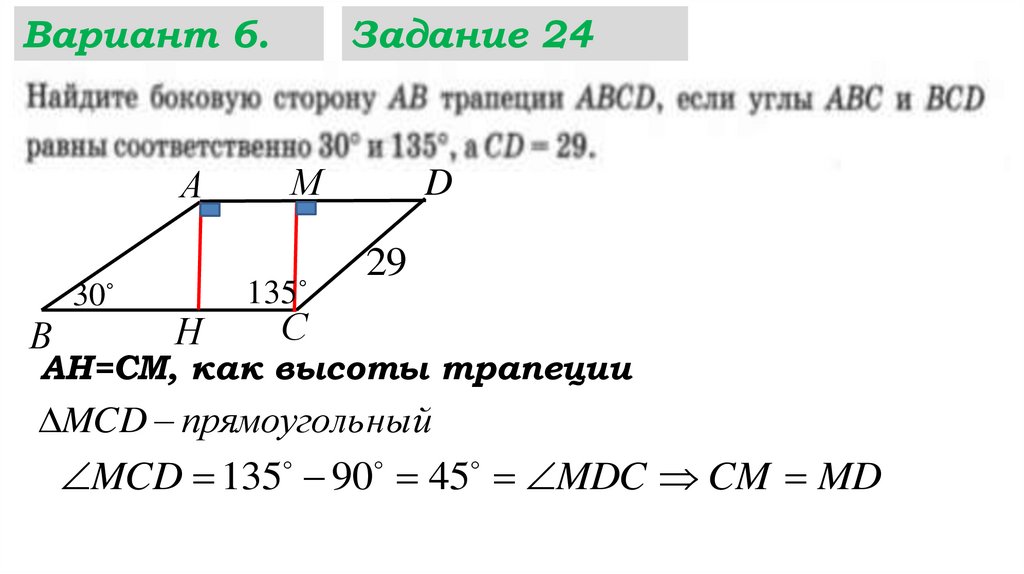
28.
Вариант 6.А
30
В
Н
Задание 24
М
135
D
29
С
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
29.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
С
По теореме Пифагора:
D
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
30.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
D
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
2
2
2
МС
MD
29
По теореме Пифагора:
31.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
АН=СМ, как высоты трапеции
D
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
По теореме Пифагора:
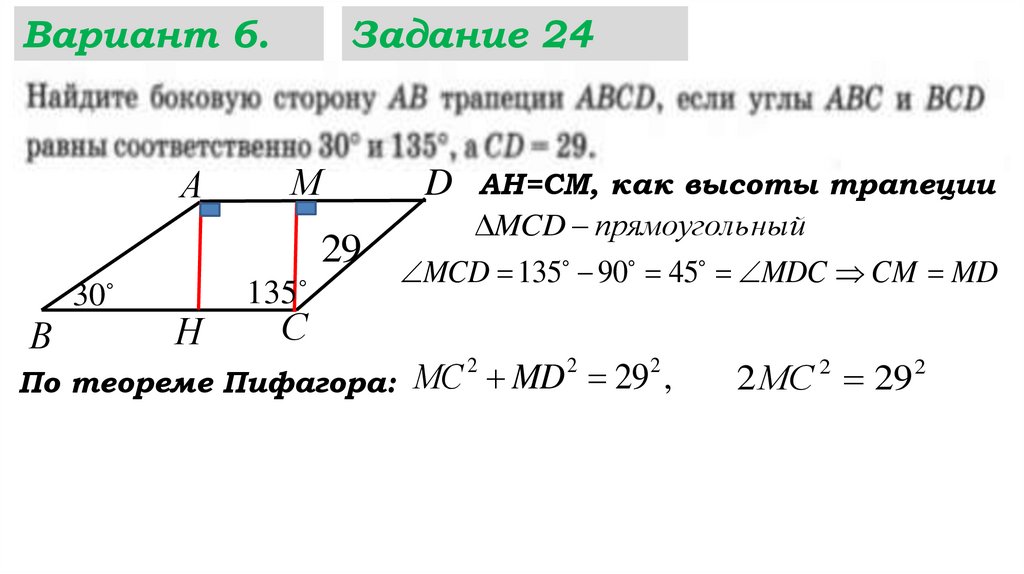
МС MD 29 ,
2
2
2
2 МС 29
2
2
32.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
1 2
МС 29
2
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
По теореме Пифагора:
2
АН=СМ, как высоты трапеции
D
МС
МС MD 29 ,
2
2
2
2 МС 29
2
2
33.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
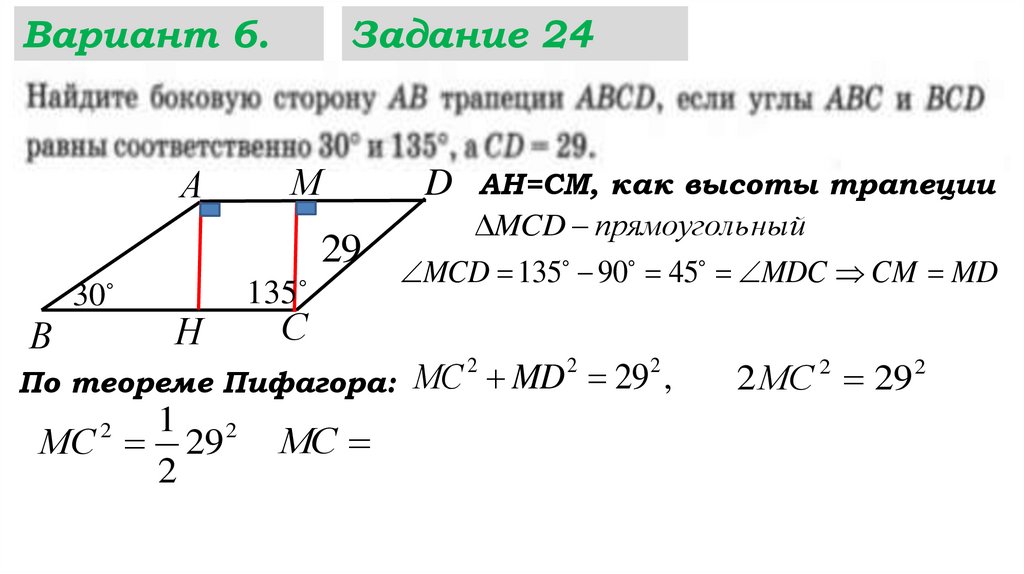
1 2
МС 29
2
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
МС MD 29 ,
29
МС
2
По теореме Пифагора:
2
АН=СМ, как высоты трапеции
D
2
2
2
2 МС 29
2
2
Какой треугольник теперь нужно рассмотреть?
34.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
АН=СМ, как высоты трапеции
D
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
МС MD 29 ,
2 МС 29
1 2
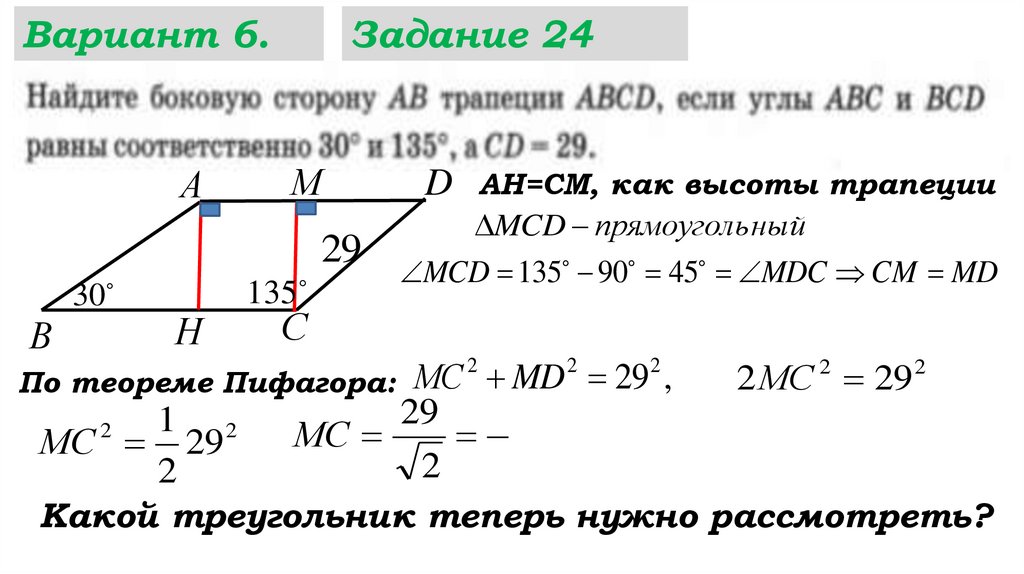
29 29 2
2
МС 29 МС
2
2
2
АВН прямоуголь ный с острым углом …
По теореме Пифагора:
2
2
2
2
2
35.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
1 2
МС 29
2
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
С
МС MD 29 ,
29 29 2
МС
2
2
По теореме Пифагора:
2
АН=СМ, как высоты трапеции
D
2
2
2
2 МС 29
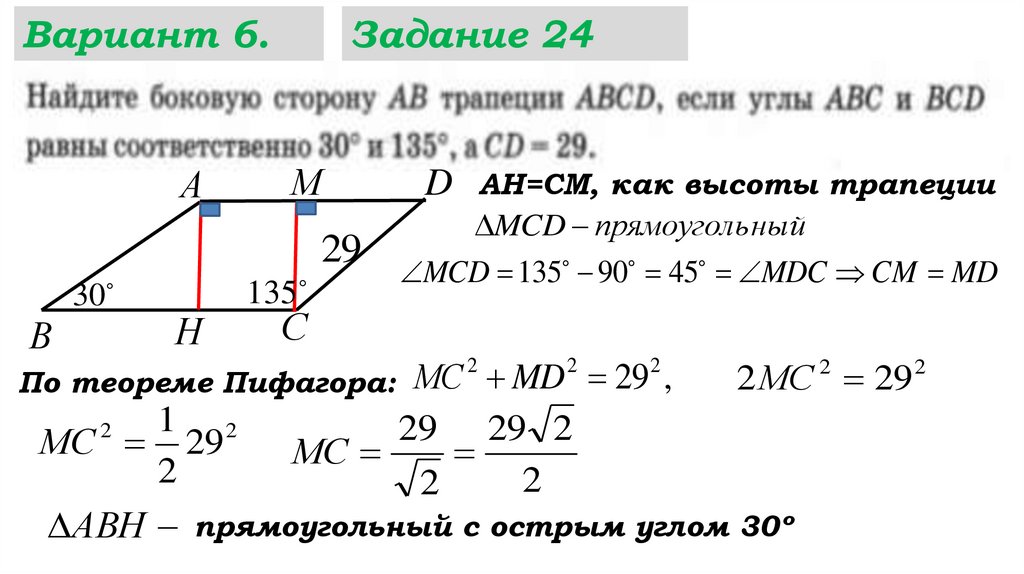
АВН прямоугольный с острым углом 30º
2
2
36.
Вариант 6.А
Задание 24
М
29
30
135
D
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
МС MD 29 ,
В
2
2
29
29
2
1
2
МС
29
2
2
МС 29 МС
2
2
2
АВН прямоуголь ный с острым углом 30º
Н
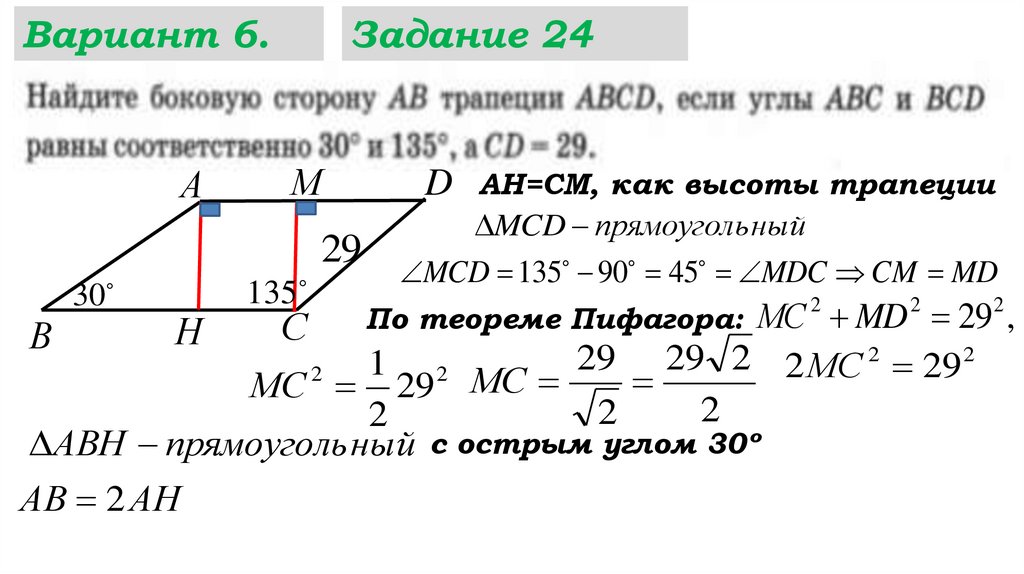
АВ 2 АН
С
По теореме Пифагора:
2
2
2
37.
Вариант 6.А
Задание 24
М
29
30
В
Н
135
С
D
АН=СМ, как высоты трапеции
MCD прямоуголь ный
MCD 135 90 45 MDC CM MD
По теореме Пифагора:
МС MD 29 ,
2
2
2 МС 29
2
2
29
29
2
1
2
2
МС
МС 29
2
2
2
АВН прямоуголь ный с острым углом 30º
АВ 2 АН
АВ 2 АН 29 2
Ответ : 29 2
2
38.
Вариант 6.Задание 25
Прочитайте задачу.
Выполните чертёж
39.
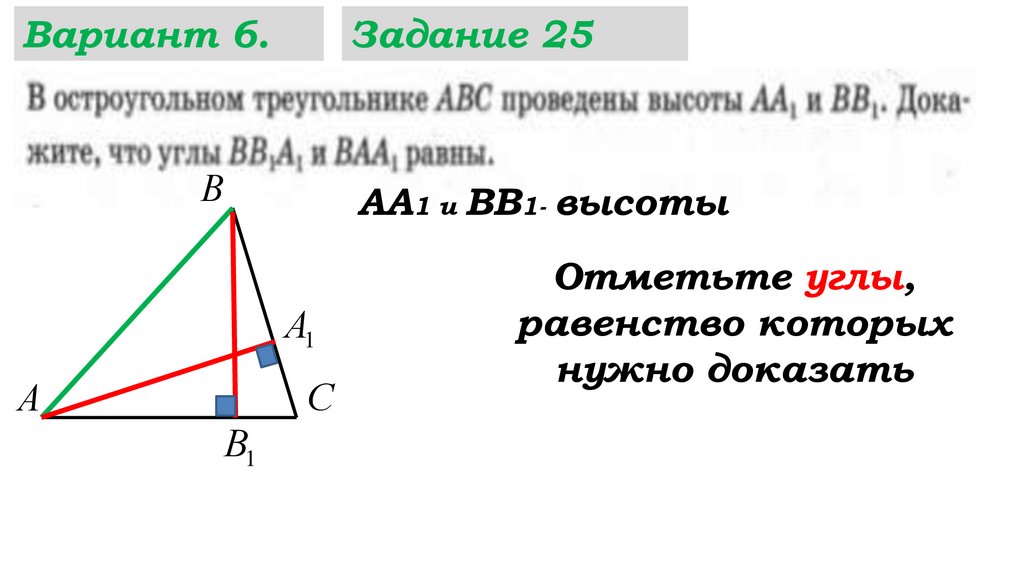
Вариант 6.Задание 25
В
АА1 и ВВ1- высоты
А1
С
А
В1
Отметьте углы,
равенство которых
нужно доказать
40.
Вариант 6.Задание 25
В
АА1 и ВВ1- высоты
А1
С
А
В1
Назовите прямые углы,
опирающиеся на одну
сторону треугольника
На какой фигуре будут
лежать точки АВА1В1
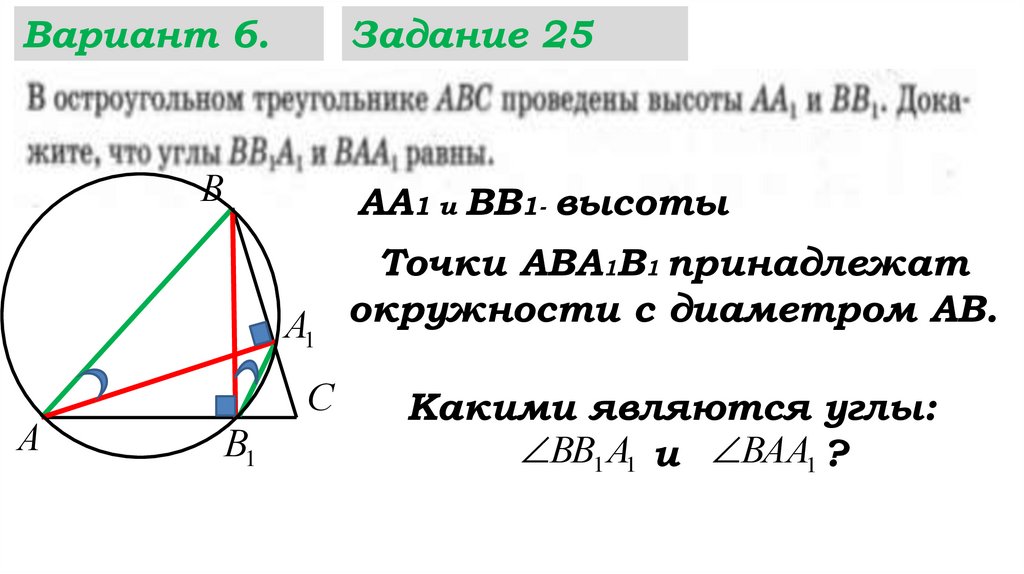
41.
Вариант 6.Задание 25
В
АА1 и ВВ1- высоты
Точки АВА1В1 принадлежат
окружности
с
диаметром
АВ.
А1
А
С
В1
Какими являются углы:
ВВ1 А1 и ВАА1 ?
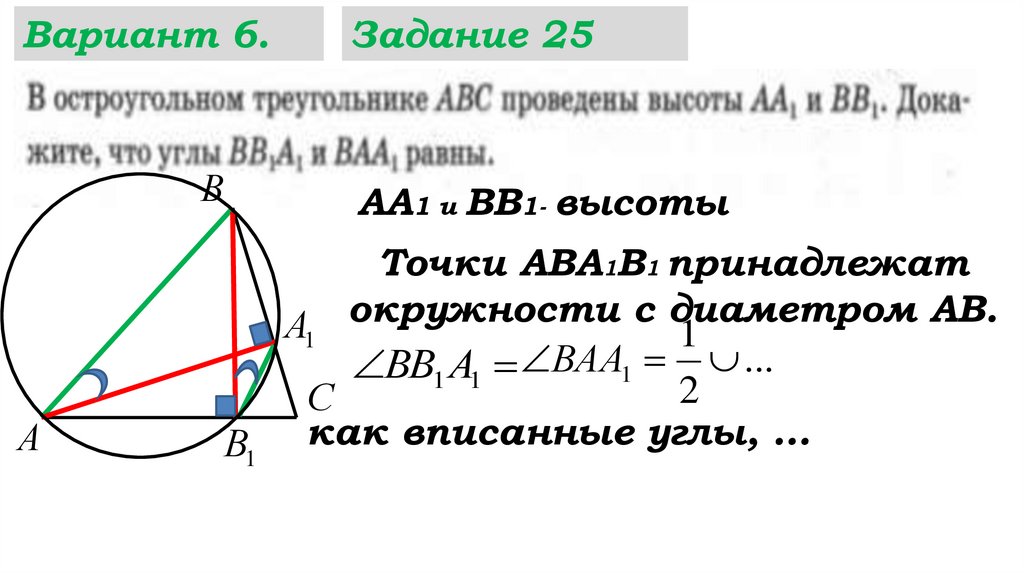
42.
Вариант 6.В
А
Задание 25
АА1 и ВВ1- высоты
Точки АВА1В1 принадлежат
окружности
с
диаметром
АВ.
А1
1
ВВ1 А1 ВАА1 ...
2
С
В1 как вписанные углы, …
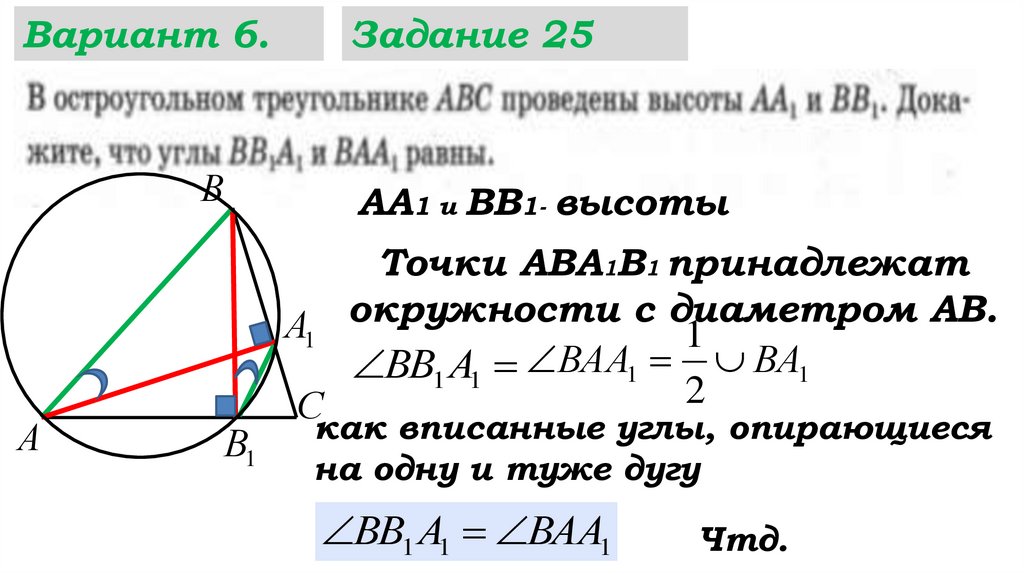
43.
Вариант 6.В
А
Задание 25
АА1 и ВВ1- высоты
В1
Точки АВА1В1 принадлежат
окружности
с
диаметром
АВ.
А1
1
ВВ1 А1 ВАА1 ВА1
2
С
как вписанные углы, опирающиеся
на одну и туже дугу
ВВ1 А1 ВАА1
Чтд.
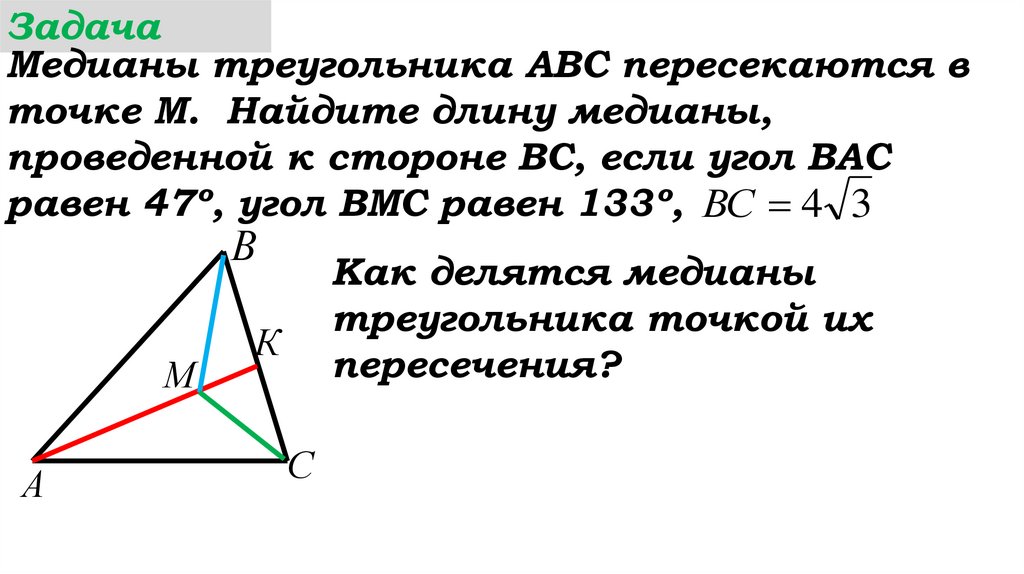
44.
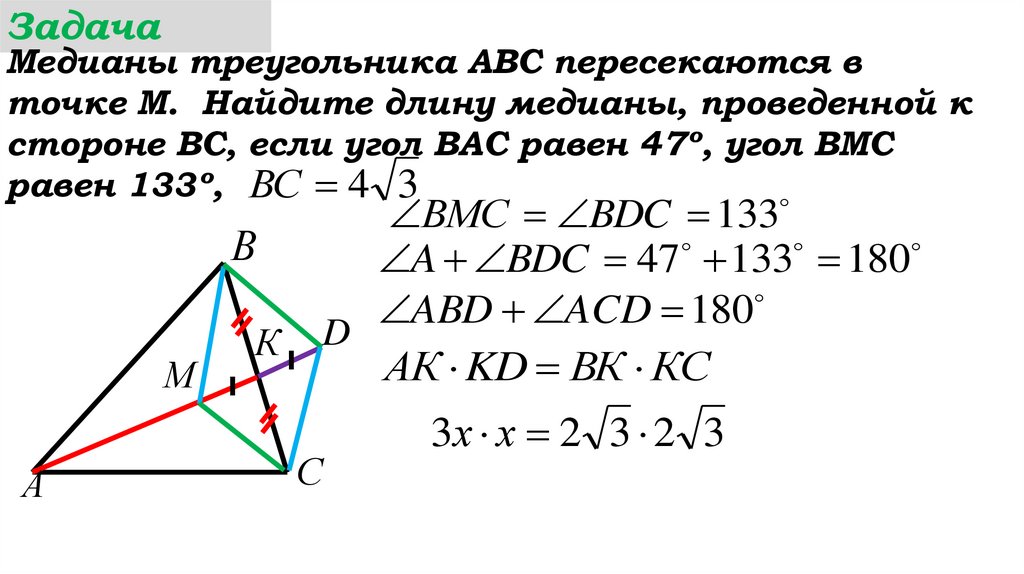
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
Прочитайте задачу.
Выполните чертеж
45.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
В
М
А
Как делятся медианы
треугольника точкой их
пересечения?
К
С
46.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
В
М
А
Медианы треугольника
точкой пересечения делятся
К
в отношении 2:1, считая от
вершины.
АМ : МК=… : …
С
47.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
В
М
А
D
К
С
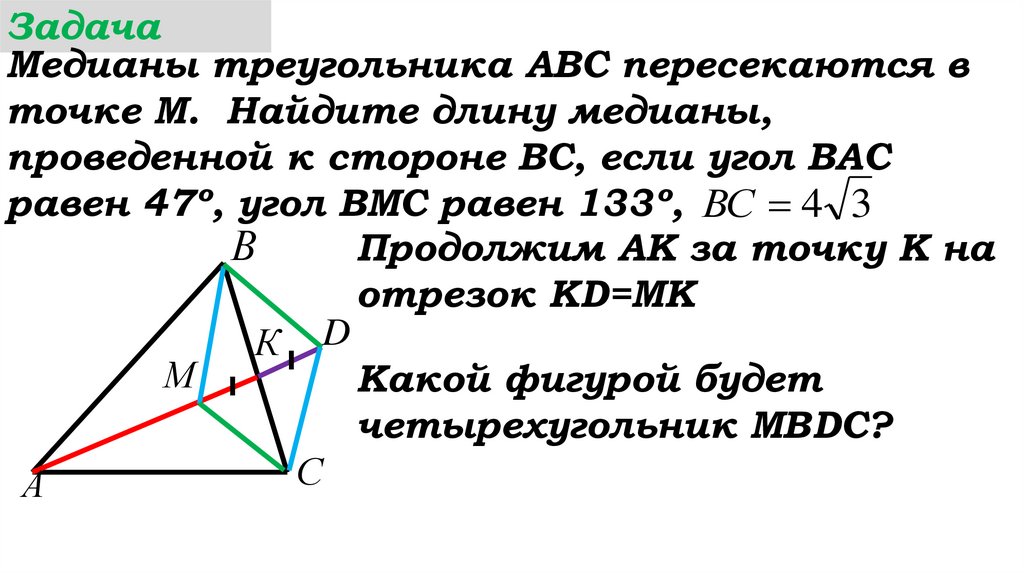
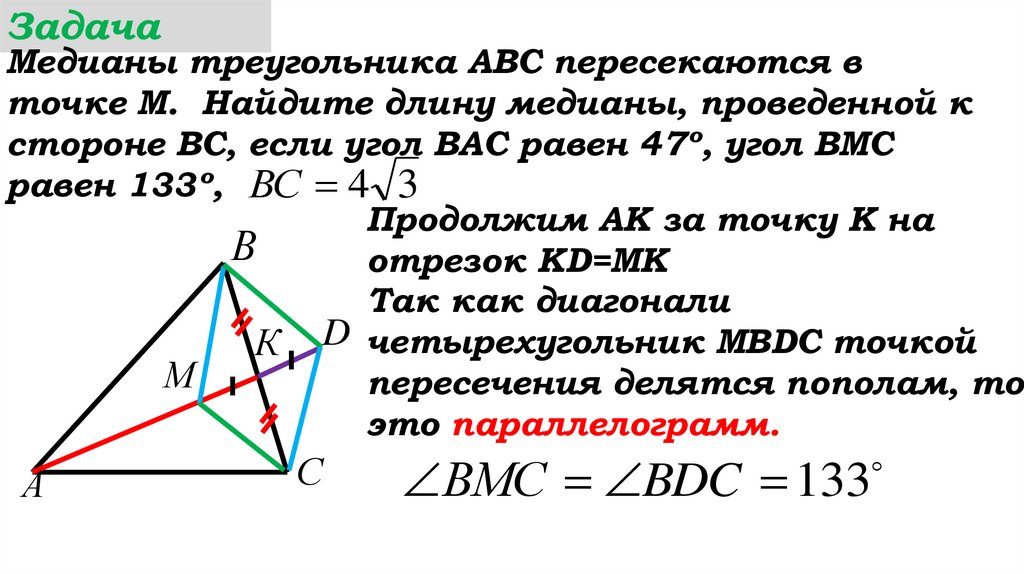
Продолжим АК за точку К на
отрезок КD=MK
48.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
В
Продолжим АК за точку К на
отрезок КD=MK
К D
М
Какой фигурой будет
четырехугольник МВDC?
С
А
49.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы,
проведенной к стороне ВС, если угол ВАС
равен 47º, угол ВМС равен 133º, ВС 4 3
В
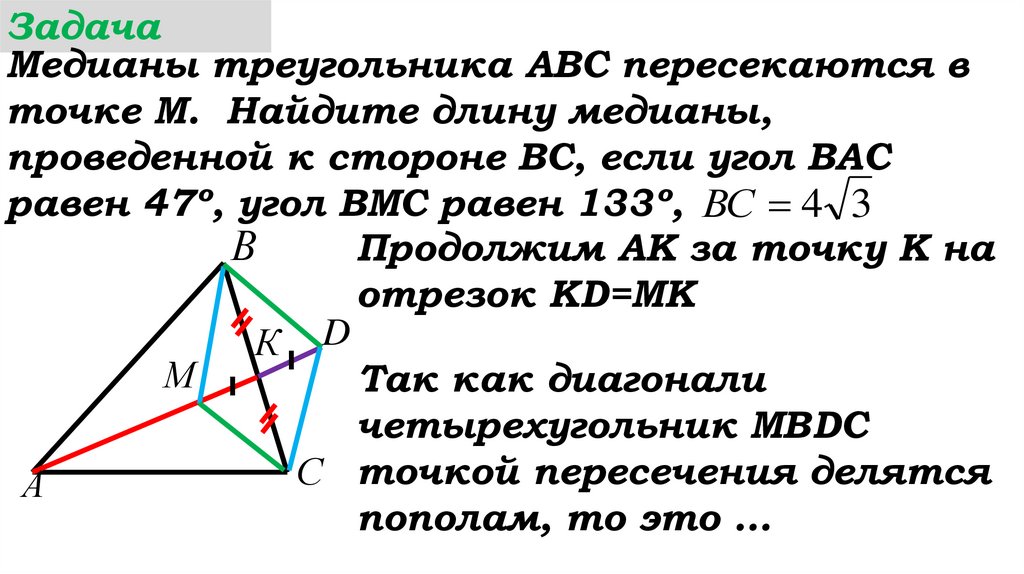
Продолжим АК за точку К на
отрезок КD=MK
К D
М
Так как диагонали
четырехугольник МВDC
С точкой пересечения делятся
А
пополам, то это …
50.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
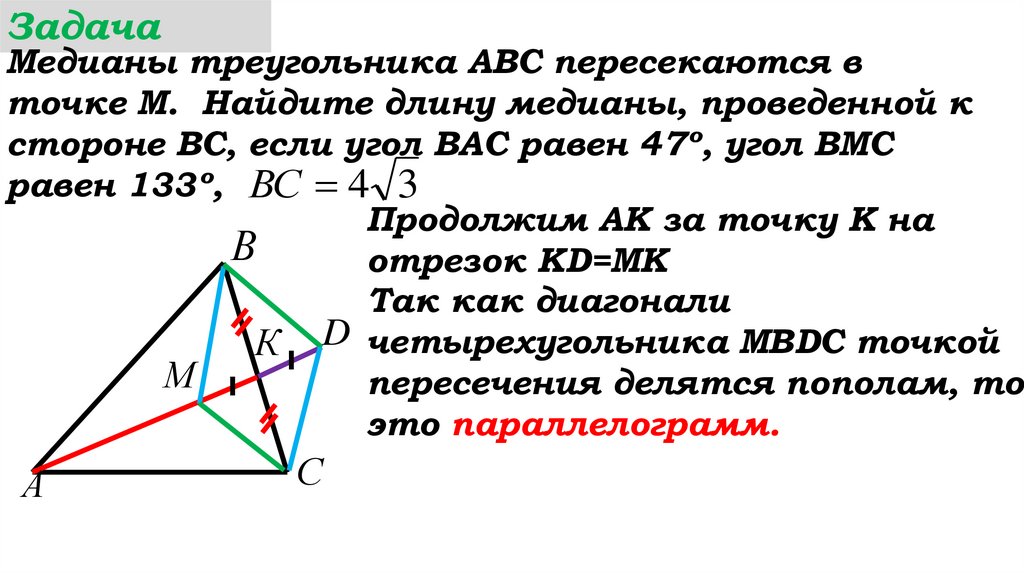
Продолжим АК за точку К на
В
отрезок КD=MK
Так как диагонали
К D четырехугольника МВDC точкой
М
пересечения делятся пополам, то
это параллелограмм.
А
С
51.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
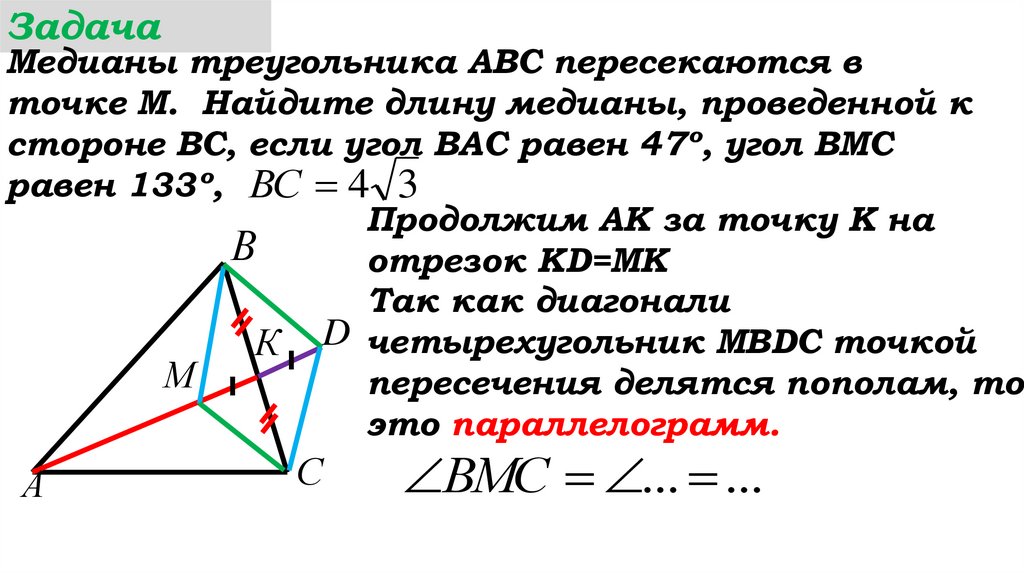
Продолжим АК за точку К на
В
отрезок КD=MK
Так как диагонали
К D четырехугольник МВDC точкой
М
пересечения делятся пополам, то
это параллелограмм.
А
С
ВMС ... ...
52.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
Продолжим АК за точку К на
В
отрезок КD=MK
Так как диагонали
К D четырехугольник МВDC точкой
М
пересечения делятся пополам, то
это параллелограмм.
А
С
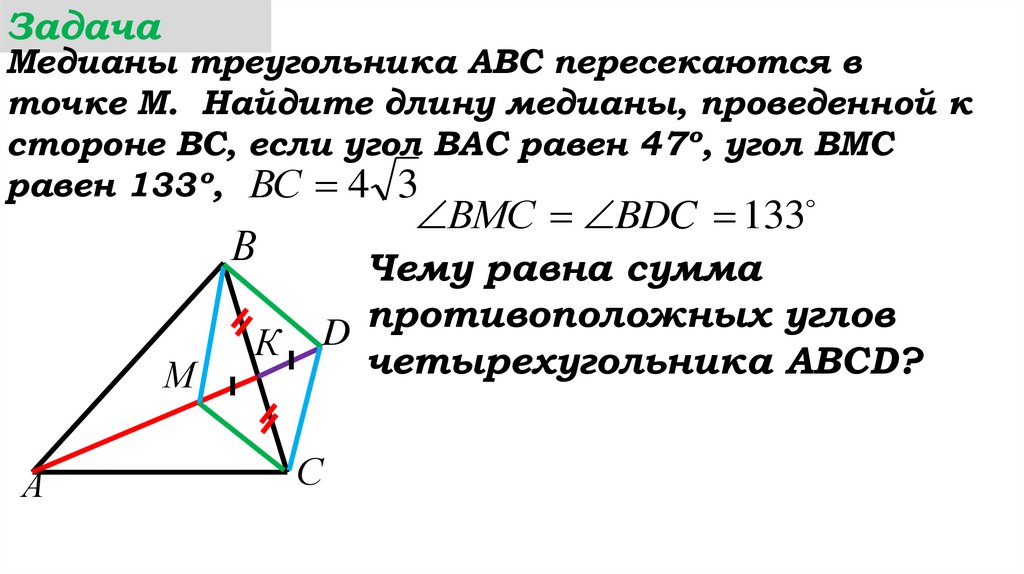
ВMС BDC 133
53.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
ВMС BDC 133
Чему равна сумма
противоположных
углов
D
четырехугольника ABCD?
С
54.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
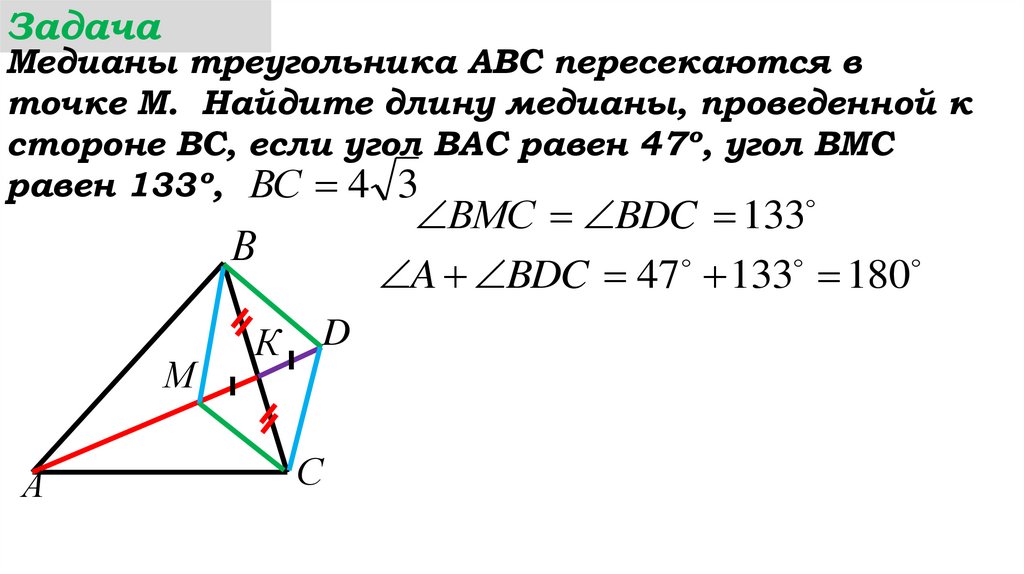
ВMС BDC 133
В
A BDC ...
М
А
К
D
С
55.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
ВMС BDC 133
A BDC 47 133 180
В
М
А
К
D
С
56.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
ВMС BDC 133
A BDC 47 133 180
В
М
А
К
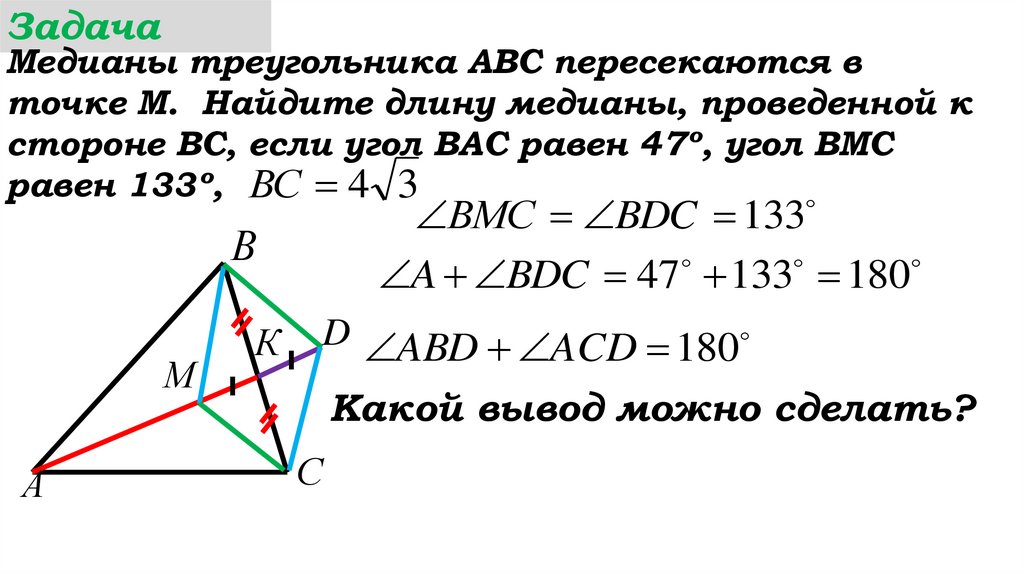
D ABD ACD 180
Какой вывод можно сделать?
С
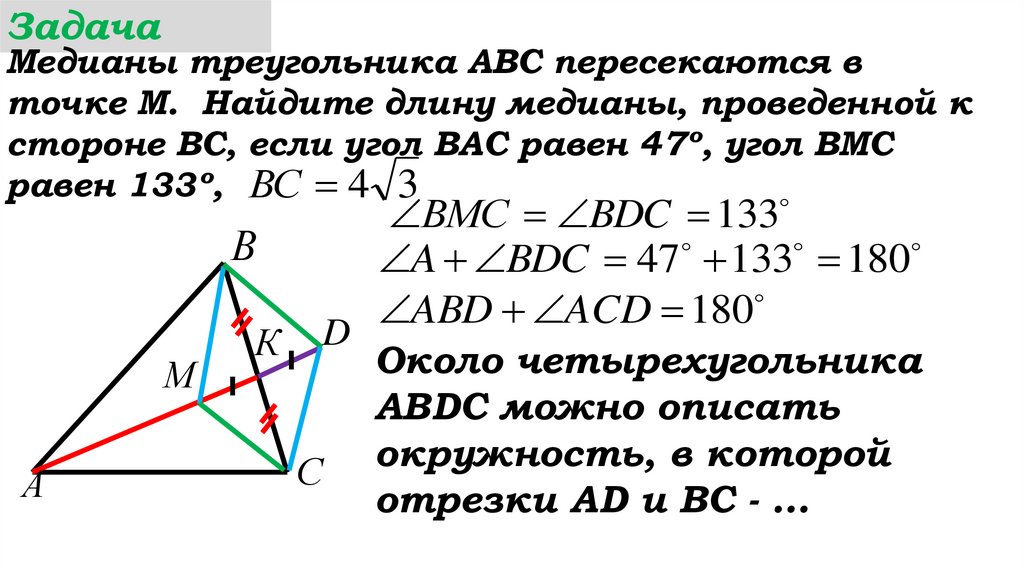
57.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
D
С
ВMС BDC 133
A BDC 47 133 180
ABD ACD 180
Около четырехугольника
ABDC можно описать
окружность, в которой
отрезки AD и ВС - …
58.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
D
С
ВMС BDC 133
A BDC 47 133 180
ABD ACD 180
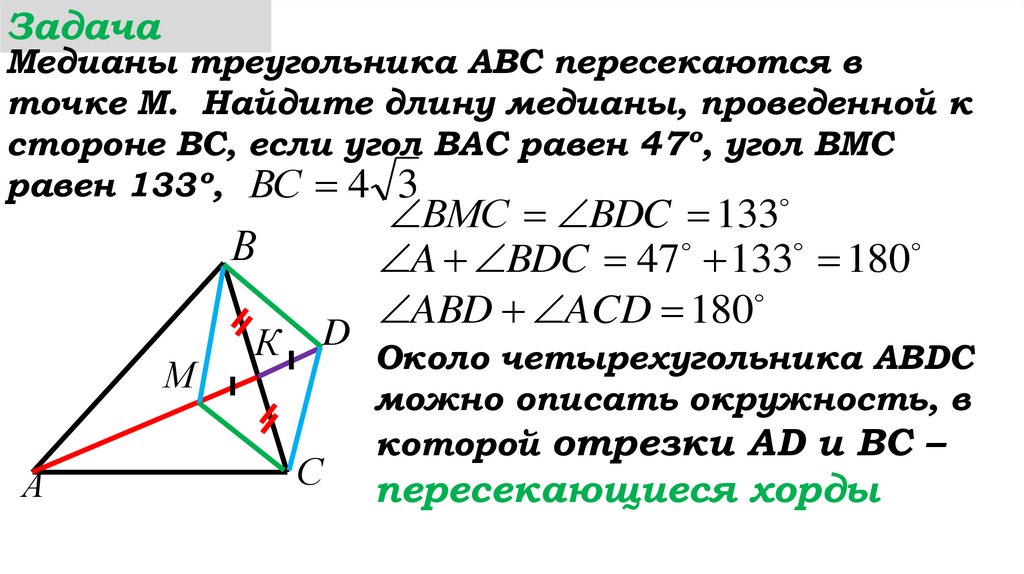
Около четырехугольника ABDC
можно описать окружность, в
которой отрезки AD и ВС –
пересекающиеся хорды
59.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
D
С
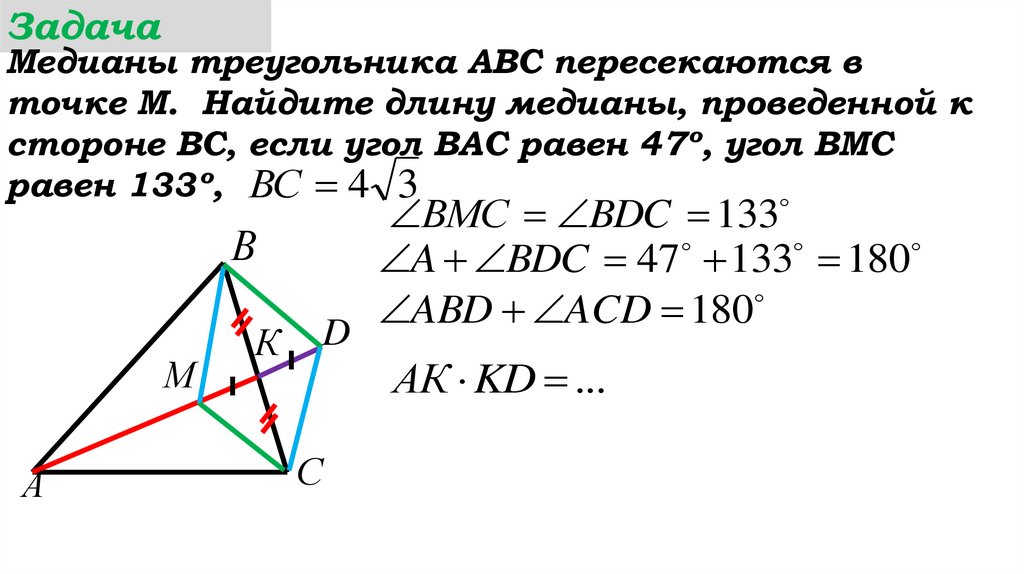
ВMС BDC 133
A BDC 47 133 180
ABD ACD 180
АК KD ...
60.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
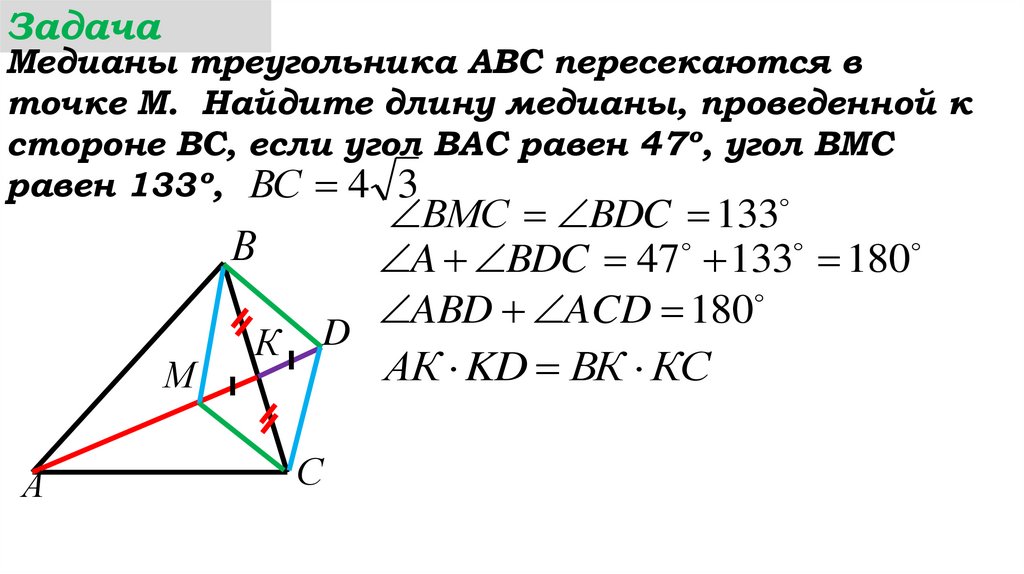
ВMС BDC 133
A BDC 47 133 180
ABD ACD 180
D
АК KD ВК КС
С
61.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
В
М
А
К
ВMС BDC 133
A BDC 47 133 180
ABD ACD 180
D
АК KD ВК КС
С
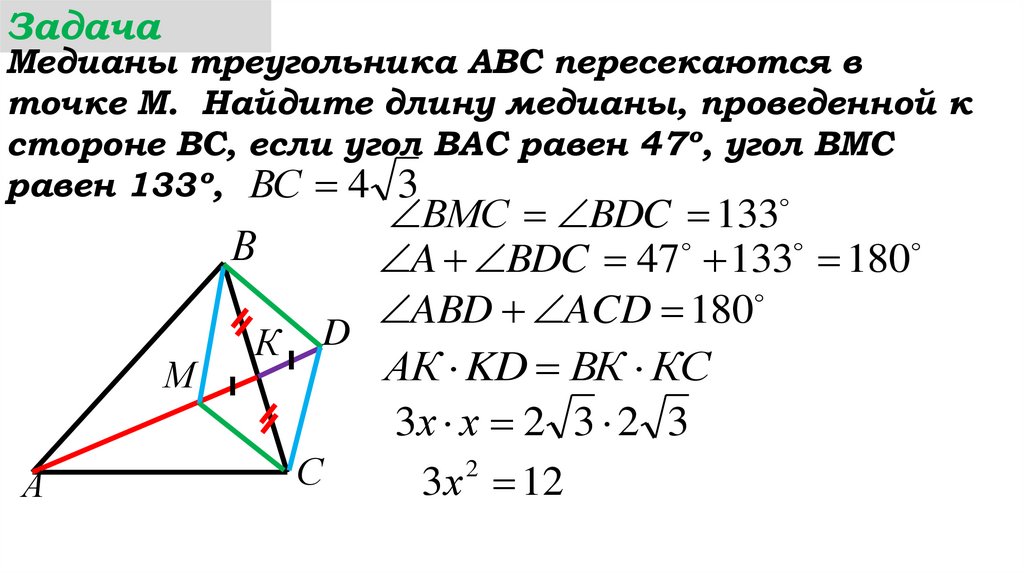
3х х 2 3 2 3
62.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
А
ВMС BDC 133
В
A BDC 47 133 180
ABD ACD 180
К D
АК KD ВК КС
М
3х х 2 3 2 3
2
С
3х 12
63.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
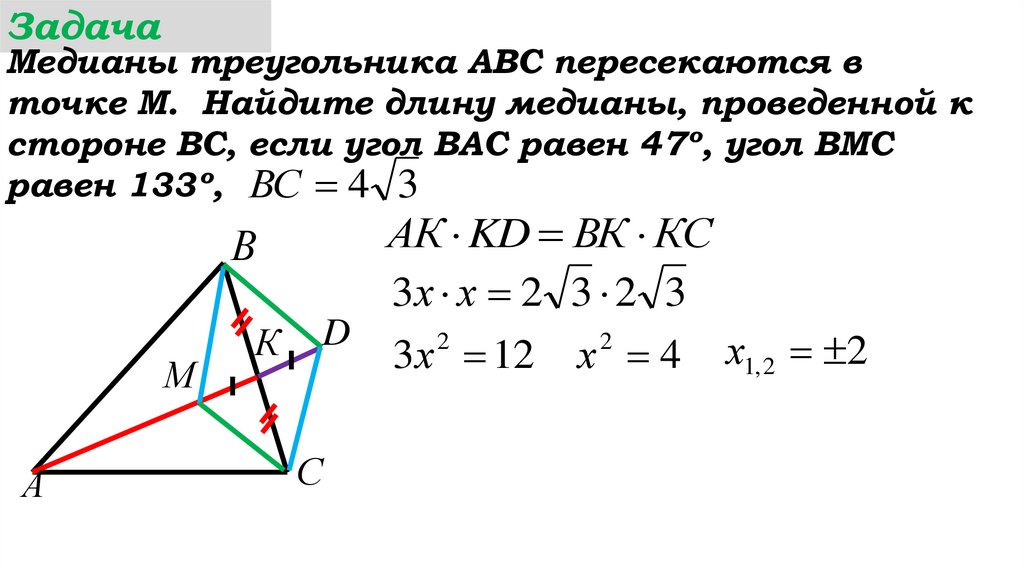
АК KD ВК КС
3х х 2 3 2 3
К D 3х 2 12 х 2 4 х1, 2 2
В
М
А
С
64.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
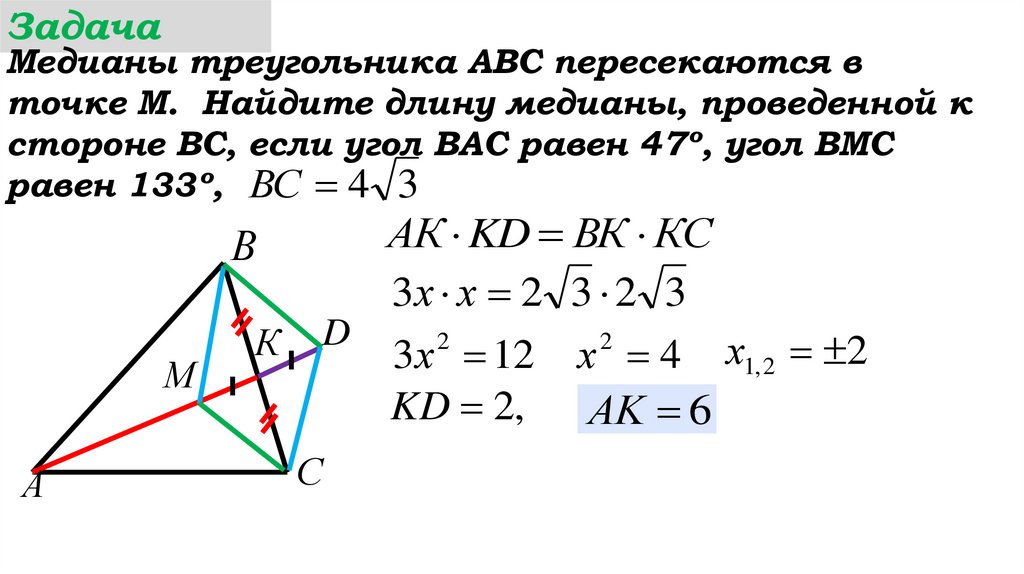
АК KD ВК КС
3х х 2 3 2 3
К D 3х 2 12 х 2 4 х1, 2 2
KD 2, АK ...
В
М
А
С
65.
ЗадачаМедианы треугольника АВС пересекаются в
точке М. Найдите длину медианы, проведенной к
стороне ВС, если угол ВАС равен 47º, угол ВМС
равен 133º, ВС 4 3
АК KD ВК КС
3х х 2 3 2 3
К D 3х 2 12 х 2 4 х1, 2 2
KD 2,
АK 6
В
М
А
С
66.
Вариант 1.Задание 26
67.
Вариант 6.Задание 26























 mathematics
mathematics








