Similar presentations:
Тригонометрические функции. Формулы двойного угла
1. Раздел программы «Тригонометрические функции».
Тема урока«Формулы двойного угла »
2. «Величие человека –в его способности мыслить» Блез Паскаль. Цели урока :
• Образовательные : формирование предметныхкомпетенций( вывод формул двойного угла)на
основе ранее изученных компетенций: формул
сложения тригонометрических функций.
• Развивающие :развивать практические навыки
применения формул двойного угла при
решении примеров.
• Воспитательные :Воспитывать
коммуникативные компетенции через
применение на уроке различных форм
взаимодействия :индивидуальной , групповой ,
коллективной.
3. Исходя из целей урока , предлагается следующий порядок работы на уроке:
• Математический диктант- проверка домашнегозадания.
• Повторение понятий – формулы сложения и
основные тригонометрические тождества.
• Вывод формул двойного угла.
• Рассмотрение примеров на применение
полученных знаний.
• Проверка начальных умений и навыков.
• Итог урока.
4. Формулы сложения.
sin sin cos cos sincos( ) cos cos sin sin
tg tg
tg
1 tg tg
5. Можно ли применить записанные формулы для решения следующих примеров ?
sincos( )
tg
6.
sin sin cos cos sin 2 sin coscos( ) cos cos sin sin cos 2 sin 2
tg tg
2tg
tg
1 tg tg 1 tg 2
7. Полученные формулы, формулы двойного угла.
2asin 2a 2 sin cos
cos 2a cos sin
2tg
tg 2a
2
1 tg
2
2
8. Задание1.
Найти значение sin2a , зная чтоcos a=-0,8
и a -угол 3 четверти.
Алгоритм решения:
1.
Записать основное тригонометрическое тождество.
2.
Выразить нужную функцию.
3.
Определить какая четверть и знак функции в этой
четверти.
4.
Извлечь корень
5.
все величины подставить в формулу.
9. Решение:
sin 2 2 sin cossin 1 cos 1 0,8 1 0,64 0,36
2
2
2
sin 0,36 0,6
a 3четверти, знак "-"
sin -0,6
sin 2a 2 0,6 0,8 0,96
10. Задание 2. Вычисли , используя формулу двойного угла:
2 sin8
cos
8
.
Решение : 2 sin a cos a sin 2a
2 sin
8
cos
8
sin 2
8
sin
4
2
2
11. Задание 3. Упрости, используя формулу двойного угла:
sin 100 0.
0
cos 50
Решение :
0
sin 100
cos 500
0
0
2
sin
50
cos
50
sin 2 50
0
2 sin 50 .
0
0
cos 50
cos 50
0
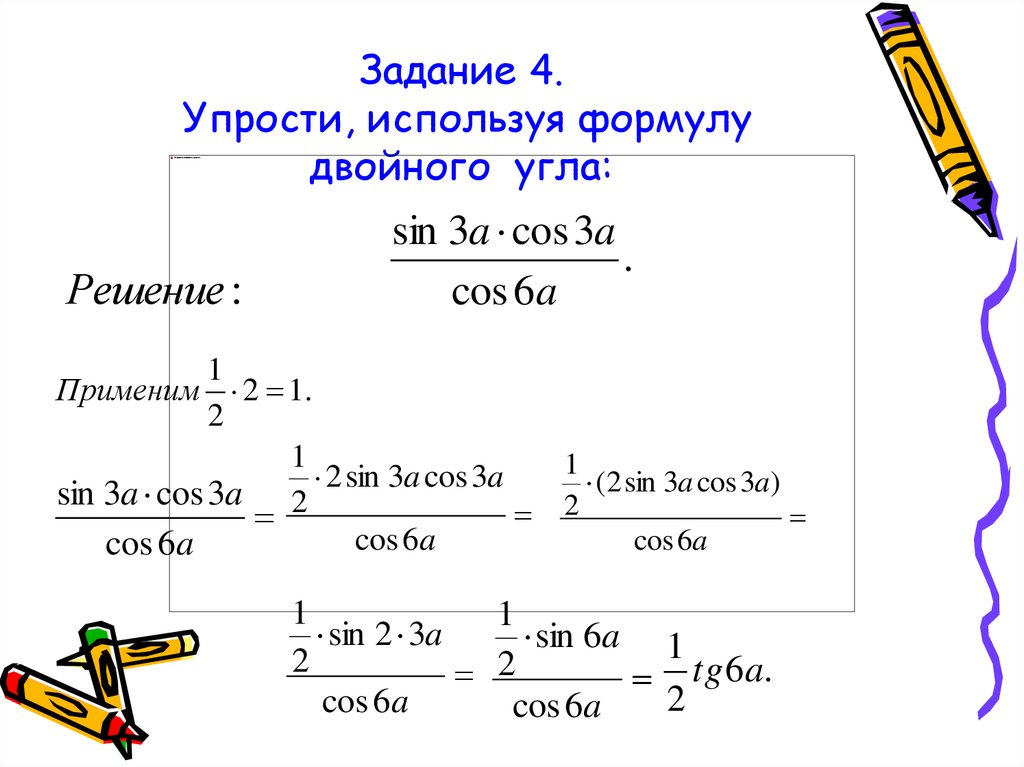
12. Задание 4. Упрости, используя формулу двойного угла:
Решение :sin 3a cos 3a
.
cos 6a
1
Применим 2 1.
2
1
1
2 sin 3a cos 3a
(2 sin 3a cos 3a)
sin 3a cos 3a 2
2
cos 6a
cos 6a
cos 6a
1
1
sin 2 3a
sin 6a 1
2
2
tg 6a.
2
cos 6a
cos 6a
13. Задание 5. Упрости, используя формулу двойного угла:
cos 2 cos 2 .Решение :
2
2
2
cos
cos
a
sin
a
cos cos 2
2
cos cos a sin a sin 2 a.
2
2
2
14. Упрости:
01.2 sin 75 cos 75
0
2. cos 75 sin 75
2
3. cos
2
0
sin
2
2
0
8
8
0
0
4. sin 15 cos 15
2
2
5. cos
sin
8
8
2
15. Работа в группах.(1 уровень )
1 вариант.а) sin 2a
2 вариант.
2
а) 2 cos
sin 2
sin a
б)
в)
cos 2 sin 2 a
2 cos 2 30 0
sin 60 0
б)
sin 2 cos 2
в)
sin 60 0
sin 30 0
16. Работа в группах.(1 уровень )
1 вариант.а) sin 2a 2 sin cos
sin a
б)
sin a
2 cos
cos 2 sin 2 a cos 2 sin 2
2 вариант.
2
2
а) 2 cos 2 cos
sin 2
б)
cos
ctg
sin
sin 2 cos 2 sin 2 cos 2 a
sin 2 cos 2
sin 2 cos 2
2
0
2
0
2
0
в) 2 cos 300 2 cos 300 2 cos0 30 0
sin 60
sin 2 30
2 sin 30 cos 30
0
cos 30
ctg300 3.
0
sin 30
2 sin cos
в)
sin 600 sin 2 300 2 sin 30 0 cos 30 0
sin 30 0
sin 30 0
sin 30 0
3
2 cos 30 0 2
3
2
17. Работа в группах.(2 уровень )
1 вариант.2 вариант.
Докажите формулу ,используя основное
тригонометрическое тождество:
cos 2 1 2 sin 2
cos 2 2 cos 2 1
18.
1 вариант.Используем основное тригонометрическое тождество.
2
2
Сделаем замену cos 1 sin .
cos 2 cos 2 sin 2 1 sin 2 sin 2 1 2 sin 2
2 вариант.
Используем основное тригонометрическое тождество.
2
2
Сделаем замену sin 1 cos a.
cos 2 cos 2 sin 2 cos 2 1 cos 2 cos 2 1
cos 2 2 cos 2 1
19. Домашнее задание:
1.Вучить формулыдвойного угла.
2.Упрости :
a ) sin cos
12
12
б )1 2соs
2
12
.
2


















 mathematics
mathematics








