Статистическая обработка данных в механике. Комбинаторика, теория вероятности

1.

Применение
статистической
обработки данных
в механике
Комбинаторика, теории
верояности
Выполнял Фомин Илья

2.

Статистическая обработка
Статистическая обработка.
применение аппарата биомертии
(прикладной статистики) для
выявления каких-либо свойств или
закономерностей
связи данных объектов. Основные
моменты статистической обработки
- формирование случайной выборки
и выбор критерия сравнения или
расчета.

3.

комбинаторика
В науке и на практике очень часто встречается задачи, решения которые
приходится составлять комбинанации из конечного числа элементов, а затем
подсчитывать числа этих комбинаций.
Такие задачи называют комбинаторными задачами.
Раздел математики, в котором рассматриваются подобные задачи, называют
комбинаторикой.
Комбинаторика (от лат. combinare – соединять, сочетать) –это раздел математики,
в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных
тем или иным условиям, можно составить из заданных объектов.

4.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
К
Г
М

5.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
ЛК, ЛГ, ЛМ
К
Г
М

6.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
ЛК, ЛГ, ЛМ
КГ, КМ
К
Г
М

7.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
ЛК, ЛГ, ЛМ
КГ, КМ
ГМ
К
Г
М

8.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
ЛК, ЛГ, ЛМ
КГ, КМ
ГМ
Ответ:6 партий.
К
Г
М

9.

Лера, Карина, Глеб и Максим решили сыграть друг с
другом по одной партии в шахматы. Сколько партий
было сыграно?
Л
ЛК, ЛГ, ЛМ
КГ, КМ
ГМ
Ответ:6 партий.
К
Г
М
Способ рассуждений,
Которым мы
воспользовались при
решении задачи,
называется перебором
возможных
вариантов

10.

Определить, сколько различных трёхзначных чисел
можно составить, используя цифры 2, 6, 8 и 9
(цифры в числе не должны повторяться).

11.

Определить, сколько различных трёхзначных чисел
можно составить, используя цифры 2, 6, 8 и 9
(цифры в числе не должны повторяться).
1
цифра:
2
6
8
9

12.

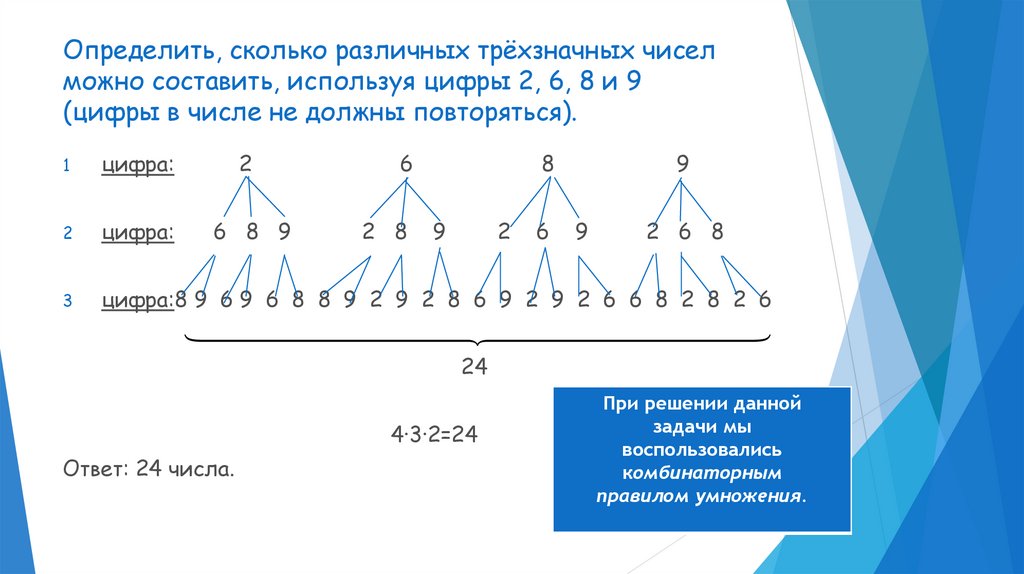
Определить, сколько различных трёхзначных чисел
можно составить, используя цифры 2, 6, 8 и 9
(цифры в числе не должны повторяться).
1
цифра:
2
2
цифра:
3
цифра:8 9 6 9 6 8 8 9 2 9 2 8 6 9 2 9 2 6 6 8 2 8 2 6
6 8 9
6
2 8
8
9
2
6
9
9
2 6 8
24
4∙3∙2=24
Ответ: 24 числа.
При решении данной
задачи мы
воспользовались
комбинаторным
правилом умножения.

13.

Комбинаторика
В комбинаторике различают 3 вида различных
комбинаций элементов конечного множества:
перестановки;
размещения;
сочетания.