Similar presentations:
Центральная симметрия
1.
2.
«Симметрия» - слово греческого происхождения. Оно означаетсоразмерность, наличие определенного порядка, закономерности в
расположении частей
Виды симметрии:
Центральная
симметрия
Осевая
симметрия
3.
Фигура называется симметричной относительноточки
O,
если
для
каждой
точки
фигуры
симметричная ей точка относительно точки O
также
принадлежит
этой
фигуре.
Точка
O
называется центром симметрии.
4.
Точки А и А1 называются симметричнымиотносительно точки О, если О середина отрезка АА1
.
.
М
.
А
.
О
.
N
.
.
А1
М1
N1
N
симметрична N1, т.к. NО = ОN1
М не симметрична М1, т.к. МО ≠ ОМ1
О симметрична сама себе
5. Алгоритм построения
Отметим на листе бумагипроизвольные точки O и A.
Проведём через точки прямую
OA.
А1
О
А
На этой прямой
отложим от точки O
отрезок OA1, равный
отрезку AO, но по
другую сторону от
точки O.
Точка А симметрична точке А1 относительно точки О.
О - центр симметрии.
6.
Точки А и А1 называются симметричными относительноточки О, если О – середина отрезка АА1
А1
Образ точки А
О
А
АО = ОА1
Точка О – центр симметрии
Прообраз
точки А1
7. Фигуры , симметричные относительно точки (примеры)
8.
Центром симметрииокружности является центр
окружности.
О
О
Центр симметрии
параллелограмма – точка
пересечения его диагоналей
9.
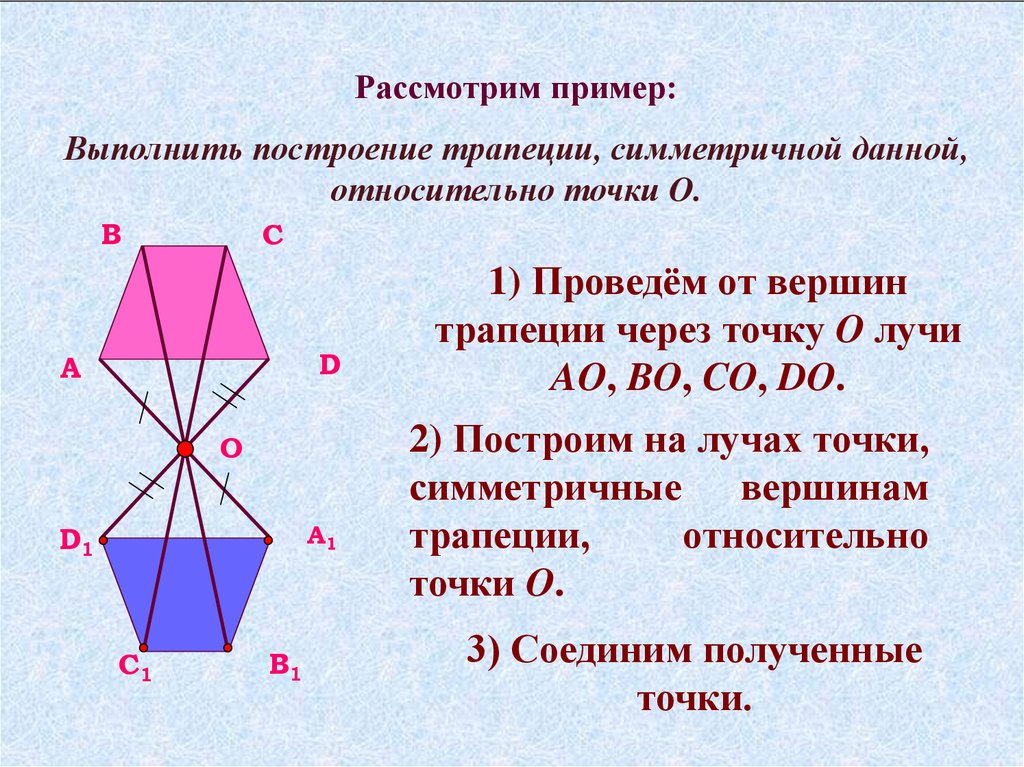
Рассмотрим пример:Выполнить построение трапеции, симметричной данной,
относительно точки O.
B
C
D
A
O
A1
D1
C1
B1
1) Проведём от вершин
трапеции через точку O лучи
AO, BO, CO, DO.
2) Построим на лучах точки,
симметричные вершинам
трапеции,
относительно
точки O.
3) Соединим полученные
точки.
10.
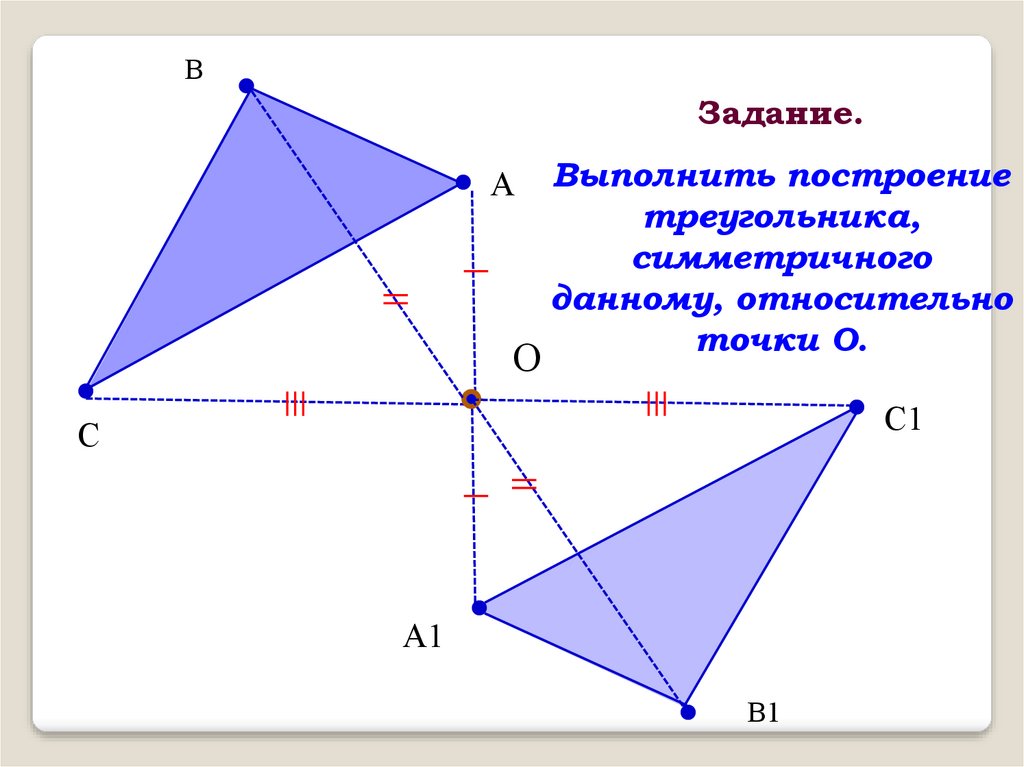
ВЗадание.
А
О
Выполнить построение
треугольника,
симметричного
данному, относительно
точки O.
С1
С
А1
В1
11.
Ответьте на вопрос:•обладает ли центральной
симметрией прямая?
У прямой бесконечное множество центров
симметрии (любая точка прямой является
ее центром симметрии)
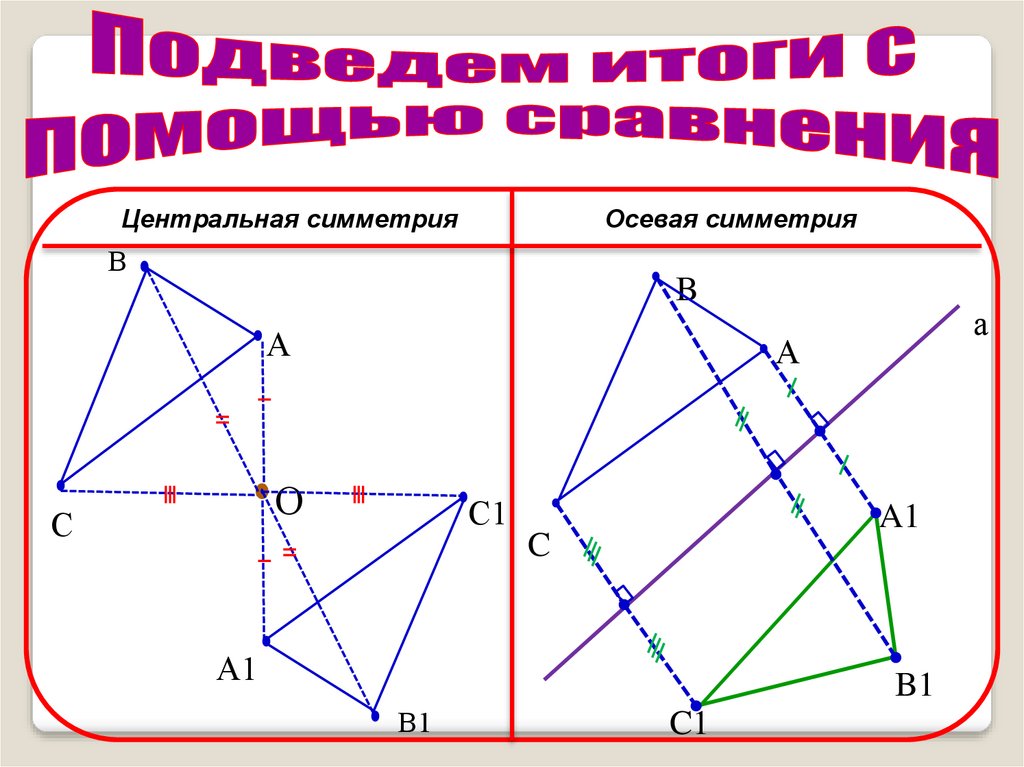
12.
Центральная симметрияОсевая симметрия
В
B
А
А
О
С
а
С1
A1
C
А1
B1
В1
C1
13.
В классе № 694, 699, 700, 704,705, 708, 709, 715, 717, 718
ДОМАШНЕЕ ЗАДАНИЕ
Изучить § 19, вопросы 1-6,
Б-№ 695, 696, 706, 707, 710,
П-716
13










 mathematics
mathematics








