Similar presentations:
Элементы теории трения, расчет и технология применения фрикционно-подвижных соединений
1.
ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ,РАСЧЕТ И ТЕХНОЛОГИЯ ПРИМЕНЕНИЯ
ФРИКЦИОННО-ПОДВИЖНЫХ СОЕДИНЕНИЙ
УЗДИН А.М., ЕЛИСЕЕВ О.Н., , НИКИТИН А.А., ПАВЛОВ В.Е., СИМКИН А.Ю.,
КУЗНЕЦОВА И.О.
ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ,
РАСЧЕТ И ТЕХНОЛОГИЯ ПРИМЕНЕНИЯ
ФРИКЦИОННО-ПОДВИЖНЫХ СОЕДИНЕНИЙ
2.
2СОДЕРЖАНИЕ
1
Введение
3
2
Элементы теории трения и износа
6
3
Методика расчета одноболтовых ФПС
18
3.1
Исходные посылки для разработки методики расчета ФПС
18
3.2
Общее уравнение для определения несущей способности ФПС.
20
3.3
Решение общего уравнения для стыковых ФПС
21
3.4
Решение общего уравнения для нахлесточных ФПС
22
4
Анализ экспериментальных исследований работы ФПС
26
5
Оценка
параметров
диаграммы
деформирования
многоболтовых
фрикционно-подвижных соединений (ФПС)
31
5.1
Общие положения методики расчета многоболтовых ФПС
31
5.2
Построение уравнений деформирования стыковых многоболтовых ФПС
32
5.3
Построение уравнений деформирования нахлесточных многоболтовых 38
ФПС
6
Рекомендации по технологии изготовления ФПС и сооружений с такими
соединениями
6.1
42
Материалы болтов, гаек, шайб и покрытий контактных поверхностей
стальных деталей ФПС и опорных поверхностей шайб
42
6.2
Конструктивные требования к соединениям
43
6.3
Подготовка
контактных
поверхностей
элементов
и
методы
контроля
6.4
45
Приготовление и нанесение протекторной грунтовки ВЖС 83-0287. Требования к загрунтованной поверхности. Методы контроля
6.4.1
Основные требования по технике безопасности при работе с
грунтовкой ВЖС 83-02-87
6.4.2
Транспортировка
и
47
хранение
элементов
законсервированных грунтовкой ВЖС 83-02-87
6.5
46
и
деталей,
49
Подготовка и нанесение антифрикционного покрытия на опорные 49
поверхности шайб
6.6
7
Сборка ФПС
49
Список литературы
51
2
3.
31. ВВЕДЕНИЕ
Современный подход к проектированию сооружений, подверженных экстремальным, в
частности, сейсмическим нагрузкам исходит из целенаправленного проектирования предельных
состояний конструкций. В литературе [1, 2, 11, 18] такой подход получил название проектирования
сооружений с заданными параметрами предельных состояний. Возможны различные технические
реализации отмеченного подхода. Во всех случаях в конструкции создаются узлы, в которых от
экстремальных нагрузок могут возникать неупругие смещения элементов. Вследствие этих
смещений нормальная эксплуатация сооружения, как правило, нарушается, однако исключается его
обрушение. Эксплуатационные качества сооружения должны легко восстанавливаться после
экстремальных воздействий. Для обеспечения указанного принципа проектирования и были
предложены фрикционно-подвижные болтовые соединения.
Под
фрикционно-подвижными
соединениями
(ФПС)
понимаются
соединения
металлоконструкций высокопрочными болтами, отличающиеся тем, что отверстия под болты в
соединяемых деталях выполнены овальными вдоль направления действия экстремальных нагрузок.
При экстремальных нагрузках происходит взаимная сдвижка соединяемых деталей на величину до 34 диаметров используемых высокопрочных болтов. Работа таких соединений имеет целый ряд
особенностей и существенно влияет на поведение конструкции в целом. При этом во многих случаях
оказывается возможным снизить затраты на усиление сооружения, подверженного сейсмическим и
другим интенсивным нагрузкам.
ФПС были предложены в НИИ мостов ЛИИЖТа в 1980 г. для реализации принципа
проектирования мостовых конструкций с заданными параметрами предельных состояний. В 1985-86
г.г. эти соединения были защищены авторскими свидетельствами [16-19]. Простейшее стыковое и
нахлесточное соединения приведены на рис.1.1. Как видно из рисунка, от обычных соединений на
высокопрочных болтах предложенные в упомянутых работах отличаются тем, что болты пропущены
через овальные отверстия. По замыслу авторов при экстремальных нагрузках должна происходить
взаимная подвижка соединяемых деталей вдоль овала, и за счет этого уменьшаться пиковое значение
усилий, передаваемое соединением. Соединение с овальными отверстиями применялись в
строительных конструкциях и ранее, например, можно указать предложения [8, 10 и др]. Однако в
упомянутых работах овальные отверстия устраивались с целью упрощения монтажных работ. Для
реализации принципа проектирования конструкций с заданными параметрами предельных состояний
необходимо фиксировать предельную силу трения (несущую способность) соединения.
При использовании обычных болтов их натяжение N не превосходит 80-100 кН, а разброс
натяжения N=20-50 кН, что не позволяет прогнозировать несущую способность такого соединения
по трению. При использовании же высокопрочных болтов при том же N натяжение N= 200 - 400
3
4.
4Рис.1.1. Принципиальная схема фрикционно-подвижного
соединения
а) встык , б) внахлестку
1- соединяемые листы; 2 – высокопрочные болты;
3- шайба;4 – овальные отверстия; 5 – накладки.
кН, что в принципе может позволить задание и регулирование несущей способности соединения.
Именно эту цель преследовали предложения [3,14-17].
Однако проектирование и расчет таких соединений вызвал серьезные трудности. Первые испытания
ФПС показали, что рассматриваемый класс соединений не обеспечивает в общем случае стабильной
работы конструкции. В процессе подвижки возможна заклинка соединения, оплавление контактных
поверхностей соединяемых деталей и т.п. В ряде случаев имели место обрывы головки болта.
Отмеченные
исследования
позволили
выявить
способы
обработки
соединяемых
листов,
обеспечивающих стабильную работу ФПС. В частности, установлена недопустимость использования
для ФПС пескоструйной обработки листов пакета, рекомендованы использование обжига листов,
нанесение на них специальных мастик или напыление мягких металлов. Эти исследования показали,
что расчету и проектированию сооружений должны предшествовать детальные исследования самих
соединений. Однако, до настоящего времени в литературе нет еще систематического изложения
общей теории ФПС даже для одноболтового соединения, отсутствует теория работы многоболтовых
4
5.
5ФПС. Сложившаяся ситуация сдерживает внедрение прогрессивных соединений в практику
строительства.
В силу изложенного можно заключить, что ФПС весьма перспективны для использования в
сейсмостойком строительстве, однако, для этого необходимо детально изложить, а в отдельных
случаях и развить теорию работы таких соединений, методику инженерного расчета самих ФПС и
сооружений с такими соединениями. Целью, предлагаемого пособия является систематическое
изложение теории работы ФПС и практических методов их расчета. В пособии приводится также и
технология монтажа ФПС.
2.ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ И ИЗНОСА
Развитие науки и техники в последние десятилетия показало, что
надежные и долговечные машины, оборудование и приборы могут быть
созданы только при удачном решении теоретических и прикладных задач
сухого и вязкого трения, смазки и износа, т.е. задач трибологии и
триботехники.
Трибология – наука о трении и процессах, сопровождающих трение
(трибос – трение, логос – наука). Трибология охватывает экспериментальнотеоретические
результаты
исследований
физических
(механических,
электрических, магнитных, тепловых), химических, биологических и других
явлений, связанных с трением.
Триботехника
трибологии
при
–
это
система
знаний
проектировании,
о
практическом
изготовлении
и
применении
эксплуатации
трибологических систем.
С
трением
связан
износ
соприкасающихся
тел
–
разрушение
поверхностных слоев деталей подвижных соединений, в т.ч. при резьбовых
соединениях. Качество соединения определяется внешним трением в витках
резьбы и в торце гайки и головки болта (винта) с соприкасающейся деталью
или шайбой. Основная характеристика крепежного резьбового соединения –
усилие затяжки болта (гайки), - зависит от значения и стабильности моментов
5
6.
6сил
трения
сцепления,
возникающих
при
завинчивании.
Момент
сил
сопротивления затяжке содержит две составляющих: одна обусловлена
молекулярным воздействием в зоне фактического касания тел, вторая –
деформированием
тончайших
поверхностей
слоев
контактирующими
микронеровностями взаимодействующих деталей.
Расчет этих составляющих осуществляется по формулам, содержащим ряд
коэффициентов,
установленных
в
результате
экспериментальных
исследований. Сведения об этих формулах содержатся в Справочниках
«Трение, изнашивание и смазка» [22](в двух томах) и «Полимеры в узлах
трения машин и приборах» [13], изданных в 1978-1980 г.г. издательством
«Машиностроение». Эти Справочники не потеряли своей актуальности и
научной обоснованности и в настоящее время. Полезный для практического
использования материал содержится также в монографии Геккера Ф.Р. [5].
Сухое трение. Законы сухого трения
1. Основные понятия: сухое и вязкое трение; внешнее и внутреннее
трение, пограничное трение; виды сухого трения.
Трение – физическое явление, возникающее при относительном движении
соприкасающихся газообразных, жидких и твердых тел и вызывающее
сопротивление движению тел или переходу из состояния покоя в движение
относительно конкретной системы отсчета.
Существует два вида трения: сухое и вязкое.
Сухое трение возникает при соприкосновении твердых тел.
Вязкое трение возникает при движении в жидкой или газообразной среде,
а также при наличии смазки в области механического контакта твердых тел.
При учете трения (сухого или вязкого) различают внешнее трение и
внутренне трение.
Внешнее трение возникает при относительном перемещении двух тел,
находящихся в соприкосновении, при этом сила сопротивления движению
зависит от взаимодействия внешних поверхностей тел и не зависит от
6
7.
7состояния внутренних частей каждого тела. При внешнем трении переход
части механической энергии во внутреннюю энергию тел происходит только
вдоль поверхности раздела взаимодействующих тел.
Внутреннее трение возникает при относительном перемещении частиц
одного и того же тела (твердого, жидкого или газообразного). Например,
внутреннее трение возникает при изгибе металлической пластины или
проволоки, при движении жидкости в трубе (слой жидкости, соприкасающийся
со стенкой трубы, неподвижен, другие слои движутся с разными скоростями и
между ними возникает трение). При внутреннем трении часть механической
энергии переходит во внутреннюю энергию тела.
Внешнее
трение
соприкосновения
в
твердых
чистом
тел
виде
без
возникает
смазочной
только
прослойки
в
между
случае
ними
(идеальный случай). Если толщина смазки 0,1 мм и более, механизм трения не
отличается от механизма внутреннего трения в жидкости. Если толщина
смазки менее 0,1 мм, то трение называют пограничным (или граничным). В
этом случае учет трения ведется либо с позиций сухого трения, либо с точки
зрения вязкого трения (это зависит от требуемой точности результата).
В истории развития понятий о трении первоначально было получено
представление о внешнем трении. Понятие о внутреннем трении введено в
науку в 1867 г. английским физиком, механиком и математиком Уильямом
Томсоном (лордом Кельвиным).1)
Законы сухого трения
Сухое трение впервые наиболее полно изучал Леонардо да Винчи (14521519). В 1519 г. он сформулировал закон трения: сила трения, возникающая
1)
[Томсон (1824-1907) в 10-летнем возрасте был принят в университет в Глазго, после обучения в котором
перешел в Кембриджский университет и закончил его в 21 год; в 22 года он стал профессором математики. В 1896 г.
Томсон был избран почетным членом Петербургской академии наук, а в 1851 г. (в 27 лет) он стал членом Лондонского
королевского общества и 5 лет был его президентом].
7
8.
8при контакте тела с поверхностью другого тела, пропорциональна нагрузке
(силе прижатия тел), при этом коэффициент пропорциональности – величина
постоянная и равна 0,25:
F 0 ,25 N .
Через 180 лет модель Леонарда да Винчи была переоткрыта французским
механиком и физиком Гийомом Амонтоном2), который ввел в науку понятие
коэффициента трения как французской константы и предложил формулу силы
трения скольжения:
F f N.
Кроме того, Амонтон (он изучал равномерное движение тела по наклонной
плоскости) впервые предложил формулу:
f tg
,
где f – коэффициент трения; - угол наклона плоскости к горизонту;
В 1750 г. Леонард Эйлер (1707-1783), придерживаясь закона трения
Леонарда да Винчи – Амонтона:
F f N,
впервые получил формулу для случая прямолинейного равноускоренного
движения тела по наклонной плоскости:
f tg
2S
g t cos 2
2
,
где t – промежуток времени движения тела по плоскости на участке
длиной S;
g – ускорение свободно падающего тела.
Окончательную формулировку законов сухого трения дал в 1781 г. Шарль
Кулон3)
Эти законы используются до сих пор, хотя и были дополнены результатами
работ ученых XIX и XX веков, которые более полно раскрыли понятия силы
2)
Г.Амонтон (1663-1705) – член Французской академии наук с 1699 г.
3) Ш.Кулон (1736-1806) – французский инженер, физик и механик, член Французской академии наук
8
9.
9трения покоя (силы сцепления) и силы трения скольжения, а также понятия о
трении качения и трении верчения.
Многие десятилетия XX века ученые пытались модернизировать законы
Кулона,
учитывая
все
новые
и
новые
результаты
физико-химических
исследований явления трения. Из этих исследований наиболее важными
являются исследования природы трения.
Кратко о природе сухого трения можно сказать следующее. Поверхность
любого
твердого
тела
обладает
[шероховатость
поверхности
классов)
характеристикой
–
микронеровностями,
оценивается
«классом
качества
шероховатостью
шероховатости»
обработки
(14
поверхности:
среднеарифметическим отклонением профиля микронеровностей от средней
линии и высотой неровностей].
Сопротивление сдвигу вершин микронеровностей в зоне контакта тел –
источник трения. К этому добавляются силы молекулярного сцепления между
частицами,
принадлежащими
разным
телам,
вызывающим
прилипание
поверхностей (адгезию) тел.
Работа
внешней
силы,
приложенной
к
телу,
преодолевающей
молекулярное сцепление и деформирующей микронеровности, определяет
механическую энергию тела, которая затрачивается частично на деформацию
(или даже разрушение) микронеровностей, частично на нагревание трущихся
тел (превращается в тепловую энергию), частично на звуковые эффекты –
скрип, шум, потрескивание и т.п. (превращается в акустическую энергию).
В последние годы обнаружено влияние трения на электрическое и
электромагнитное поля молекул и атомов соприкасающихся тел.
Для решения большинства задач классической механики, в которых надо
учесть сухое трение, достаточно использовать те законы сухого трения,
которые открыты Кулоном.
В современной формулировке законы сухого трения (законы Кулона)
даются в следующем виде:
9
10.
10В случае изотропного трения сила трения скольжения тела А по
поверхности тела В всегда направлена в сторону, противоположную скорости
тела А относительно тела В, а сила сцепления (трения покоя) направлена в
сторону, противоположную возможной скорости (рис.2.1, а и б).
Примечание. В случае анизотропного трения линия действия силы трения
скольжения не совпадает с линией действия вектора скорости. (Изотропным
называется сухое трение, характеризующееся одинаковым сопротивлением
движению тела по поверхности другого тела в любом направлении, в
противном случае сухое трение считается анизотропным).
Сила трения скольжения пропорциональна силе давления на опорную
поверхность
(или
нормальной
реакции
этой
поверхности),
при
этом
коэффициент трения скольжения принимается постоянным и определяется
опытным путем для каждой пары соприкасающихся тел. Коэффициент трения
скольжения зависит от рода материала и его физических свойств, а также от
степени обработки поверхностей соприкасающихся тел:
FСК fСК N (рис. 2.1 в).
Y
Y
Fск
tg =fск
N
N
V
Fск
X
G
X
G
N
Fсц
а)
в)
б)
Рис.2.1
Сила сцепления (сила трения покоя) пропорциональна силе давления на
опорную поверхность (или нормальной реакции этой поверхности) и не может
быть
больше
максимального
значения,
10
определяемого
произведением
11.
11коэффициента сцепления на силу давления (или на нормальную реакцию
опорной поверхности):
FСЦ f СЦ N .
Коэффициент сцепления (трения покоя), определяемый опытным путем в
момент перехода тела из состояния покоя в движение, всегда больше
коэффициента трения скольжения для одной и той же пары соприкасающихся
тел:
f СЦ f СК .
Отсюда следует, что:
max
FСЦ
FСК ,
поэтому график изменения силы трения скольжения от времени движения
тела, к которому приложена эта сила, имеет вид (рис.2.2).
При переходе тела из состояния покоя в движение сила трения
max до
скольжения за очень короткий промежуток времени изменяется от FСЦ
FСК (рис.2.2). Этим промежутком времени часто пренебрегают.
В последние десятилетия экспериментально показано, что коэффициент
трения скольжения зависит от скорости (законы Кулона установлены при
равномерном движении тел в диапазоне невысоких скоростей – до 10 м/с).
11
12.
12fсц
max
Fсц
Fск
fск
V
t
V0
Vкр
Рис. 2.2
Рис. 2. 3
Эту зависимость качественно можно проиллюстрировать графиком f СК ( v )
(рис.2.3).
v0
- значение скорости, соответствующее тому моменту времени, когда
сила FСК достигнет своего нормального значения FСК fСК N ,
v КР
- критическое значение скорости, после которого происходит
незначительный рост (на 5-7 %) коэффициента трения скольжения.
Впервые этот эффект установил в 1902 г. немецкий ученый Штрибек (этот
эффект впоследствии был подтвержден исследованиями других ученых).
Российский ученый Б.В.Дерягин, доказывая, что законы Кулона, в
основном, справедливы, на основе адгезионной теории трения предложил
новую формулу для определения силы трения скольжения (модернизировав
предложенную Кулоном формулу):
FСК fСК N S p0 .
[У Кулона: FСК fСК N А , где величина А не раскрыта].
В формуле Дерягина: S – истинная площадь соприкосновения тел
(контактная площадь), р0 - удельная (на единицу площади) сила прилипания
или сцепления, которое надо преодолеть для отрыва одной поверхности от
другой.
Дерягин также показал, что коэффициент трения скольжения зависит от
нагрузки N (при соизмеримости сил N и
S p0
) - fСК ( N ) , причем при
увеличении N он уменьшается (бугорки микронеровностей деформируются и
12
13.
13сглаживаются, поверхности тел становятся менее шероховатыми). Однако,
эта зависимость учитывается только в очень тонких экспериментах при
решении задач особого рода.
Во многих случаях S p0 N , поэтому в задачах классической механики, в
которых следует учесть силу сухого трения, пользуются, в основном, законом
Кулона, а значения коэффициента трения скольжения и коэффициента
сцепления определяют по таблице из справочников физики (эта таблица
содержит значения коэффициентов, установленных еще в 1830-х годах
французским ученым А.Мореном (для наиболее распространенных материалов)
и дополненных более поздними экспериментальными данными. [Артур Морен
(1795-1880) – французский математик и механик, член Парижской академии
наук, автор курса прикладной механики в 3-х частях (1850 г.)].
В случае анизотропного сухого трения линия действия силы трения
скольжения
составляет
с
прямой,
по
которой
направлена
скорость
материальной точки угол:
arctg
Fn
,
Fτ
где Fn и Fτ - проекции силы трения скольжения FCK на главную нормаль и
касательную к траектории материальной точки, при этом модуль вектора FCK
определяется формулой: FCK Fn2 Fτ2 . (Значения Fn и Fτ определяются по
методике Минкина-Доронина).
Трение качения
При качении одного тела по другому участки поверхности одного тела
кратковременно соприкасаются с различными участками поверхности другого
тела, в результате такого контакта тел возникает сопротивление качению.
В конце XIX и в первой половине XX века в разных странах мира были
проведены эксперименты по определению сопротивления качению колеса
13
14.
14вагона или локомотива по рельсу, а также сопротивления качению роликов
или шариков в подшипниках.
В результате экспериментального изучения этого явления установлено,
что сопротивление качению (на примере колеса и рельса) является следствием
трех факторов:
1) вдавливание колеса в рельс вызывает деформацию наружного слоя
соприкасающихся тел (деформация требует затрат энергии);
2)
зацепление
бугорков
неровностей
и
молекулярное
сцепление
(являющиеся в то же время причиной возникновения качения колеса по
рельсу);
3)
трение
скольжения
при
неравномерном
движении
колеса (при
ускоренном или замедленном движении).
(Чистое качение без скольжения – идеализированная модель движения).
Суммарное
влияние
всех
трех
факторов
учитывается
общим
коэффициентом трения качения.
Изучая трение качения, как это впервые сделал Кулон, гипотезу
абсолютно твердого тела надо отбросить и рассматривать деформацию
соприкасающихся тел в области контактной площадки.
Так как равнодействующая N реакций опорной поверхности в точках зоны
контакта смещена в сторону скорости центра колеса, непрерывно набегающего
на впереди лежащее микропрепятствие (распределение реакций в точках
контакта несимметричное – рис.2.4), то возникающая при этом пара сил N и G
C
Vc
N
G
Fск
N
14
K
Рис. 2.4
K
15.
(G15
- сила тяжести) оказывает сопротивление качению (возникновение
качения обязано силе сцепления FСЦ , которая образует вторую составляющую
полной реакции опорной поверхности).
Момент пары сил
N , G
называется моментом сопротивления качению.
Плечо
пары
сил
«к»
называется
коэффициентом трения качения. Он имеет
размерность длины.
Fсопр
Vс
C
Момент
сопротивления
качению
определяется формулой:
MC N k ,
где N - реакция поверхности рельса,
Fсц
N
равная вертикальной нагрузке на колесо с
учетом его веса.
Рис. 2.5
Колесо, катящееся по рельсу, испытывает
сопротивление движению, которое можно отразить силой сопротивления Fсопр ,
приложенной к центру колеса (рис.2.5), при этом: Fсопр R N k , где R – радиус
колеса,
откуда
Fсопр N
k
N h,
R
где h – коэффициент сопротивления, безразмерная величина.
Эту формулу предложил Кулон. Так как множитель h
k
R
во много раз
меньше коэффициента трения скольжения для тех же соприкасающихся тел, то
сила Fсопр на один-два порядка меньше силы трения скольжения. (Это было
известно еще в древности).
Впервые в технике машин это использовал Леонардо да Винчи. Он изобрел
роликовый и шариковый подшипники.
15
16.
Если на рисунке дается картина сил с обозначением силы Fсопр , то силуN
показывают
без
смещения
в
сторону
скорости
(колесо
и
16
рельс
рассматриваются условно как абсолютно твердые тела).
Повышение угловой скорости качения вызывает рост сопротивления
качению. Для колеса железнодорожного экипажа и рельса рост сопротивления
качению заметен после скорости колесной пары 100 км/час и происходит по
параболическому
закону.
Это
объясняется
деформациями
колес
и
гистерезисными потерями, что влияет на коэффициент трения качения.
Трение верчения
Трение верчения возникает при вращении тела,
опирающегося на некоторую поверхность. В этом
случае следует рассматривать зону контакта тел, в
Fск
Fск
r
О
Fск
точках которой возникают силы трения скольжения
FСК (если контакт происходит в одной точке, то
трение верчения отсутствует – идеальный случай)
(рис.2.6).
Рис. 2.6.
А – зона контакта вращающегося тела, ось
вращения которого перпендикулярна к плоскости
этой зоны. Силы трения скольжения, если их привести к центру круга (при
изотропном трении), приводятся к паре сил сопротивления верчению, момент
которой:
М сопр N f ск r ,
где r – средний радиус точек контакта тел;
f ск
- коэффициент трения скольжения (принятый одинаковым для всех
точек и во всех направлениях);
N – реакция опорной поверхности, равная силе давления на эту
поверхность.
16
17.
17Трение верчения наблюдается при вращении оси гироскопа (волчка) или
оси стрелки компаса острием и опорной плоскостью. Момент сопротивления
верчению стремятся уменьшить, используя для острия и опоры агат, рубин,
алмаз и другие хорошо отполированные очень прочные материалы, для
которых коэффициент трения скольжения менее 0,05, при этом радиус круга
опорной площадки достигает долей мм. (В наручных часах, например, М сопр
менее
5 10 5
мм).
Таблица коэффициентов трения скольжения и качения.
к (мм)
f ск
Сталь по стали……0,15
Шарик из закаленной стали по стали……0,01
Сталь по бронзе…..0,11
Мягкая сталь по мягкой стали……………0,05
Железо по чугуну…0,19
Дерево по стали……………………………0,3-0,4
Сталь по льду……..0,027
Резиновая шина по грунтовой дороге……10
Процессы износа контактных поверхностей при трении
Молекулярное
сцепление
приводит
к
образованию
связей
между
трущимися парами. При сдвиге они разрушаются. Из-за шероховатости
поверхностей трения контактирование пар происходит площадками. На
площадках с небольшим давлением имеет место упругая, а с большим
давлением - пластическая деформация. Фактическая площадь соприкасания
пар представляется суммой малых площадок. Размеры площадок контакта
достигают 30-50 мкм. При повышении нагрузки они растут и объединяются. В
процессе разрушения контактных площадок выделяется тепло, и могут
происходить химические реакции.
Различают три группы износа: механический - в форме абразивного
износа, молекулярно-механический - в форме пластической деформации или
хрупкого разрушения и коррозийно-механический - в форме коррозийного и
17
18.
18окислительного износа. Активным фактором износа служит газовая среда,
порождающая
окислительный
износ.
Образование
окисной
пленки
предохраняет пары трения от прямого контакта и схватывания.
Важным фактором является температурный режим пары трения. Теплота
обусловливает физико-химические процессы в слое трения, переводящие
связующие в жидкие фракции, действующие как смазка. Металлокерамические
материалы на железной основе способствуют повышению коэффициента
трения и износостойкости.
Важна быстрая приработка трущихся пар. Это приводит к быстрому
локальному износу и увеличению контурной площади соприкосновения тел.
При
медленной
приработке
локальные
температуры
приводят
к
нежелательным местным изменениям фрикционного материала. Попадание
пыли, песка и других инородных частиц из окружающей среды приводит к
абразивному разрушению не только контактируемого слоя, но и более
глубоких слоев. Чрезмерное давление, превышающее порог схватывания,
приводит к разрушению окисной пленки, местным вырывам материала с
последующим, абразивным разрушением поверхности трения.
Под нагруженностью фрикционной пары понимается совокупность условий
эксплуатации:
давление
поверхностей
трения,
скорость
относительного
скольжения пар, длительность одного цикла нагружения, среднечасовое число
нагружений, температура контактного слоя трения.
Главные требования, предъявляемые к трущимся парам, включают
стабильность коэффициента трения, высокую износостойкость пары трения,
малые модуль упругости и твердость материала, низкий коэффициент
теплового расширения, стабильность физико-химического состава и свойств
поверхностного слоя, хорошая прирабатываемость фрикционного материала,
достаточная механическая прочность, антикоррозийность, несхватываемость,
теплостойкость и другие фрикционные свойства.
18
19.
19Основные факторы нестабильности трения - нарушение технологии
изготовления
деталей,
фрикционных
даже
в
элементов; отклонения
пределах
установленных
размеров отдельных
допусков;
несовершенство
конструктивного исполнения с большой чувствительностью к изменению
коэффициента трения.
Абразивный
износ
фрикционных
пар
подчиняется
следующим
закономерностям. Износ пропорционален пути трения s,
=ks s,
(2.1)
а интенсивность износа— скорости трения
k s v
(2.2)
Износ не зависит от скорости трения, а интенсивность износа на единицу
пути трения пропорциональна удельной нагрузке р,
kp p
s
Мера
(2.3)
интенсивности
износа
рv
не
должна
превосходить
нормы,
определенной на практике (pv<С).
Энергетическая концепция износа состоит в следующем.
Для имеющихся закономерностей износа его величина представляется
интегральной функцией времени или пути трения
t
s
k p pvdt k p pds .
0
(2.4)
0
В условиях кулонова трения, и в случае kр = const, износ пропорционален
работе сил трения W
k w W
kp
f
s
W ; W Fds .
(2.5)
0
Здесь сила трения F=f N = f p ; где f – коэффициент трения, N – сила
нормального давления; - контурная площадь касания пар.
19
20.
Работа сил трения W переходит в тепловую энергию трущихся пар E и20
окружающей среды Q
W=Q+ E.
Работа сил кулонова трения при гармонических колебаниях s == а sin t за
период колебаний Т == 2л/ определяется силой трения F и амплитудой
колебаний а
W= 4F а.
(2.6)
3. МЕТОДИКА РАСЧЕТА ОДНОБОЛТОВЫХ ФПС
3.1. Исходные посылки для разработки методики
расчета ФПС
Исходными посылками для разработки методики расчета ФПС
являются
экспериментальные
исследования
одноболтовых
нахлесточных соединений [13], позволяющие вскрыть основные
особенности работы ФПС.
Для выявления этих особенностей в НИИ мостов в 1990-1991 гг.
были выполнены экспериментальные исследования деформирования
нахлесточных соединений такого типа. Анализ полученных диаграмм
деформирования позволил выделить для них 3 характерных стадии
работы, показанных на рис. 3.1.
На первой стадии нагрузка Т не превышает несущей способности
соединения [Т], рассчитанной как для обычного соединения на
фрикционных высокопрочных болтах.
20
21.
На второй стадии Т > [Т] и происходит преодоление сил трения21
по контактным плоскостям соединяемых элементов при сохраняющих
неподвижность шайбах высокопрочных болтов. При этом за счет
деформации болтов в них растет сила натяжения, и как следствие
растут силы трения по всем плоскостям контактов.
На третьей стадии происходит
срыв с места одной из шайб и
дальнейшее взаимное смещение
соединяемых
элементов.
процессе
В
подвижки
наблюдается интенсивный износ
во
всех
контактных
сопровождающийся
Рис.3.1. Характерная диаграмма деформирования
ФПС
1 – упругая работа ФПС;
2 – стадия проскальзывания листов ФПС при
заклиненных шайбах, характеризующаяся ростом
натяжения болта вследствие его изгибной деформации;
3 – стадия скольжения шайбы болта,
характеризующаяся интенсивным износом контактных
поверхностей.
парах,
падением
натяжения
болтов
и,
следствие,
снижение
как
несущей
способности соединения.
В
процессе
испытаний
наблюдались следующие случаи
выхода из строя ФПС:
• значительные взаимные перемещения соединяемых деталей, в
результате которых болт упирается в край овального отверстия и в
конечном итоге срезается;
• отрыв головки болта вследствие малоцикловой усталости;
• значительные пластические деформации болта, приводящие к
его
необратимому
удлинению
и
исключению
из
работы
при
“обратном ходе" элементов соединения;
• значительный износ контактных поверхностей, приводящий к
ослаблению болта и падению несущей способности ФПС.
21
22.
22Отмеченные
результаты
экспериментальных
исследований
представляют двоякий интерес для описания работы ФПС. С одной
стороны для расчета усилий и перемещений в элементах сооружений
с ФПС важно задать диаграмму деформирования соединения. С
другой стороны необходимо определить возможность перехода ФПС в
предельное состояние.
Для
описания
диаграммы
деформирования
наиболее
существенным представляется факт интенсивного износа трущихся
элементов соединения, приводящий к падению сил натяжения болта
и несущей способности соединения. Этот эффект должен определять
работу как стыковых, так и нахлесточных ФПС. Для нахлесточных
ФПС важным является и дополнительный рост сил натяжения
вследствие деформации болта.
Для оценки возможности перехода соединения в предельное
состояние необходимы следующие проверки:
а) по предельному износу контактных поверхностей;
б) по прочности болта и соединяемых листов на смятие в случае
исчерпания зазора ФПС u0;
в) по несущей способности конструкции в случае удара в момент
закрытия зазора ФПС;
г) по прочности тела болта на разрыв в момент подвижки.
Если учесть известные результаты [11,20,21,26], показывающие,
что закрытие зазора приводит к недопустимому росту ускорений в
конструкции,
то
проверки
(б)
и
(в)
заменяются
проверкой,
ограничивающей перемещения ФПС и величиной фактического
зазора в соединении u0.
Решение вопроса об износе контактных поверхностей ФПС и
подвижке в соединении должно базироваться на задании диаграммы
деформирования
соединения,
представляющей
22
зависимость
его
23.
23несущей способности Т от подвижки в соединении s. Поэтому
получение зависимости Т(s) является основным для разработки
методов
расчета
ФПС
и
сооружений
с
такими
соединениями.
Отмеченные особенности учитываются далее при изложении теории
работы ФПС.
3.2. Общее уравнение для определения несущей
способности ФПС
Для
построения
общего
уравнения
деформирования
ФПС
обратимся к более сложному случаю нахлесточного соединения,
характеризующегося трехстадийной диаграммой деформирования. В
случае стыкового соединения второй участок на диаграмме Т(s) будет
отсутствовать.
Первая стадия работы ФПС не отличается от работы обычных
фрикционных соединений. На второй и третьей стадиях работы
несущая способность соединения поменяется вследствие изменения
натяжения болта. В свою очередь натяжение болта определяется его
деформацией (на второй стадии деформирования нахлесточных
соединений) и износом трущихся поверхностей листов пакета при их
взаимном
смещении.
При
этом
для
теоретического
описания
диаграммы деформирования воспользуемся классической теорией
износа
[5,
14,
23],
согласно
которой
скорость
износа
V
пропорциональна силе нормального давления (натяжения болта) N:
(3.1)
V K N,
где К— коэффициент износа.
В свою очередь силу натяжения болта N можно представить в
виде:
(3.2)
N N0 a N1 N2
23
24.
здесьa
EF
l
N0 -
начальное -натяжение болта, а - жесткость болта;
24
, где l - длина болта, ЕF - его погонная жесткость,
N1 k f ( s ) -
увеличение
натяжения
болта
вследствие
его
деформации;
N2 ( s ) - падение натяжения болта вследствие его пластических
деформаций;
s - величина подвижки в соединении, - износ в соединении.
Для стыковых соединений обе добавки N1 N 2 0 .
Если пренебречь изменением скорости подвижки, то скорость V
можно представить в виде:
V
d d ds
V ср ,
dt
ds dt
(3.3)
где V ср — средняя скорость подвижки.
После подстановки (3.2) в (3.1) с учетом (3.3) получим уравнение:
k a k N0 к f ( s ) ( s ) ,
(3.4)
где k K / Vср .
Решение уравнения (3.4) можно представить в виде:
k N0 a
1
1 e
kas
k e ka( s z ) k f ( z ) ( z ) dz ,
s
0
или
k N0 a
1
e
kas
s
k k f ( z ) ( z ) e kazdz N0 a 1 .
0
(3.5)
3.3. Решение общего уравнения для стыковых ФПС
Для стыковых соединений общий интеграл (3.5) существенно
упрощается, так как в этом случае N 1 N 2 0 , и обращаются в 0
функции
f(z)
и
( z ) ,
входящие в (3.5). С учетом сказанного
24
25.
25использование интеграла. (3.5) позволяет получить следующую
формулу для определения величины износа :
1 e kas k N0 a 1
(3.6)
Падение натяжения N при этом составит:
N 1 e kas k N0 ,
а
(3.7)
несущая
соединений
способность
определяется
по
формуле:
T T0 f N T0 f 1 e kas k N 0 a 1
T0 1 1 e kas k a 1 .
(3.8)
Рис.3.2.Падение несущей способности ФПС в
зависимости от величины подвижки для болта 24
мм при коэффициенте износа k=5 10-8Н-1 для
различной толщины листов пакета l
- l=20 мм; - l=30 мм; - l=40 мм; - l=50 мм;
- l=60 мм; - l=70 мм; - l=40 мм
Как
видно
из
полученной
формулы относительная несущая
способность соединения КТ =Т/Т0
определяется
всего
двумя
параметрами - коэффициентом износа k и жесткостью болта на
растяжение а. Эти параметры могут быть заданы с достаточной
точностью и необходимые для этого данные имеются в справочной
литературе.
На рис. 3.2 приведены зависимости КТ(s) для болта диаметром 24
мм и коэффициента износа k~5×10-8 H-1 при различных значениях
толщины
пакета
l,
определяющей
жесткость болта а. При этом для
наглядности
соединения
начальному
графические
несущая
Т
способность
отнесена
значению
к
T0,
своему
т.е.
зависимости
представлены в безразмерной форме.
Рис.3.3. Падение несущей способности ФПС в
зависимости от величины подвижки для болта
24 мм при коэффициенте износа k=3 10-8Н-1 для
различной толщины листов пакета l
- l=20 мм; - l=30 мм; - l=40 мм;
- l=50 мм; - l=60 мм; - l=70 мм; - l=80 мм
25
26.
26Как видно из рисунка, с ростом толщины пакета падает влияние
износа листов на несущую способность соединений. В целом падение
несущей
способности
соединений
весьма
существенно
и
при
реальных величинах подвижки s 2 3см составляет для стыковых
соединений 80-94%. Весьма существенно на характер падений
несущей способности соединения сказывается коэффициент износа k.
На рис.3.3 приведены зависимости несущей способности соединения
от величины подвижки s при k~3×10-8 H-1.
Исследования показывают, что при k > 2 10-7 Н-1 падение несущей
способности соединения превосходит 50%. Такое падение натяжения
должно приводить к существенному росту взаимных смещений
соединяемых деталей и это обстоятельство должно учитываться в
инженерных расчетах. Вместе с тем рассматриваемый эффект будет
приводить к снижению нагрузки, передаваемой соединением. Это
позволяет при использовании ФПС в качестве сейсмоизолирующего
элемента конструкции рассчитывать усилия в ней, моделируя ФПС
демпфером сухого трения.
3.4. Решение общего уравнения для нахлесточных ФПС
Для нахлесточных ФПС общее решение (3.5) определяется видом
функций f(s) и >(s).Функция f(s) зависит от удлинения болта
вследствие искривления его оси. Если принять для искривленной оси
аппроксимацию в виде:
u( x ) s sin
x
2l
(3.9)
,
где x — расстояние от середины болта до рассматриваемой точки
(рис. 3.3), то длина искривленной оси стержня составит:
26
27.
271
L
2
1
1
2
1
2
2
du
1 dx
dx
1
s 2 2
1
2
2
cos
8l 2 1
2
x
2l
1 s
2
4l
cos
2l
1
dx
2
dx 1
2 2
1 s cos x dx
8l 2
2l
1
2
2
s 2 2
.
8l
Удлинение болта при этом определится по формуле:
s 2 2
l L l
.
8l
Учитывая,
(3.10)
что
приближенность
представления
(3.9)
компенсируется коэффициентом k, который может быть определен из
экспериментальных данных, получим следующее представление для
f(s):
2
f(s) s
l
.
Для дальнейшего необходимо учесть, что деформирование тела
болта будет иметь место лишь до момента срыва его головки, т.е. при
s < s0. Для записи этого факта воспользуемся единичной функцией
Хевисайда :
s2
f ( s ) ( s s0 ).
l
(3.11)
Перейдем теперь к заданию функции (s). При этом необходимо
учесть следующие ее свойства:
1. пластика проявляется лишь при превышении подвижкой s
некоторой величины Sпл, т.е. при Sпл<s<S0.
2. предельное натяжение стержня не превосходит усилия Nт, при
котором напряжения в стержне достигнут предела текучести,
т.е.:
lim ( N0 кf ( s ) ( s )) 0 .
(3.12)
s
Указанным условиям удовлетворяет функция (s) следующего
вида:
27
28.
( s ) N пл ( NТ N пл ) ( 1 eq( s S пл )
28
) 1 ( s s0 ) ( s S пл ).
(3.13)
Подстановка выражений (3.11, 3.12) в интеграл (3.5) приводит к
следующим зависимостям износа листов пакета от перемещения s:
при s<Sпл
s
N0
k
2
2
( 1 e k1as ) s 2
s
1 e k1as
2
a
al
k1a
k1a
,
(3.14)
при Sпл< s<S0
( s ) I ( Sпл ) k1(
),
NT
N N пл
1 ek1a( S пл s ) T
k1a
k1 a
(3.15)
e ( S пл s ) ek1a( S пл s )
при s<S0
( s ) II ( S0 )
N ( S0 )
( 1 e k 2 a( s S0 ) ).
a
Несущая
способность
(3.16)
соединения
определяется
при
этом
выражением:
(3.17)
T T0 fv a .
Здесь fv— коэффициент трения, зависящий в общем случае от
скорости
подвижки
v.
Ниже
мы
используем
наиболее
распространенную зависимость коэффициента трения от скорости,
записываемую в виде:
f
f0
,
1 kvV
(3.18)
где kv — постоянный коэффициент.
Предложенная
зависимость
содержит
9
неопределенных
параметров:
k1, k2, kv, S0, Sпл, q, f0, N0, и k0. Эти параметры должны
определяться из данных эксперимента.
В отличие от стыковых соединений в формуле (3.17) введено два
коэффициента
износа
-
на
втором
участке
диаграммы
деформирования износ определяется трением между листами пакета
28
29.
и характеризуется коэффициентом износа k1, на третьем участке29
износ определяется трением между шайбой болта и наружным
листом пакета; для его описания введен коэффициент износа k2.
На
рис.
3.4
приведен
пример
теоретической
диаграммы
деформирования при реальных значениях параметров k1 = 0.00001;
k2 =0.000016; kv = 0.15; S0 = 10 мм; Sпл = 4 мм; f0 = 0.3; N0 = 300 кН.
Как видно из рисунка, теоретическая диаграмма деформирования
соответствует описанным выше экспериментальным диаграммам.
Рис. 3.4
Теоретическая диаграмма деформирования ФПС
29
30.
2630
4. АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ
ИССЛЕДОВАНИЙ РАБОТЫ ФПС
Для анализа работы ФПС и сооружений с такими соединениями необходимы
фактические
данные
о
параметрах
исследуемых
соединений.
Экспериментальные
исследования работы ФПС достаточно трудоемки, однако в 1980-85 гг. такие исследования
были начаты в НИИ мостов А.Ю.Симкиным [3,11]. В частности, были получены записи Т(s)
для нескольких одноболтовых и четырехболтовых соединений.
Для анализа поведения ФПС были испытаны соединения с болтами диаметром 22, 24,
27 и 48 мм. Принятые размеры образцов обусловлены тем, что диаметры 22, 24 и 27 мм
являются наиболее распространенными. Однако при этом в соединении необходимо
размещение слишком большого количества болтов, и соединение становится громоздким.
Для уменьшения числа болтов необходимо увеличение их диаметра. Поэтому было
рассмотрено ФПС с болтами наибольшего диаметра 48 мм. Общий вид образцов показан на
рис. 4.1.
Рис. 4.1 Общий вид образцов ПС с болтами 48 мм
Пластины ФПС были выполнены из толстолистовой стали марки 10ХСНД.
Высокопрочные болты были изготовлены тензометрическими из стали 40Х "селект" в
соответствии с требованиями [6]. Контактные поверхности пластин были обработаны
протекторной цинкосодержащей грунтовкой ВЖС-41 после дробеструйной очистки. Болты
были предварительно протарированы с помощью электронного пульта АИ-1 и при сборке
соединений натягивались по этому же пульту в соответствии с тарировочными
зависимостями ручным ключом на заданное усилие натяжения N0.
30
4.
31.
31АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ
ИССЛЕДОВАНИЙ РАБОТЫ ФПС
Для анализа работы ФПС и сооружений с такими соединениями
необходимы
соединений.
фактические
данные
Экспериментальные
о
параметрах
исследования
исследуемых
работы
ФПС
достаточно трудоемки, однако в 1980-85 гг. такие исследования были
начаты в НИИ мостов А.Ю.Симкиным [3,11]. В частности, были
получены
записи
Т(s)
для
нескольких
одноболтовых
и
четырехболтовых соединений.
Для анализа поведения ФПС были испытаны соединения с
болтами диаметром 22, 24, 27 и 48 мм. Принятые размеры образцов
обусловлены тем, что диаметры 22, 24 и 27 мм являются наиболее
Рис. 4.1 Общий вид образцов ПС с болтами 48 мм
распространенными. Однако при этом в соединении необходимо
размещение слишком большого количества болтов, и соединение
становится громоздким. Для уменьшения числа болтов необходимо
увеличение их диаметра. Поэтому было рассмотрено ФПС с болтами
31
32.
32наибольшего диаметра 48 мм. Общий вид образцов показан на рис.
4.1.
Пластины ФПС были выполнены из толстолистовой стали марки
10ХСНД.
Высокопрочные
тензометрическими
требованиями
из
[6].
стали
болты
40Х
Контактные
были
"селект"
в
поверхности
изготовлены
соответствии
пластин
с
были
обработаны протекторной цинкосодержащей грунтовкой ВЖС-41
после
дробеструйной
очистки.
Болты
были
предварительно
протарированы с помощью электронного пульта АИ-1 и при сборке
соединений натягивались по этому же пульту в соответствии с
тарировочными зависимостями ручным ключом на заданное усилие
натяжения N0.
Испытания проводились на пульсаторах в НИИ мостов и на
универсальном динамическом стенде УДС-100 экспериментальной
базы ЛВВИСКУ. В испытаниях на стенде импульсная нагрузка на ФПС
обеспечивалась путем удара движущейся массы М через резиновую
прокладку в рабочую тележку, связанную с ФПС жесткой тягой.
Масса и скорость тележки, а также жесткость прокладки подбирались
таким образом, чтобы при неподвижной рабочей тележке получился
импульс силы с участком, на котором сила сохраняет постоянное
значение, длительностью около 150 мс. Амплитудное значение
импульса силы подбиралось из условия некоторого превышения
несущей способности ФПС. Каждый образец доводился до реализации
полного смещения по овальному отверстию.
Во
время
испытаний
на
стенде
и
пресс-пульсаторах
контролировались следующие параметры:
• величина динамической продольной силы в пакете ФПС;
• взаимное смещение пластин ФПС;
• абсолютные скорости сдвига пластин ФПС;
32
33.
33• ускорение движения пластин ФПС и ударные массы (для
испытаний на стенде).
После
каждого
нагружения
проводился
замер
напряжения
высокопрочного болта.
Из полученных в результате замеров данных наибольший интерес
представляют для нас зависимости продольной силы, передаваемой
на соединение (несущей способности ФПС), от величины подвижки S.
Эти зависимости могут быть получены теоретически по формулам,
приведенным выше в разделе 3. На рисунках 4.2 - 4.3 приведено
графическое
Рис. 4.2, 4.3 Экспериментальные диаграммы деформирования ФПС для
болтов 22 мм и 24 мм.
представление полученных диаграмм деформирования ФПС. Из
рисунков видно, что характер зависимостей Т(s) соответствует в
целом принятым гипотезам и результатам теоретических построений
предыдущего раздела. В частности, четко проявляются три участка
деформирования
соединения,
соединения:
после
до
проскальзывания
проскальзывания
листов
элементов
пакета
и
после
проскальзывания шайбы относительно наружного листа пакета.
Вместе
с
тем,
необходимо
отметить
существенный
разброс
полученных диаграмм. Это связано, по-видимому, с тем, что в
33
34.
34проведенных испытаниях принят наиболее простой приемлемый
способ обработки листов пакета. Несмотря на наличие существенного
разброса,
полученные
диаграммы
оказались
пригодными
для
дальнейшей обработки.
В результате предварительной обработки экспериментальных
данных построены диаграммы деформирования нахлесточных ФПС. В
соответствии с ранее изложенными теоретическими разработками
эти диаграммы должны описываться уравнениями вида (3.14). В
указанные уравнения входят 9 параметров:
N0— начальное натяжение; f0 — коэффициент трения покоя;
k0
—
коэффициент,
определяющий
влияние
скорости
на
коэффициент трения скольжения;
k1— коэффициент износа по контакту трущихся листов пакета;
k2— коэффициент износа по контакту листа и шайбы;
Sпл
—
предельное
смещение,
при
котором
возникают
пластические деформации в теле болта;
S0— предельное смещение, при котором возникает срыв шайбы
болта относительно листа пакета;
к — коэффициент, характеризующий увеличение натяжения
болта вследствие геометрической нелинейности его работы;
q — коэффициент, характеризующий уменьшение натяжения
болта вследствие его пластической работы.
Обработка
экспериментальных
данных
заключалась
в
определении этих 9 параметров. При этом параметры варьировались
на сетке их возможных значений. Для каждой девятки значений
параметров по методу наименьших квадратов вычислялась величина
невязки
между
деформирования,
расчетной
причем
и
экспериментальной
невязка
суммировалась
цифровки экспериментальной диаграммы.
34
диаграммами
по
точкам
35.
35Для
поиска
искомых
значений
параметров
для
болтов
диаметром 24 мм последние варьировались в следующих пределах:
k1, k2— от 0.000001 до 0.00001 с шагом 0.000001 Н; kv— от 0 до 1 с
шагом 0.1 с/мм;
S0 — от величины Sпл до 25 с шагом 1 мм; Sпл — от 1 до 10 с шагом
1 мм;
q— от 0.1 до 1 с шагом 0.1 мм~1; f0— от 0.1 до 0.5 с шагом 0.05;
N0— от 30 до 60 с шагом 5 кН; к — от 0.1 до 1 с шагом 0.1;
Н
а рис.
4.4 и
4.5
приве
дены
харак
терн
Рис. 4.5
Рис.4.4
ые
диаграммы деформирования ФПС, полученные экспериментально и
соответствующие
им
теоретические
диаграммы.
Сопоставление
расчетных и натурных данных указывают на то, что подбором
параметров ФПС удается добиться хорошего совпадения натурных и
расчетных диаграмм деформирования ФПС. Расхождение диаграмм
на конечном их участке обусловлено резким падением скорости
подвижки
перед
остановкой,
не
учитываемым
в
рамках
предложенной теории расчета ФПС. Для болтов диаметром 24 мм
было обработано 8 экспериментальных диаграмм деформирования.
Результаты определения параметров соединения для каждой из
подвижек приведены в таблице 4.1.
Таблица 4.1
35
36.
36Результаты определения параметров ФПС
параметры k1106, k2
k ,
S0, SПЛ
q,
f0 N0, к
1
6
-1
N подвижки кН10 , с/мм мм мм мм
кН
1
кН1
11
32
0.25 11
9 0.0000 0.34 105 260
2
8
15
0,24 8
7 0.0004
0.36 152 90
1
3
12
27
0.44 13.5 11.2 0.0001
0.39 125 230
4
4
7
14
0.42 14.6 12 0.0001
0.29 193 130
2
5
14
35
0.1
8 4.2 0.0006
0.3 370 310
1
6
6
11
0.2 12
9 0.0000 0.3 120 100
7
8
20
0.2 19 16 0.0000
0.3 106 130
2
8
8
15
0.3
9 2.5 0.0002
0.35 154 75
1
8
Приведенные в таблице 4.1 результаты вычислений параметров
соединения
были
статистически
обработаны
и
получены
математические ожидания и среднеквадратичные отклонения для
каждого из параметров. Их значения приведены в таблице 4.2. Как
видно
из
приведенной
таблицы,
значения
параметров
характеризуются значительным разбросом. Этот факт затрудняет
применение
одноболтовых
ФПС
с
поверхности (обжиг листов пакета).
одноболтовых
к
многоболтовым
рассмотренной
обработкой
Вместе с тем, переход от
соединениям
должен
снижать
разброс в параметрах диаграммы деформирования.
Таблица. 4.2.
Результаты статистической обработки значений параметров ФПС
Значения параметров
Параметры
математическо среднеквадратичн
соединени
е
ое
6я
1
ожидание
отклонение
k1 10 , КН9.25
2.76
6
1
k2 10 , кН21.13
9.06
kv с/мм
0.269
0.115
S0, мм
11.89
3.78
Sпл , мм
8.86
4.32
-1
q, мм
0.00019
0.00022
f0
0.329
0.036
Nо,кН
165.6
87.7
36
37.
37165.6
88.38
5. ОЦЕНКА ПАРАМЕТРОВ ДИАГРАММЫ
ДЕФОРМИРОВАНИЯ МНОГОБОЛТОВЫХ
ФРИКЦИОННО-ПОДВИЖНЫХ СОЕДИНЕНИЙ (ФПС)
5.1. Общие положения методики расчета
многоболтовых ФПС
Имеющиеся теоретические и экспериментальные исследования
одноболтовых ФПС позволяют перейти к анализу многоболтовых
соединений. Для упрощения задачи примем широко используемое в
исследованиях фрикционных болтовых соединений предположение о
том, что болты в соединении работают независимо. В этом случае
математическое ожидание несущей способности T и дисперсию DT
(или среднеквадратическое отклонение T ) можно записать в виде:
T( s )
DT
T ( s , 1 , 2 ,... k ) p1( 1 ) p2 ( 2 )... pk ( k )d 1d 2 ...d k
(T T )
2
p1 p2 ... pk d 1d 2 ...d k
... T 2 p1 p2 ... pk d 1d 2 ...d k
(5.1)
(5.2)
T
2
T DT
(5.3)
В приведенных формулах:
T ( s , 1 , 2 ,... k ) - найденная выше зависимость несущей способности
T от подвижки s и параметров соединения i; в нашем случае в
37
38.
38качестве параметров выступают коэффициент износа k, смещение
при срыве соединения S0 и др.
pi(ai) — функция плотности распределения i-го параметра; по
имеющимся данным нам известны лишь среднее значение i
и их
стандарт (дисперсия).
Для дальнейших исследований приняты два возможных закона
распределения
возможном
параметров
диапазоне
ФПС:
равномерное
изменения
параметров
в
некотором
и
min i max
нормальное. Если учесть, что в предыдущих исследованиях получены
величины
математических
ожиданий
i и
стандарта
i ,
то
соответствующие функции плотности распределения записываются в
виде:
а) для равномерного распределения
pi
1
при 3 3
2 i 3
(5.4)
и pi = 0 в остальных случаях;
б) для нормального распределения
pi
1
i 2
2
i ai
e
2 i 2
(5.5)
.
Результаты расчетного определения зависимостей T(s) и (s) при
двух законах распределения сопоставляются между собой, а также с
данными натурных испытаний двух, четырех, и восьми болтовых
ФПС.
5.2. Построение уравнений деформирования стыковых
многоболтовых ФПС
38
39.
39Для вычисления несущей способности соединения сначала
рассматривается более простое соединение встык. Такое соединение
характеризуется всего двумя параметрами - начальной несущей
способностью Т0 и коэффициентом износа k. При этом несущая
способность одноболтового соединения описывается уравнением:
T=Toe-kas .
(5.6)
В случае равномерного распределения математическое ожидание
несущей способности соединения из п болтов составит:
k T 3
dk
dT
kas
T
e
2 k 3 2 T 3
3 k T 3
T0 T 3
T n
T0 T
nT0 e kas
При
sh( sa k 3 )
sa k
(5.7)
.
нормальном
законе
распределения
математическое
ожидание несущей способности соединения из п болтов определится
следующим образом:
T n
Te
1
kas
T 2
( T T ) 2
e
2 T 2
1
k 2
( k k )2
e
2 k 2
dkdT
( k k )2
( T T ) 2
1
1
2 k 2
2 T 2
kas
n
Te
dT
e
e
dk
.
2
2
T
k
Если
учесть,
математическим
что
для
ожиданием
любой
случайной
функцией
x
величины
распределения
x
с
р(х}
выполняется соотношение:
x
x p( x ) dx ,
то первая скобка. в описанном выражении для вычисления
несущей
способности
соединения
Т
равна
математическому
ожиданию начальной несущей способности Т0. При этом:
39
40.
40T nT0
kas
1
k 2
( k k )2
2 k 2
e
dk .
Выделяя в показателе степени полученного выражения полный
квадрат, получим:
T nT0
nT0
1
k 2
1
k 2
k k as k2 2 as k as k2
2 k2
e
2
dk
2
as 2
k k as k2
k
as k
2
2 k2
e
e
dk .
Подынтегральный член в полученном выражении с учетом
1
множителя
k 2
представляет не что иное, как функцию плотности
нормального распределения с математическим ожиданием k as k2 и
среднеквадратичным отклонением k . По этой причине интеграл в
полученном выражении тождественно равен 1
и выражение для
несущей способности соединения принимает окончательный вид:
T nT0 e
ask
a 2 s 2 k2
2
.
(5.8)
Соответствующие принятым законам распределения дисперсии
составляют:
для равномерного закона распределения
T2
2
1 2 F ( 2 x ) F ( x ) ,
T0
2 2 ask
D nT0 e
где F ( x )
(5.9)
shx
; x sa k 3
x
для нормального закона распределения
2
2
2 1 A
A1
2
D n T0 T 1 ( A1 ) e T0 e 1 ( A ) ,
2
40
(5.10)
41.
41где
A1 2 as( k2 as k ).
Представляет интерес сопоставить полученные зависимости с
аналогичными
зависимостями,
выведенными
выше
для
одноболтовых соединений.
Рассмотрим,
прежде
всего,
характер
изменения
несущей
способности ФПС по мере увеличения подвижки s и коэффициента
k
износа
для
случая
использования
равномерного
закона
распределения в соответствии с формулой (5.4). Для этого введем по
аналогии с (5.4) безразмерные характеристики изменения несущей
способности:
относительное падение несущей способности
sh( x )
kas
T
x
1
e
nT0
(5.11)
.
коэффициент перехода от одноболтового к многоболтовому
соединению
T
1
nT0 e
kas
Наконец
sh( x )
.
x
для
(5.12)
относительной
величины
среднеквадратичного
отклонения с с использованием формулы (5.9) нетрудно получить
1
nT0 e kas
2
1
T2 sh2 x shx
1
.
2 2 x
n
x
T0
(5.13)
Аналогичные зависимости получаются и для случая нормального
распределения:
2
1 A
e 1 ( A ) ,
2
(5.14)
2 2
k s
1 2 kas
2 e
1 ( A )
2
,
(5.15)
41
42.
422
T2
1
1
2
n
T0
2
1 ( A ) e A1 1 e A 1 ( A ) ,
1
2
(5.16)
где
k2 s 2
A
2 s ka ,
2
A1 2 As ( k2 sa k ) ,
( A )
2
A
2
z
e dz .
0
На рис. 5.1 - 5.2 приведены зависимости i и i от величины
подвижки s. Кривые построены при тех же значениях переменных,
что использовались нами ранее при построении зависимости T/T0 для
одноболтового соединения. Как видно из рисунков, зависимости i ( k , s )
аналогичны
зависимостям,
полученным
для
одноболтовых
соединений, но характеризуются большей плавностью, что должно
благоприятно сказываться на работе соединения и конструкции в
целом.
Особый интерес представляет с нашей точки зрения зависимость коэффициента перехода
i ( k , a , s ) . По своему смыслу математическое ожидание несущей способности многоболтового
соединения T получается из несущей способности одноболтового соединения Т1 умножением на ,
т.е.:
T T1
(5.17)
Согласно (5.12) lim x 1 . В частности, 1 при неограниченном увеличении
математического ожидания коэффициента износа k или смещения s. Более того, при выполнении
условия
k k 3
(5.18)
будет иметь место неограниченный рост несущей способности ФПС с увеличением подвижки s,
что противоречит смыслу задачи.
Полученный результат ограничивает возможность применения равномерного распределения
условием (5.18).
Что касается нормального распределения, то возможность его применения определяется
пределом:
lim 2
s
1
lim e ( kas A ) 1 ( A ) .
2 s
42
43.
43Для анализа этого предела учтем известное в теории вероятности соотношение:
x2
1 2 1
lim 1 x lim
e
.
x
x
x
2
43
44.
441=
а)
2=Т/nT0
S, мм
Подвижка S, мм
Рис.5.1. Графики зависимости расчетного снижения несущей способности ФПС от величины
подвижки в соединении при различной толщине пакета листов l
а) при использовании равномерного закона распределения параметров ФПС
б) при использовании нормального закона распределения параметров ФПС
● - l=20мм; ▼ - l=30мм; □ - l=40мм; - l=50мм; - l=60мм; ○ - l=70мм; - l=80мм;
44
45.
451
а)
S, мм
Коэффициент перехода 2
б)
Подвижка S, мм
Рис.5.2. Графики зависимости коэффициента перехода от одноболтового к многоболтовому ФПС
от величины подвижки в соединении при различной толщине пакета листов l
а) при использовании равномерного закона распределения параметров ФПС
б) при использовании нормального закона распределения параметров ФПС
● - l=20мм; - l=30мм; □ - l=40мм; - l=50мм; - l=60мм; ○ - l=70мм; - l=80мм
С учетом сказанного получим:
45
46.
461 kas A
1
e
s 2
2
lim 2 lim
s
A2
e 2
1
0.
A
(5.19)
Предел (5.19) указывает на возможность применения нормального закона распределения при
любых соотношениях k и k.
Результаты обработки экспериментальных исследований, выполненные ранее, показывают, что
разброс значений несущей способности ФПС для случая обработки поверхностей соединяемых
листов путем нанесения грунтовки ВЖС достаточно велик и достигает 50%. Однако даже в этом
случае применение ФПС вполне приемлемо, если перейти от одноболтовых к многоболтовым
соединениям. Как следует из полученных формул (5.13, 5.16), для среднеквадратичного отклонения
1 последнее убывает пропорционально корню из числа болтов.
На рисунке 5.3 приведена
зависимость относительной величины среднеквадратичного отклонения 1 от безразмерного
параметра х для безразмерной подвижки 2-х, 4-х, 9-ти и 16-ти болтового соединений. Значения T и
T0 приняты в соответствии с данными выполненных экспериментальных исследований. Как видно из
графика, уже для 9-ти болтового соединения разброс значений несущей способности Т не
превосходит 25%, что следует считать вполне приемлемым.
Рис.5.3. Зависимость относительного разброса несущей
способности ФПС от величины подвижки при различном
числе болтов n
46
47.
475.3. Построение уравнений деформирования
нахлесточных многоболтовых соединений
Распространение использованного выше подхода на расчет нахлесточных соединений
достаточно громоздко из-за большого количества случайных параметров, определяющих работу
соединения. Однако с практической точки зрения представляется важным учесть лишь
максимальную силу трения Тmax, смещение при срыве соединения S0 и коэффициент износа k. При
этом диаграмма деформирования соединения между точками (0,Т0) и (S0, Tmax) аппроксимируется
линейной зависимостью. Для учета излома графика T(S) в точке S0 введена функция :
1 при 0 S S 0
0 при S S 0
S , S 0
(5.20)
При этом диаграмма нагружения ФПС описывается уравнением:
T ( S ) T1( S , S0 ,T0 ,Tmax ) ( S , S0 ) T2 ( S ,Tmax ,k , S0 ) 1 ( S , S0 ) ,
где T1( S ) T0 ( Tmax T0 )
S
,
S0
(5.21)
T2 ( S ) Tmax e ka( S S0 ) .
Математическое ожидание несущей способности нахлесточного соединения из n болтов
определяется следующим интегралом:
T n
T
( S ) p( k ) p( S0 ) p( Tmax ) dk dS0 dT0 dTmax n I 1 I 2
(5.22)
k S0 T0 Tmax
Обратимся сначала к вычислению первого интеграла. После подстановки в (5.22)
представления для Т1 согласно (5.20) интеграл I1 может быть представлен в виде суммы трех
интегралов:
s
T0 ( Tmax T0 ) s , S 0 p( S 0 ) p( T0 ) p( Tmax )
S0
S0 T0 Tmax
dS 0 dT0 dTmax I 1,1 I 1,2 I 1,3
I1
(5.23)
где
I1,1
T0 p( T0 ) ( s ,S0 )p( S0 ) p( T0 ) p( Tmax )dTmax dS0 dT0
S0 T0 Tmax
T0 p( T0 )dT0 s , S0 p( S0 )dS0 Tmax p( Tmax )dTmax
T0
S0
Tmax
Если учесть, что для любой случайной величины x выполняются соотношения:
47
48.
48p( x )dx 1
и
xp( x )dx x ,
то получим
I 1,1 T ( s , S0 )p( S0 ) dS0 .
S0
Аналогично
I1,2
Tmax
S0 T0 Tmax
T max
( s , S0 )
S0
S0
I1,3
T0
S0 T0 Tmax
T0
( s , S0 )
S0
S0
s
( s , S0 )p( S0 ) p( T0 ) p( Tmax ) dS0 dT0 dTmax
S0
p( S0 ) dS0 .
s
( s , S0 )p( S0 ) p( T0 ) p( Tmax ) dS0 dT0 dTmax
S0
p( S0 ) dS0 .
Если ввести функции
1 ( s ) ( s , S 0 ) p( S 0 ) dS0
(5.24)
и
1( s )
( s , S0 )
S0
p( S 0 ) dS0 ,
(5.25)
то интеграл I1 можно представить в виде:
I 1 T 1( s ) ( T max T 0 )s 2 ( s ).
(5.26)
Если учесть, что на первом участке s < S0, то с учетом (5.20) формулы (5.24) и (5.25) упростятся
и примут вид:
1( s ) p( S0 )dS0
(5.27)
s
2( s )
s
p( S0 )
dS0 .
S0
(5.28)
Для нормального распределения p(S0) функция 1 1 erf ( s ) , а
функция записывается в виде:
48
49.
49( S0 S 0
2
s
e
)2
2 s2
(5.29)
dS0 .
S0
Для равномерного распределения функции 1 и 2 могут быть
представлены аналитически:
1 при s S 0 s 3
1 S0 s 3 s при S 0 s 3 s S 0 s 3
0 при s S 0 s 3 .
(5.30)
S0 s 3
1
ln
при s S 0 s 3
2 s 3 S 0 s 3
S0 s 3
1
2
ln
при S 0 s 3 s S 0 s 3
s
2 s 3
0 при s S 0 s 3
Аналитическое
представление
для
(5.31)
интеграла
(5.23)
весьма
сложно. Для большинства видов распределений его целесообразно
табулировать; для равномерного распределения интегралы I1 и I2
представляются в замкнутой форме:
S0 s 3
S
ln
при S S 0 s 3
T 0 ( T max T 0 )
2 s 3 S 0 s 3
S0 s 3
S0 s 3
1
( T max T 0 )S ln
I1
T 0 S 0 s 3 S ln
(5.32)
s
s
2 s 3
при S 0 s 3 S S 0 s 3
0 при S S 0 3
s
0 при S S 0 s 3
I2 T m
F( S ) F( s 3 )
2 s 3
при
(5.33)
S S0 s 3,
причем F ( x ) Ei ax( k k 3 ) Ei ax( k k 3 ) . В формулах (5.32, 5.33)
Ei - интегральная показательная функция.
49
50.
50Полученные
экспериментальных
формулы
подтверждены
исследований
многоболтовых
результатами
соединений
и
рекомендуются к использованию при проектировании сейсмостойких
конструкций с ФПС.
50
51.
4251
6. РЕКОМЕНДАЦИИ ПО ТЕХНОЛОГИИ
ИЗГОТОВЛЕНИЯ ФПС И СООРУЖЕНИЙ С
ТАКИМИ СОЕДИНЕНИЯМИ
Технология изготовления ФПС включает выбор материала элементов соединения,
подготовку контактных поверхностей, транспортировку и хранение деталей, сборку
соединений. Эти вопросы освещены ниже.
6.1. Материалы болтов, гаек, шайб и покрытий
контактных поверхностей стальных деталей ФПС
и опорных поверхностей шайб
Для ФПС следует применять высокопрочные болты по ГОСТ 553-77, гайки по ГОСТ
22354-74, шайбы по ГОСТ 22355-75 с обработкой опорной поверхности по указаниям
раздела 6.4 настоящего пособия. Основные размеры в мм болтов, гаек и шайб и расчетные
площади поперечных сечений в мм2 приведены в табл.6.1.
Таблица 6.1.
Номиналь
Расчетная
Высота
Высота
ный
площадь
головки
гайки
12
15
диаметр по сечения
телу по резьбе
по
болта
16
201
157
Размер
Диаметр
Размеры шайб
Толщина
Диаметр
под ключ опис.окр.
внутр.
нар.
гайки
27
29,9
4
18
37
18
255
192
13
16
30
33,3
4
20
39
20
314
245
14
18
32
35,0
4
22
44
22
380
303
15
19
36
39,6
6
24
50
24
453
352
17
22
41
45,2
6
26
56
27
573
459
19
24
46
50,9
6
30
66
30
707
560
19
24
46
50,9
6
30
66
36
1018
816
23
29
55
60,8
6
39
78
42
1386
1120
26
34
65
72,1
8
45
90
48
1810
1472
30
38
75
83,4
8
52
100
Полная длина болтов в случае использования шайб по ГОС 22355-75 назначается в
соответствии с данными табл.6.2.
6.
51
52.
52РЕКОМЕНДАЦИИ ПО ТЕХНОЛОГИИ ИЗГОТОВЛЕНИЯ ФПС
И СООРУЖЕНИЙ С ТАКИМИ СОЕДИНЕНИЯМИ
Технология
элементов
изготовления
соединения,
транспортировку
и
ФПС
включает
подготовку
хранение
выбор
контактных
деталей,
сборку
материала
поверхностей,
соединений.
Эти
вопросы освещены ниже.
6.1.Материалы болтов, гаек, шайб и покрытий
контактных поверхностей стальных деталей ФПС и
опорных поверхностей шайб
Для ФПС следует применять высокопрочные болты по ГОСТ 55377, гайки по ГОСТ 22354-74, шайбы по ГОСТ 22355-75 с обработкой
опорной поверхности по указаниям раздела 6.4 настоящего пособия.
Основные размеры в мм болтов, гаек и шайб и расчетные площади
поперечных сечений в мм2 приведены в табл.6.1.
Таблица 6.1.
Номина Расчетная
льный
диаметр
болта
Высота Высот Разме Диамет
площадь головк
сечения
и
а
р под
р
Размеры шайб
Диаметр
внут
нар.
на
Толщи
гайки ключ опис.ок
по
р.
р. гайки
по телу по
16
201 резьбе
157
12
15
27
29,9
4
18
37
18
255 192
13
16
30
33,3
4
20
39
20
314 245
14
18
32
35,0
4
22
44
22
380 303
15
19
36
39,6
6
24
50
24
453 352
17
22
41
45,2
6
26
56
52
53.
5327
573 459
19
24
46
50,9
6
30
66
30
707 560
19
24
46
50,9
6
30
66
36
1018 816
23
29
55
60,8
6
39
78
42
1386 1120
26
34
65
72,1
8
45
90
48
1810 1472
30
38
75
83,4
8
52
100
Полная длина болтов в случае использования шайб по ГОС 2235575 назначается в соответствии с данными табл.6.2.
Таблица 6.2.
Номинальна Длина резьбы 10 при номинальном диаметре
16 18 20 22 24 27 30 36 42 48
я
длина резьбы d
40
*
45
38 *
стержня
50
38 42 *
55
38 42 46 *
60
38 42 46 50 *
65
38 42 46 50 54
70
38 42 46 50 54 60
75
38 42 46 50 54 60 66
80
38 42 46 50 54 60 66
85
38 42 46 50 54 60 66
90
38 42 46 50 54 60 66 78
95
38 42 46 50 54 60 66 78
100
38 42 46 50 54 60 66 78
105
38 42 46 50 54 60 66 78 90
110
38 42 46 50 54 60 66 78 90 102
115
38 42 46 50 54 60 66 78 90 102
120
38 42 46 50 54 60 66 78 90 102
125
38 42 46 50 54 60 66 78 90 102
130
38 42 46 50 54 60 66 78 90 102
140
38 42 46 50 54 60 66 78 90 102
150
38 42 46 50 54 60 66 78 90 102
160,
170,
190,
200, 44 48 52 56 60 66 72 84 96 108
180
240,260,280,
220
Примечание:
знаком * отмечены болты с резьбой по всей длине стержня.
300
Для консервации контактных поверхностей стальных деталей
следует применять фрикционный грунт ВЖС 83-02-87 по ТУ. Для
нанесения на опорные поверхности шайб методом плазменного
53
54.
54напыления антифрикционного покрытия следует применять в
качестве материала подложки интерметаллид ПН851015 по ТУ14-1-3282-81, для несущей структуры - оловянистую бронзу
БРОФ10-8 по ГОСТ, для рабочего тела - припой ПОС-60 по ГОСТ.
Примечание: Приведенные данные действительны при сроке
хранения несобранных конструкций до 1 года.
6.2. Конструктивные требования к соединениям
В
конструкциях
соединений
должна
быть
обеспечена
возможность свободной постановки болтов, закручивания гаек и
плотного
стягивания
постановки
с
пакета
болтами
применением
во
всех
местах
динамометрических
ключей
их
и
гайковертов.
Номинальные
диаметры
круглых
и
ширина
овальных
отверстий в элементах для пропуска высокопрочных болтов
принимаются по табл.6.3.
Таблица 6.3.
Группа
Номинальный диаметр болта в мм.
16 18 20 22 24 27 30 36 42 48
соединений
Определяющи 17 19 21 23 25 28 32 37 44 50
х геометрию
Не
20
23
25
28
30
33
36
40
45
52
определяющи
Длины овальных
х геометрию
отверстий
в
элементах
для
пропуска
высокопрочных болтов назначают по результатам вычисления
максимальных абсолютных смещений соединяемых деталей для
каждого ФПС по результатам предварительных расчетов при
обеспечении
несоприкосновения
болтов
о
края
овальных
отверстий, и назначают на 5 мм больше для каждого возможного
направления смещения.
54
55.
55ФПС следует проектировать возможно более компактными.
Овальные отверстия одной детали пакета ФПС могут быть не
сонаправлены.
Размещение болтов в овальных отверстиях при сборке ФПС
устанавливают
с
учетом
назначения
ФПС
и
направления
смещений соединяемых элементов.
При необходимости в пределах одного овального отверстия
может быть размещено более одного болта.
Все
контактные
поверхности
деталей
ФПС,
являющиеся
внутренними для ФПС, должны быть обработаны грунтовкой
ВЖС 83-02-87 после дробеструйной (пескоструйной) очистки.
Не допускается осуществлять подготовку тех поверхностей
деталей ФПС, которые являются внешними поверхностями ФПС.
Диаметр болтов ФПС следует принимать не менее 0,4 от
толщины соединяемых пакета соединяемых деталей.
Во всех случаях несущая способность основных элементов
конструкции, включающей ФПС, должна быть не менее чем на
25%
больше
несущей
способности
ФПС
на
фрикционно-
неподвижной стадии работы ФПС.
Минимально
допустимое
расстояние
от
края
овального
отверстия до края детали должно составлять:
- вдоль направления смещения >= 50 мм.
- поперек направления смещения >= 100 мм.
В соединениях прокатных профилей с непараллельными
поверхностями
полок
или
при
наличии
непараллельности
наружных плоскостей ФПС должны применяться клиновидные
шайбы, предотвращающие перекос гаек и деформацию резьбы.
Конструкции
ФПС
и
конструкции,
обеспечивающие
соединение ФПС с основными элементами сооружения, должны
55
56.
56допускать
возможность
ведения
последовательного
не
нарушающего связности сооружения ремонта ФПС.
6.3. Подготовка контактных поверхностей элементов
и методы контроля.
Рабочие контактные поверхности элементов и деталей ФПС
должны быть подготовлены посредством либо пескоструйной
очистки
в
соответствии
с
указаниями
ВСН
163-76,
либо
дробеструйной очистки в соответствии с указаниями.
Перед обработкой с контактных поверхностей должны быть
удалены заусенцы, а также другие дефекты, препятствующие
плотному прилеганию элементов и деталей ФПС.
Очистка должна производиться в очистных камерах или под
навесом,
или
на
открытой
площадке
при
отсутствии
атмосферных осадков.
Шероховатость поверхности очищенного металла должна
находиться в пределах 25-50 мкм.
На очищенной поверхности не должно быть пятен масел,
воды и других загрязнений.
Очищенные
контактные
соответствовать
первой
поверхности
степени
удаления
должны
окислов
и
обезжиривания по ГОСТ 9022-74.
Оценка
шероховатости
контактных
поверхностей
производится визуально сравнением с эталоном или другими
апробированными способами оценки шероховатости.
Контроль степени очистки может осуществляться внешним
осмотром поверхности при помощи лупы с увеличением не менее
56
57.
576-ти кратного. Окалина, ржавчина и другие загрязнения на
очищенной поверхности при этом не должны быть обнаружены.
Контроль
степени
обезжиривания
осуществляется
следующим образом: на очищенную поверхность наносят 2-3
капли бензина и выдерживают не менее 15 секунд. К этому
участку поверхности прижимают кусок чистой фильтровальной
бумаги и держат до полного впитывания бензина. На другой
кусок фильтровальной бумаги наносят 2-3 капли бензина. Оба
куска выдерживают до полного испарения бензина. При дневном
освещении
сравнивают
фильтровальной
внешний
бумаги.
Оценку
вид
степени
обоих
кусков
обезжиривания
определяют по наличию или отсутствию масляного пятна на
фильтровальной бумаге.
Длительность
перерыва
между
пескоструйной
очисткой
поверхности и ее консервацией не должна превышать 3 часов.
Загрязнения, обнаруженные на очищенных поверхностях, перед
нанесением консервирующей грунтовки ВЖС 83-02-87 должны
быть
удалены
жидким
калиевым
стеклом
или
повторной
очисткой. Результаты проверки качества очистки заносят в
журнал.
6.4. Приготовление и нанесение протекторной
грунтовки ВЖС 83-02-87. Требования к
загрунтованной поверхности. Методы контроля
Протекторная грунтовка ВЖС 83-02-87 представляет собой
двуупаковочный
лакокрасочный
материал,
состоящий
из
алюмоцинкового сплава в виде пигментной пасты, взятой в
количестве 66,7% по весу, и связующего в виде жидкого
57
58.
58калиевого стекла плотностью 1,25, взятого в количестве 33,3%
по весу.
Каждая
партия
документации
поступившие
материалов
на
должна
соответствие
без
ТУ.
быть
проверена
Применять
документации
по
материалы,
завода-изготовителя,
запрещается.
Перед смешиванием составляющих протекторную грунтовку
ингредиентов
следует
довести
жидкое
калиевое
стекло
до
необходимой плотности 1,25 добавлением воды.
Для приготовления грунтовки ВЖС 83-02-87 пигментная
часть и связующее тщательно перемешиваются и доводятся до
рабочей вязкости 17-19 сек. при 18-20°С добавлением воды.
Рабочая вязкость грунтовки определяется вискозиметром ВЗ4 (ГОСТ 9070-59) по методике ГОСТ 17537-72.
Перед
и
во
время
нанесения
следует
перемешивать
приготовленную грунтовку до полного поднятия осадка.
Грунтовка
ВЖС
83-02-87
сохраняет
малярные
свойства
(жизнеспособность) в течение 48 часов.
Грунтовка ВЖС 83-02-87 наносится под навесом или в
помещении. При отсутствии атмосферных осадков нанесение
грунтовки можно производить на открытых площадках.
Температура воздуха при произведении работ по нанесению
грунтовки ВЖС 83-02-87 должна быть не ниже +5°С.
Грунтовка
ВЖС
83-02-87
может
наноситься
методами
пневматического распыления, окраски кистью, окраски терками.
Предпочтение следует отдавать пневматическому распылению.
Грунтовка ВЖС 83-02-87 наносится за два раза по взаимно
перпендикулярным
направлениям
с
промежуточной
сушкой
между слоями не менее 2 часов при температуре +18-20°С.
58
59.
59Наносить грунтовку следует равномерным сплошным слоем,
добиваясь окончательной толщины нанесенного покрытия 90110 мкм. Время нанесения покрытия при естественной сушке при
температуре воздуха 18-20 С составляет 24 часа с момента
нанесения последнего слоя.
Сушка загрунтованных элементов и деталей во избежание
попадания
атмосферных
осадков
и
других
загрязнений
на
невысохшую поверхность должна проводится под навесом.
Потеки, пузыри, морщины, сорность, не прокрашенные места
и другие дефекты не допускаются. Высохшая грунтовка должна
иметь серый матовый цвет, хорошее сцепление (адгезию) с
металлом и не должна давать отлипа.
Контроль
толщины
покрытия
осуществляется
магнитным
толщиномером ИТП-1.
Адгезия определяется методом решетки в соответствии с
ГОСТ
15140-69
на
контрольных
образцах,
окрашенных
по
принятой технологии одновременно с элементами и деталями
конструкций.
Результаты
проверки
качества
защитного
покрытия
заносятся в Журнал контроля качества подготовки контактных
поверхностей ФПС.
6.4.1 Основные требования по технике безопасности
при работе
с грунтовкой ВЖС 83-02-87
Для обеспечения условий труда необходимо соблюдать:
59
60.
60"Санитарные
применением
правила
при
ручных
окрасочных
распылителей"
работах
с
(Министерство
здравоохранения СССР, № 991-72)
"Инструкцию по санитарному содержанию помещений и
оборудования производственных предприятий" (Министерство
здравоохранения СССР, 1967 г.).
При
пневматическом
увеличения
методе
распыления,
туманообразования
и
расхода
во
избежание
лакокрасочного
материала, должен строго соблюдаться режим окраски. Окраску
следует производить в респираторе и защитных очках. Во время
окрашивания
в
располагаться
таким
материала
имела
закрытых
помещениях
образом,
чтобы
направление
струя
маляр
должен
лакокрасочного
преимущественно
в
сторону
воздухозаборного отверстия вытяжного зонта. При работе на
открытых площадках маляр должен расположить окрашиваемые
изделия так, чтобы ветер не относил распыляемый материал в
его сторону и в сторону работающих вблизи людей.
Воздушная магистраль и окрасочная аппаратура должны
быть оборудованы редукторами давления и манометрами. Перед
началом
работы
маляр
должен
проверить
герметичность
шлангов, исправность окрасочной аппаратуры и инструмента, а
также
надежность
присоединения
краскораспределителю
и
воздушных
шлангов
воздушной
к
сети.
Краскораспределители, кисти и терки в конце рабочей смены
необходимо
тщательно
очищать
и
промывать
от
остатков
грунтовки.
На каждом бидоне, банке и другой таре с пигментной частью
и связующим должна быть наклейка или бирка с точным
60
61.
61названием и обозначением этих материалов. Тара должна быть
исправной с плотно закрывающейся крышкой.
При приготовлении и нанесении грунтовки ВЖС 83-02-87
нужно соблюдать осторожность и не допускать ее попадания на
слизистые оболочки глаз и дыхательных путей.
Рабочие
и
ИТР,
работающие
на
участке
консервации,
допускаются к работе только после ознакомления с настоящими
рекомендациями, проведения инструктажа и проверки знаний по
технике
безопасности.
На
участке
консервации
и
в
краскозаготовительном помещении не разрешается работать без
спецодежды.
Категорически запрещается прием пищи во время работы.
При попадании составных частей грунтовки или самой грунтовки
на слизистые оболочки глаз или дыхательных путей необходимо
обильно промыть загрязненные места.
61
62.
626.4.2 Транспортировка и хранение элементов и
деталей, законсервированных грунтовкой
ВЖС 83-02-87
Укладывать,
законсервированные
исключить
хранить
и
элементы
возможность
и
транспортировать
детали
нужно
механического
так, чтобы
повреждения
и
загрязнения законсервированных поверхностей.
Собирать можно только те элементы и детали, у которых
защитное
покрытие
высохло.
контактных
Высохшее
защитное
поверхностей
полностью
покрытие
контактных
поверхностей не должно иметь загрязнений, масляных пятен и
механических повреждений.
При наличии загрязнений и масляных пятен контактные
поверхности
должны
быть
обезжирены.
Обезжиривание
контактных поверхностей, законсервированных ВЖС 83-02-87,
можно
производить
водным
раствором
жидкого
калиевого
стекла с последующей промывкой водой и просушиванием.
Места механических повреждений после обезжиривания должны
быть подконсервированы.
6.5. Подготовка и нанесение антифрикционного
покрытия на опорные поверхности шайб
Производится очистка только одной опорной поверхности
шайб в дробеструйной камере каленой дробью крупностью не
более 0,1 мм. На отдробеструенную поверхность шайб методом
плазменного напыления наносится подложка из интерметаллида
ПН851015 толщиной . …..м. На подложку из интерметаллида
62
63.
63ПН851015 методом плазменного напыления наносится несущий
слой
оловянистой
бронзы
БРОФ10-8.
На
несущий
слой
оловянистой бронзы БРОФ10-8 наносится способом лужения
припой ПОС-60 до полного покрытия несущего слоя бронзы.
6.6. Сборка ФПС
Сборка
ФПС
фрикционным
проводится
покрытием
с
использованием
одной
из
шайб
поверхностей,
с
при
постановке болтов следует располагать шайбы обработанными
поверхностями внутрь ФПС.
Запрещается
деталей
ФПС.
очищать
внешние
Рекомендуется
поверхности
использование
внешних
неочищенных
внешних поверхностей внешних деталей ФПС.
Каждый болт должен иметь две шайбы (одну под головкой,
другую под гайкой). Болты и гайки должны быть очищены от
консервирующей смазки, грязи и ржавчины, например, промыты
керосином и высушены.
Резьба болтов должна быть прогнана путем провертывания
гайки от руки на всю длину резьбы. Перед навинчиванием гайки
ее резьба должна быть покрыта легким слоем консистентной
смазки.
Рекомендуется следующий порядок сборки:
совмещают отверстия в деталях и фиксируют их взаимное
положение;
устанавливают
гайковертами
на
болты
90%
от
и
осуществляют
проектного
их
усилия.
натяжение
При
сборке
многоболтового ФПС установку болтов рекомендуется начать с
болта находящегося в центре тяжести поля установки болтов, и
63
64.
64продолжать установку от центра к границам поля установки
болтов;
после
проверки
плотности
стягивания
ФПС
производят
герметизацию ФПС;
болты затягиваются до нормативных усилий натяжения
динамометрическим ключом.
64



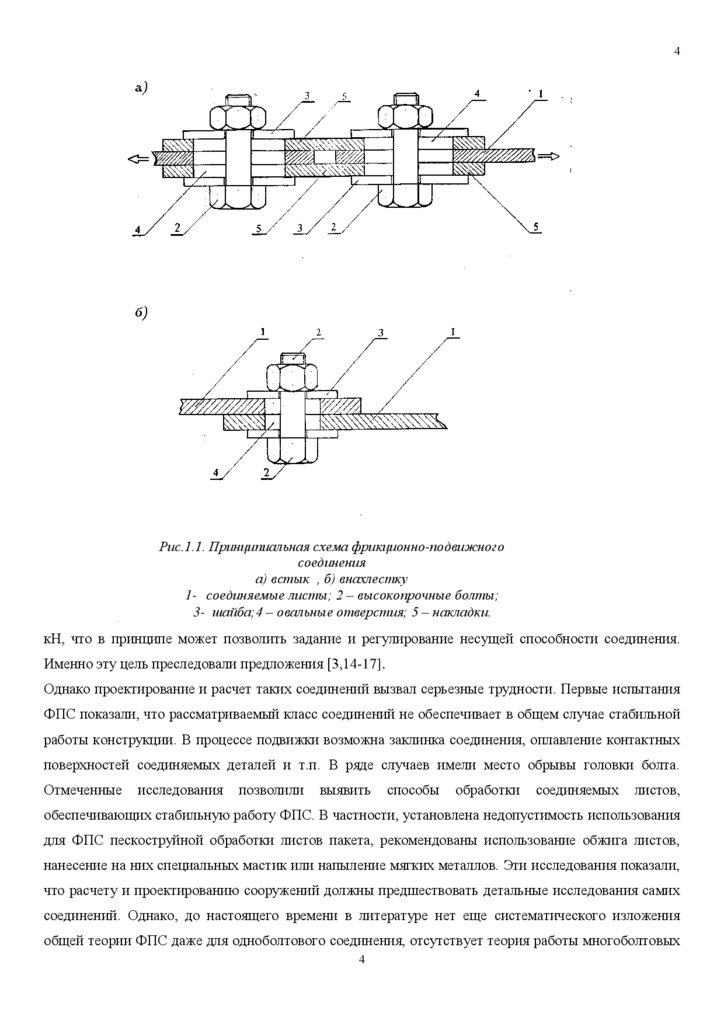




















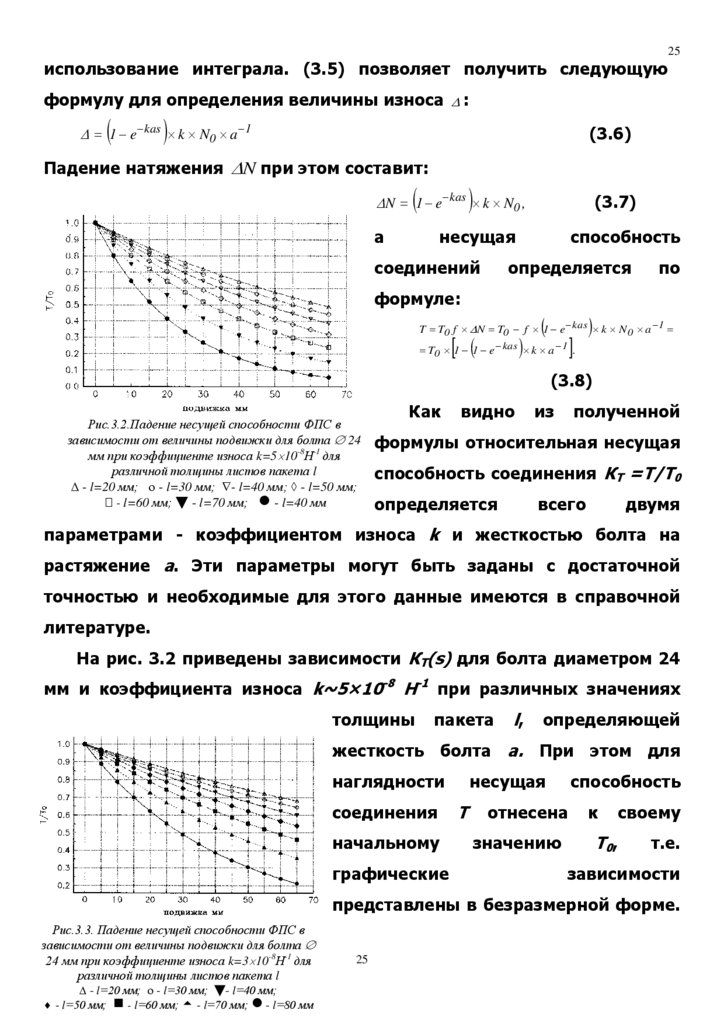



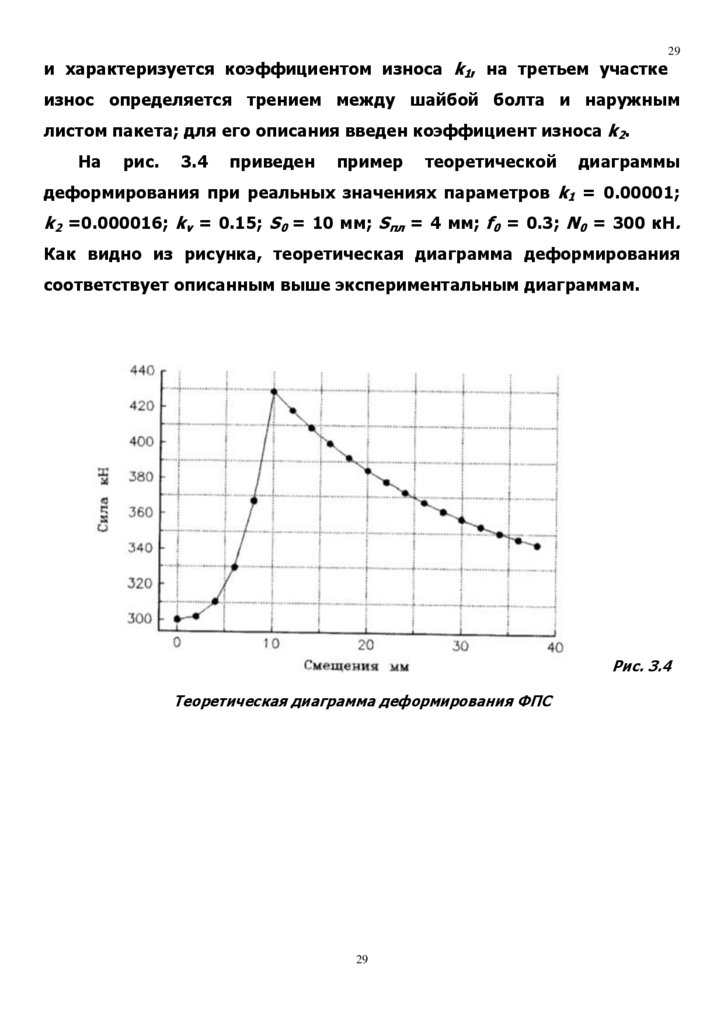



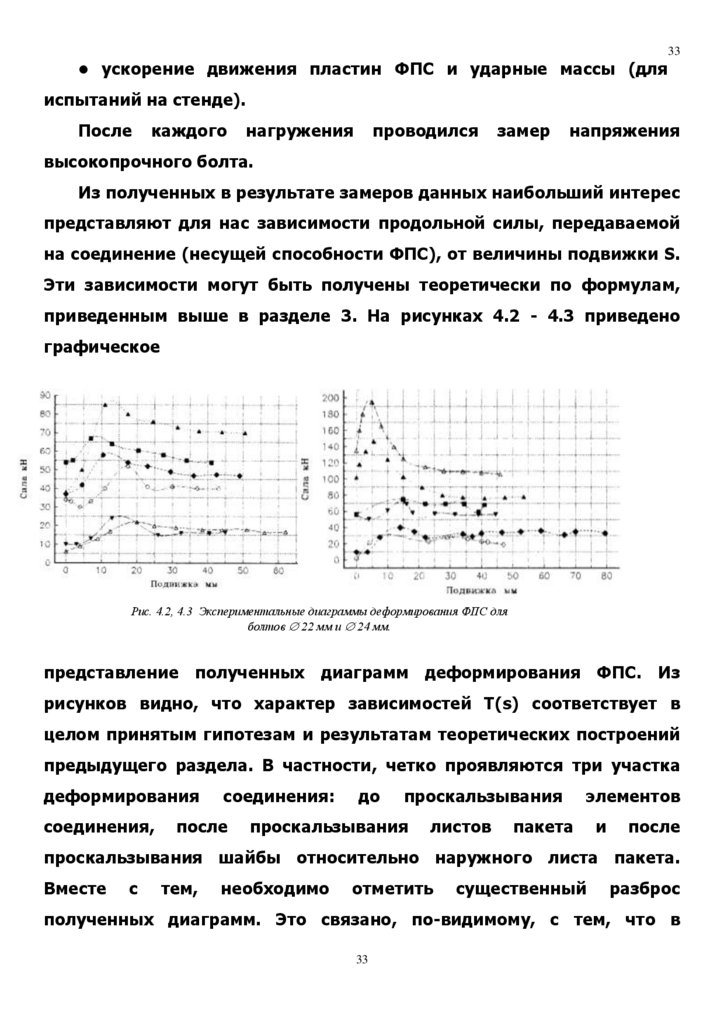

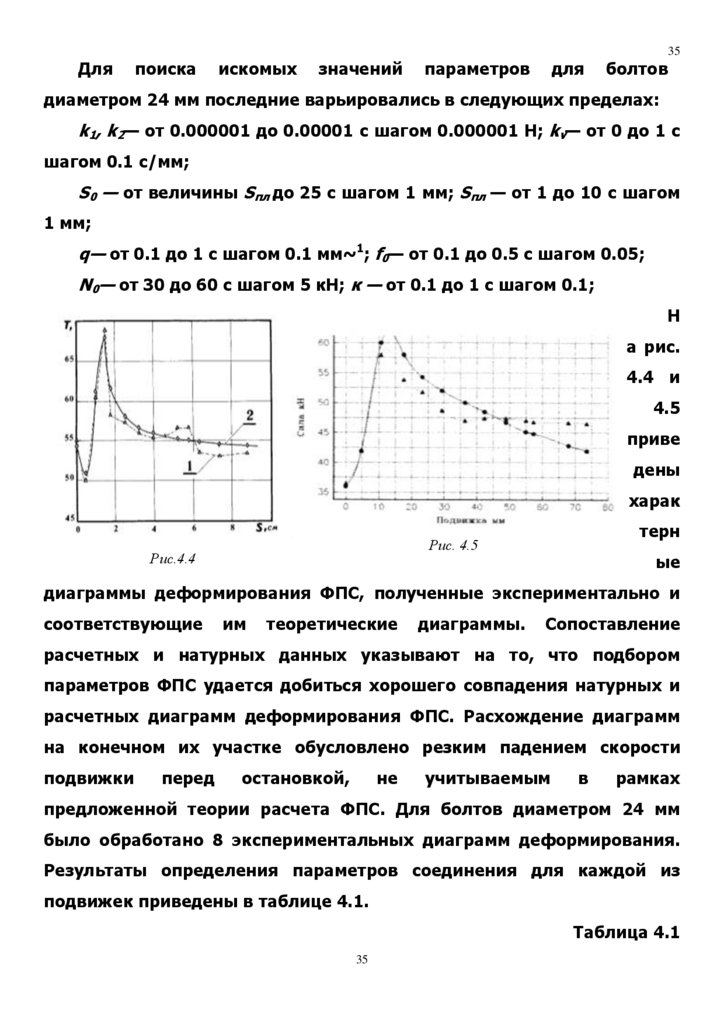








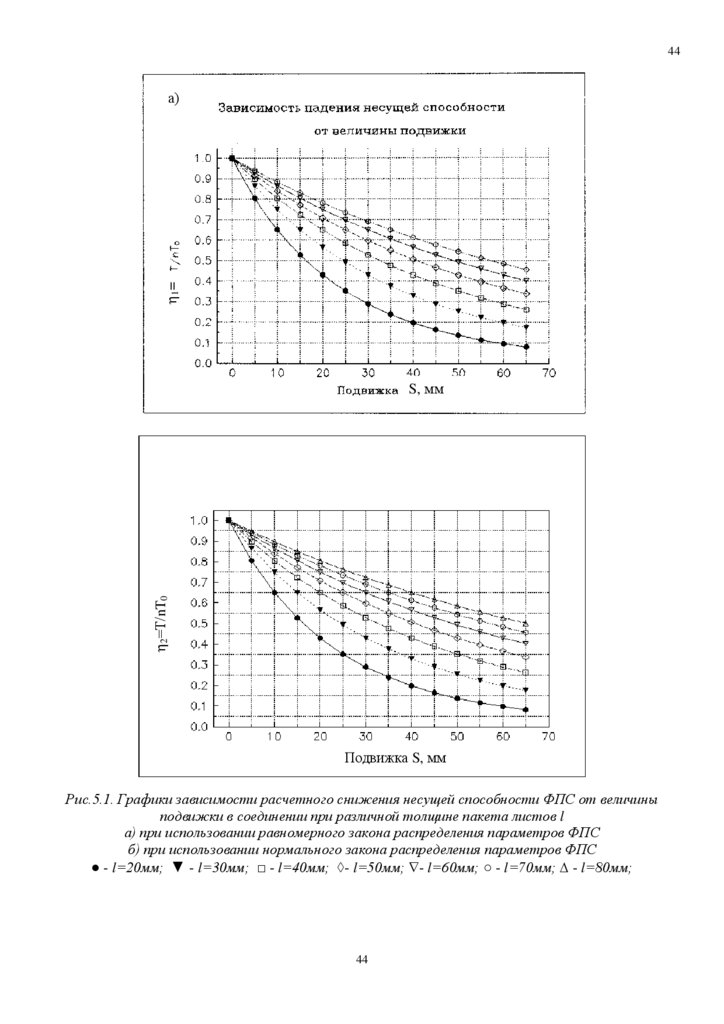
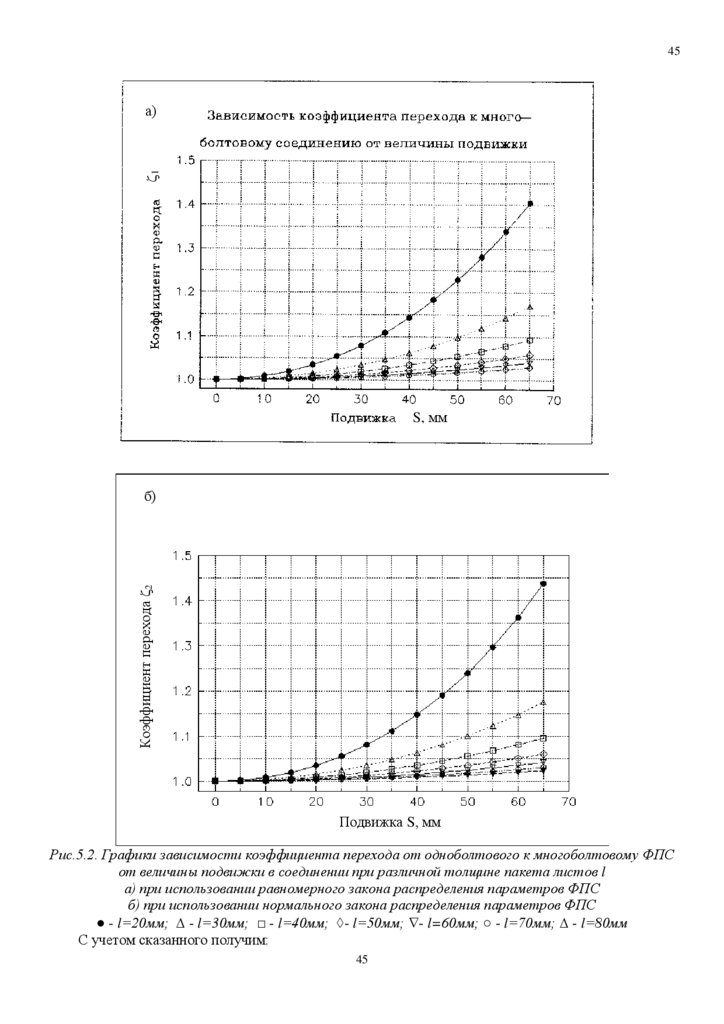
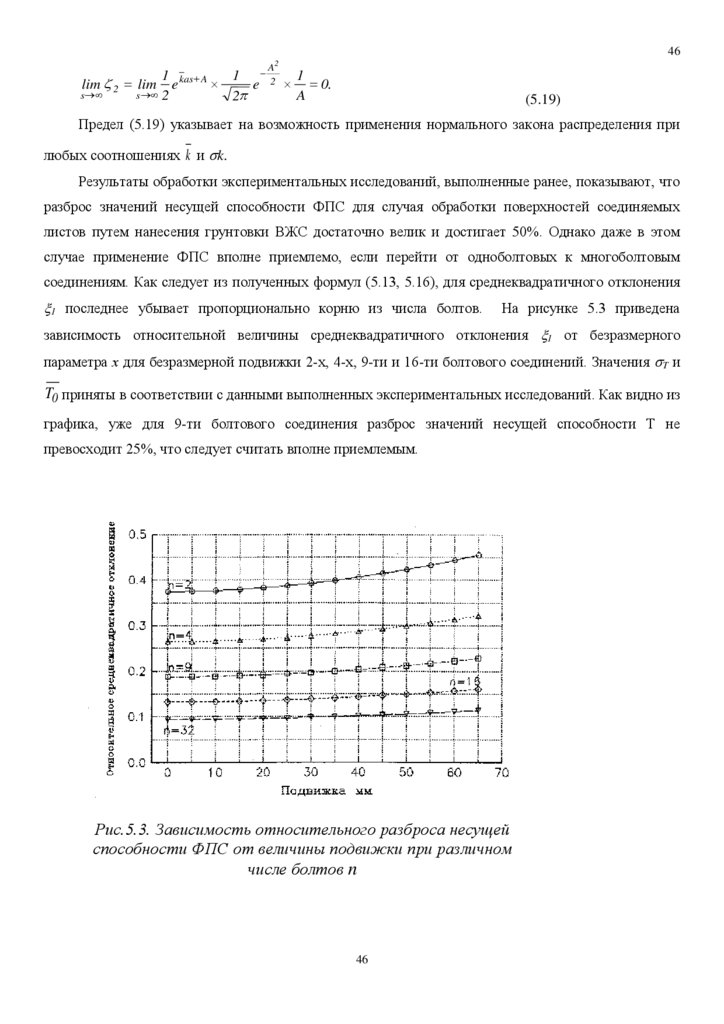




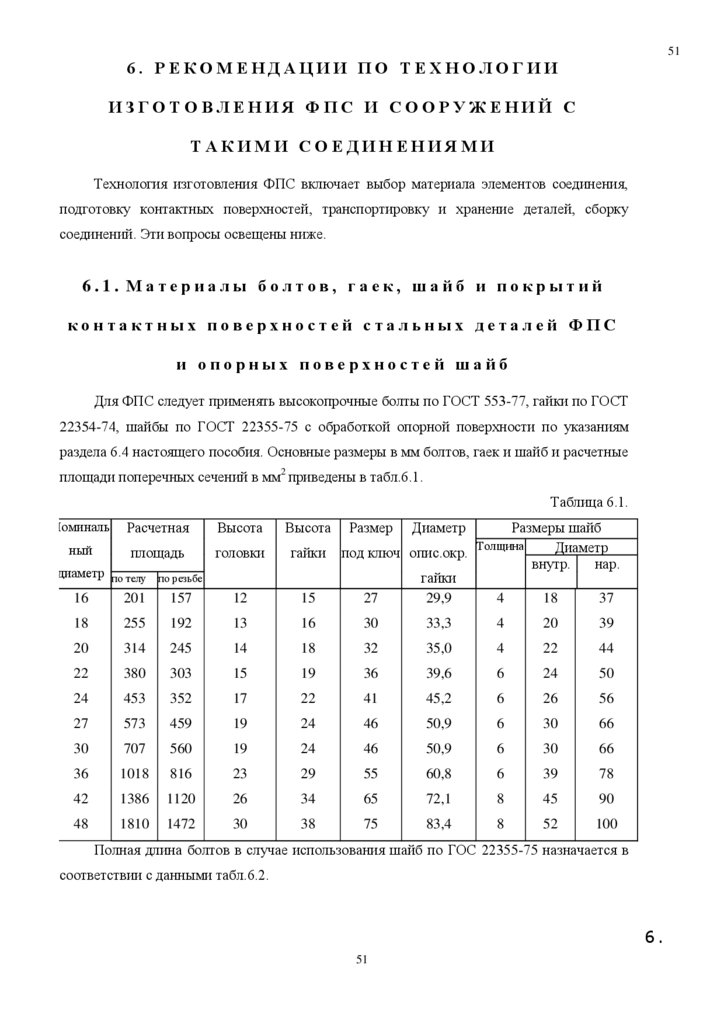
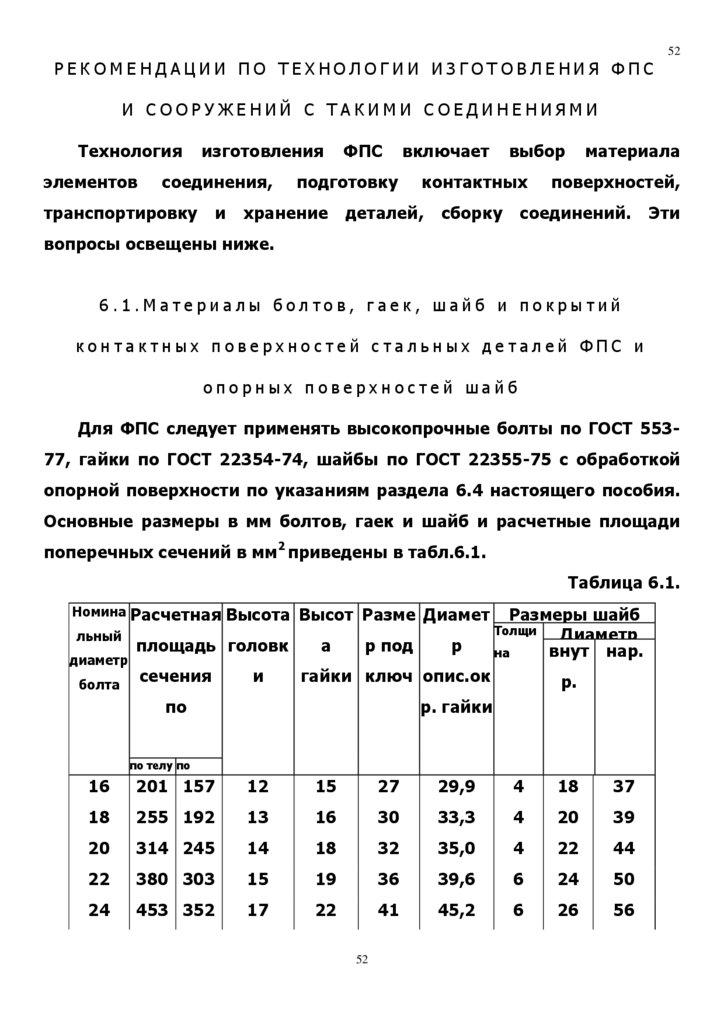
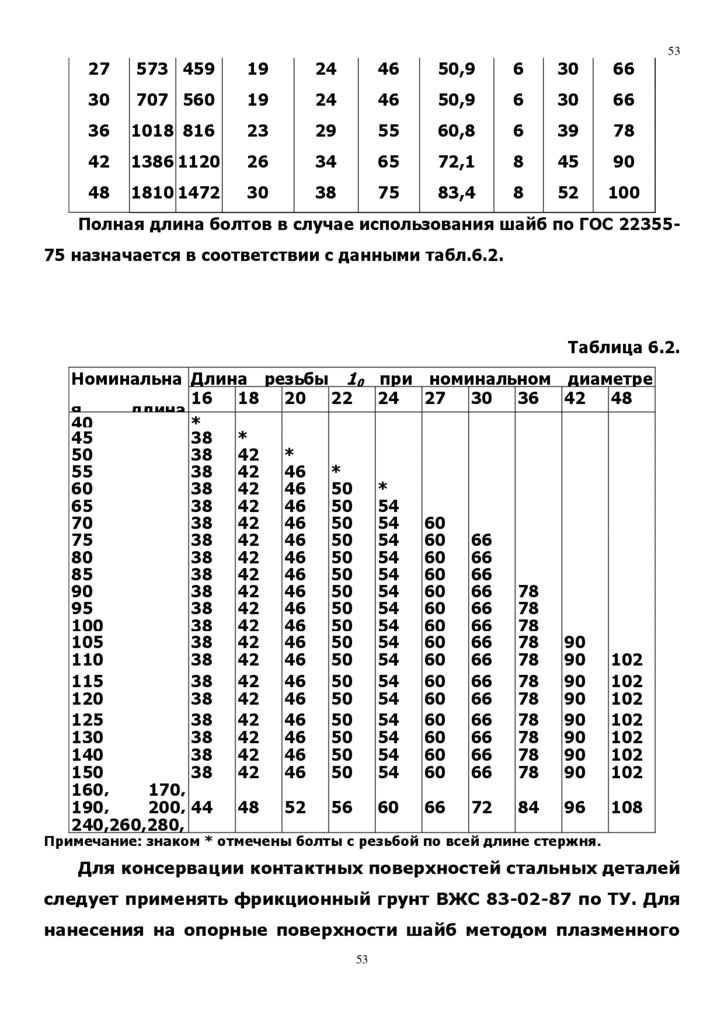











 Construction
Construction








