Непрерывность функции одной переменной. Точки разрыва функции и их классификация

1. НЕПРЕРЫВНОСТЬ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ
КЛАССИФИКАЦИЯ

2. Определение непрерывности функции

Функция y = f (x) называется непрерывной в точке x0 ,
если выполняются условия:
1) Функция определена в точке x0 ;
2) Односторонние пределы функции в точке x0 равны
æ
ö
lim
f
(
x
)
=
lim
f
(
x
)
;
между собой: ç x ® x -0
÷
x® x +0
è
0
0
ø
3) Односторонние пределы равны значению функции
в точке x0æ:
ö
f ( x) = lim f ( x) = lim f ( x) = f ( x0 ) ÷ .
ç x ®lim
x ® x0 + 0
x ® x0
è x0 -0
ø

3. Свойства непрерывных функций

1.
2.
3.
Если даны две непрерывные функции в точке x0,
то их сумма, разность и произведение является
непрерывной функцией.
Основные элементарные функции непрерывны в
своей области определения;
Функция является непрерывной на интервале,
если она непрерывна в каждой точке этого
интервала.

4. Определение точки разрыва функции

Если в точке x0 нарушается хотя бы одно
условие определения непрерывности в
точке x0 , то такая точка называется
точкой разрыва функции y = f (x).

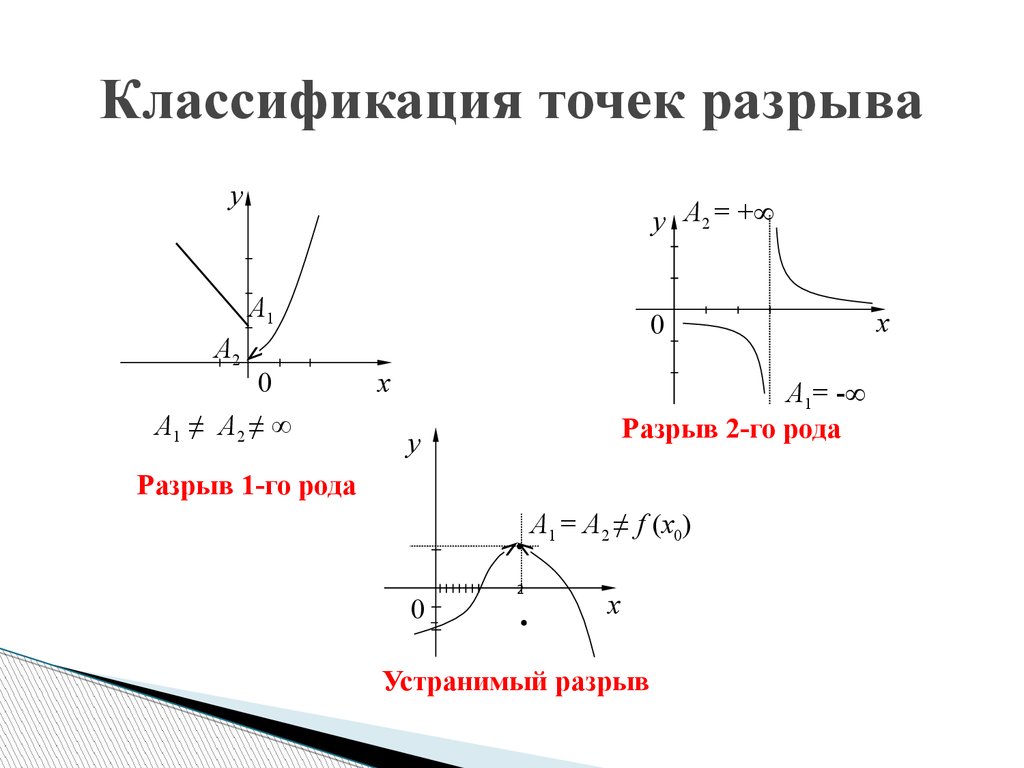
5. Классификация точек разрыва

y
y A2 = +
A1
A2
0
A1 ≠ A2 ≠ ∞
0
x
A1= -
Разрыв 2-го рода
y
Разрыв 1-го рода
A1 = A2 ≠ f (x0)
0–
2
x
Устранимый разрыв
x

6. Характеристика точек разрыва

Разрыв 1-го рода: Если в точке существует левосторонний и
правосторонний пределы, но при этом они конечны и
различны, а значение функции в этой точке не определено.
Разрыв 2-го рода: Если в точке существует левосторонний и
правосторонний пределы, но при этом они один или оба
бесконечны (иногда один из односторонних пределов может
не существовать), а значение функции в этой точке не
определено.
Устранимый разрыв. Если в точке существует левосторонний
и правосторонний пределы, но при этом они конечны и
одинаковы, но не равны значению функции в этой точке.

7. Спасибо за внимание!!! =)