Similar presentations:
Теория Бора для атома водорода
1.
Военно-космическая академия имени А. Ф. МожайскогоКафедра №112 (Физики)
Раздел 5. Основы квантовой физики
Тема 31: Физика и свойства
атомов и молекул
Лекция 1: Теория Бора для атома
водорода
2.
Цель лекции – познакомиться физическими свойствами истроением атома, выяснить природу линейчатых спектров
излучения.
Вопросы лекции:
1. Линейчатый спектр атома
водорода
2. Ядерная модель атома Резерфорда.
Постулаты Бора
3. Теория Бора для водородоподобных
систем
Литература:
БЭУ п. 31.1 – 31.4; Доп. [1, стр. 390-398]; [2, стр. 335-344].
Техническое обеспечение:
Комплект мультимедийных средств обучения.
База данных анимаций физических процессов.
3.
ВведениеН
Газ при
излучать.
нагревании
начинает
Но излучение происходит только на
определенных частотах, своих для
каждого газа!
Атомы каждого химического элемента
имеют
строго
определенный
индивидуальный линейчатый спектр.
Почему частоты излучения атомами
имеют дискретные значения?
4.
Вопрос №1Линейчатый спектр атомов водорода
5.
Имеем разреженный газ, состоящий из атомов H.Нагреваем газ – начинается излучение.
Спектр излучения (испускания) водорода
Н
700 нм
656 нм
600 нм
500 нм
485 нм
400 нм
434 нм
410 нм
6.
700 нмН
656 нм
Спектр излучения
(испускания) водорода
600 нм
500 нм
485 нм
400 нм
Выводы:
434 нм
410 нм
1. Атомы имеют дискретный спектр излучения.
2. По набору линий спектра испускания можно
определить химический элемент (спектральный анализ).
7.
Спектр поглощения водородаИмеем разреженный атомарный газ в холодном
состоянии. Свечения нет.
Пропустим сквозь газ свет с непрерывным спектром.
На выходе в непрерывном спектре увидим узкие
черные полосы.
Для перевода атомов газа в возбужденное состояние
годятся строго определенные длины волн для данного
газа. Эти длины волн газ и «забирает себе» из
проходящего света.
8.
9.
Темные линии в спектре поглощения газасоответствуют ярким линиям его спектра испускания.
Вывод: при прямом и обратном переходах между
дискретными энергетическими состояниями атомы
излучают и поглощают ЭМВ одинаковой частоты.
Закономерности в спектре излучения атома водорода
Формула И. Бальмера (1885 г.)
2
n
0 2 ,
n 4
0 364,613 нм,
где
(1)
n 3,4, ,11.
Впервые показана особая роль целых чисел
спектральных закономерностях.
в
10.
Формула Бальмера (1885 г.)2
n
0 2 ,
n 4
0 364,613 нм,
где
(1)
n 3,4, ,11.
Впервые показана особая роль целых
чисел в спектральных закономерностях.
11.
Формула Ридберга1 1
R 2 2 ,
2 n
R 3,29 1015 c 1
nБ
где
n 3,4, .
(2)
– постоянная Ридберга.
Формула Ридберга для длины волны:
4c n 4
(3)
n 2 ,
R n
n 3,4, .
2
12.
Обобщенная формула Бальмера – Ридберга(для всех линий)
1 1
n R 2 2 ,
k n
где
n k 1, k 2,
k 1,2,3,
.
(4)
– целое число.
Выводы:
1. Спектр излучения газа – «паспорт» химического
элемента (спектральный анализ – метод исследования
вещества по его спектру).
2. Наличие спектра свидетельствует о том, что атом – не
есть неделимая частица, он имеет собственную структуру.
3. Уникальность атомных спектров свидетельствует о
том, что атомы разных элементов устроены по-разному.
13.
Вопрос №2Ядерная модель атома Резерфорда
14.
Модель Томсона (1898 г.)Атом – шар диаметром 10 10 м.
Положительный заряд равномерно распределен по шару.
Внутри шара находятся электроны («булочка с изюмом»).
Атом электрически нейтрален.
Излучение вызвано колебаниями электронов около
положения равновесия.
Но почему тогда спектр линейчатый?
15.
Опыт Резерфорда (1912 г.)Почему ???
Что-то есть внутри атома
такое, что стоит на пути
частиц.
d 0,5 мкм
Суть эксперимента – бомбардировка атома
высокоэнергетичными α – частицами.
Результат – небольшая часть α – частиц (одна из нескольких
тысяч) отклонялась на угол больший чем 90 градусов.
16.
Опыт Резерфорда (1912 г.)Суть эксперимента – бомбардировка атома
α-частицами.
Упругое
столкновение
Отклонение
силой Кулона
Au
α-частица имеет положительный заряд, равный 2е и
4
массу, в 8000 раз большую, чем масса электрона ( 2 – 2
протона + 2 нейтрона).
Результат опыта – помимо рассеяния небольшая часть
α-частиц отклонялась на угол свыше 90 градусов.
Причина - что-то есть такое внутри атома, что стоит
на пути α-частиц.
17.
Планетарная модель атома18.
Планетарная модель атома19.
Планетарная модель атомаМежду ядром и электронами
действуют
силы
кулоновского
притяжения.
Практически вся масса атома сосредоточена в
небольшом в ядре !!!
Если бы атом имел размер 500 м, то размер ядра был бы 5 мм.
Рассеяние α-частиц – есть результат их отклонения от
ядра силой Кулона.
Отражение α-частиц – результат их упругого
столкновения с ядром.
20.
Основной недостаток планетарной модели атома –невозможность объяснить линейчатый спектр и
устойчивость атома.
На электрон, вращающийся вокруг ядра атома
водорода, действует нормальное (центростремительное)
ускорение an 2 rБ .
e
e
2
, k
.
Сила Кулона k 2 m
rБ
rБ
mrБ
2
2
2
Всякий ускоренно движущийся заряд излучает ЭМВ,
т.е. теряет энергию. Полная энергия электрона
!
e2
e2
e2
m 2
e2
k
k k
W WК WП
.
k
2rБ
rБ
2rБ
2
rБ
21.
2e2
2
e
2
, k
.
Сила Кулона k 2 m
rБ
rБ
mrБ
Всякий ускоренно движущийся заряд излучает ЭМВ,
т.е. теряет энергию. Полная энергия электрона
!
e
e
e
m
e
k
k k
W WК WП
.
k
2rБ
rБ
2rБ
2
rБ
2
Если
W , то W ,
2
2
2
2
rБ .
В итоге электрон должен упасть на атом (через t 10 10 c ).
Атом прекратит свое существование.
Вывод: внутри атомов действуют другие законы –
законы квантовой физики.
22.
Постулаты БораПервый постулат
(постулат стационарных состояний)
Существуют стационарные состояния
атома, находясь в которых он не излучает
энергию.
Каждое из этих состояний характеризуется
определенным уровнем энергии:
Wn ,
n 1, 2,3,
.
23.
Первый постулат (постулат стационарных состояний)Существуют стационарные состояния атома,
находясь в которых он не излучает энергию.
Каждое из этих состояний характеризуется
определенным уровнем энергии: Wn , n 1, 2,3, .
Второй постулат
(правило квантования Бора)
В стационарном состоянии атома электрон,
двигаясь по круговой орбите, должен иметь
квантованные значения момента импульса,
кратные постоянной Планка:
me n rn n ,
n 1, 2,3,
.
(5)
24.
Второй постулат (правило квантования Бора)В стационарном состоянии атома электрон,
двигаясь по круговой орбите, должен иметь
квантованные значения момента импульса, кратные
постоянной Планка:
(5)
me n rn n , n 1, 2,3, .
Третий постулат
(правило частот)
При переходе электрона из одного
стационарного
состояния
в
другое
испускается или поглощается один фотон:
me n rn n , n 1,2,3, .
(6)
25.
Третий постулат (правило частот)При переходе электрона из одного стационарного
состояния в другое испускается или поглощается
(6)
h Wn Wk .
один фотон:
Пример: излучение фотона при
переходе электрона с уровня W3
на уровень W1 .
e
W1 W
2
W3
h Wn Wk .
!!! Атом может излучать волны только
тех частот, которые соответствуют разностям значений
энергии разрешенных уровней: Wn Wk .
Это объясняет линейчатый спектр излучения, полученный
опытным путем.
26.
Вопрос №3Теория Бора для водородоподобных
систем
27.
Модель атома водородаn
e
Ze
Уравнение движения электрона:
Выразим
Ze
Fк
.
ац
. ац
2
rn 4 0me rn
me
2
2
n
2
Z
e
2
.
Ze
4
m
r
Fк
.
0
e
n
2
4 0 rn
2
n
С учетом (5):
2
2
nh
me n rn n , 2 2 2 .
4 me rn
2
n
2
2
2
nh
Ze
.
2 2 2
4 me rn 4 0me rn
(7)
(8)
28.
2С учетом (5):
2
nh
me n rn n , 2 2 2 .
4 me rn
2 2
2
nh
Ze
.
2 2 2
4 me rn 4 0me rn
2
n
0h
rn n
.
2
me Ze
2
2
(9)
Для атома водорода (Z=1) (первый Боровский радиус):
r1 0,528 10
10
м.
29.
Уровни энергий в атоме водорода (Z = 1)(энергетические уровни)
2
Ze
К
П
Полная энергия электрона: Wn Wn Wn
.
8
r
0
n
2
2
Ze
me n
.
W
8 0 rn
2
К
n
2
Ze
П
Wn
.
4 0 rn
(9)
С учетом (9):
2 4
1 me Z e
Wn 2
.
2 2
n 8 0 h
Минимальной энергией атом обладает при n 1
– основное (нормальное) состояние атома:
W1 13, 6 эВ.
(10)
30.
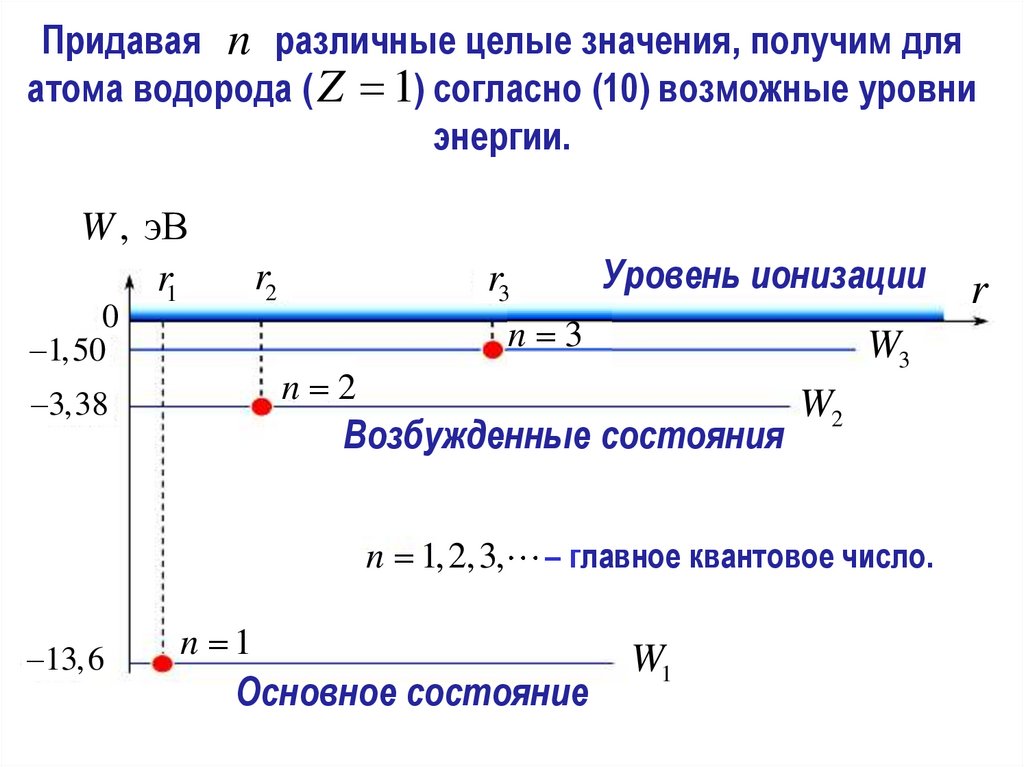
Придавая n различные целые значения, получим дляатома водорода ( Z 1) согласно (10) возможные уровни
энергии.
W , эВ
r1
r2
0
1,50
n 3
W3
n 2
3,38
Возбужденные состояния
n 1, 2,3,
13,6
Уровень ионизации
r3
W2
– главное квантовое число.
n 1
Основное состояние
W1
r
31.
(10)Спектральные серии
me 1
1
h Wk Wn 2 2 2 2 .
8h 0 k
n
4
me 4 1
1
2 , n k 1, k 2 ,
3 2
2
8h 0 k
n
R 3, 29 10
15
с
1
.
постоянная Ридберга.
Обобщенная формула Бальмера
1
1
R 2 2 , n k 1, k 2 ,
n
k
. (11)
Выражение (11) соответствует эмпирической формуле (2).
32.
Физическая трактовка серийспектральных линий для атома водорода,
наблюдаемых экспериментально
33.
Причины возбуждения атомаводорода:
• нагревание;
• электроразряд;
• поглощение света.
1. Атом водорода поглощает
определённые порции — кванты
энергии, соответствующие
разности энергетических уровней
электронов.
2. Обратный переход электрона
сопровождается выделением
точно такой же порции энергии.
34.
Для атома H серия Лаймана: переход электрона на первую(основную) орбиту с любой другой орбиты, начиная со второй,
(атом переходит из возбужденного состояния в основное).
Серию Лаймана получим,
подставляя в (11)
k 1, n 2,3,
.
1
1
R 2 2 .
n
k
Вторая серия – серия
Бальмера соответствует
переходу электрона на
вторую орбиту с любой
более высокой орбиты.
Самостоятельно
[1], стр. 396.
ЭУ п. 31.4
35.
Орбитальнаятрактовка
серий
спектральных
линий атома
водорода.
36.
ЗаключениеТеория Бора объясняет
наличие линейчатых спектров.
1. Каждая спектральная линия – результат перехода
электрона из одного стационарного состояния в другое.
2. Разность энергий между энергетическими уровнями
определяет частоту излучения (положение линии в
спектре).
h Wk Wn
me 4 1
1
1
1
2 R 2 2 .
3 2
2
8h 0 k
n
n
k
37.
ЗаключениеНедостатки теории Бора:
• опирается одновременно как на классические
(орбитальная модель), так и на квантовые
представления (квантование энергии и момента
импульса) о
движении электронов, которые
противоречат друг другу;
• полностью объясняет спектр водорода, но более
сложные атомы (гелия, лития) описывает плохо.
38.
ЗаключениеНедостатки теории Бора:
опирается одновременно как на классические (орбитальная
модель), так и на квантовые представления (квантование
энергии и момента импульса) о движении электронов, которые
противоречат друг другу;
полностью объясняет спектр водорода, но более сложные атомы
(гелия, лития) описывает плохо.
Достоинства теории Бора:
• явилась переходным звеном между классической
физикой и современной квантовой механикой;
• впервые введено понятие квантового числа, как
характеристики состояния атома.
39.
Задание на самоподготовку1. Повторить тему лекции с использованием конспекта и
рекомендованной литературы.
2. Ответить на контрольные вопросы в электронном
учебнике по теме лекции.
3. Решить задачи в электронном учебнике по теме
лекции.






































 physics
physics








