Similar presentations:
Угол между прямыми в пространстве
1.
2.
Устная работаКак могут быть расположены прямые в
пространстве?
Прямые в пространстве могут быть
пересекающимися, параллельными,
скрещивающимися.
Какие прямые в пространстве называются
параллельными?
Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются.
3.
Устная работаКакие прямые в пространстве называются
скрещивающимися?
Две прямые называются скрещивающимися,
если они не лежат в одной плоскости
Сформулируйте признак скрещивающихся
прямых
Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту
плоскость в точке, не лежащей на первой
прямой, то эти прямые скрещивающиеся
4.
Устная работаВерно ли утверждение: если две прямые не
имеют общих точек, то они не пересекаются
Да, они параллельны или скрещиваются
Точка М не лежит на прямой а. Сколько
прямых, не пересекающих прямую а, проходит
через точку М? Сколько из них параллельны
прямой а?
Бесконечно много. Одна
Каким может быть взаимное расположение
двух прямых, одна из которых лежит в
плоскости, а другая параллельна этой
плоскости?
Параллельны или скрещиваются
5.
Устная работаВерно ли утверждение: если одна из двух
параллельных прямых параллельна
плоскости, то вторая прямая не пересекает
эту плоскость
Нет, она может лежать в плоскости
Каким может быть взаимное расположение
двух прямых, из которых одна параллельна
некоторой плоскости, а другая пересекает эту
плоскость?
Пересекаются или скрещиваются
6.
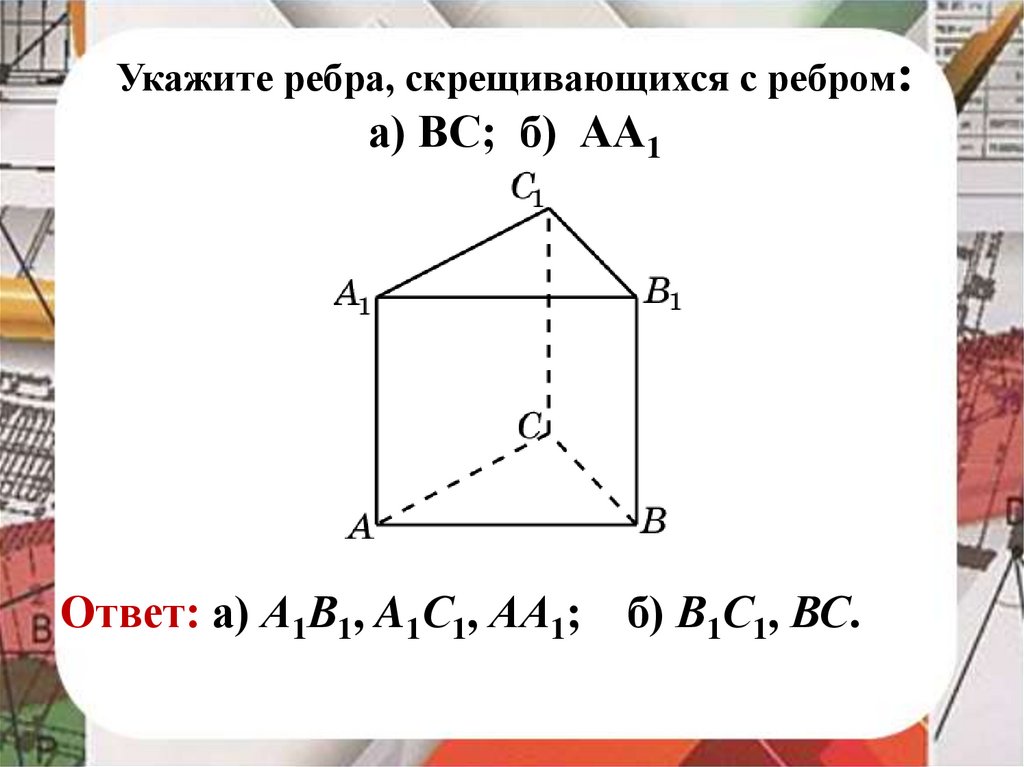
Укажите ребра, скрещивающихся с ребром:а) ВС; б) АА1
Ответ: а) А1В1, A1С1, АА1; б) В1С1, ВС.
7.
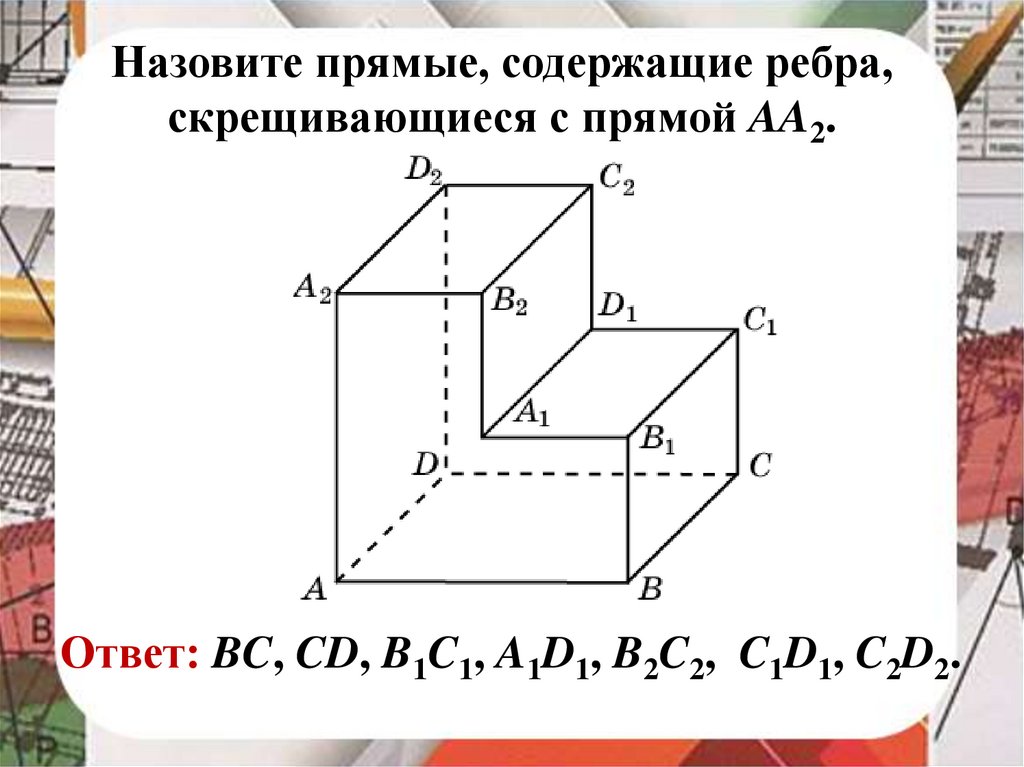
Назовите прямые, содержащие ребра,скрещивающиеся с прямой AA2.
Ответ: BC, CD, B1C1, A1D1, B2C2, C1D1, C2D2.
8.
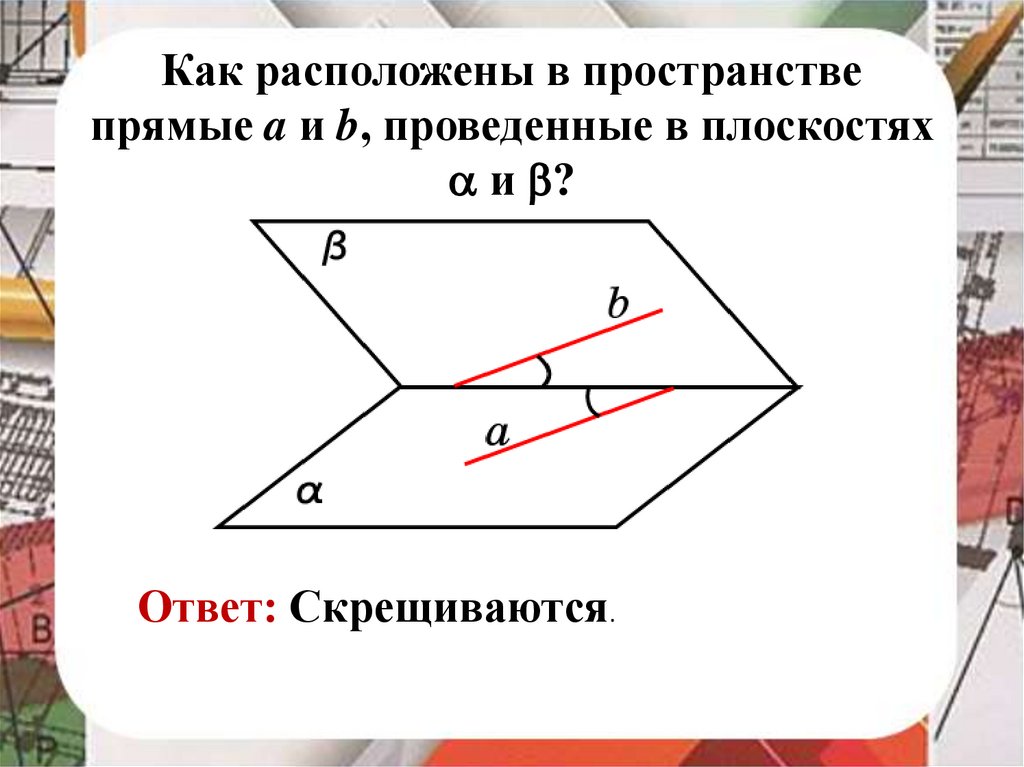
Как расположены в пространствепрямые a и b, проведенные в плоскостях
и ?
Ответ: Скрещиваются.
9.
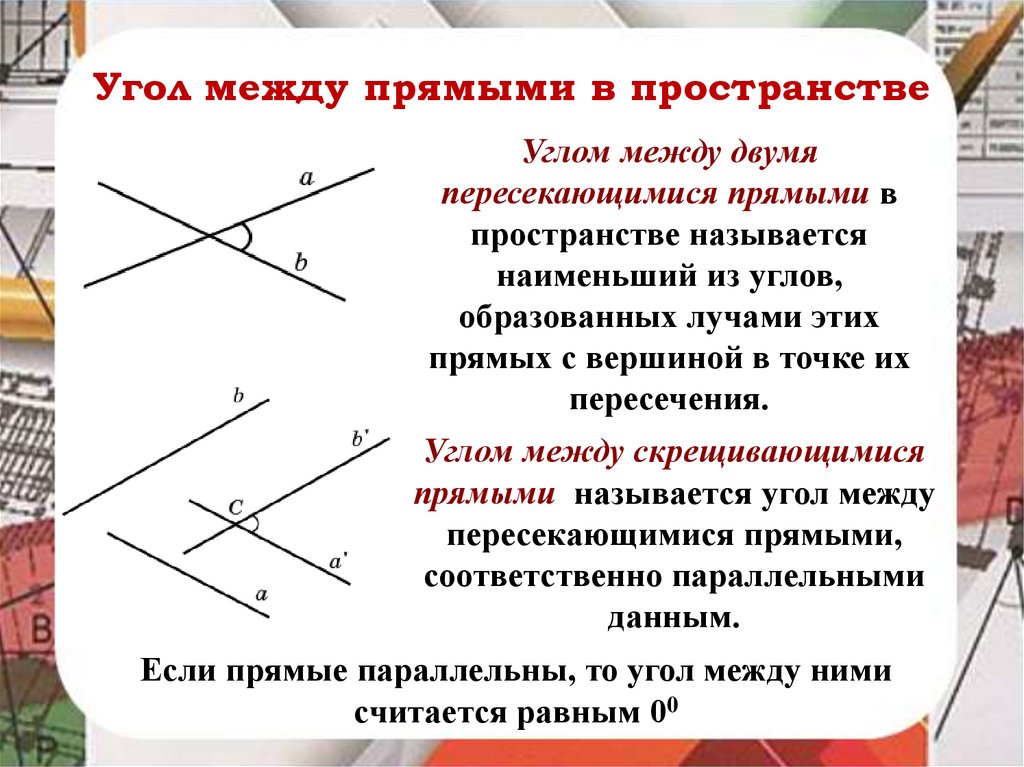
Угол между прямыми в пространствеУглом между двумя
пересекающимися прямыми в
пространстве называется
наименьший из углов,
образованных лучами этих
прямых с вершиной в точке их
пересечения.
Углом между скрещивающимися
прямыми называется угол между
пересекающимися прямыми,
соответственно параллельными
данным.
Если прямые параллельны, то угол между ними
считается равным 00
10.
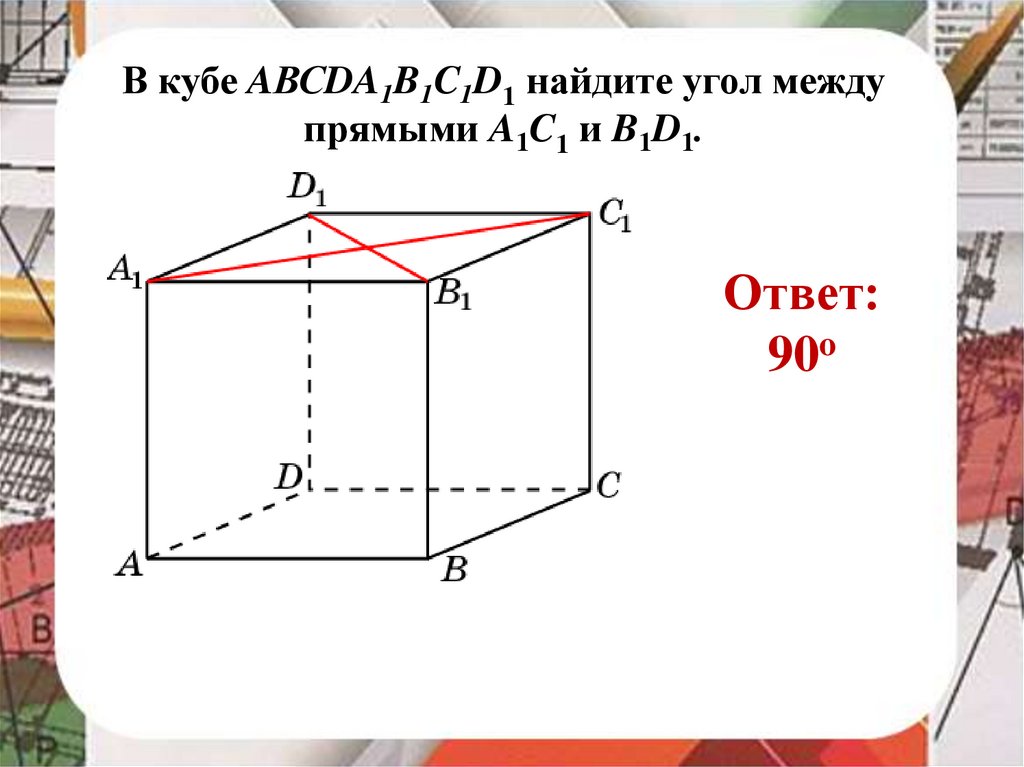
В кубе AВСDA1B1C1D1 найдите угол междупрямыми A1C1 и B1D1.
Ответ:
90o
11.
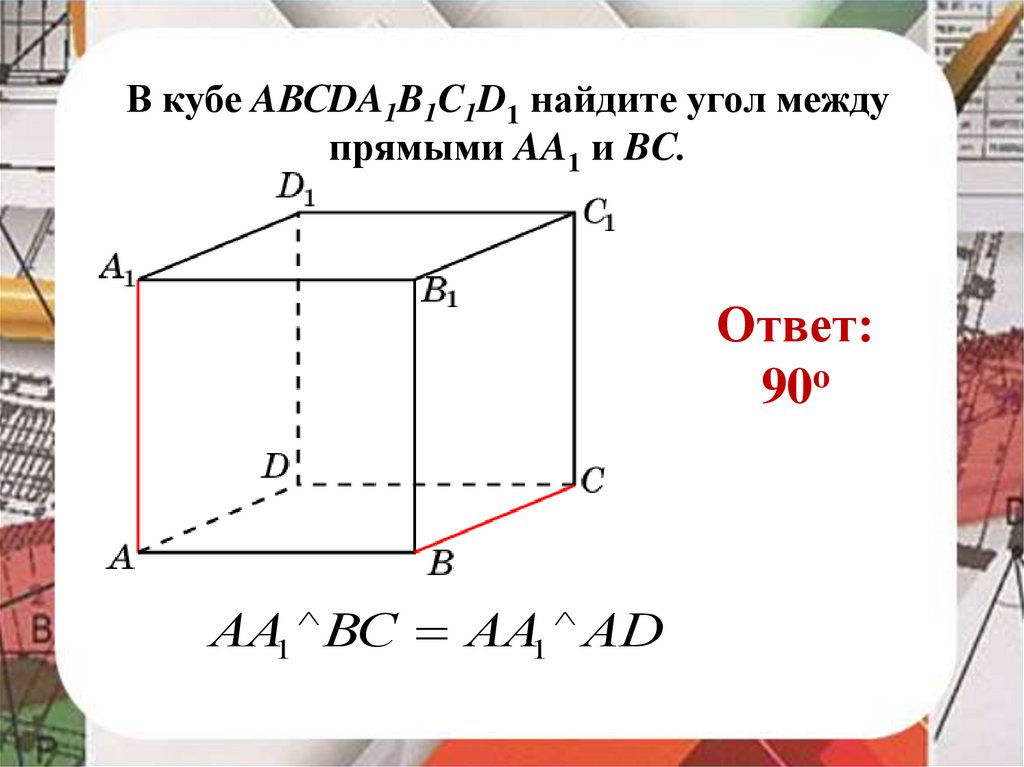
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AA1 и BC.
Ответ:
90o
АА1 ВС АА1 АD
12.
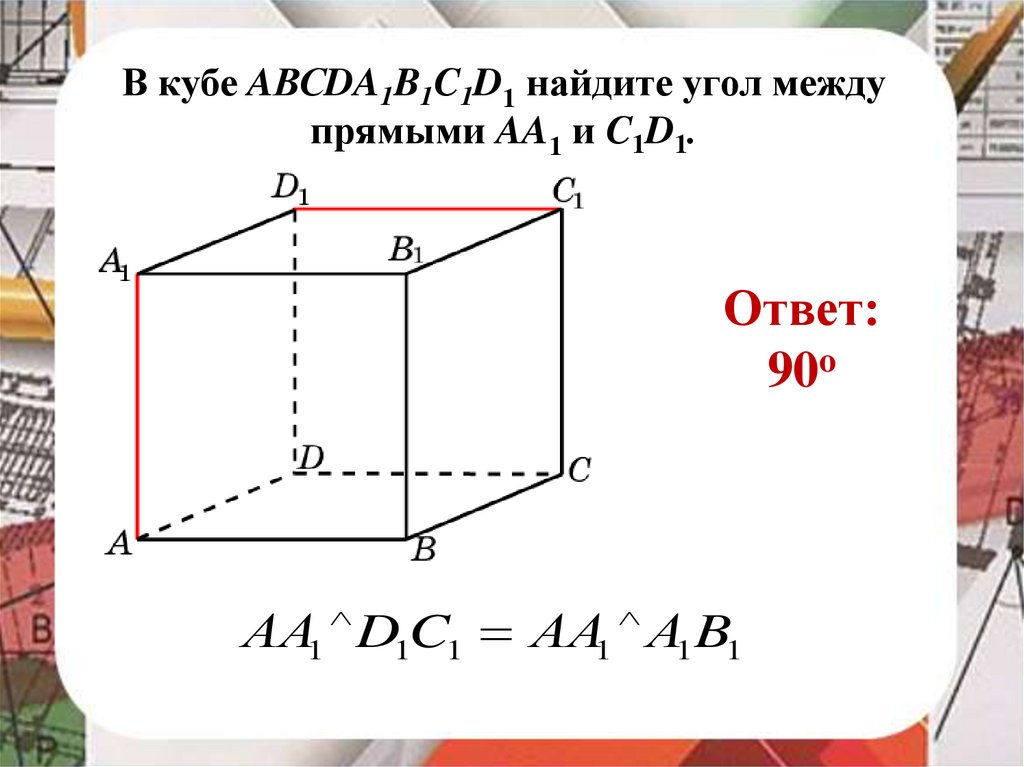
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AA1 и C1D1.
Ответ:
90o
АА1 D1C1 АА1 А1 B1
13.
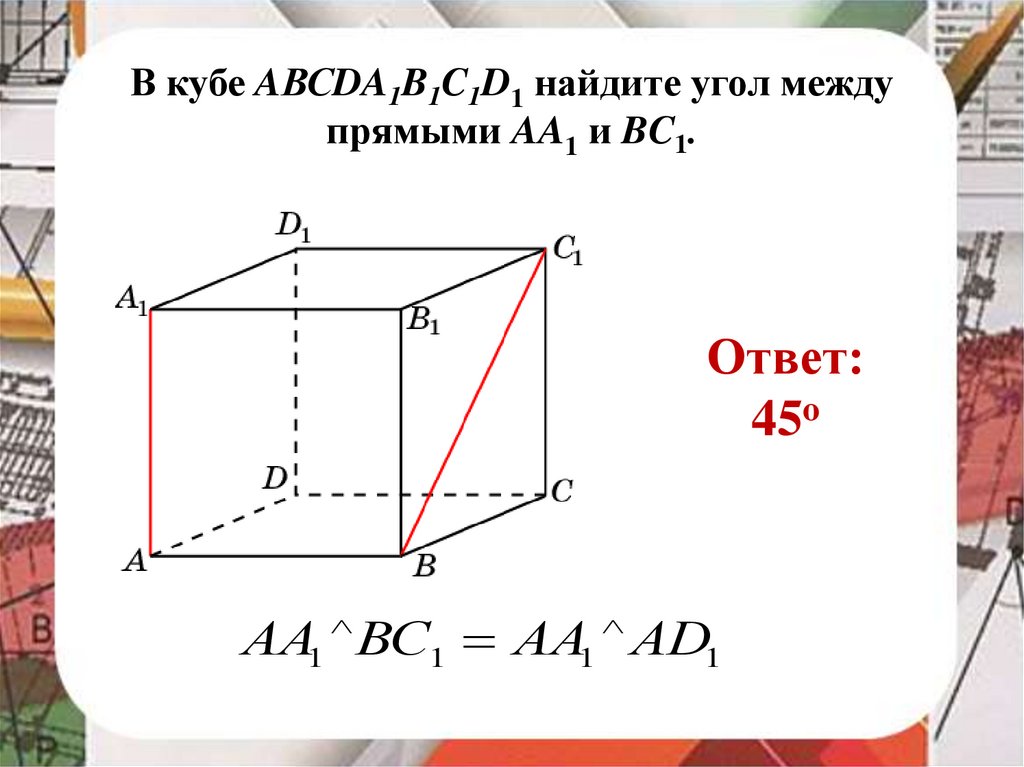
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AA1 и BC1.
Ответ:
45o
АА1 ВС1 АА1 АD1
14.
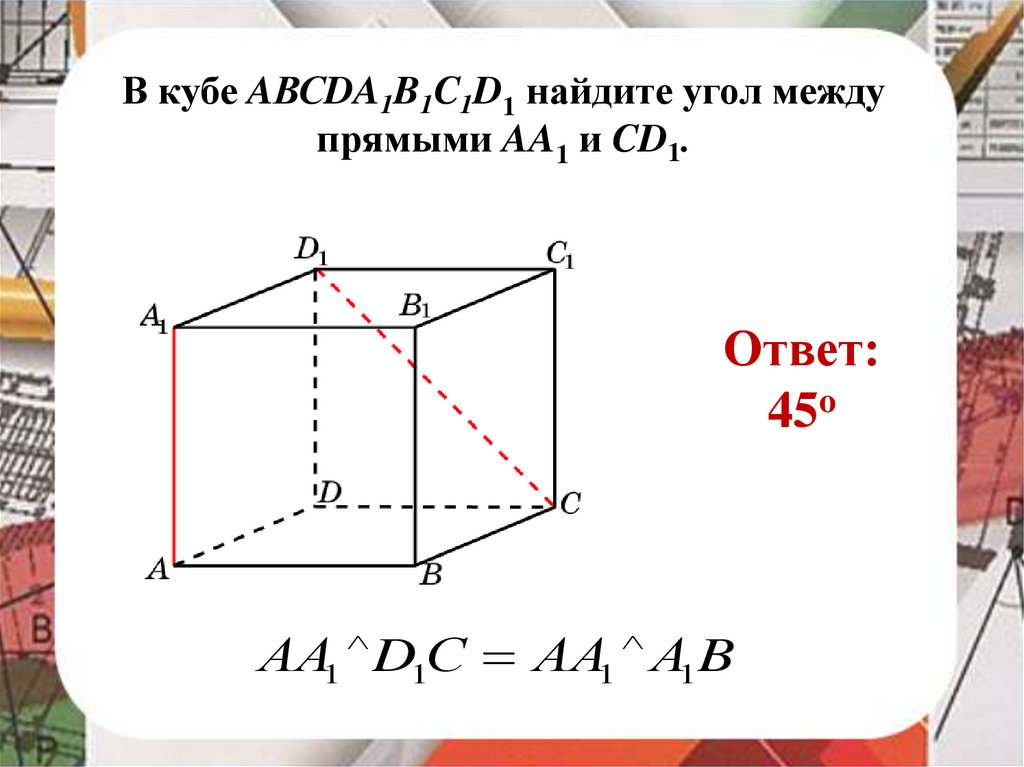
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AA1 и CD1.
Ответ:
45o
АА1 D1С АА1 А1 B
15.
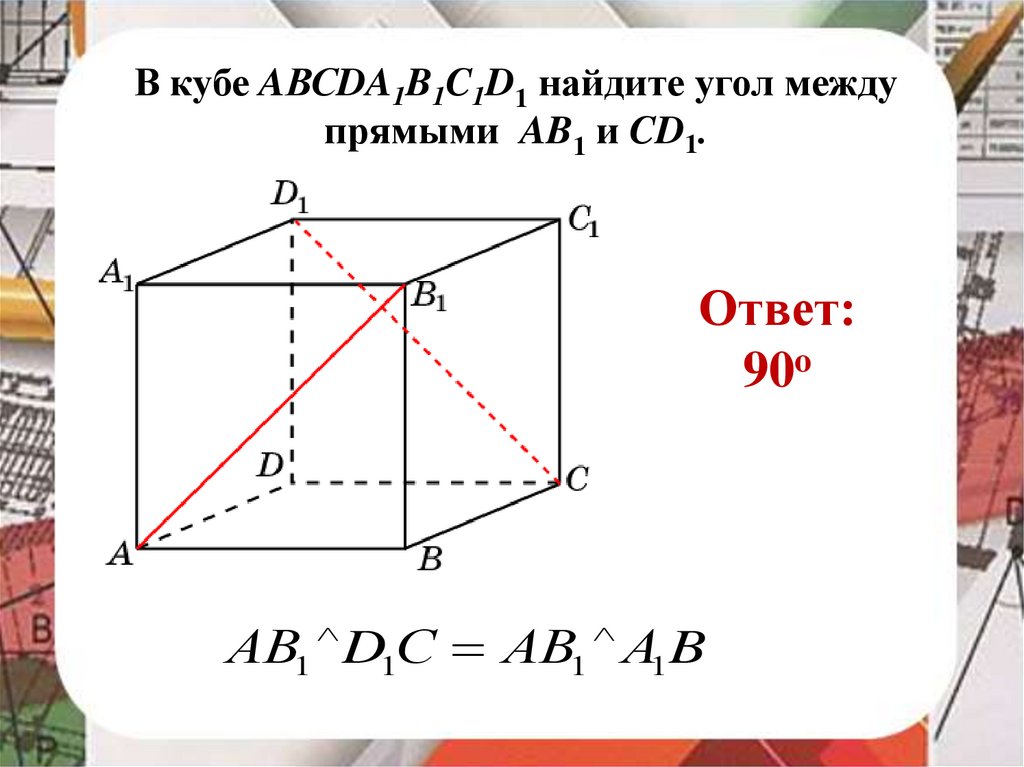
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AB1 и CD1.
Ответ:
90o
АВ1 D1С АВ1 А1 B
16.
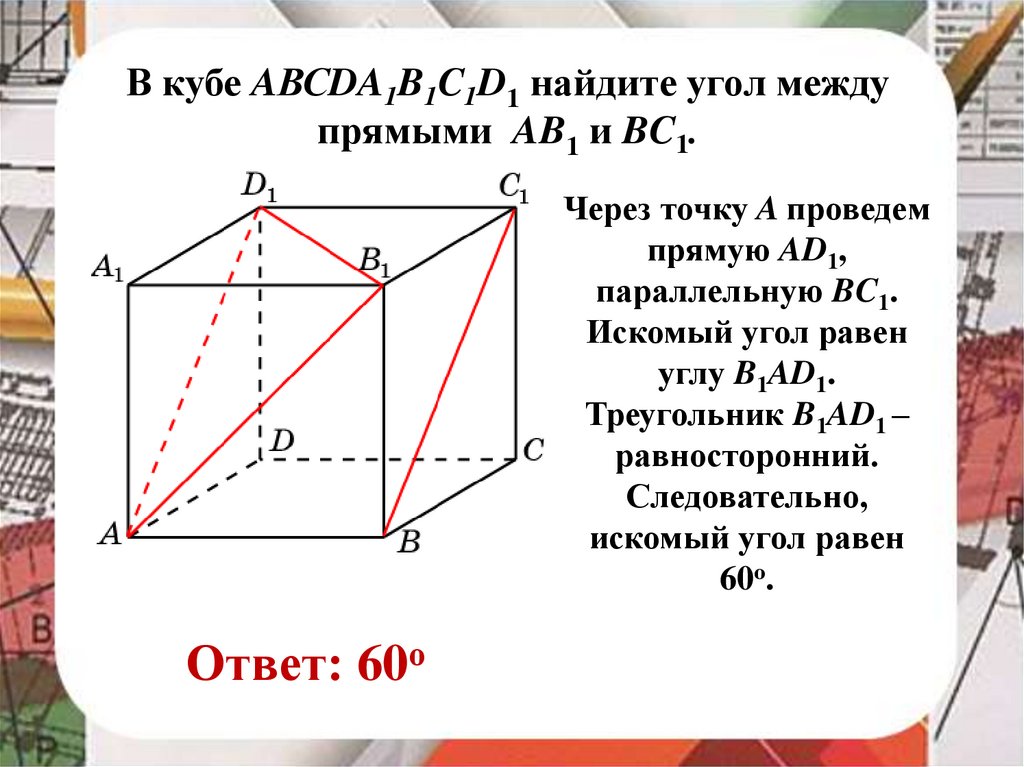
В кубе AВСDA1B1C1D1 найдите угол междупрямыми AB1 и BC1.
Через точку A проведем
прямую AD1,
параллельную BC1.
Искомый угол равен
углу B1AD1.
Треугольник B1AD1 –
равносторонний.
Следовательно,
искомый угол равен
60о.
Ответ: 60о
17.
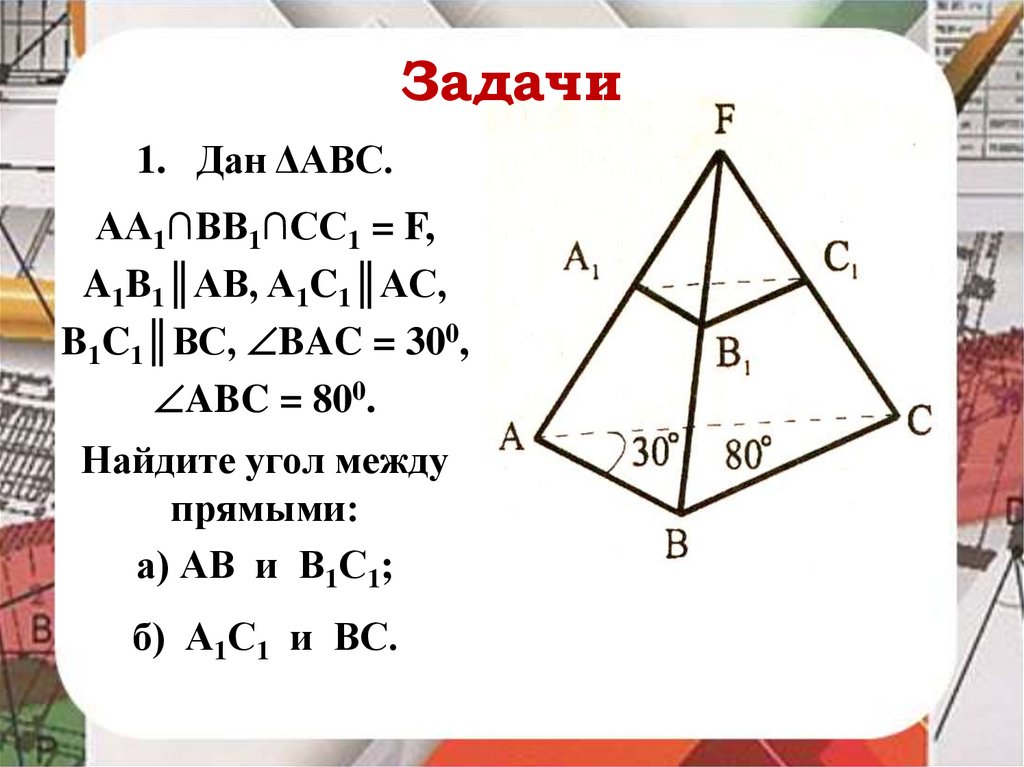
Задачи1. Дан ΔАВС.
АА1∩ВВ1∩СС1 = F,
A1B1║AB, A1C1║AC,
B1C1║BC, BAC = 300,
ABC = 800.
Найдите угол между
прямыми:
а) АВ и В1С1;
б) А1С1 и ВС.
18.
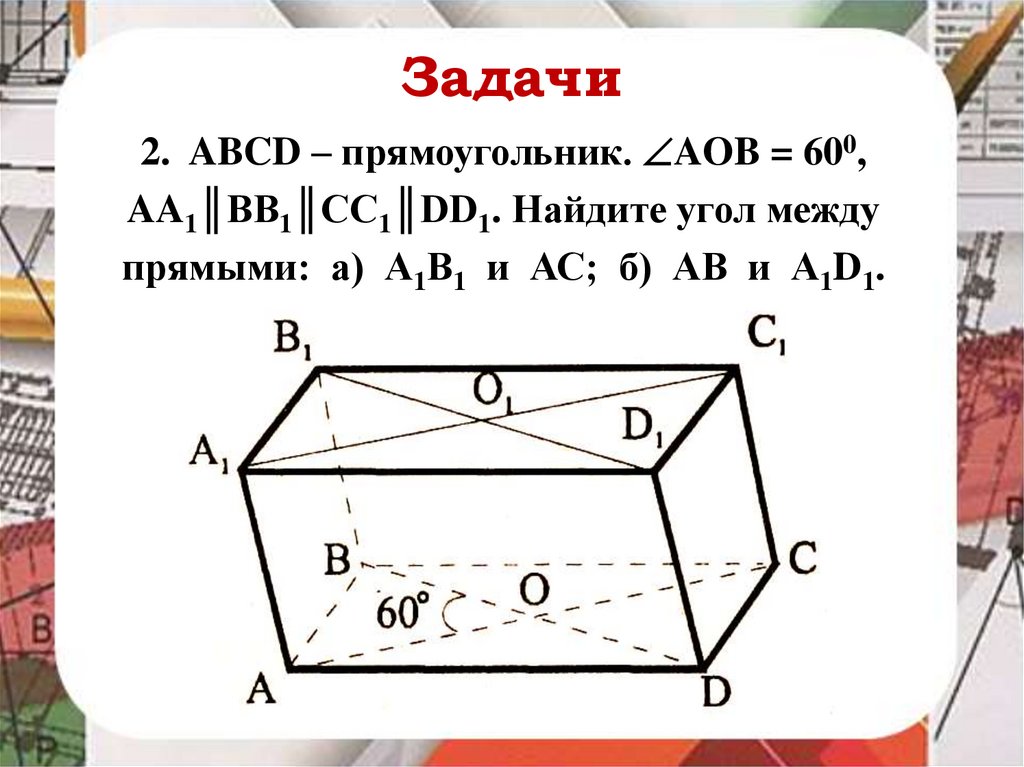
Задачи2. ABCD – прямоугольник. AOB = 600,
AA1║BB1║CC1║DD1. Найдите угол между
прямыми: а) А1В1 и АС; б) АВ и А1D1.
19.
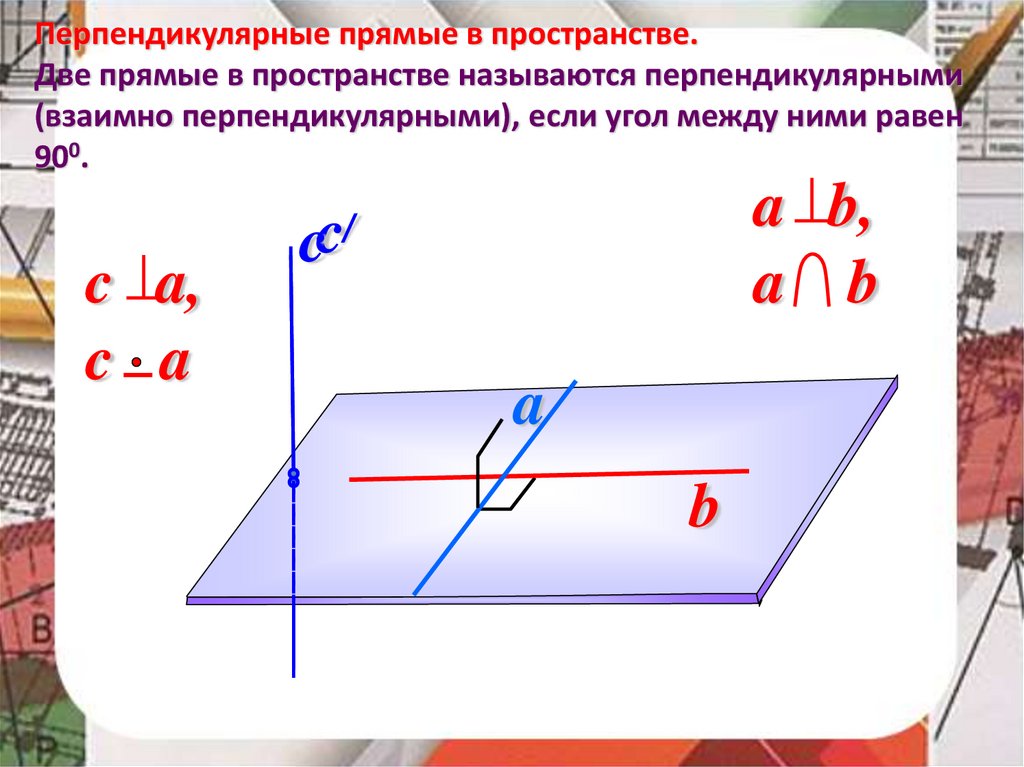
Перпендикулярные прямые в пространстве.Две прямые в пространстве называются перпендикулярными
(взаимно перпендикулярными), если угол между ними равен
900.
c a,
c a
a b,
a b
/
c
c
a
b
20.
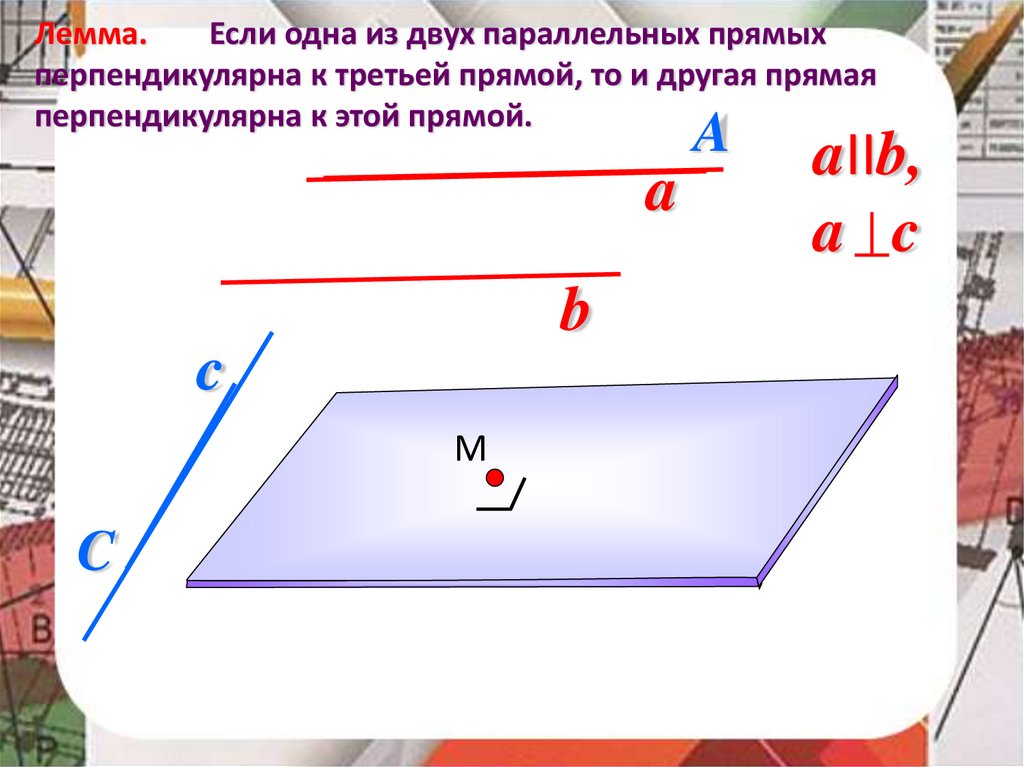
Лемма.Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая прямая
перпендикулярна к этой прямой.
A
a
b
c
M
C
aIIb,
a c
21.
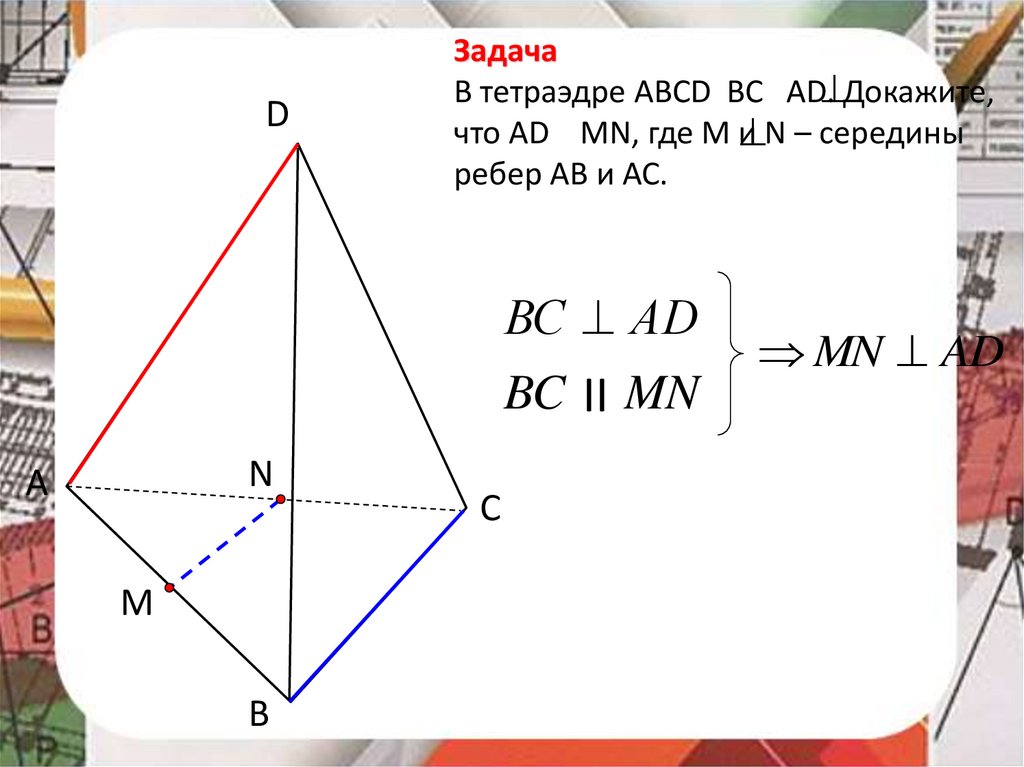
DЗадача
В тетраэдре АВСD ВС АD. Докажите,
что АD MN, где М и
N – середины
ребер АВ и АС.
ВС АD
BC II MN
N
А
M
B
C
MN AD
22.
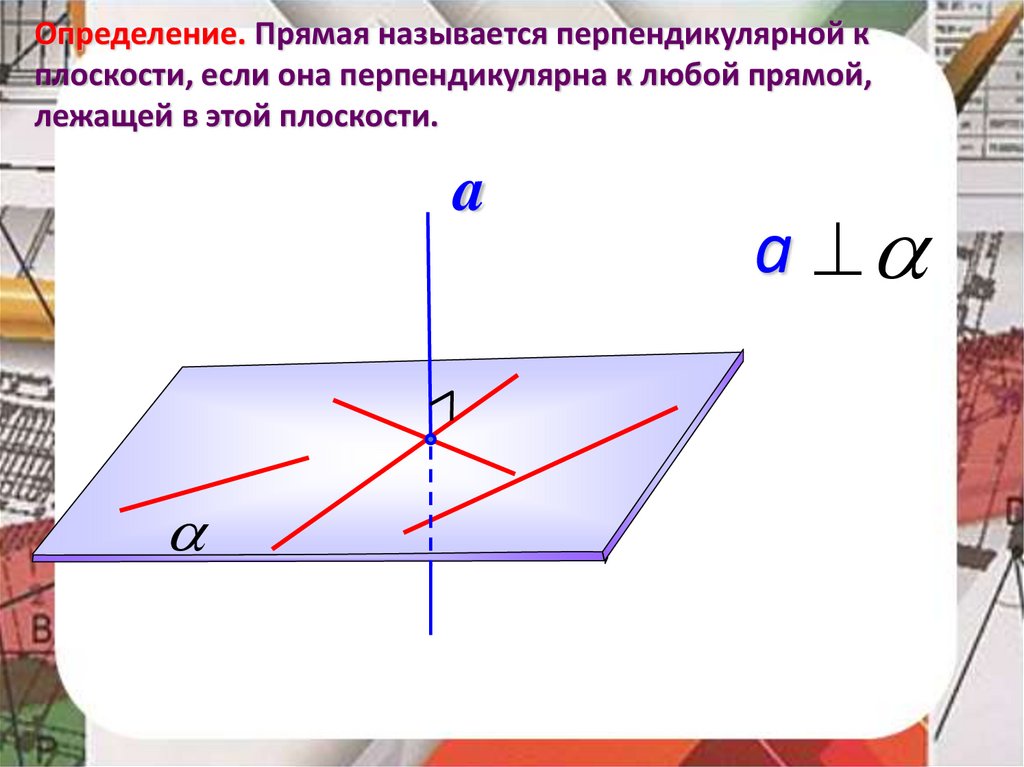
Определение. Прямая называется перпендикулярной кплоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
a
23.
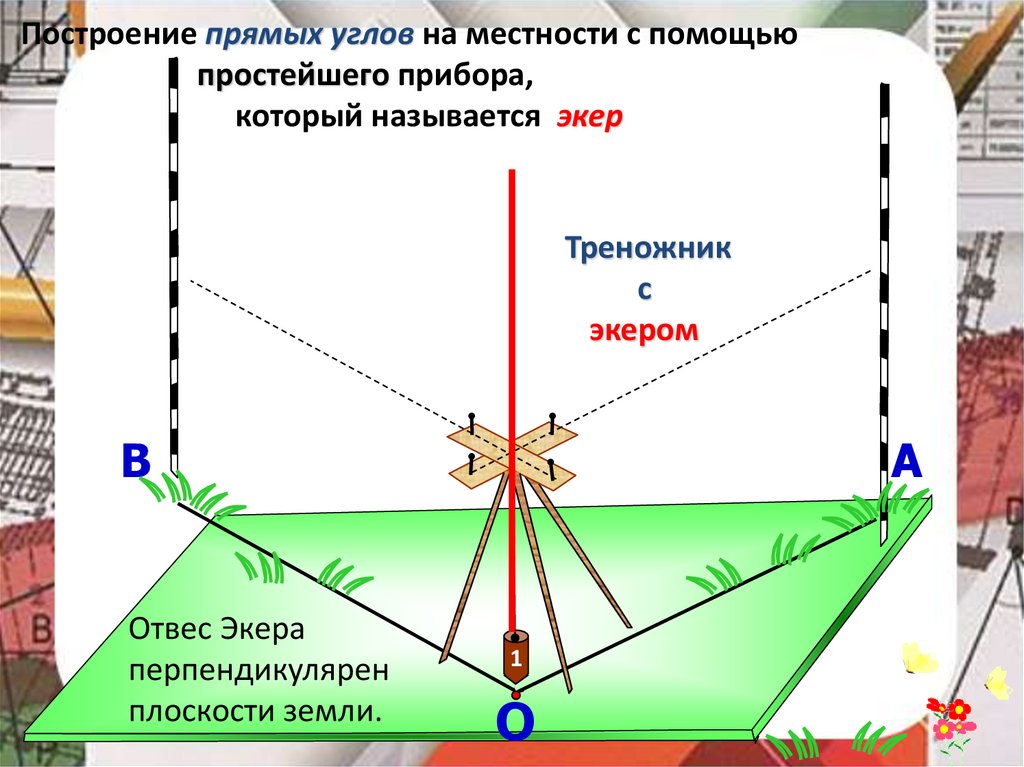
Построение прямых углов на местности с помощьюпростейшего прибора,
который называется экер
Треножник
с
экером
В
Отвес Экера
перпендикулярен
плоскости земли.
А
1
О
24.
Канат в спортивном залеперпендикулярен плоскости
пола.
25.
26.
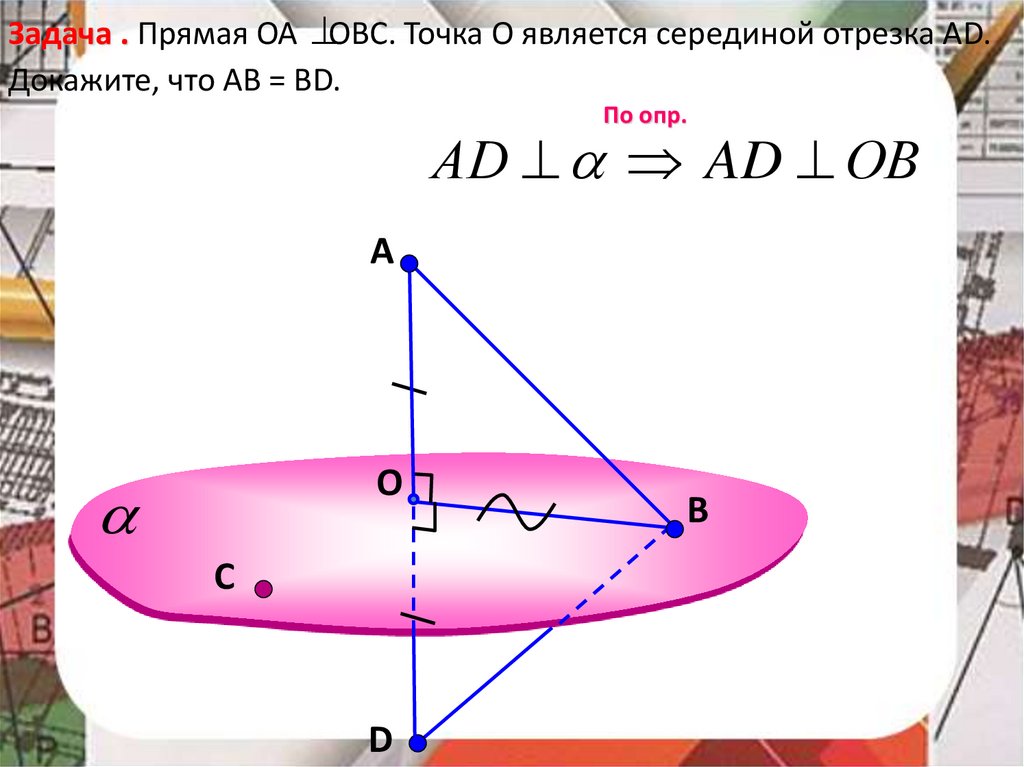
Задача . Прямая ОА OBC. Точка О является серединой отрезка АD.Докажите, что АВ = ВD.
По опр.
АD AD ОВ
A
O
С
D
В
27.
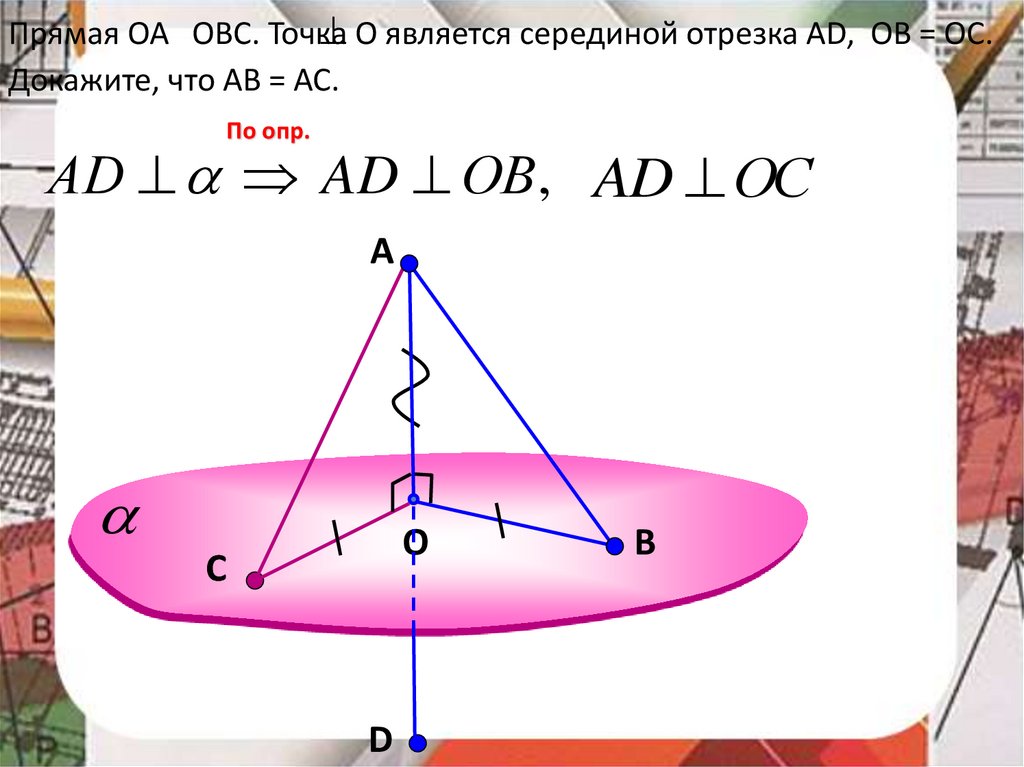
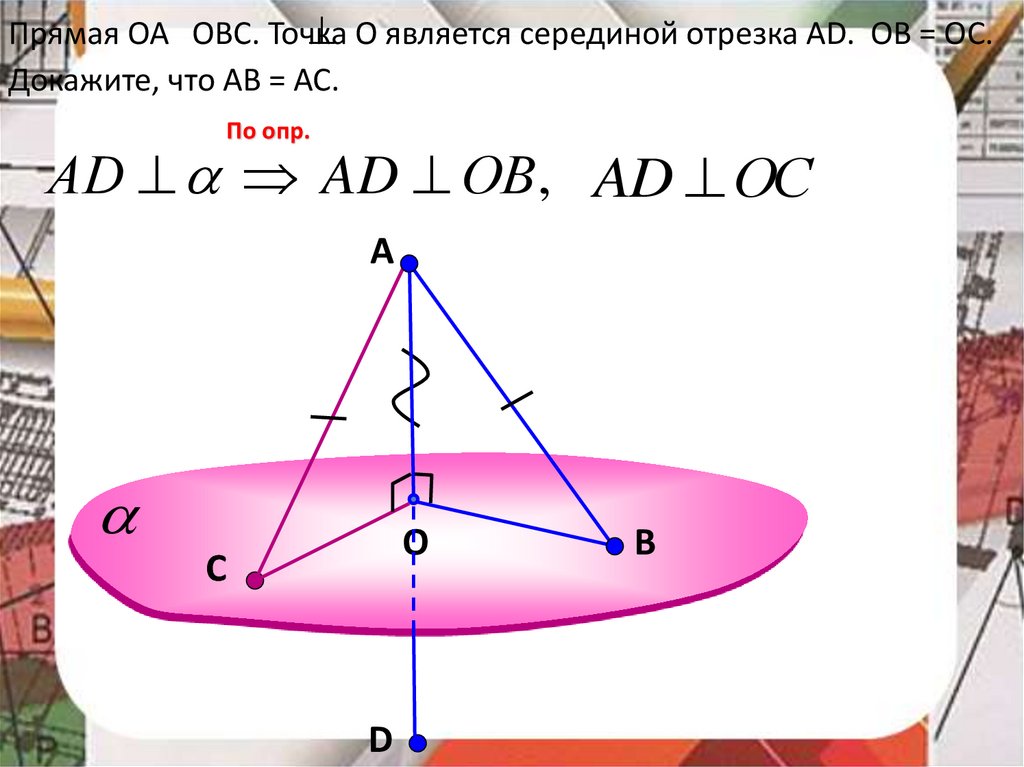
О является серединой отрезка АD, ОВ = ОС.Прямая ОА OBC. Точка
Докажите, что АВ = АС.
По опр.
АD AD ОВ , AD ОС
A
O
С
D
В
28.
О является серединой отрезка АD. ОВ = ОС.Прямая ОА OBC. Точка
Докажите, что АВ = АС.
По опр.
АD AD ОВ , AD ОС
A
O
С
D
В
29.
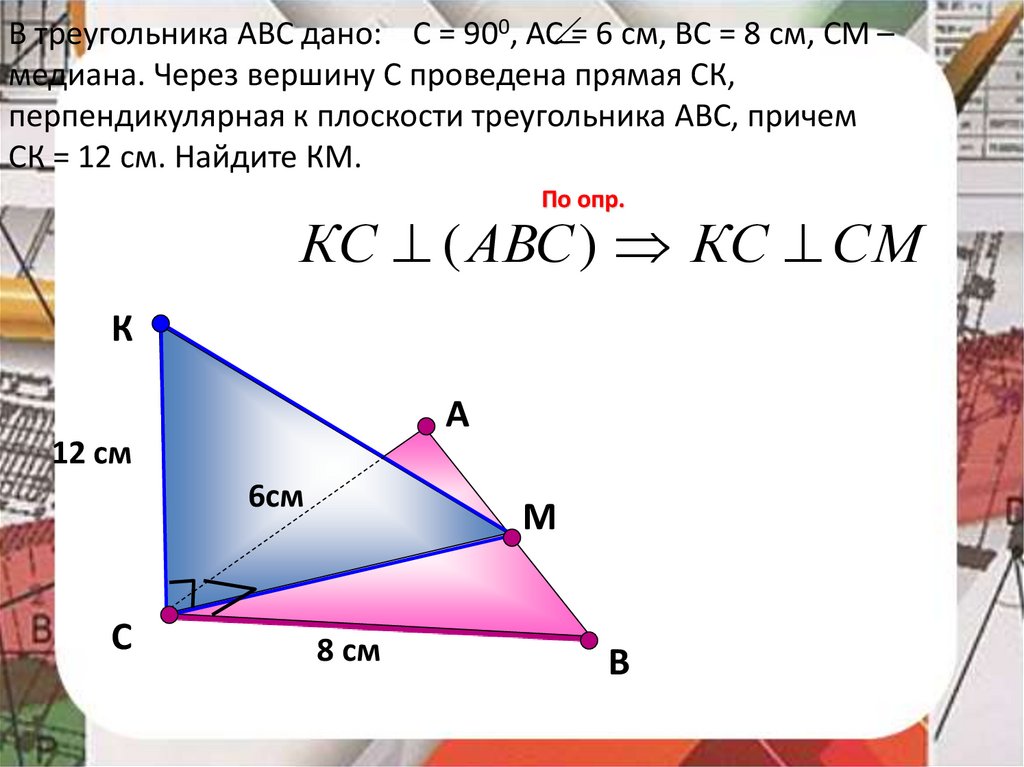
В треугольника АВС дано: С = 900, АС = 6 см, ВС = 8 см, СМ –медиана. Через вершину С проведена прямая СК,
перпендикулярная к плоскости треугольника АВС, причем
СК = 12 см. Найдите КМ.
По опр.
КС ( АВС ) КС СМ
К
А
12 см
6см
С
М
8 см
В
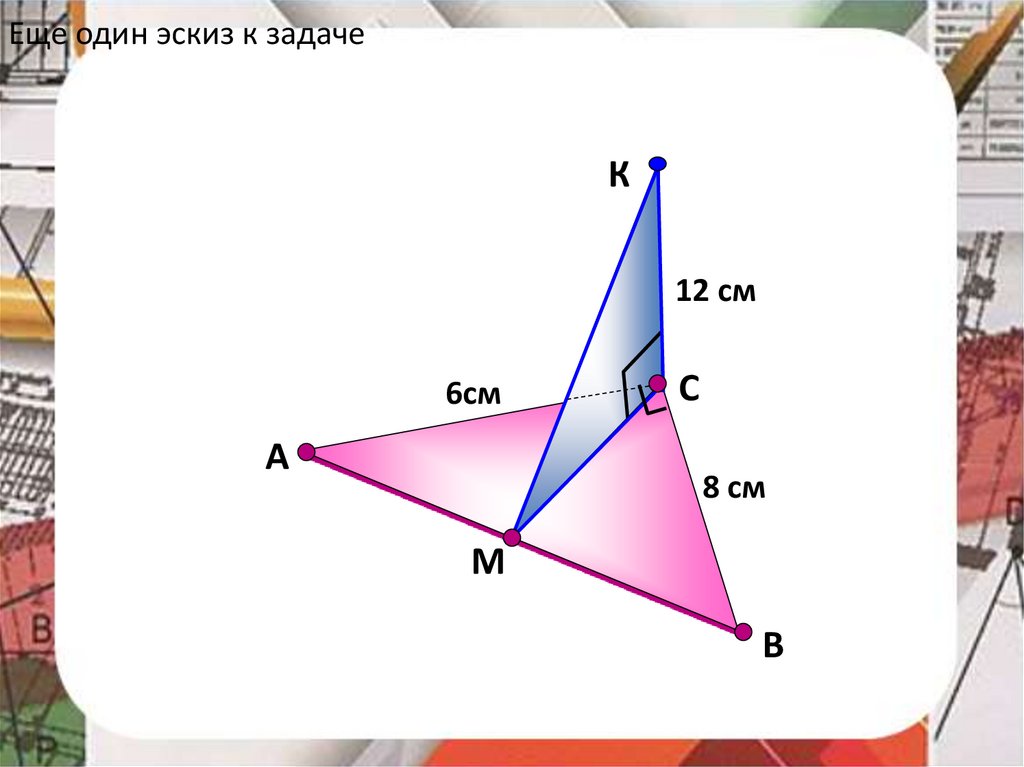
30.
Еще один эскиз к задачеК
12 см
6см
А
С
8 см
М
В
31.
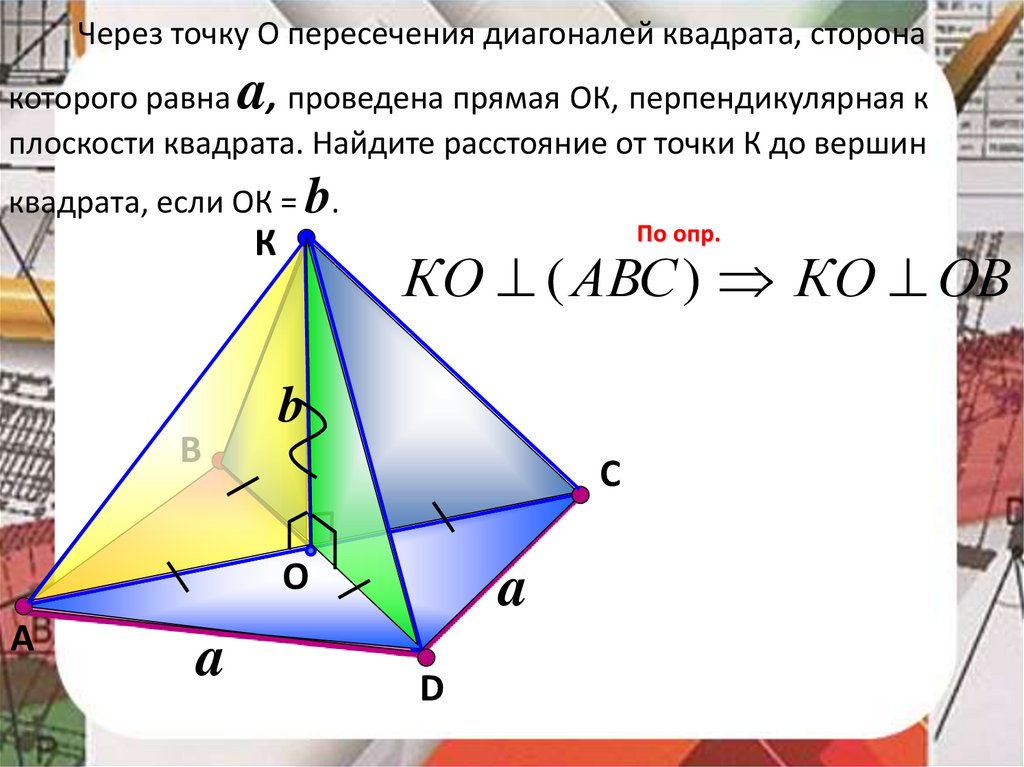
Через точку О пересечения диагоналей квадрата, сторонаa
которого равна , проведена прямая ОК, перпендикулярная к
плоскости квадрата. Найдите расстояние от точки К до вершин
квадрата, если ОК = b.
К
В
По опр.
КО ( АВС ) КО ОВ
b
С
O
А
a
a
D
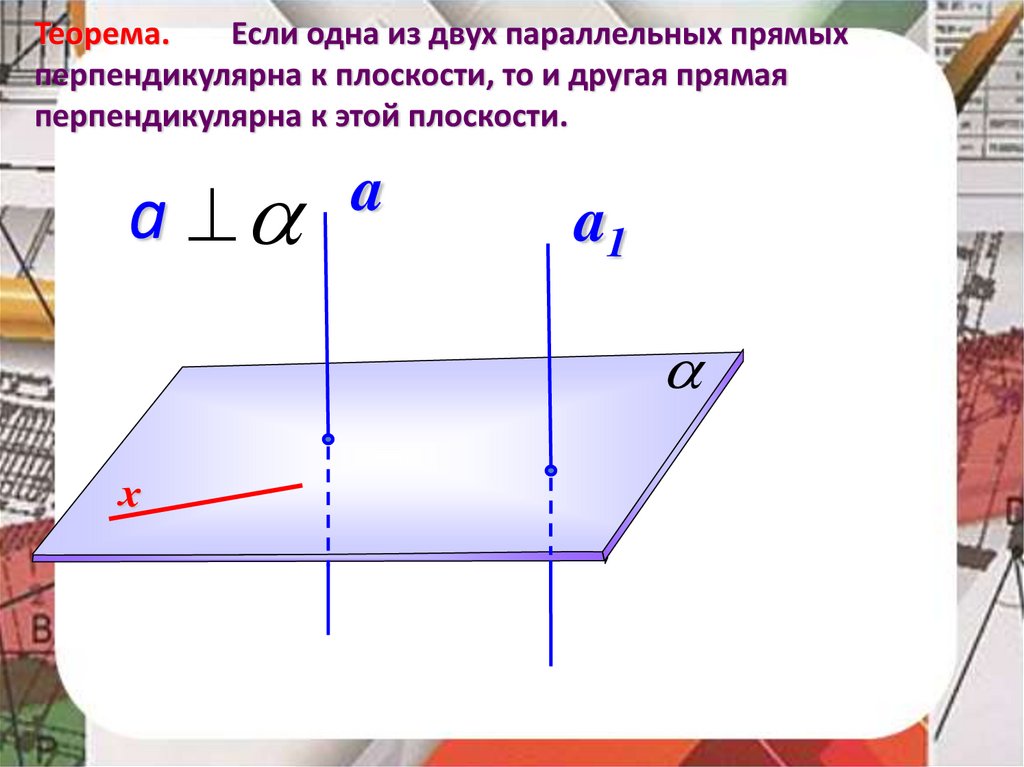
32.
Теорема.Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая прямая
перпендикулярна к этой плоскости.
a
a
a1
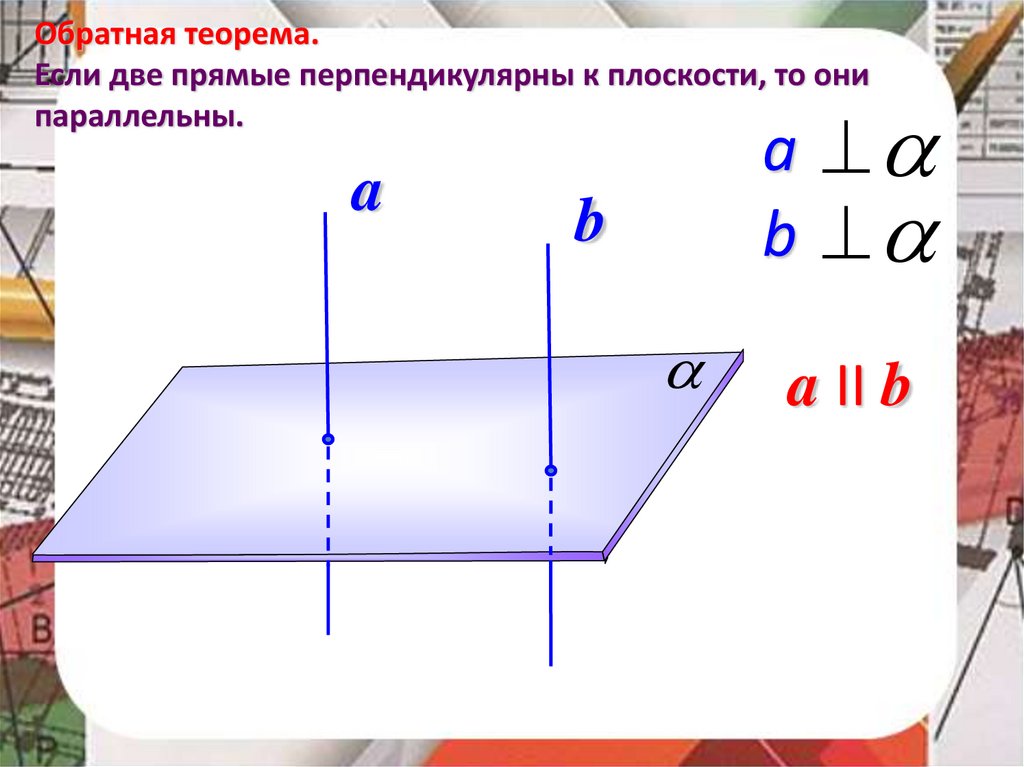
33.
Обратная теорема.Если две прямые перпендикулярны к плоскости, то они
параллельны.
a
a
b
b
a II b
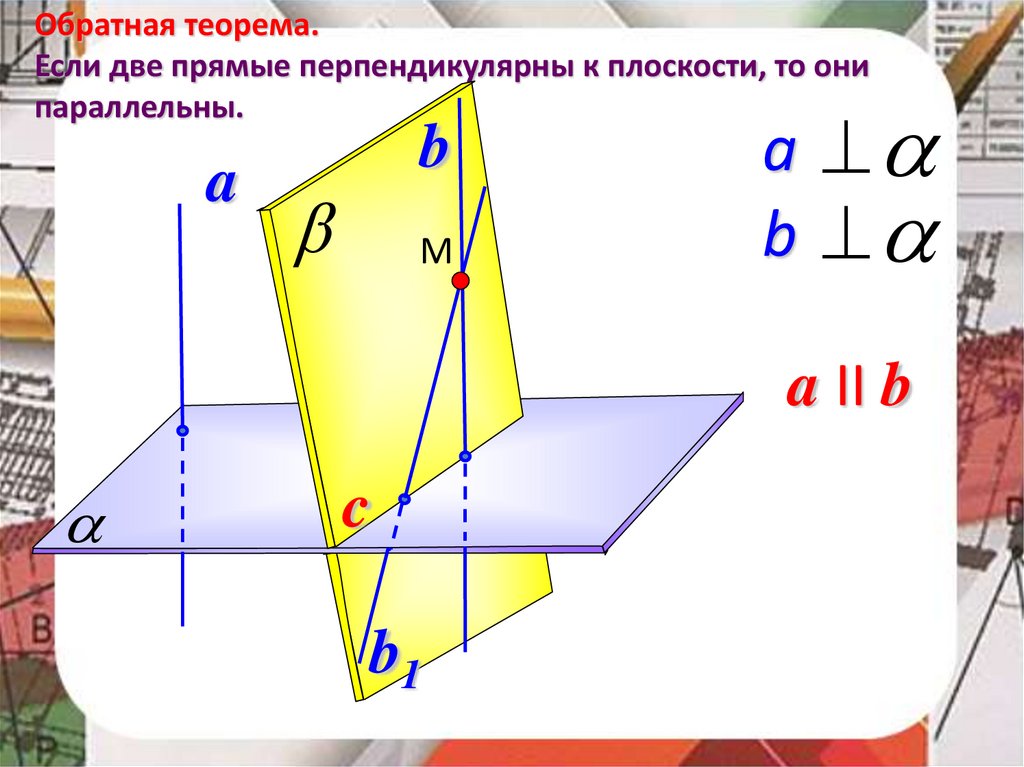
34.
Обратная теорема.Если две прямые перпендикулярны к плоскости, то они
параллельны.
a
b
M
a
b
a II b
c
b1
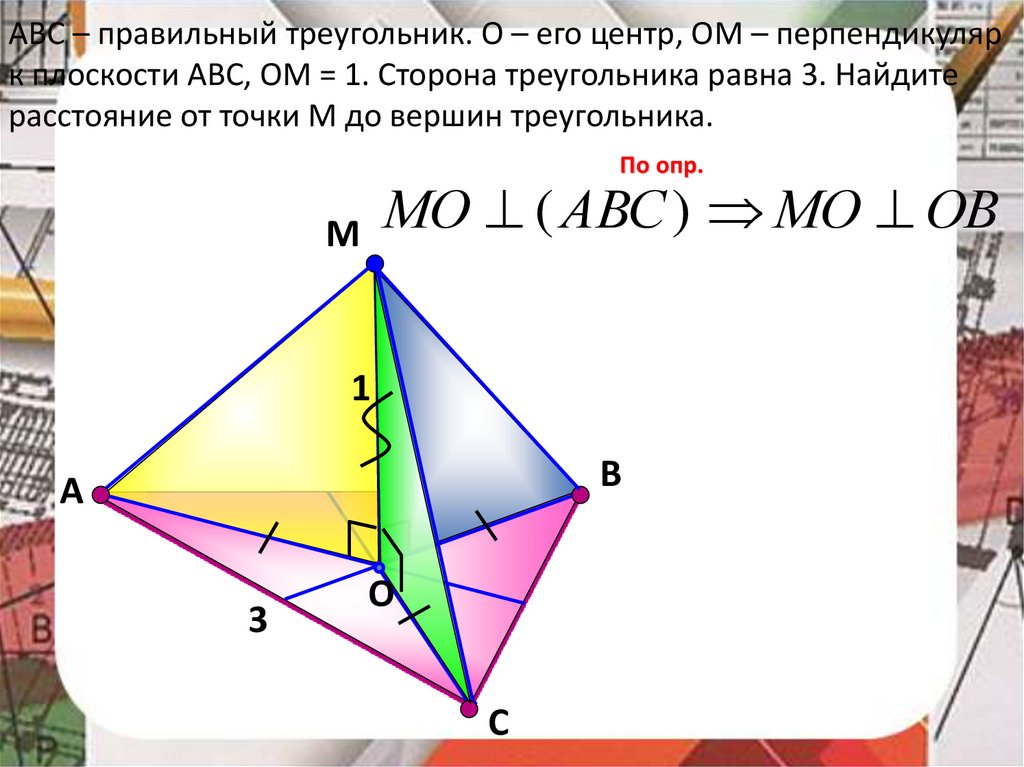
35.
АВС – правильный треугольник. О – его центр, ОМ – перпендикулярк плоскости АВС, ОМ = 1. Сторона треугольника равна 3. Найдите
расстояние от точки М до вершин треугольника.
По опр.
МО ( АВС ) МО ОВ
М
1
В
А
3
O
С
36.
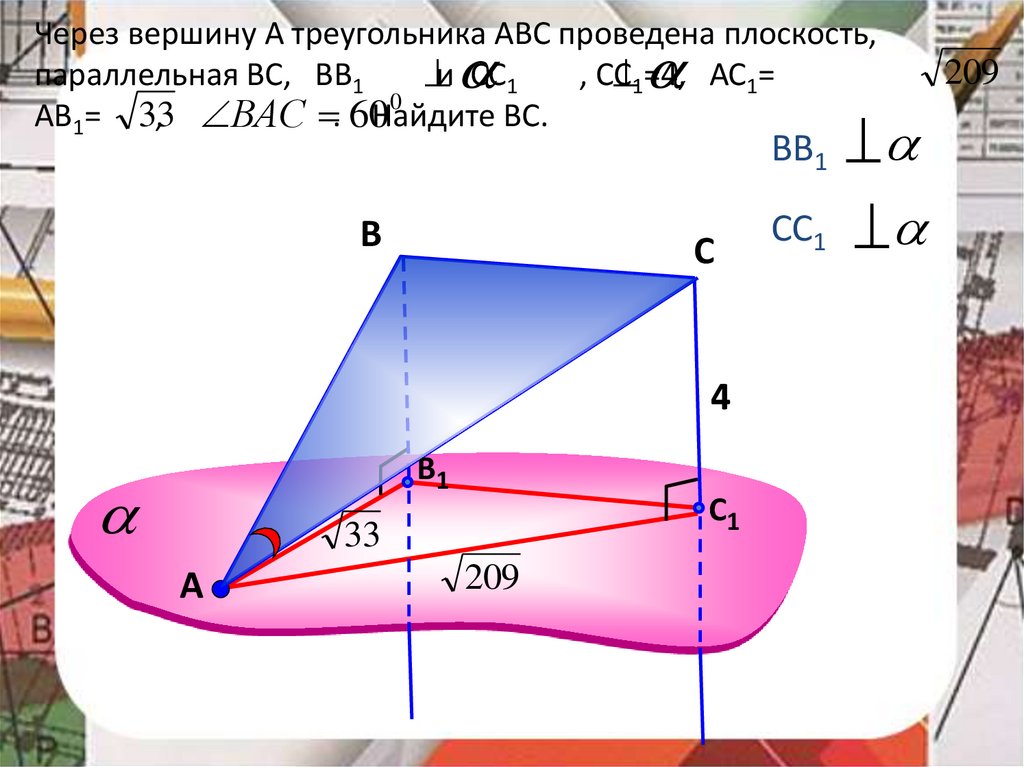
Через вершину А треугольника АВС проведена плоскость,параллельная ВС, ВВ1
, СС
и СС1
1=4, АС1=
0
АВ1= 33
, ВАС . 60
Найдите ВС.
В
С
4
В1
С1
33
А
209
209
ВВ1
СС1
37.
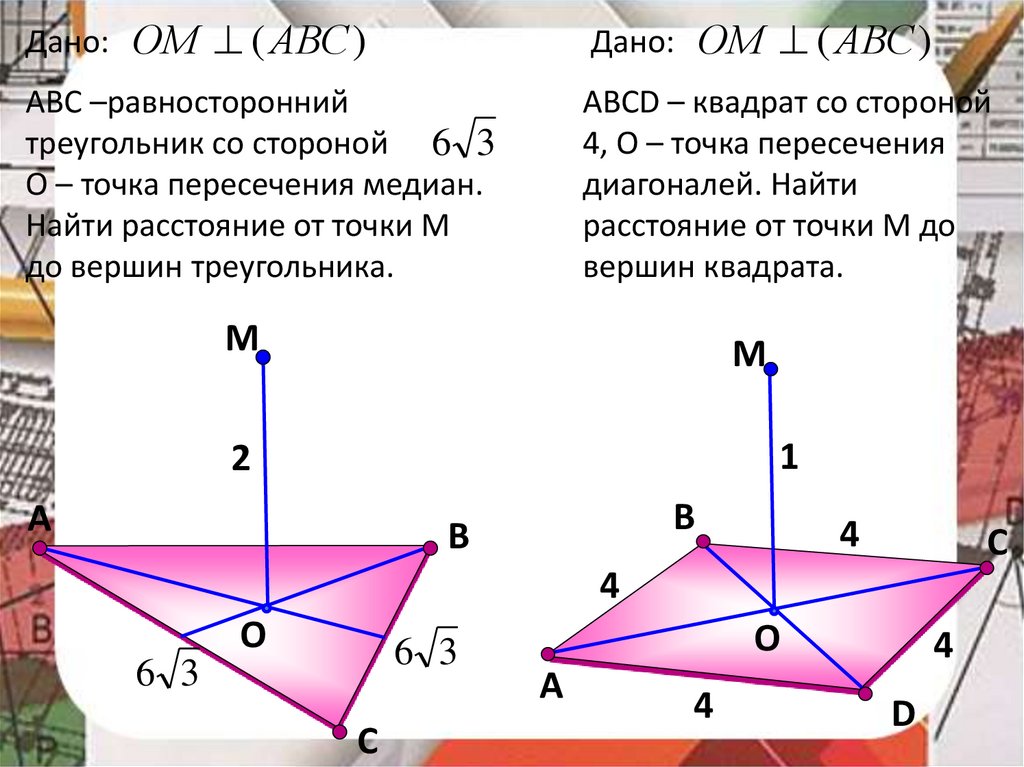
Дано:ОМ ( АВС )
ОМ ( АВС )
Дано:
АВС –равносторонний
треугольник со стороной 6 3
О – точка пересечения медиан.
Найти расстояние от точки М
до вершин треугольника.
АВСD – квадрат со стороной
4, О – точка пересечения
диагоналей. Найти
расстояние от точки М до
вершин квадрата.
М
М
1
2
А
В
В
4
С
4
O
6 3
6 3
С
O
А
4
4
D
38.
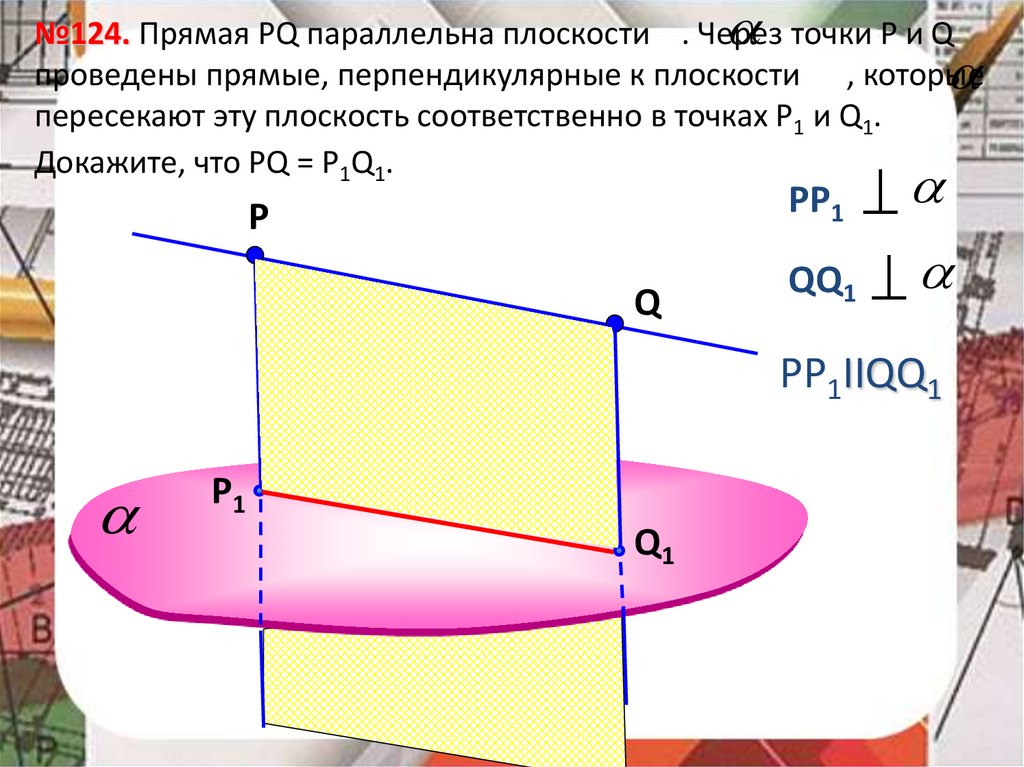
№124. Прямая РQ параллельна плоскости . Черезточки Р и Q
проведены прямые, перпендикулярные к плоскости , которые
пересекают эту плоскость соответственно в точках Р1 и Q1.
Докажите, что РQ = P1Q1.
Р
Q
РР1
QQ1
PP1IIQQ1
P1
Q1
39.
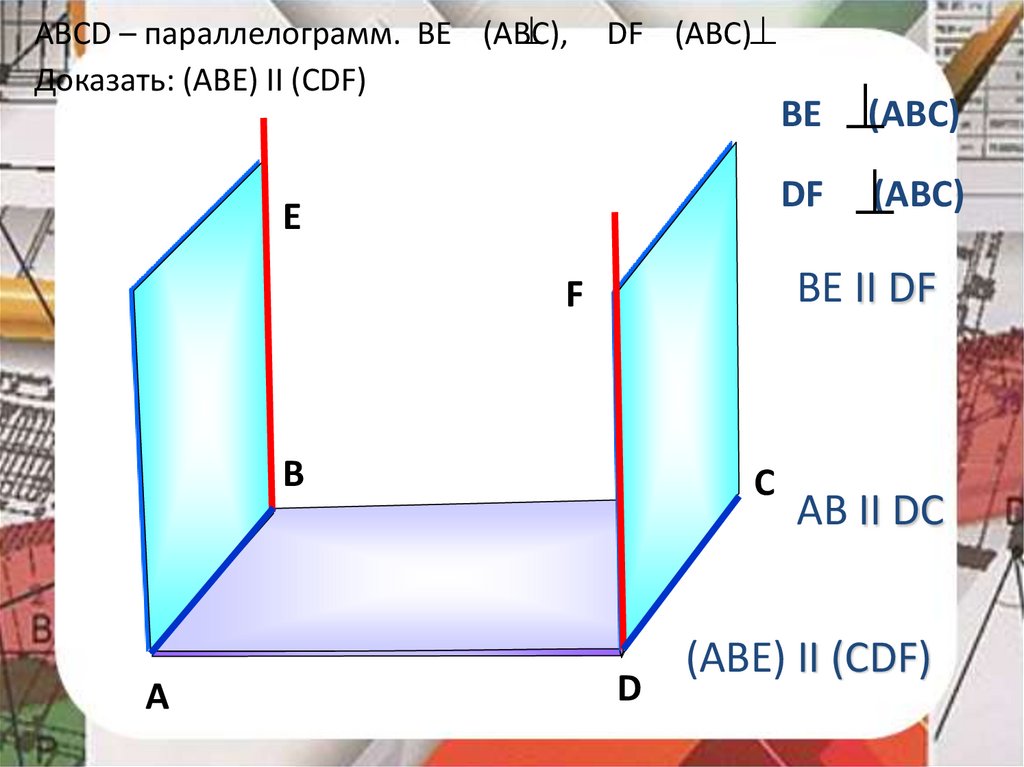
ABCD – параллелограмм. BE (ABC),Доказать: (АВЕ) II (СDF)
DF (ABC)
Е
(АВС)
DF
(АВС)
ВЕ II DF
F
В
А
ВЕ
С
D
AB II DC
(ABЕ) II (CDF)
40.
Задача. Через точки Р и Q прямой PQ проведены прямые,перпендикулярные к плоскости , которые пересекают эту
плоскость соответственно в точках Р1 и Q1. Найдите Р1Q1.
15
Q
Р
33,5
21,5
P1
Q1
По опр.
РР1 РР1 Р1Q1 ,
РР1
QQ1
PP1IIQQ1








 mathematics
mathematics








