Элементы математической логики. Логические функции Excel. (Лекция 6)

1. Лекция №6

Элементы математической
логики. Логические функции Excel.

2.

• Логика - это наука, изучающая правильность
суждений, рассуждений и доказательств.
• Суждение истинно, если оно отражает
действительное положение вещей. Примеры
истинных суждений: «снег белый», «2´2 = 4»,
«театр - это искусство».
• Суждение ложно, если оно противоречит
истинному положению вещей. Примеры
ложных утверждений - «2´2 = 5», «снег черный», «Земля плоская».
• Математическая логика - это дисциплина,
изучающая технику математических
доказательств.

3.

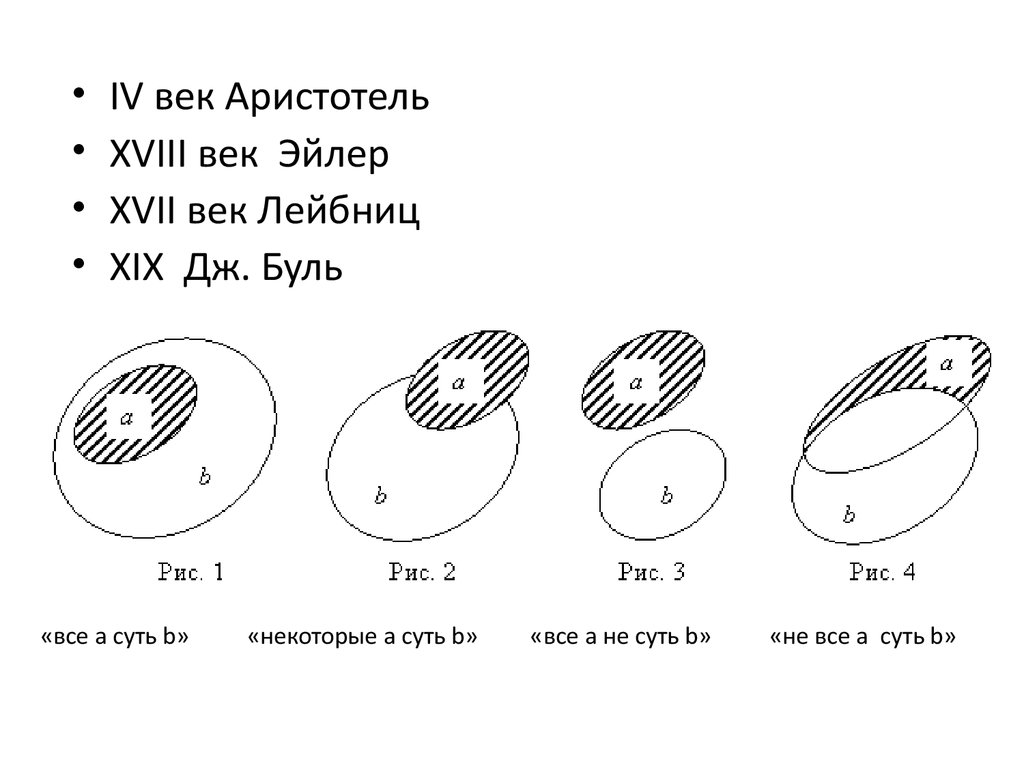
IV век Аристотель
XVIII век Эйлер
XVII век Лейбниц
XIX Дж. Буль
«все a суть b»
«некоторые a суть b»
«все a не суть b»
«не все a суть b»

4. Логика высказываний

• высказывание – любое повествовательное
предложение, про которое известно, является оно
истинным или ложным.
а)«сумма чисел 2 и 5 равна 7» (истинное высказывание),
б) «2 + 5 = 7» — предыдущее высказывание, записанное
с помощью математических символов,
в) «для всех значений x верно
неравенство
(ложное высказывание),
г) «завтра будет солнечный день» (может быть истинным
или ложным).
Высказывания обозначаются заглавными буквами
латинского алфавита – A, B и т.д.

5.

• высказывательные формы (предикаты)
– предложения, содержащие переменную.
Например, выражение «
»

6.

«У кошки 4 ноги»;
«Сумма углов треугольника равна 180°»;
«Температура кипения воды 180°»;
«У квадрата есть прямой угол»;
«2x = 3y»;
«Число 5 делится на 2 без остатка»;
«x < 5»;
«У квадрата есть только один прямой угол»;
«a + b = 10»;
«Дважды два – четыре»;
«Пустое множество не имеет подмножеств».

7. Простые и сложные высказывания

Простые и сложные высказывания
• Высказывание имеет вид повествовательного
предложения. Из двух таких предложений можно
получить новые с помощью логических связок –
союзов «и», «или», « если…,то», «тогда и только
тогда, когда» и частицы «не». Такие предложения
будем называть составными.
• Предложения, не являющиеся составными,
называются элементарными.
• Соответственно, если можно судить об истинности
или ложности таких предложений, то они будут
называться простыми и составными
высказываниями.

8. Логические операции над высказываниями

• Высказывание «А и В», истинное, если
истинны оба высказывания А и В, и ложное,
если хотя бы одно из них ложно, называется
конъюнкцией этих высказываний
и обозначается А^В.
• Высказывание «А или В», истинное, если
истинно хотя бы одно из высказываний А или
В, и ложное лишь в одном случае, когда оба
высказывания А и В ложны, называется
дизъюнкцией этих высказываний
и обозначается А В.

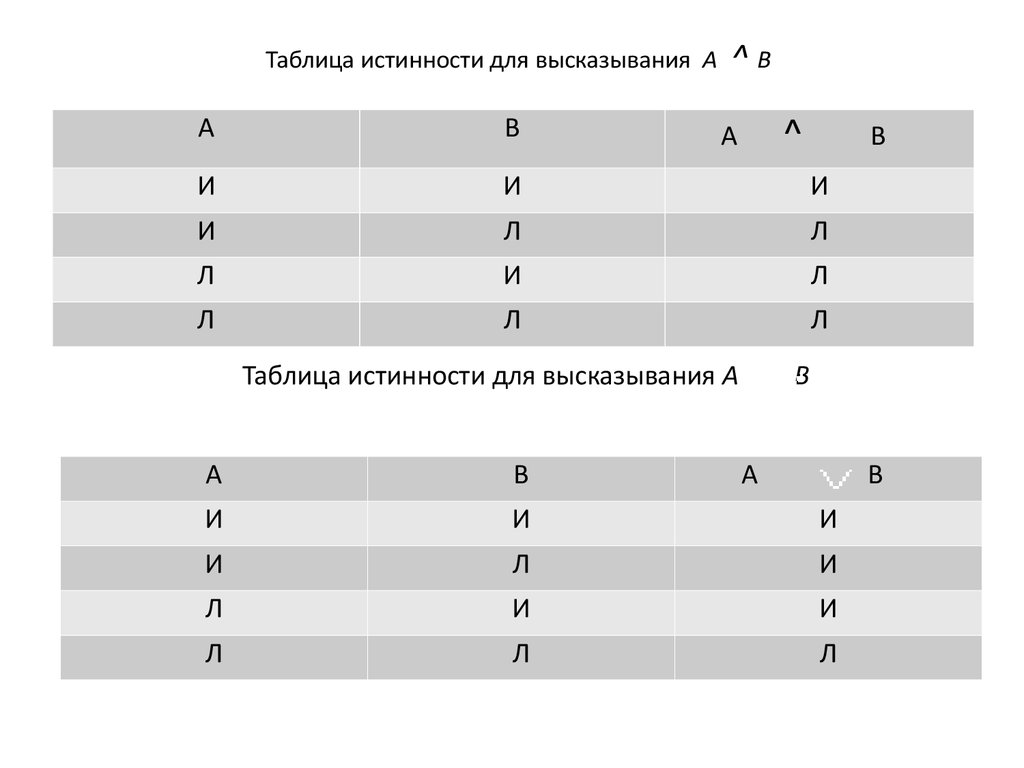
9. Таблица истинности для высказывания А ^ В

Таблица истинности для высказывания А
^В
^
А
В
И
И
И
И
Л
Л
Л
И
Л
Л
Л
Л
А
Таблица истинности для высказывания А
В
В
А
В
А
В
И
И
И
И
Л
И
Л
И
И
Л
Л
Л

10. Отрицание

• Логическая операция, соответствующая
логической связке «не», называется
отрицанием.
• Высказывание «не А», истинное лишь в том
случае, когда высказывание А ложно и ложное
лишь в том случае, когда высказывание А
истинно, называется отрицанием А
и обозначается .
А
И
Л
Л
И

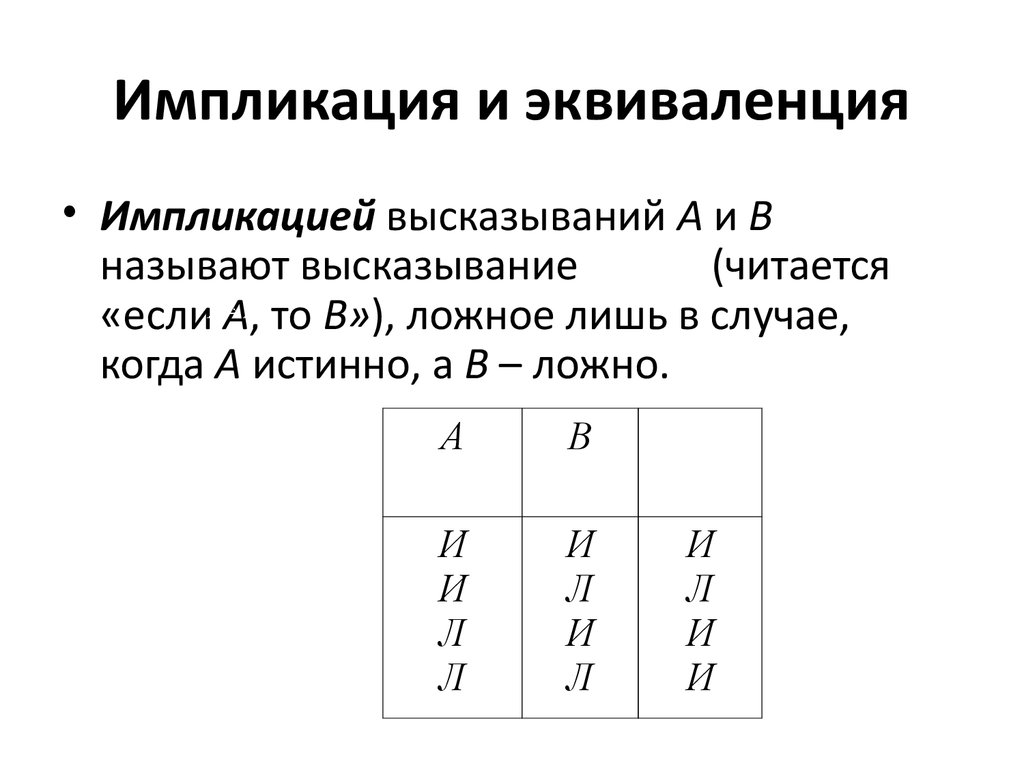
11. Импликация и эквиваленция

Импликация и эквиваленция
• Импликацией высказываний А и В
называют высказывание
(читается
«если А, то В»), ложное лишь в случае,
когда А истинно, а В – ложно.
А
В
И
И
Л
Л
И
Л
И
Л
И
Л
И
И

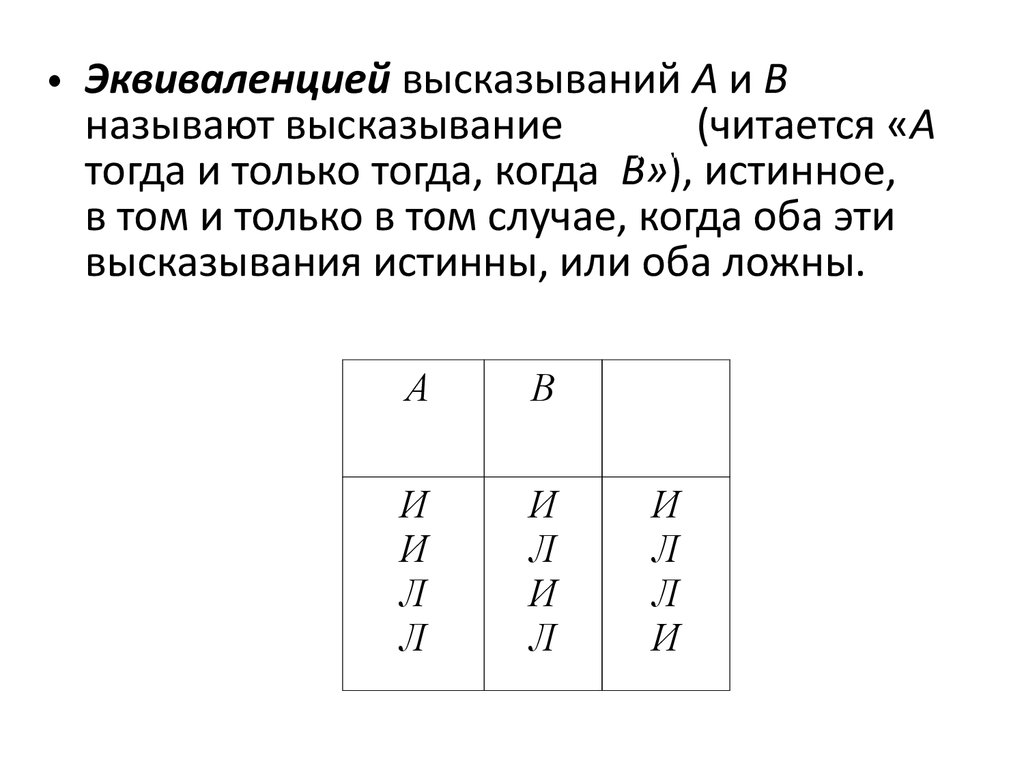
12.

• Эквиваленцией высказываний А и В
называют высказывание
(читается «А
тогда и только тогда, когда В»), истинное,
в том и только в том случае, когда оба эти
высказывания истинны, или оба ложны.
А
В
И
И
Л
Л
И
Л
И
Л
И
Л
Л
И

13. Язык и формулы логики высказываний        

Язык и формулы логики высказываний
Раздел математической логики, в котором изучают
свойства выражений, составленных из высказываний
с помощью логических операций, называется алгеброй
высказываний.
• Пусть X, Y, Z– переменные, обозначающие
элементарные логические высказывания или
их значения истинности. Такие переменные будем
называть логическими переменными.
• С помощью логических переменных и символов
логических операций можно формализовать любое
логическое высказывание. Таким образом, логическое
высказывание заменяется формулой, отражающей
логическую структуру этого высказывания.
• Например, высказывание «Число а делится на 6 тогда
и только тогда, когда а делится на 2, и а делится на 3»
формализуется в виде
.

14. Определим алфавит, то есть, набор символов, которые употребляются в логике высказываний:

Определим алфавит, то есть, набор символов,
которые употребляются в логике высказываний:
1.
(i – индекс, значения которого –
натуральные числа) – символы для обозначения
логических переменных,
2. И, Л – символы, обозначающие логические
константы «истина», «ложь»,
3.
- символы логических операций,
4. ( , ) – скобки, вспомогательные символы,
служащие для указания порядка выполнения
логических операций.

15. Определение формулы  логики высказываний:

Определение формулы логики
высказываний:
1.Всякая логическая переменная есть формула.
2. Символы И, Л есть формулы.
3. Если есть формула, то
есть формула.
4. Если
есть формулы, то
,
,
,
есть формулы.
5. Никаких других формул в логике
высказываний нет.

16. Алгоритм формализации высказываний.

• Если высказывание – простое, то ему ставится
в соответствие элементарная формула.
• Если высказывание – составное, то для
составления формулы требуется:
а) выделить все элементарные высказывания
и логические связки, образующие данное
высказывание,
в) заменить их соответствующими символами,
с) расставить скобки в соответствии со смыслом
данного высказывания.

17. Пример

Формализовать высказывание:
«Неверно, что число 500 делится на
3 или на 13»
Пусть X – « число 500 делится на 3»,
Y – «число 500 делится на 13».
Тогда данное сложное высказывание
имеет вид

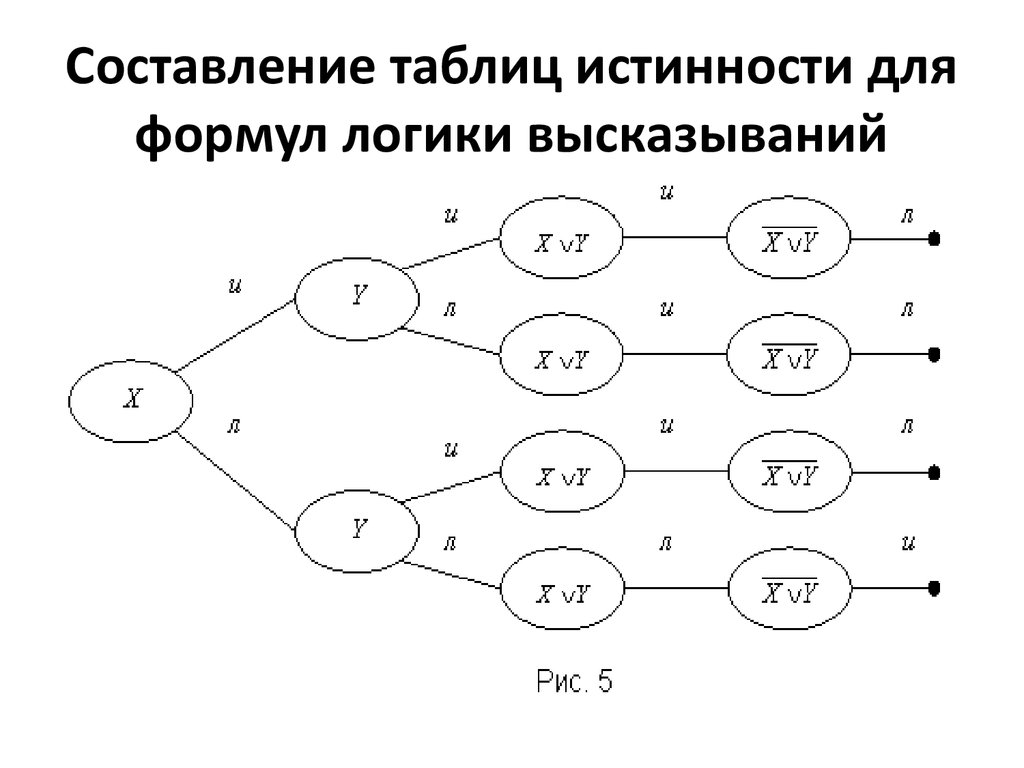
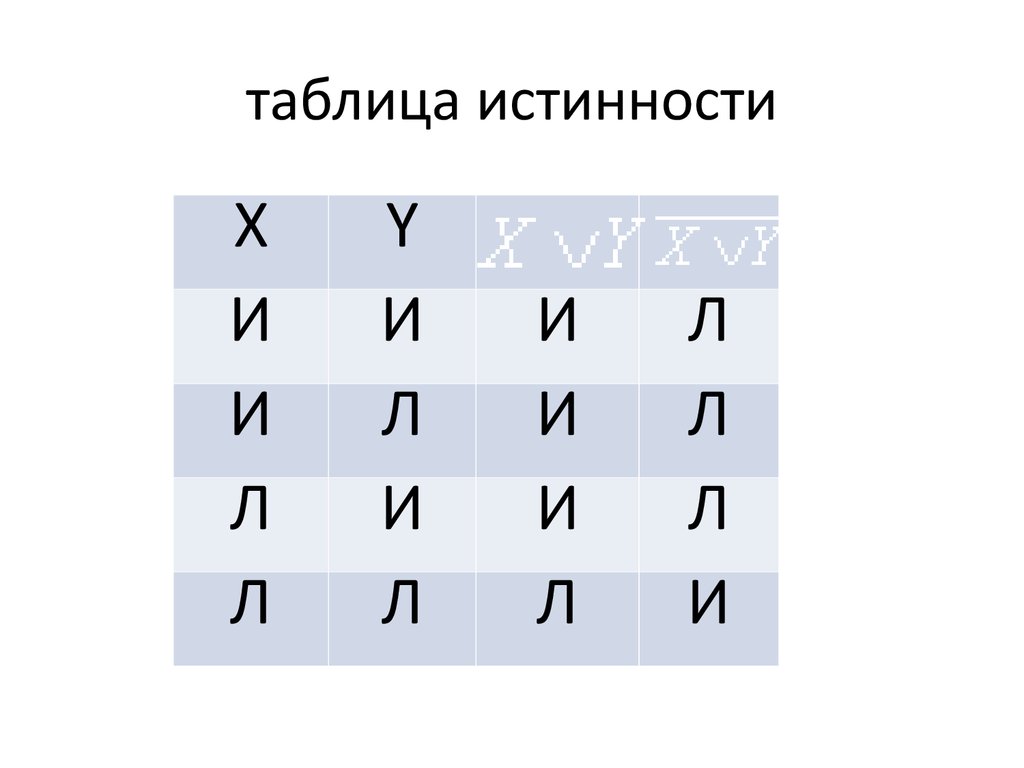
18. Составление таблиц истинности для формул логики высказываний

19. таблица истинности

X
И
И
Л
Л
Y
И
Л
И
Л
И
И
И
Л
Л
Л
Л
И

20. Логические функции Excel

Логическая функция ЕСЛИ имеет вид:
ЕСЛИ(x1; x2; x3),
где x1, x2, x3 – аргументы
x1 - логическое выражение,
x2, x3 – любые выражения, разрешенные в Excel;
причем вычисляется x2, если x1 имеет значение ИСТИНА, и x3, если x1
имеет значение ЛОЖЬ.
Если третий аргумент функции не определен, то ошибки в записи функции
нет – в этом случае ей присваивается значение ЛОЖЬ, если условие не
выполнено. Если ничего не нужно вычислять при невыполнении
условия, следует в качестве третьего аргумента задать пробел как текст.
Примеры: ЕСЛИ(A5>0;LN(A5);-1);
ЕСЛИ(B2<>0;1/B2;” ”)

21.

Логическая функция И имеет вид: - И(x1; x2;; …;xn), где x1; x2;; …;xn –
аргументы, являющиеся логическими выражениями.
Функция может содержать до 30 аргументов.
Функция И принимает значение ИСТИНА, если все ее аргументы
истинны, в противном случае она принимает значение ЛОЖЬ.
Функция может применяться для задания сложного условия,
определяемого системой равенств и неравенств:
x1
x2
...
xn
или, в форме логических
высказываний,
x1 - истинно?
x 2 - истинно?
...
xn - истинно?,
где xi – равенство или неравенство, которое может быть истинным
или ложным.

22.

• Логическая функция НЕ имеет вид - НЕ(x),
где x – логическое выражение. Ее значение
ИСТИНА, если x имеет значение ЛОЖЬ, и
наоборот.

23.

Логическая функция ИЛИ имеет вид:
ИЛИ(x1; x2, …;xn),
где x1; x2;; …;xn –аргументы, являющиеся логическими выражениями.
• Функция может содержать до 30 аргументов.
• Функция ИЛИ принимает значение ИСТИНА, если хотя бы один из ее
аргументов есть ИСТИНА, в противном случае она принимает
значение ЛОЖЬ.
• Функция применяется для задания сложного условия определяемого
совокупностью неравенств
x1
x2
...
xn
или
x1 - истинно?
x 2 - истинно?
...
xn - истинно?
где xi – равенство или неравенство, которое может быть истинным
или ложным.