Similar presentations:
Непрерывные реакторы для гомогенных гомофазных процессов
1.
Непрерывныереакторы для
гомогенных
гомофазных процессов.
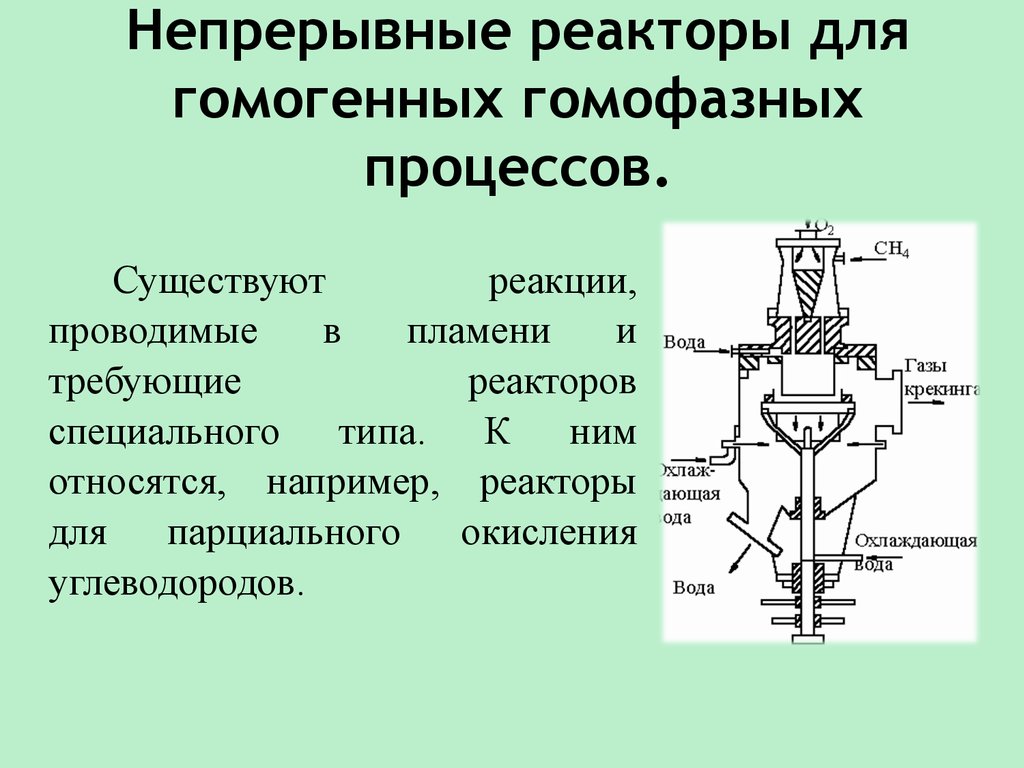
2. Непрерывные реакторы для гомогенных гомофазных процессов.
Существуютреакции,
проводимые
в
пламени
и
требующие
реакторов
специального типа. К ним
относятся, например, реакторы
для
парциального
окисления
углеводородов.
3.
Конструкционные особенности непрерывных реакторовдля гомогенных гомофазных процессов, в наибольшей
мере зависят от способа организации теплообмена. Это, в
первую очередь, касается газофазных фракций.
Относительно низкотемпературные жидкофазные реакции
чаще всего реализуются в политропических реакторах,
имеющих поверхность теплопередачи с хладоагентом
(теплоноситель). В реакторах вытеснения обмен теплот
осуществляется через поверхность трубы или пучка труб,
внутри которых двигается реакционная смесь, а с внешней
стороны – хладоагент (теплоноситель). Жидкофазные
реакторы смешения снабжены рубашками, встроенными
или выносными теплообменниками.
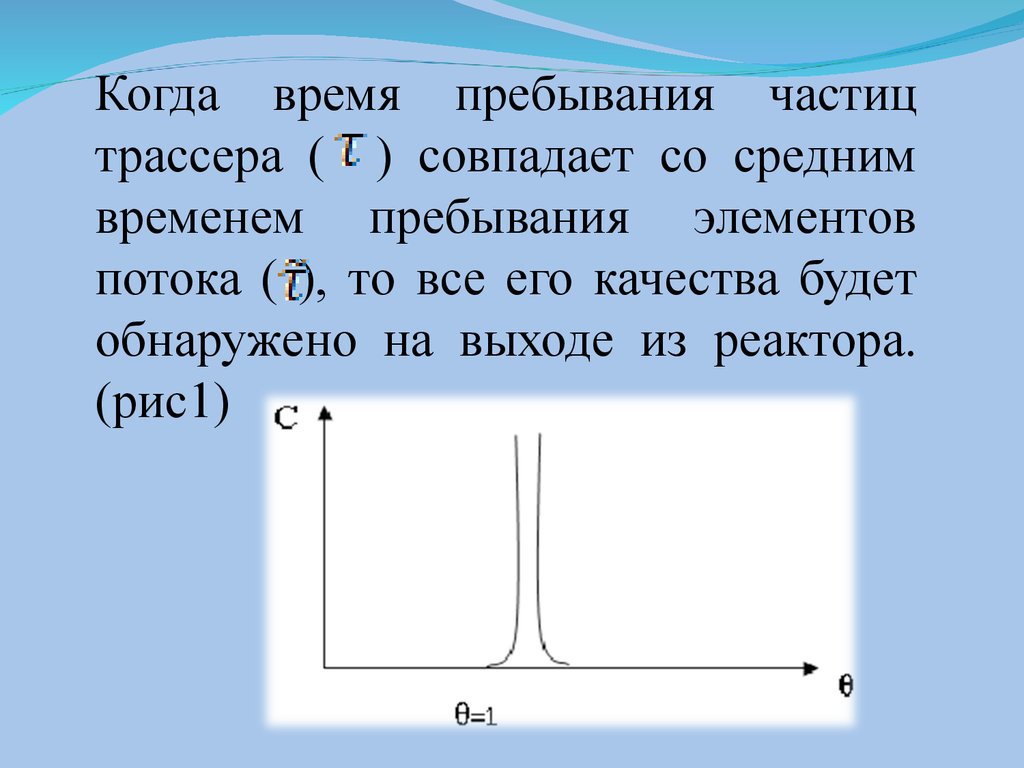
4.
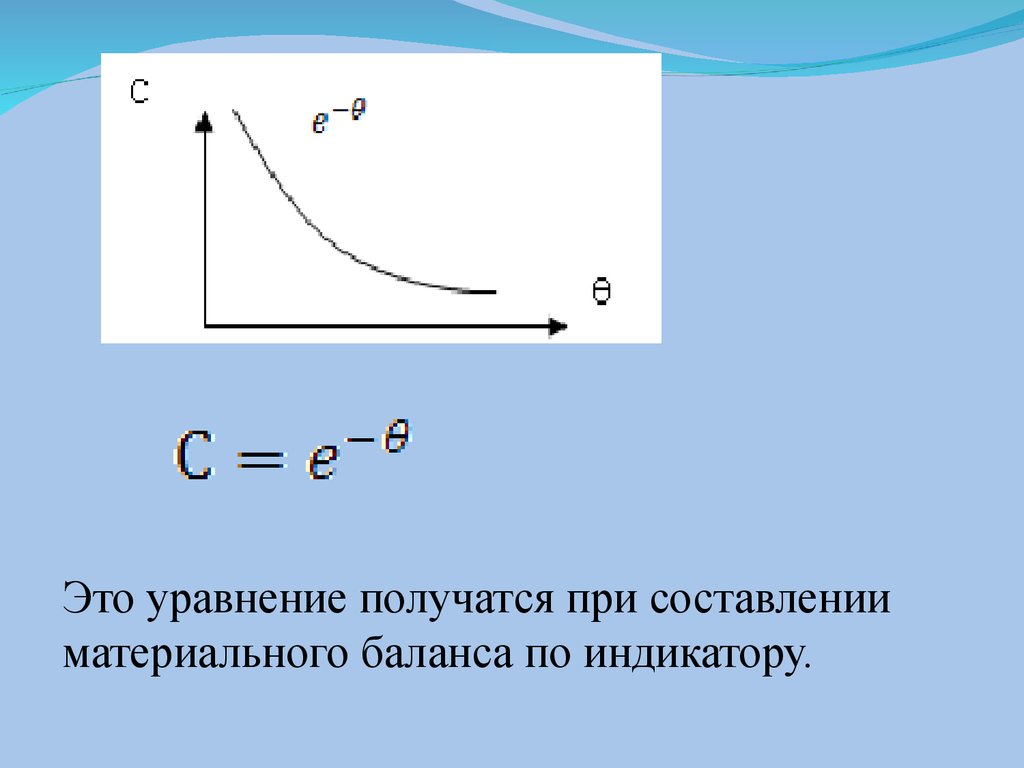
Длягазофазных
гомогенных
реакций
широко
распространены и политропический и адиабатический
режимы.
В адиабатических условиях тепло в реактор может
вводиться:
− С водяным паром
− С горючими газами
− С предварительно нагретым твердым мелкозернистым
инертным теплоносителем, который движется в
реакционном пространстве вместе с потоком реагентов.
5.
Вслучае
экзотермических
процессов реактор обычно имеет
керамическую насадку, которая
аккумулирует тепло, благодаря
чему при подаче холодной
реакционной смеси реакция не
затухает.
6.
Иногда реактор представляет собойпоследовательность отдельных адиабатических
секций, соединенных последовательно. В
промежутках между этими секциями возможно
организация теплообмена через поверхность
или путем введения в реакционную смесь
инертных
разбавителей
или
исходных
реагентов.
Если в первом случае
происходит только изменение температуры, то
во втором – также и состава, что должно
учитываться при соответствующих расчетах.
7.
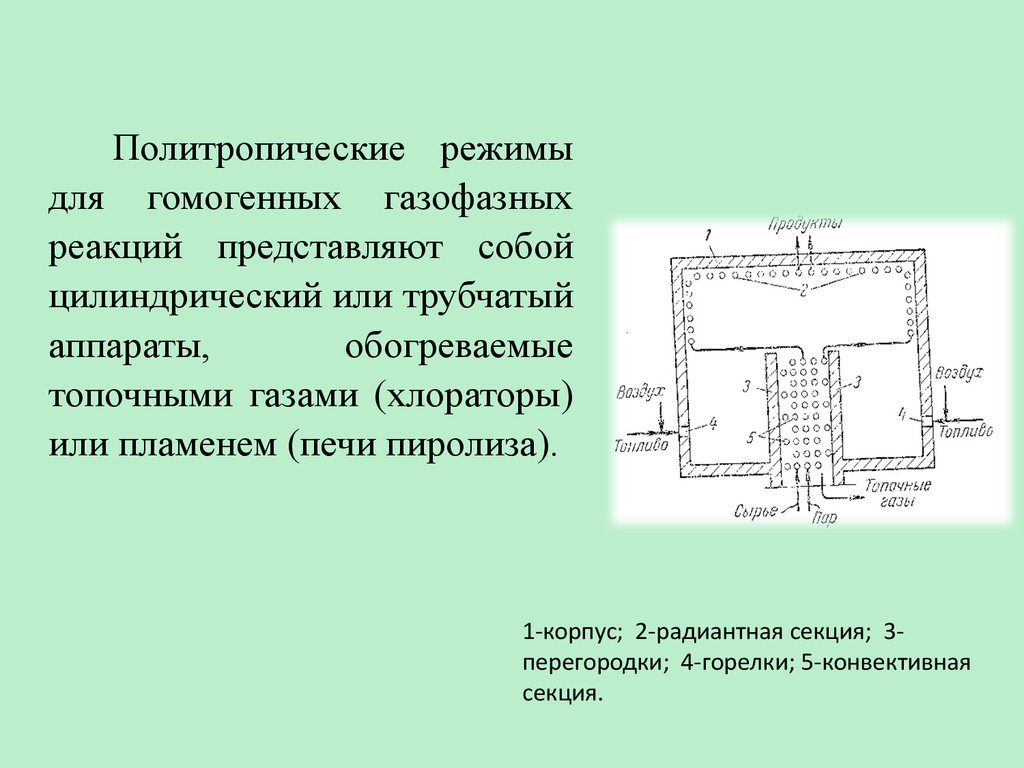
Политропические режимыдля гомогенных газофазных
реакций представляют собой
цилиндрический или трубчатый
аппараты,
обогреваемые
топочными газами (хлораторы)
или пламенем (печи пиролиза).
1-корпус; 2-радиантная секция; 3перегородки; 4-горелки; 5-конвективная
секция.
8.
Расчет непрерывныхидеальных,
изотермических
гомогенных
гомофазных реакторов.
9.
Расчет непрерывных реакторов, как и периодическихосуществляется
с
использованием
соответствующих
характеристических уравнений.
Исходными данными для расчета служат:
• Производительность по целевому продукту
• Степень превращения реагента ХА
• Начальные
концентрации
реагентов,
разбавителей, гомогенных катализаторов. СА0
инертных
10.
Визотермических
условиях
для
определения объема реактора достаточно
решения
характеристического
уравнения,
полученного при составлении материального
баланса только по определенному реагенту
А.
11.
Если возникает задача нахождениясостава реакционной смеси на выходе
из реактора, то в этом случае число
уравнений
возрастает
до
ключевых реагентов в системе.
FB =
числа
12.
Переход от FB к FA0 проводится по известным уравнениям сиспользованием ХА для простых или ХА и ФB для сложных
реакций. После определения FA0 объем реактора будет являться
уже только функцией параметра, характеризующей глубину
протекания реакций, например ХА .
Следует отметить, что это справедливо для всех
жидкофазных, а так же газофазных реакций, если перепадом
давления в реакторе от его входа до выхода можно пренебречь.
13.
Вобщем
случае
прохождение газового потока
через
реактор
может
сопровождаться
заметными
потерями давления.
Методика расчета потери
давления
в
трубчатых
пустотелых реакторах та же, что
и в трубопроводах. В расчетах
принимают, что потеря давления
равно потерям при трении,
пренебрегая
остальными
составляющими
уравнения
баланса механической энергии.
14. Где: P – общее давление в реакторе λ- коэффициент трения -плотность реакционной массы - линейная скорость потока - эквивалентный диаметр кан
Тогда для элементарной длинны реактораможно записать:
Где: P – общее давление в реакторе
λ- коэффициент трения
-плотность реакционной массы
- линейная скорость потока
- эквивалентный диаметр канала, по которому
Для ламинарного потока
движется поток (для труб крупного сечения ).
15.
Притурбулентном
находятся
пути
экспериментальных
движении
обработки
данных
с
использованием теории подобия и
является функцией числа Re
шероховатости стенок труб.
и
16.
Дифференциальное уравнение падениядавления можно проинтегрировать, если
известно, каким образом будет меняться Л, w
и p по длине реактора, в котором протекает
химическая реакция. Факторами, влияющие
на величину Л, w и p является температура и
состав реакционной смеси, последний из
которых будет определяющим.
17.
Представимлинейную
скорость
потока и его плотность как функцию
параметра, характеризующего глубину
протекания реакции, в качестве которого
выберем степень превращения реагента
А:
ε- коэффициент изменения объема.
18.
Если раздельно W и p изменяются приизменении ХА, то их произведение остается
постоянной величиной, равной Wopo .
Очевидно, что если считать m не зависит от
состава реакционной смеси, что достаточно
справедливо для газовой фазы, то число Re,
а также λ не изменяются при увеличении
ХА.
19.
Теперь можно записать:Для оценочных расчетов падение давления как функции длинны
реактора можно заменить 1+εХА на её среднеарифметическое значение
при ХА=0, ХА=ХАLТогда:
Где ΔР– падение давления в реакторе длиной
Объем раствора:
n-число труб круглого сечения в реакторе
20.
При точных расчетах уравнение падениядавления
необходимо
рассматривать
совместно
с
характеристическим
уравнением
реактора
идеального
вытеснения.
n-число
труб
21.
Объединяя уравнение получим:22.
ЗависимостьР
от
L
находится при совместном
решении характеристического
уравнения
и
уравнения
учитывающего
падение
давления, как функцию ХА.
Одновременно
с
этим
определяется объем реактора.
23.
24.
Основные моделиреальных изотермических
гомогенных реакторов
25. Основные модели реальных изотермических гомогенных реакторов
Для реальных моделей введено понятие:«распределение времени пребывания элементов
потока».
Часто проводя изучение времени пребывания
элементов потока на «холодных», имеющие основные
размеры моделируемых аппаратов. Для этого
применяют метод, основанный на искусственном
нанесении возмущения на систему и анализе отклика
на него системы. Под системой подразумевается
непрерывно работающий реактор (или его «холодная»
модель), а под возмущением – введенный тем или
иным способом в поток индикатор (трассер).
26.
Отклик на возмущение представляетсяв виде кривых зависимости концентрации
трассера от времени, которая называется
кривыми или функциями отклика. При
соответствующей обработке этих кривых
получают функцию распределения времени
пребывания элементов потока в реакторе.
27.
Наиболее распространены два следующихспособа введения трассера в реактор. В первом
случае в поток, поступающий в аппарат и не
содержащий трассирующего вещества, вводится
некоторое количество индикатора и затем его
концентрация постоянно поддерживается на входе в
реактор на одном и там же уровне. Во втором случае
индикатор вводится в поток одноразово в виде
импульса, как например, проба в газожидкостный
хроматограф.
Последний
способ
наиболее
распространен. В этом случае выходную кривую
называют С-кривой, а импульсный выходной сигнал
– дельта функцией или функцией Дарка.
28.
Частовыходные
кривые
представляют
в
безразмерных
координатах.
По
оси
ординат
откладывается
безразмерная
концентрация трассера С=с/С0, c текущая концентрация трассера на
выходе из реактора, С0 - начальная
концентрация трассера в реакторе,
определяемая в виде: М0/V, где – М0
начальное количество молей трассера.
29.
Пооси
абсцисс
безразмерное время
, где
откладывается
– текущее время,
– среднее время пребывания элементов
потока в реакторе, определяемое из
соотношения
где W– объемная скорость потока
неизменной плотности.
30.
Зависимость cдифференциальной,
от
а зависимость
от
–
интегральной
распределения.
называется
функциями
31.
Рассмотрим вид кривых откликареакторов идеального вытеснения
и смешения при нанесении
импульсного
возмущения.
Введенный трассер в виде тонкой
пленки
равномерно
распределяется на входе по всему
сечению реактора идеального
вытеснения и в «поршневом»
режиме, не размываясь, движется
к выходу.
32.
Свойство С-кривой таково, чтоТеоретически импульсный ввод
определенного количества трассера
осуществляется за бесконечно малый
промежуток времени. Учитывая эти два
обстоятельства, кривая отклика для
реактора
идеального
вытеснения
выражается прямой, уходящей в
бесконечность.
33.
Когда время пребывания частицтрассера ( ) совпадает со средним
временем пребывания элементов
потока ( ), то все его качества будет
обнаружено на выходе из реактора.
(рис1)
34.
В реакторе идеального смешенияколичество трассера, введенного
импульсно (мгновенно), т.е. за время
много меньше, чем среднее время
пребывания,
перемешивается
с
содержимым
реакционного
пространства.
Затем
происходит
«вымывание» индикатора уходящим
из реактора потоком, согласно закону
(рис2).
35.
Это уравнение получатся при составленииматериального баланса по индикатору.
36.
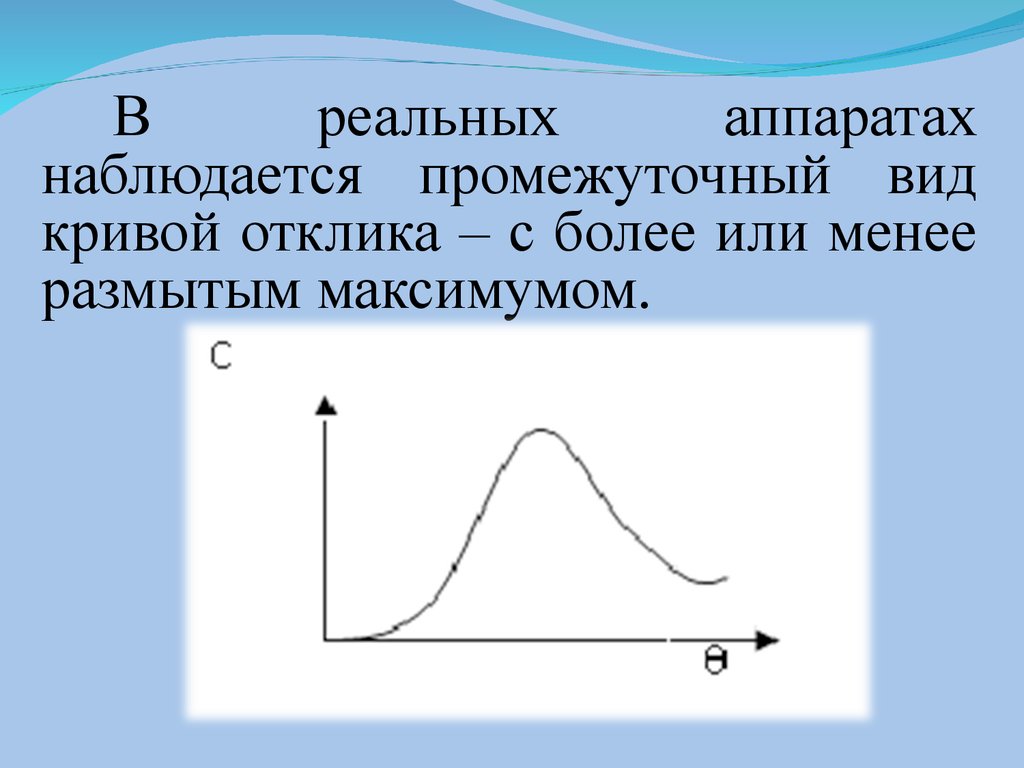
Вреальных
аппаратах
наблюдается промежуточный вид
кривой отклика – с более или менее
размытым максимумом.
37.
Очевидно, что время пребыванияэлементов потока в реакторе является
случайной величиной. Её функцию
распределения
(кривую
отклика)
относительно просто охарактеризовать
некоторыми
величинами,
которые
называются моментами распределения
случайной
величины.
Или
можно
пользоваться
для
сопоставления
распределений
без
сравнения
соответствующих кривых. Наибольшее
значение и применимость имеют первые
два момента: среднее значение и
дисперсия распределения.
38.
Кривые отклика чаще всего строят поточкам,
в
которых
бывает
известна
концентрация трассера нВ выходе из реактора в
определенный момент времени – время отбора
пробы. В этом случае среднее время
пребывания определяется по формуле:
среднее время пребывания
-концентрация трассера в –пробе
-время отбора пробы.
39.
Дисперсия распределения временипребывания может быть рассчитана по
уравнению:
40. Причины отклонения от идеальности проточных реакторов
41. Причины отклонения от идеальности проточных реакторов
Время пребывания отдельных элементовпотока в проточном реакторе – это
случайная величина которая меняется
значительно от 0 до ∞.
Застойная зона. (часть потока не
принимают участия в реакции)
42. Причины отклонения от идеальности проточных реакторов
1) Наличие внутренних байпасов2) Зоны циркуляции.
43.
В реальных реакторах, даже близких креактору
идеального
вытеснения
может
происходить частичное перемешивание элементов
потока в основном направлении. Это может
возникнуть в результате молекулярной диффузии:
в двух точках потока концентрации разные, в
результате – движущая сила диффузии.
Наряду с молекулярной диффузией –
турбулентная диффузия – хаотичное пульсации
скорости относительно среднего значения в
продольном направлении. Диффузия в осевом
направлении
происходит
в
следствии
неравномерности поля скоростей (при ламинарном
течении жидкости).
44. Модели, учитывающие неидеальность потока, упрощающие расчет реактора
Ячеечная модель – реальный аппарат расчленяютна N последовательно соединенных ячеек идеального
смешения. Суммарный объем всех ячеек равен
полному объему реактора.
Число ячеек
ячеечной модели.
N
–
единственный
параметр
Диффузионная
модель
–
некоторый
промежуточный случай между режимами идеального
смешения и идеального вытеснения. Учет диффузии
в соответствии с первым законом Фика.
45.
Коэффициент продольной диффузии - DL - единственныйпараметр
однопараметрической
дифференциальной
модели.
В теории реакторов разработаны модели позволяющие
учесть неидеальность потока. Модели эти являются до
некоторой степени приближенными, однако они более
точно описывают реальный процесс.
46.
Модели реальных реакторов могут быть построены на основе двухподходов:
1. Первый основан на мысленной замене реактора реального той или
иной комбинацией идеальных аппаратов.
2. Второй подход имеет большее физическое обоснование – при
составлении материального описания процесса стремятся учесть все
реальные физические явления, происходящие в аппарате и внести их
в уравнение с помощью соответствующих математических
операторов.
47.
При разработке модели необходимо иметь в виду, что, какправило, теория дает общий вид уравнения, а численные
коэффициенты этих уравнений должны быть найдены
экспериментально. Эти численные коэффициенты носят
название параметров математической модели. Стремятся,
чтобы число параметров было минимальным.
Наиболее
распространены
2
модели
однопараметрические: ячеечная и диффузионная.
48. Ячеечная модель.
Модуль потока с продольным перемешиванием можнопредставить в виде КРПС. В ячеечной модели использован
первый подход к описанию реальных реакторов, а именно:
реальный
аппарат
мысленно
расщепляют
на
N
последовательно соединенных ячеек идеального смешения.
Суммарный объем всех ячеек равен полному объему
реактора. Правомерность такой замены вытекает из сравнения
КРПС с РИВ и РПС.
N=1 РИВ
N=∞ для реального реактора.
49. Однопараметрическая диффузионная модель
50.
Диффузионная модель, как и ячеечная,описывает
реальную
гидродинамическую
обстановку в проточном реакторе как некоторый
промежуточный случай между режимами
идеального смешения и идеального вытеснения.
При
построении
диффузионной
модели
идеального
смешения
учитывается
неравномерность распределения параметров
процесса С/V (в частности, концентрации) по
объему аппарата.
51.
Нонеравномерным
является
и
распределение
концентрации
по
длине
реактора идеального вытеснения. В отличие от
модели
идеального
вытеснения
в
диффузионной модели учитывается наличие
перемешивания реакционной среды в осевом
направлении, вызванное различными видами
диффузии. Последнее условие и легло в основу
названия модели – диффузионная.
52.
Учет диффузии связан с появлением вматематическом
уравнении
дифференциальных уравнений, т.к. с
первым законом Фика перенос вещества
(изменение его количества в элементарном
объеме) за счет диффузии пропорционален
градиенту концентрации в направлении
переноса.
53. Однопараметрическая диффузионная модель
Вреальном
аппарате
в
связи
с
Однопараметрическая
неравномерностью распределения концентрации в
пространстве имеет место диффузионный
перенос
диффузионная
модель
как в продольном, так и радиальном направлении.
Чтобы
чрезмерно
не
усложнять
математическое описание в первом приближении
считают, что в радиальном направлении
распределение концентрации равномерное и
диффузия имеет место только в продольном
(осевом направлении).
54.
Перенос вещества за счет турбулентнойдиффузии Dтруб. Но разделить экспериментально
различные виды диффузии сложно, поэтому
целесообразно все их объединить одним уравнением с
коэффициентом продольной диффузии DL - это
единственный
параметр
однопараметрической
диффузионной модели.
В первом приближении, если длинна
реактора больше его диаметра в 50÷60 раз, то
отклонением от режима идеального вытеснения,
вызванным продольной турбулентной диффузией,
можно принебречь.
55.
Диффузионные модели,их характеристики.
56.
Под диффузие будет пониматься переносчасти жидкости или газа под влиянием градиента
концентрации, независисмо от механизма этого
переноса. Следовательно, в общем случае это
может быть молекулярная и турбулентная
диффузия;
перемешивание,
вызванное
пульсацией потока и насадкой, если такая
имеется, конвективный перенос причиной
которого могут быть градиенты температуры и
т.д.
57.
Рассмотрим вначале модель, в которой учитываетсявлияние продольной диффузии на режим идеального
вытеснения. Такая модель используется для описания
работы трубчатых аппаратов, подразумевая отсутствие а
них застойных зон и струйных потоков.
58.
Как и процесс молекулярной диффузии, осевое смешение в силу его статистическойприроды описывается уравнением, анологичным по виду закона Фика. Однако в нем вместо
коэффициента молекулярной диффузии используется эффективный коэффициент
продольного переноса DL, полностью характеризующий степень осевого смешения в потоке.
Коэффициент DL является функцией длинны реактора, но в технических расчетах
используется его среднее значение DL.
59.
Рассмотрим реактор длинной L, в котором движется установившийся(стационарный во времени) поток с осевым перемешиванием веществ.
Запишем для элементарного объема реактора уравнение материального
баланса. (повторить РИВ).
60.
Если в реакторе идеального вытеснения существует только один конвективный поток, тотеперь добавляется ещё и осевое диффузионный поток. Очевидно, в этом случае
характеристическое уравнение будет отличаться от полученного для реактора идеального
вытеснения на некоторое слагаемое, учитывающее вклад продольного перемешивания:
DL – эффективный коэффициент продольного переноса.
61.
Проведем некоторые преобразования этого уравнения, облегчающее его дальнейшее решение:Окончательно имеем:
w - линейная скорость потока.
62.
В случае жидкофазных реакций линейная скорость потока практически не меняется по длинереактора и поэтому может быть вынесена из-под знака дифференциала. Для газофазных
реакций, протекающих с изменением объема в технологических расчетах часто используют
среднее значение w, легко определяемого для известной конечной степени превращения
ключевого реагента А. Тогда:
63.
Решение уравнения возможно, если известны начальные условия. При l=0, учитывая непрерывность переноса А, получим:Для конечной величины DL это условие влечет за собой прерывистое уменьшение начальной концентрации А при L=0.
Другим условием является
=0 при l=L
64.
Введем следующие обозначения:Теперь можно записать
(при z=0)
(при z=1)
65.
Аналитическое решение этой системы уравнений возможно только в отдельных случаях, например, дляреакции первого порядка. В этом случае решение имеет вид:
Полученный результат справедлив для любых значений критерия Пекле (
).
66.
В предельных случаях (или
)
разлагая в ряд этот результат решения, получаем известные расчетные формулы реактора идеального вытеснения
и реактора идеального смешения
67.
Для более сложных кинетических закономерностей, чем реакция первогопорядка, применяют численные методы решения записанной ранее
системы уравнений.
Вообще её любое решение предполагает, что численное значение
критерия Пекле известно. Рассмотрим метода его нахождения.
68.
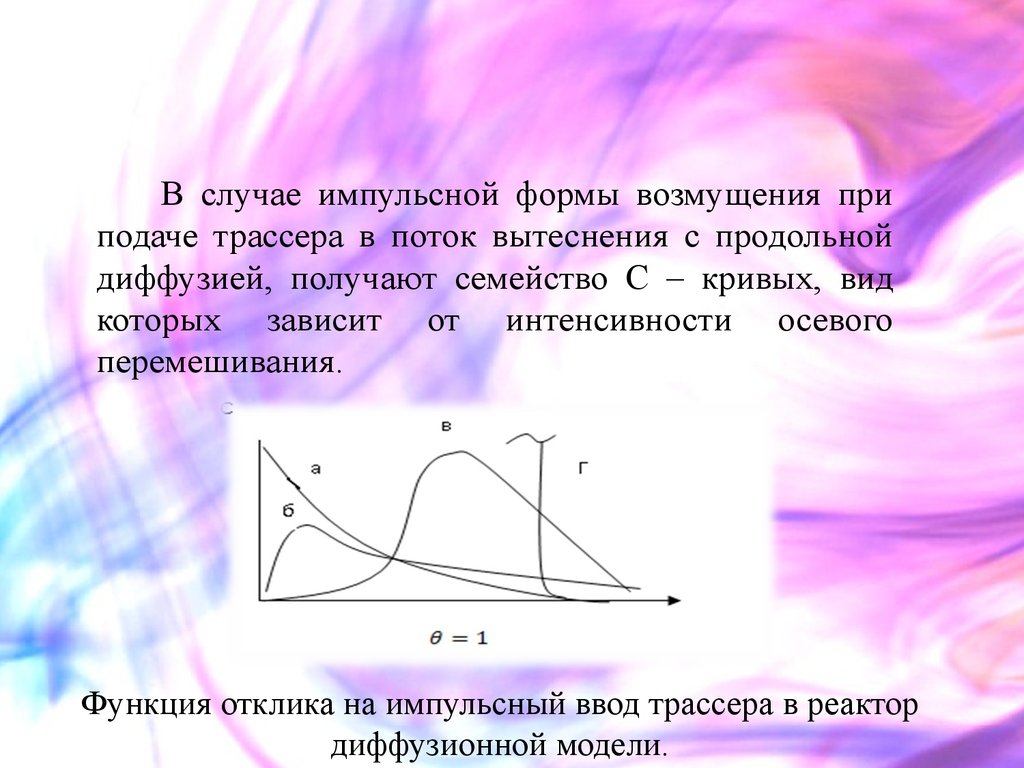
В случае импульсной формы возмущения приподаче трассера в поток вытеснения с продольной
диффузией, получают семейство С – кривых, вид
которых зависит от интенсивности осевого
перемешивания.
Функция отклика на импульсный ввод трассера в реактор
диффузионной модели.
69.
а)Найдена однозначная связь между дисперсией распределения и критерием PeL в зависимости от условий на границе аппаратов.
Различают «закрытые», «открытые», и «частично закрытые» типы аппаратов.
В «закрытых» реакторах ввод трассера осуществляется на входе в аппарат, а вывод - на выходе. В «открытых» реакторах ввод и вывод трассера
осуществляются на участках реакционной трубки, удаленном на некотором расстоянии от входа и выхода аппарата. «Полузакрытый» типы
аппаратов являются комбинацией первых двух.
70.
Во всех рассмотренных типах реакторов вытеснения зависимостьВид второго слагаемого меняется в зависимости от используемого типа реактора. Однако, чаще всего его вклад по
сравнению с первым слагаемым мал, поэтому в технических расчетах пользуются соотношением:
71.
Величина критерия Пекле может быть найдена по критериальным зависимостям, которыеимеются в специальной литературе. Критериальные зависимости получены при
экспериментах на лабораторных установках менее надежны, чем определение критерия Пекле
на «холодных» моделях.
72.
Нахождение объема реактора для заданной производительности по целевом продукту ВВ случае простых реакций, когда ФВ=1, учитывая стехиометрические коэффициенты реакции и конечную степень
превращения реагента А, переходят от FB и FA0 затем, зная СА о к W. Выбирают сечение трубrи реактора S и затем
принимают такое их количество n, чтобы в трубках создавался нужный гидродинамический режим. Затем находят
w=W/nS и PeL критерий Пекле при этой линейной скорости потока. Задаются некоторой длиной реактора L и
определяют r=L/w.
Полученное значение w, PeL, r используется для расчета САL при численном решений рассмотренной ранее системы
уравнений. Полученное значение С АL сравнивают с заданной величиной С А, и если они совпадают, то задача решена. В
противном случае решение повторяют при другом выбранном значения длинны реактора.
73.
Обратное перемешивание уменьшает удельную производительность реактора. Для сложных реакций от распределениявремени пребывания зависит не только удельная производительность, но и селективность. Это особенно существенно в случае
последовательных реакций, когда один из промежуточных продуктов – целевой. Величина максимальной селективности
снижается при возникновении продольного перемешивания тем более, чем оно интенсивнее. Поэтому в случае сложных реакций
при наличие в трубчатом реакторе осевого перемешивания интегральная селективность даже для изотермических условий не
может быть рассчитаны, исходя из фВ и ХА.
74.
В связи с этим методику расчета объема реактора с продольным перемешиванием для сложных реакций призаданной производительности по целевому продукту можно представить следующим образом.
Задаемся некоторым значением ФВ. Это позволяет как и для простых реакций найти w, PeL, r . Затем решатся такое
число характеристических уравнений, которое позволяет определить текущие концентрации веществ A и B в
реакторе.
75.
Например. Пусть имеется реакциядля которой
и
В данном примере необходимо решить совместно два характеристических уравнения с учетом их граничных условий.
76.
77.
Правильность выбора необходимой длинны реактора осуществляется так же, как и для простых реакций. В результате окончательногорасчета находят соответствующее значение. Затем проверяют по формуле:
Насколько совпадают принятые и рассчитанные значения интегральной селективности по целевому продукту В. Если совпадение ниже
требуемой точности, то расчет полностью повторяют при новом выбранном значении ФВ.





































































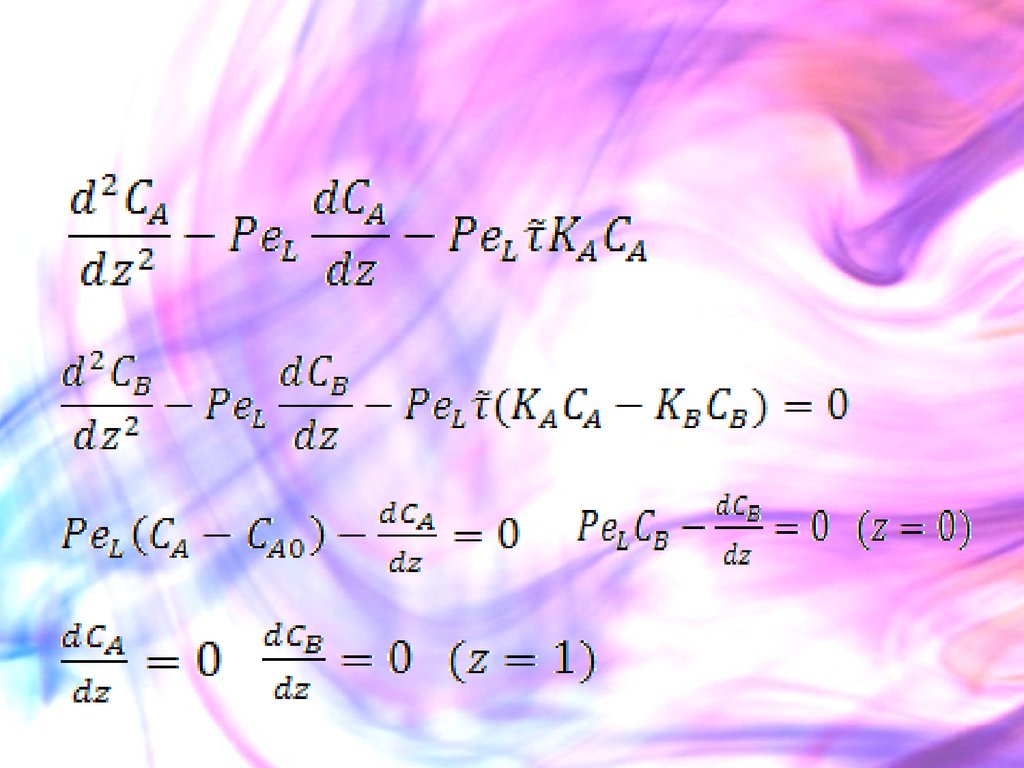

 physics
physics chemistry
chemistry industry
industry








