Similar presentations:
Признак перпендикулярности прямой и плоскости. 10 класс
1.
Математика10 класс
2.
Определение. Прямая называется перпендикулярной кплоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
a
S
A
N
D
F
H
a AS , a AF , a FS , a ND, a DH , a HN
3.
3.Признак перпендикулярности прямой и плоскости.Если прямая перпендикулярна к двум пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна к этой плоскости.
р
a
p
,a p,
q , a q,
a
4.
ПланиметрияСтереометрия
А
А
а
М
Н
М
Н
Отрезок АН – перпендикуляр
Точка Н – основание перпендикуляра
Отрезок АМ – наклонная
Точка М – основание наклонной
Отрезок МН – проекция
наклонной на прямую а
Отрезок МН – проекция
наклонной на плоскость
5.
ПланиметрияСтереометрия
А
А
а
М
Н
М
Н
Из всех расстояний от точки А до
плоскости
различных точек прямой
а
наименьшим является длина
перпендикуляра.
Расстояние от точки до
Расстояние от точки до
прямой – длина
плоскости – длина
перпендикуляра
перпендикуляра
6.
Расстояние от лампочки до землиизмеряется по перпендикуляру,
проведенному от лампочки к
плоскости земли
7.
Постановка проблемыДана плоскость .
Из точки А опущен перпендикуляр на плоскость .
В плоскости проведена прямая с .
Вопрос: 1.Как найти расстояние от точки В до прямой с?
2.Как найти расстояние от точки А до прямой с?
А
П-Р
В
Н-я
П-я
М
с
8.
АА
В
В
с
с
А
В
М
с
М
Прямая, проведенная в
плоскости через основание
наклонной, перпендикулярно к
ее проекции на эту плоскость,
перпендикулярна и
к самой наклонной.
9.
Прямая, проведенная в плоскости черезоснование наклонной перпендикулярно к
ее проекции на эту плоскость,
перпендикулярна и к самой наклонной.
Обратная теорема. Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
П-Р
Н-я
П-я
Н
М
a
10.
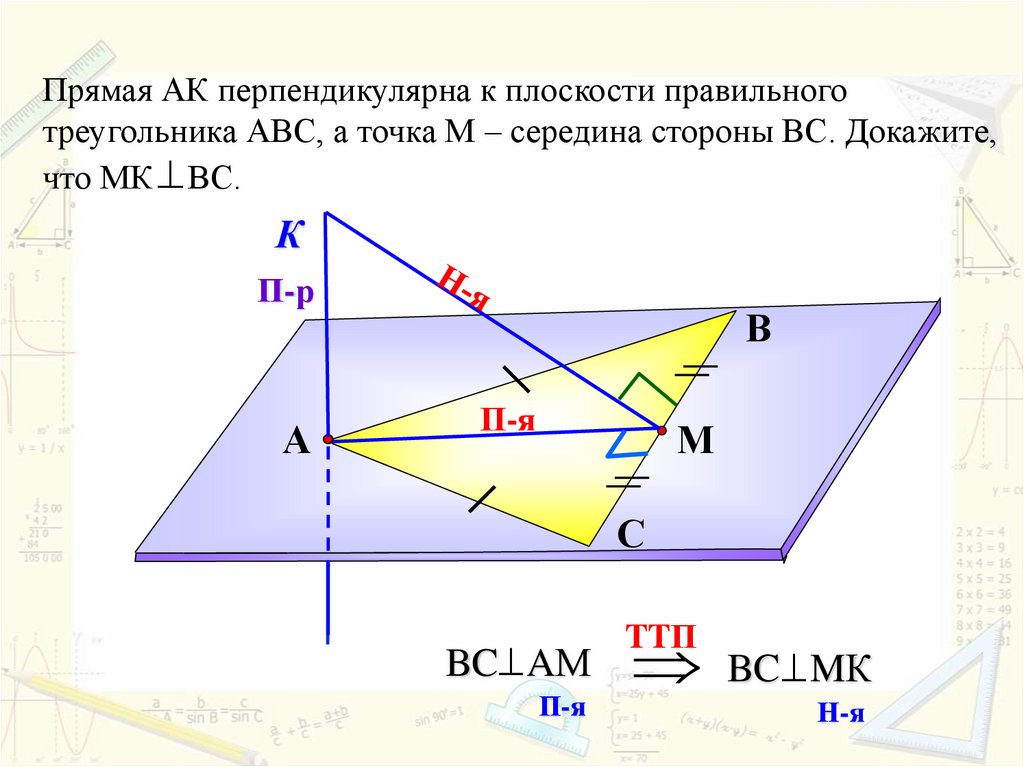
Прямая АК перпендикулярна к плоскости правильноготреугольника АВС, а точка М – середина стороны ВС. Докажите,
что МК ВС.
К
П-р
А
В
П-я
М
С
BC AМ
П-я
TTП
BC MК
Н-я
11.
Через вершину А прямоугольника АВСD проведена прямая АК,перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см,
КВ = 7 см, КС = 9 см. Найдите:
а) расстояние от точки К до плоскости прямоугольника АВСD;
б) расстояние между прямыми АК и СD.
K
КА – искомое расстояние
АD – общий перпендикуляр
АD – искомое расстояние
6
D
9
П-я 1
С
П-Р
?
А
Найдем другие прямые углы…
TTП
СD AD
П-я 1
7
BC BA
П-я 2
В
CD Н-яDK1
TTП
BC BK
Н-я 2
12.
Домашнее задание.П.15 изучить, № 15.2,15.4,
13.
№1.Через вершину прямого угла С равнобедренного прямоугольного
треугольника АВС проведена прямая СМ, перпендикулярная к его
плоскости. Найдите расстояние от точки М до прямой АВ, если
АС = 4 см, а СМ = 2 7 см.
М
П-р
2 7
С
А
4
П-я
F
В
AВ СF
П-я
TTП
AВ MF
МF – искомое расстояние
Н-я
14.
№2.Из точки М проведен перпендикуляр МВ к плоскости
прямоугольника АВСD. Докажите, что треугольники АМD и
МСD прямоугольные.
TTП
AD AB
М
П-я 1
DC BC
П-Р
А
П-я 1
D
П-я 2
В
С
AD AM
Н-я 1
TTП
DC CM
Н-я 2
15.
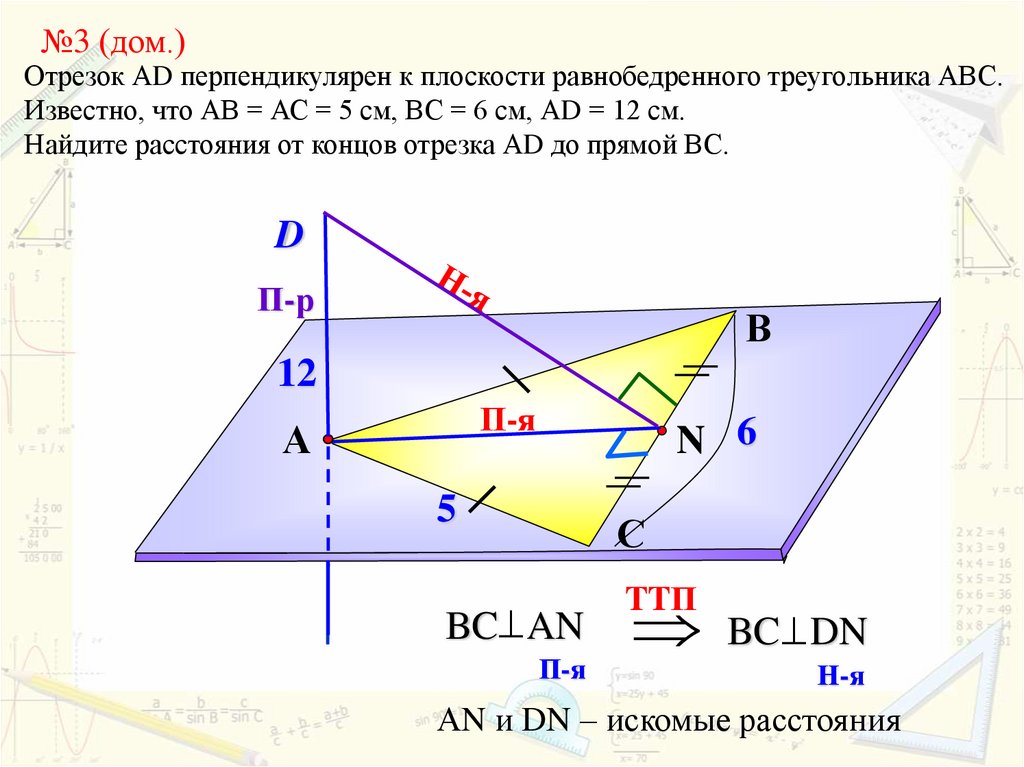
№3 (дом.)Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС.
Известно, что АВ = АС = 5 см, ВС = 6 см, АD = 12 см.
Найдите расстояния от концов отрезка АD до прямой ВС.
D
П-р
В
12
П-я
А
N 6
5
С
BC AN
П-я
TTП
BC DN
Н-я
АN и DN – искомые расстояния













 mathematics
mathematics








