Признак перпендикулярности прямой и плоскости

1.

Математика
Разработала учитель математики
высшей категории
МКОУ «Гимназия №14» г.о.Нальчик
Новохатько Марина Эдуардовна

2.

«Единственный путь,
ведущий к знаниям,- это
деятельность.»
Бернард Шоу

3.

Актуализация
знаний
1. Угол между прямыми равен 90˚. Как называются такие прямые?
Ответ: перпендикулярные.
2.
Дать определение прямой, перпендикулярной к плоскости:
Определение. Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
a
S
A
N
D
F
H
a AS , a AF , a FS , a ND, a DH , a HN

4.

3. Сформулировать Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна к двум пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна к этой плоскости.
р
a
p
,a p,
q , a q,
a

5.

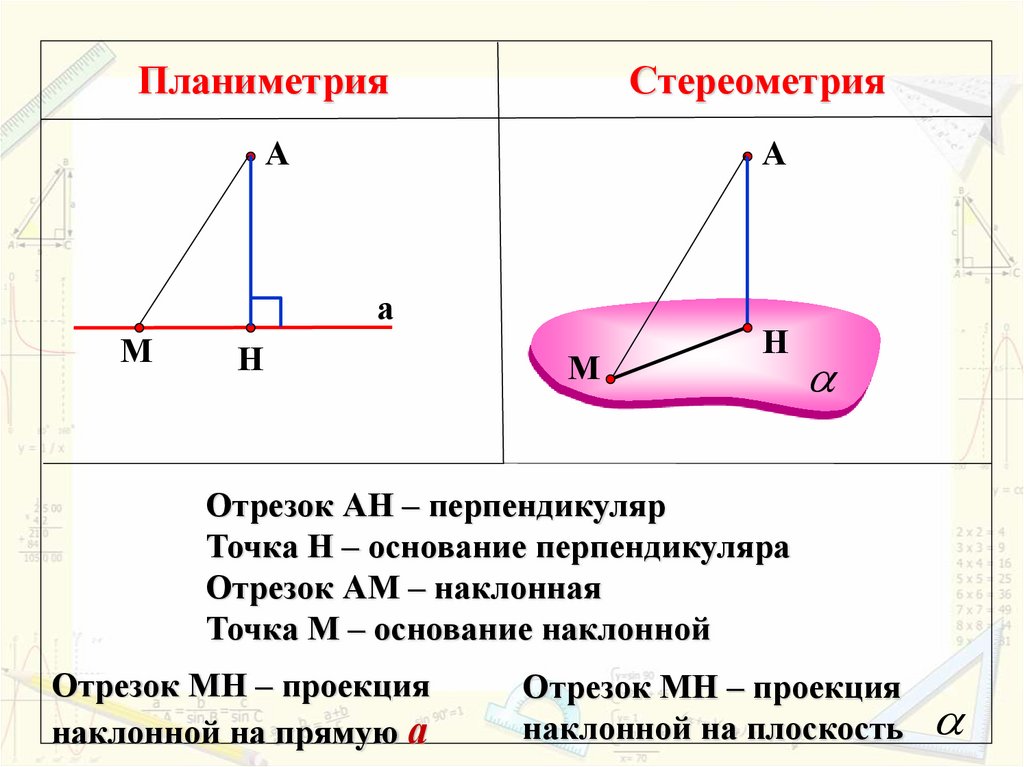
Планиметрия
Стереометрия
А
А
а
М
Н
М
Н
Отрезок АН – перпендикуляр
Точка Н – основание перпендикуляра
Отрезок АМ – наклонная
Точка М – основание наклонной
Отрезок МН – проекция
наклонной на прямую а
Отрезок МН – проекция
наклонной на плоскость

6.

Планиметрия
Стереометрия
А
А
а
М
Н
М
Н
Из всех расстояний от точки А до
плоскости
различных точек прямой
а
наименьшим является длина
перпендикуляра.
Расстояние от точки до
Расстояние от точки до
прямой – длина
плоскости – длина
перпендикуляра
перпендикуляра

7.

Расстояние от лампочки до земли
измеряется по перпендикуляру,
проведенному от лампочки к
плоскости земли

8.

Постановка проблемы
Дана плоскость .
Из точки А опущен перпендикуляр на плоскость .
В плоскости проведена прямая с .
Вопрос: 1.Как
найти расстояние
В находиться
до прямой с?основание отрезка,
Создается
проблемная
ситуация: от
Гдеточки
будет
2.Как найти
расстояние
определяющего
расстояние
от Аот
доточки
с? А до прямой с?
Как расположенны друг относительно друга прямая с и АМ?
А
П-Р
В
Н-я
П-я
М
с

9.

Обобщаем, делаем вывод, формулируем теорему.
А
А
В
В
с
с
А
В
М
с
М
Прямая, проведенная в
плоскости через основание
наклонной, перпендикулярно к
ее проекции на эту плоскость,
перпендикулярна и
к самой наклонной.

10.

Сформулируйте утверждения, обратные данным:
1) В равнобедренном
треугольнике углы при
основании равны.
2) Если две
параллельные прямые
пересечены секущей,
то накрест лежащие
углы равны.
3) В прямоугольном
треугольнике квадрат
гипотенузы равен сумме
квадратов катетов
Если в треугольнике углы
при основании равны, то
этот треугольник
равнобедренный
Если при пересечении двух
прямых секущей, накрест
лежащие углы равны, то эти
прямые параллельны.
Если квадрат одной
стороны треугольника
равен сумме квадратов
двух других его сторон,
то этот треугольник
прямоугольный.

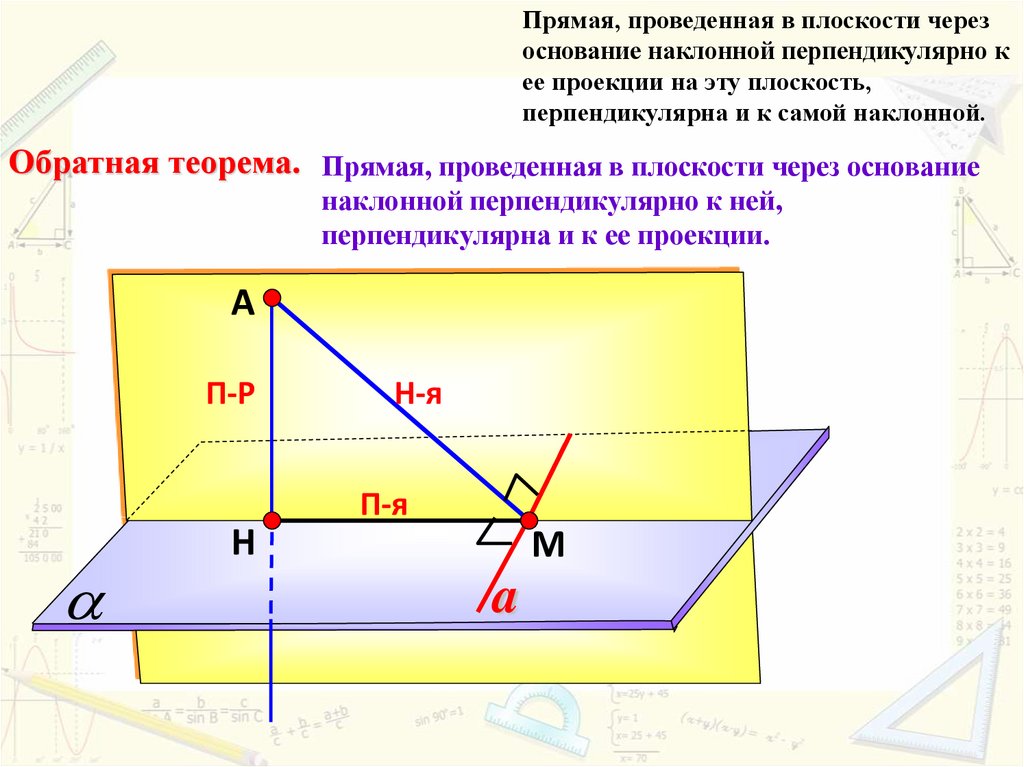
11.

Прямая, проведенная в плоскости через
основание наклонной перпендикулярно к
ее проекции на эту плоскость,
перпендикулярна и к самой наклонной.
Обратная теорема. Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
П-Р
Н-я
П-я
Н
М
a

12.

Математика
«Гений состоит из одного
процента вдохновения и 99
процентов потения»
Эдисон американский изобретатель.

13.

№148.
Прямая АК перпендикулярна к плоскости правильного
треугольника АВС, а точка М – середина стороны ВС. Докажите,
что МК ВС.
К
П-р
А
В
П-я
М
С
BC AМ
П-я
BC MК
TTП
Н-я

14.

№150.
Через вершину А прямоугольника АВСD проведена прямая АК,
перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см,
КВ = 7 см, КС = 9 см. Найдите:
а) расстояние от точки К до плоскости прямоугольника АВСD;
б) расстояние между прямыми АК и СD.
K
КА – искомое расстояние
АD – общий перпендикуляр
АD – искомое расстояние
6
D
9
П-я 1
С
П-Р
?
А
Найдем другие прямые углы…
TTП
СD AD
П-я 1
7
CD Н-яDK1
TTП
BC BA BC BK
П-я 2
Н-я 2
В

15.

« Если запастись терпением
и проявить старание, то
посеянные семена знания
непременно дадут добрые
всходы»,
Леонардо да Винчи.

16.

Домашнее задание.
П.19,20, № 147, №149,
Индивидуально: найти различные
способы доказательства теоремы о
трех перпендикулярах.

17.

Рефлексия
Я конечно не Ай-да я,
ленился, но и
ай-да
очень не
молодец!
трудился
Скажу
опять, что
я не понял

18.

№155.
Через вершину прямого угла С равнобедренного прямоугольного
треугольника АВС проведена прямая СМ, перпендикулярная к его
плоскости. Найдите расстояние от точки М до прямой АВ, если
АС = 4 см, а СМ = 2 7 см.
М
П-р
2 7
С
А
4
П-я
F
В
AВ СF
П-я
AВ MF
TTП
МF – искомое расстояние
Н-я

19.

№147.
Из точки М проведен перпендикуляр МВ к плоскости
прямоугольника АВСD. Докажите, что треугольники АМD и
МСD прямоугольные.
TTП
AD AM
П-я 1
AD AB
М
Н-я 1
DC BC
П-Р
А
П-я 1
D
П-я 2
В
С
DC CM
TTП
Н-я 2

20.

№149 (дом.)
Отрезок АD перпендикулярен к плоскости равнобедренного треугольника АВС.
Известно, что АВ = АС = 5 см, ВС = 6 см, АD = 12 см.
Найдите расстояния от концов отрезка АD до прямой ВС.
D
П-р
В
12
П-я
А
N 6
5
С
BC AN
П-я
BC DN
TTП
Н-я
АN и DN – искомые расстояния