Функция y = f(x)

1.

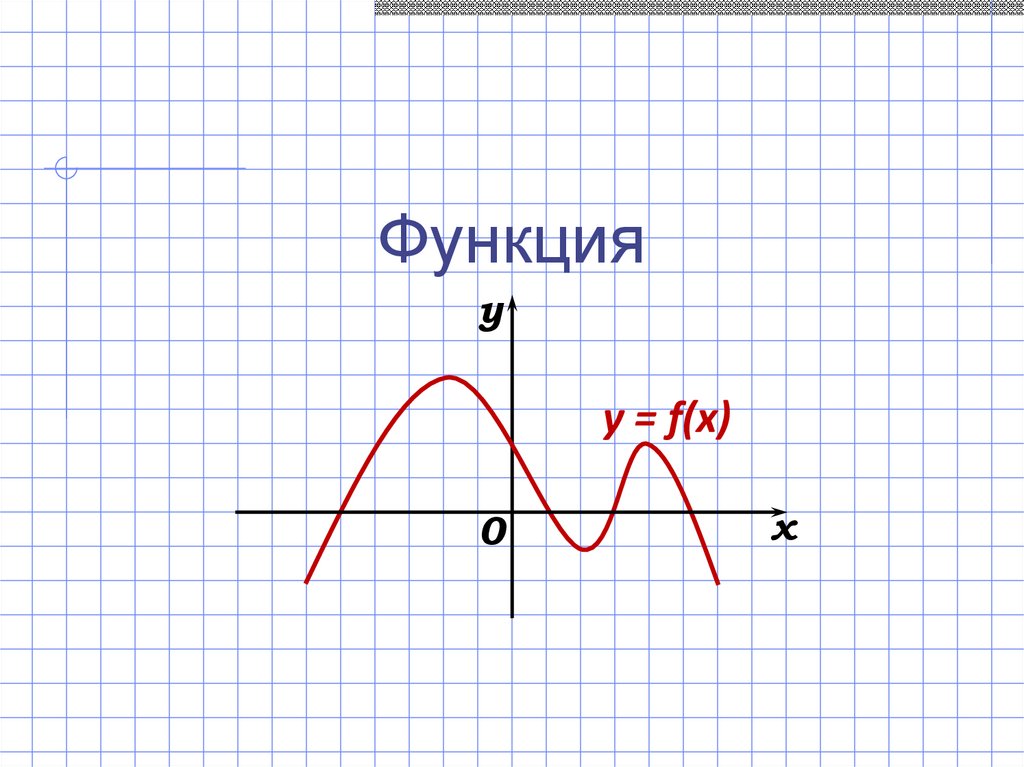
Функция
y
y = f(x)
0
x

2.

Понятие функции
Если каждому значению х из некоторого
множества чисел поставлено в соответствие
число у, то говорят, что на этом множестве
задана функция у(х).
При этом х называют независимой переменной
или аргументом,
а у – зависимой переменной или функцией.
y = f(x)

3.

Область определения и
множество значений функции
Областью определения функции называют
множество всех значений, которые может
принимать ее аргумент.
Обозначается D(y)
Множество значений (или область значений)
функции – это множество всех значений
переменной у.
Обозначается E(y)

4.

Примеры нахождения области определения
1)
y 3x 2 4 x 1
Решение:
Поскольку
3x 2 4 x 1
– многочлен, то область определения – все действительные значения х:
D( y) ;
2)
.
y
5
x 7
Решение:
Учитывая, что знаменатель не равен нулю, получаем:
x 7 0, x 7, D( y) ;7 7;
3) y 3 x 6
Решение:
Учитывая, что подкоренное выражение должно быть неотрицательным,
получаем:
3x 6 0, 3x 6, x 2, D( y) 2;

5.

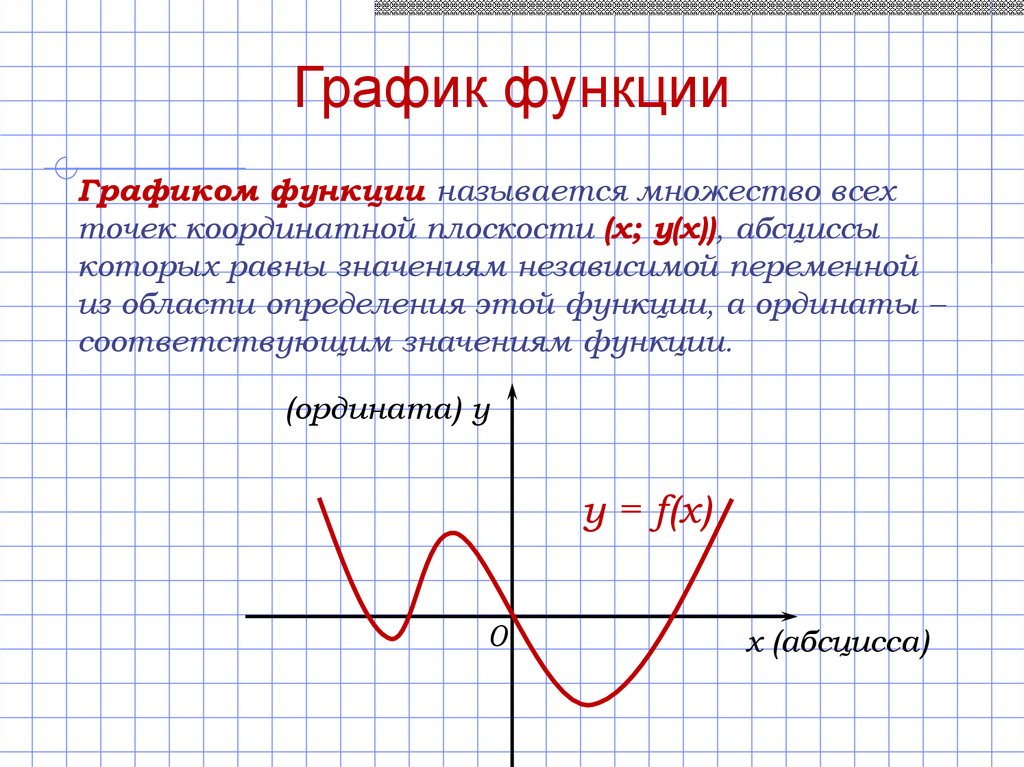
График функции
Графиком функции называется множество всех
точек координатной плоскости (х; у(х)), абсциссы
которых равны значениям независимой переменной
из области определения этой функции, а ординаты –
соответствующим значениям функции.
(ордината) y
y = f(x)
0
x (абсцисса)

6.

Способы задания функции:
• аналитический (с помощью формулы);
• графический (с помощью графика);
• табличный (с помощью таблицы значений);
• словесный (правило задания функции
описывается словами).

7.

Вспомним основные
элементарные
функции и их графики

8.

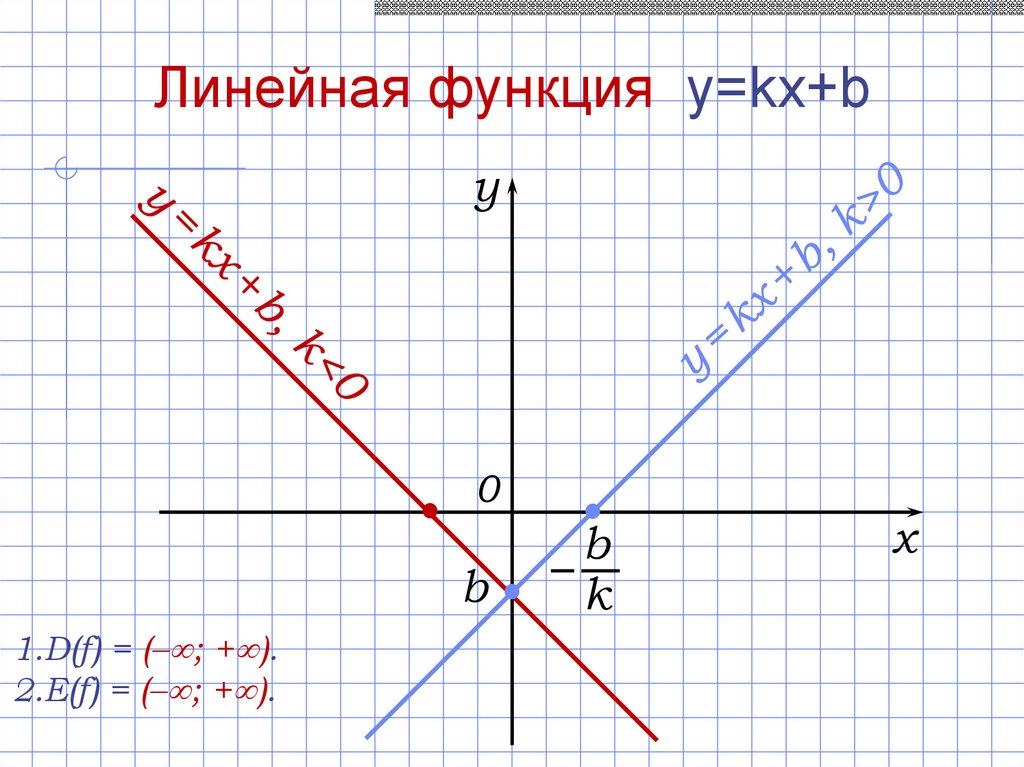
Линейная функция y=kx+b
y
0
b
1.D(f) = (– ; + ).
2.E(f) = (– ; + ).
b
k
x

9.

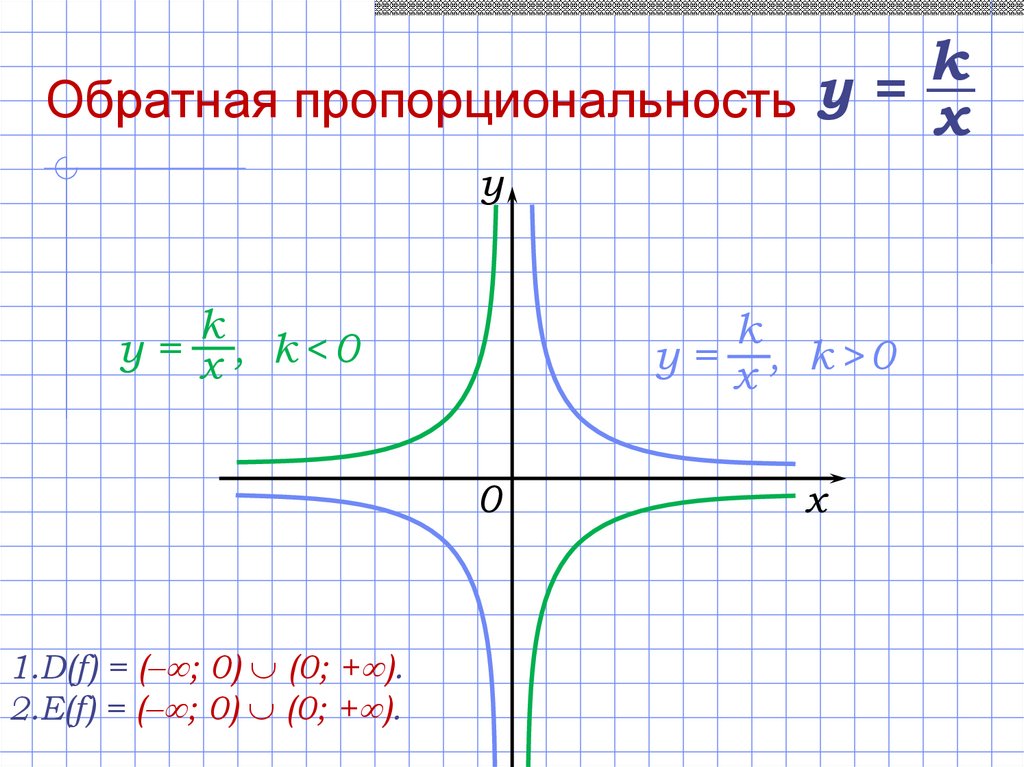
k
Обратная пропорциональность у = x
y
k
у = x , k<0
k
у = x , k>0
0
1.D(f) = (– ; 0) (0; + ).
2.E(f) = (– ; 0) (0; + ).
x

10.

Квадратичная функция y=kx2
Свойства функции y = kx2 при k > 0:
1.D(f) = (– ; + ).
2.E(f) = [0; + ).
Свойства функции y = kx2 при k < 0:
1.D(f) = (– ; + ).
2.E(f) = (– ; 0].

11.

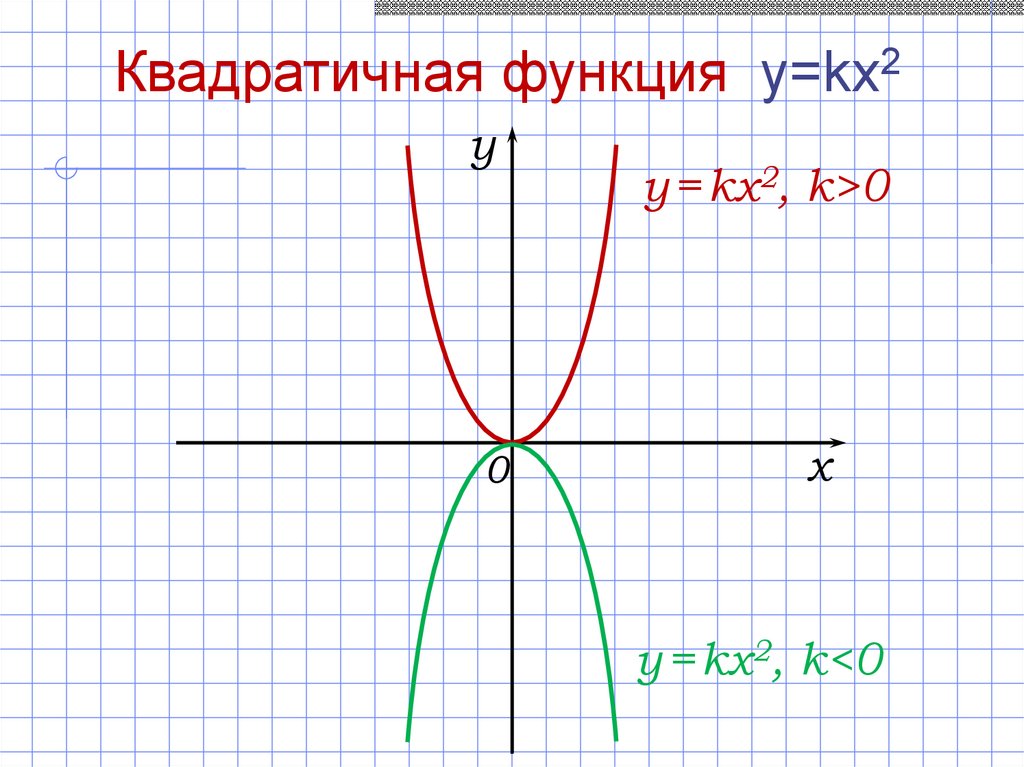
Квадратичная функция y=kx2
y
0
y = kx2, k>0
x
y = kx2, k<0

12.

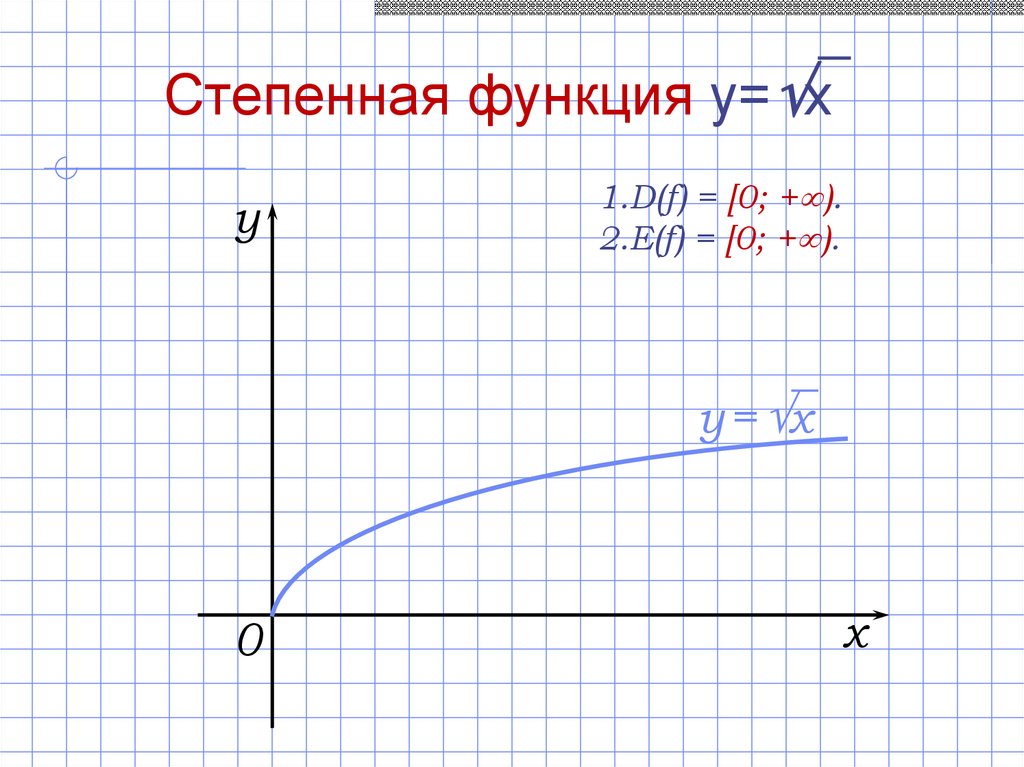
Степенная функция y= x
y
1.D(f) = [0; + ).
2.E(f) = [0; + ).
y = x
0
x

13.

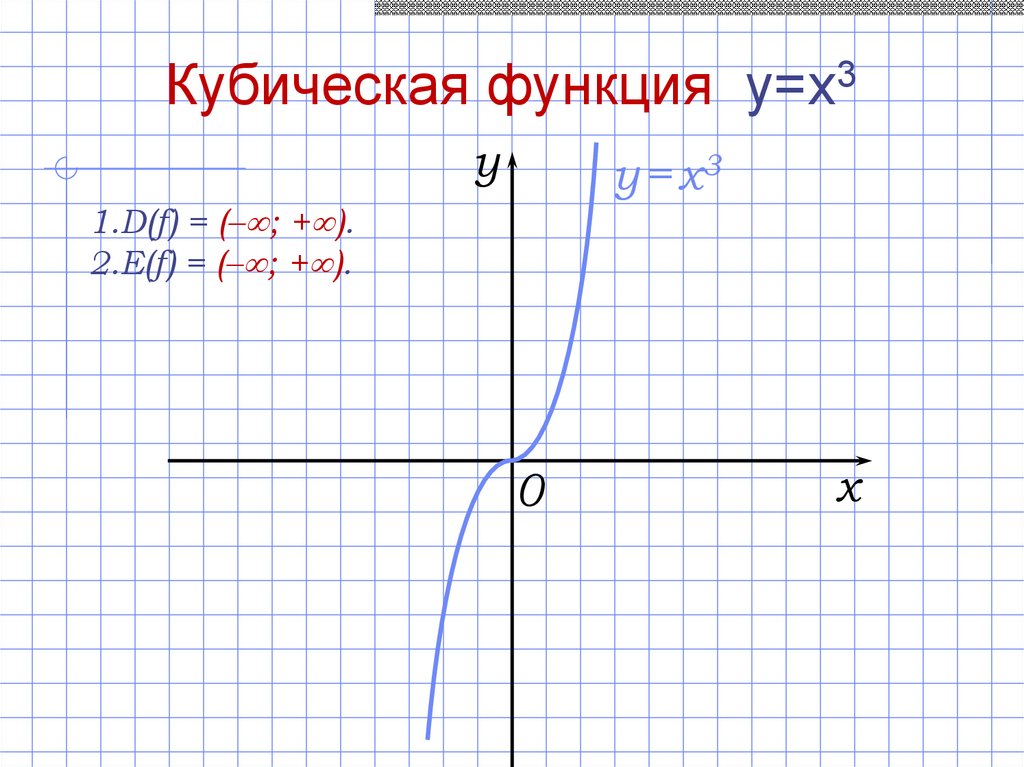
Кубическая функция y=x3
y
y = x3
1.D(f) = (– ; + ).
2.E(f) = (– ; + ).
0
x