Теорема Пифагора. О Пифагоре

1. Теорема Пифагора

2. Содержание

О Пифагоре.
Из истории теоремы.
Разминка.
Доказательство теоремы.
Закрепление материала.
Решение старинных задач.

3. Что известно о Пифагоре

В VI веке до н.э. в Древней Греции жил ученый Пифагор
родом из Самоса.
В молодости он много путешествовал по странам
Востока, побывал в Египте и Вавилоне, где изучал
разные науки, в том числе математику.
Вернувшись на родину, Пифагор основал философскую
школу закрытого типа- Пифагорейский союз. Каждый
вступающий в него отрекался от имущества и давал
клятву хранить в тайне учение основателя.
Пифагорейцы занимались математикой, философией,
естественными науками. Ими были сделаны важные
открытия в арифметике и геометрии.
В школе существовало правило, по которому авторство
работ присваивалось Пифагору. Так что неизвестно,
какие открытия принадлежат самому учёному.

4. Из истории теоремы

S
S1
S2
«Площадь квадрата,
построенного на гипотенузе
прямоугольного треугольника,
равна сумме площадей
квадратов, построенных на его
катетах», или в виде задачи:
«Доказать, что квадрат,
построенный на гипотенузе
прямоугольного треугольника,
равновелик сумме квадратов,
построенных на катетах:
S=S1+S2» - так
формулировали теорему во
времена Пифагора

5. Из истории теоремы

Долгое время считалось, что до Пифагора эта
теорема не была известна.
В настоящее время установлено, что она
встречается в вавилонских текстах, написанных
за 1200 лет до Пифагора! Вероятно тогда
теорема ещё не была доказана, а соотношение
между катетами и гипотенузой было получено
опытным путём.
Была она известна и древним китайцам, и
индусам.
Таким образом, Пифагор не открыл замечательное
свойство прямоугольного треугольника, но,
вероятно, первым обобщил и доказал его,
перенеся таким самым из области практики в
область науки. К сожалению, сведения о
доказательстве до нес не дошли.

6. Из истории теоремы

а
c
b
Сегодня известно более ста
различных доказательств
теоремы Пифагора
Вероятно соотношение между
катетами и гипотенузой
первоначально было
установлено для
равнобедренного
прямоугольного треугольника.
По рисунку видим, что квадрат, построенный на
его гипотенузе, разбивается диагоналями на
четыре равных треугольника, а квадраты,
построенные на катетах, содержат по два таких
же треугольника. Замечаем, что площадь
большого квадрата равна сумме площадей малых
квадратов

7. Из истории теоремы

Учащиеся средних веков считали
доказательство теоремы очень
трудным и прозвали его «ослиным
мостом» или «бегством убогих»,
так как слабые ученики бежали от
геометрии, а те, кто заучивал
теоремы наизусть, без понимания,
были не в состоянии осилить
теорему Пифагора: она служила
для них чем-то вроде
непреодолимого моста.
Из-за иллюстрирующих теорему чертежей учащиеся
называли её также «ветряной мельницей», рисовали
забавные карикатуры и придумывали стишки:
«Пифагоровы штаны
Во все стороны равны»

8. Из истории теоремы

с
а
b
Теорема Пифагора
занимает в геометрии
особое место.
На её основе можно
вывести или доказать
большинство теорем.
А ещё она замечательна
тем, что сама по себе вовсе
не очевидна.
Сколько не рассматривай
прямоугольный
треугольник, никак не
увидишь, что его стороны
а, b, с связывает простое
соотношение
а²+ b²= с²

9. Разминка

1. Определите вид
треугольника,
изображенного на
рисунке.
2. Как называются
стороны такого
треугольника?
3.Укажите названия
каждой стороны
данного
треугольника.

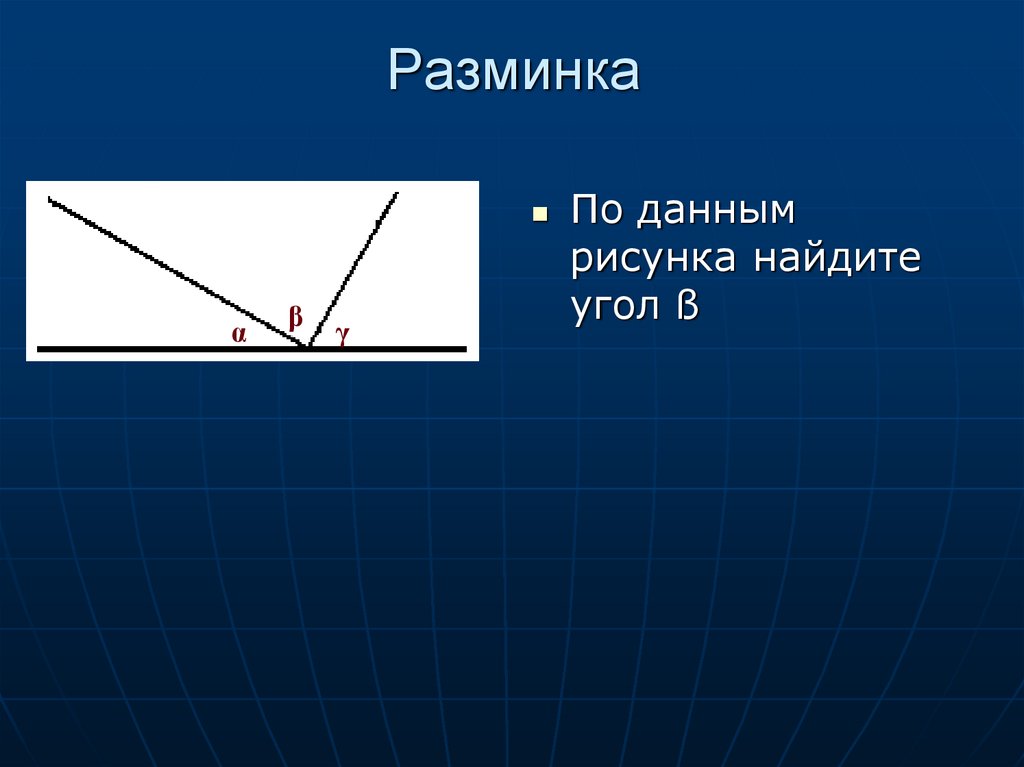
10. Разминка

α
β
γ
По данным
рисунка найдите
угол ß

11. Разминка

В
M
С
N
K
А
P
D
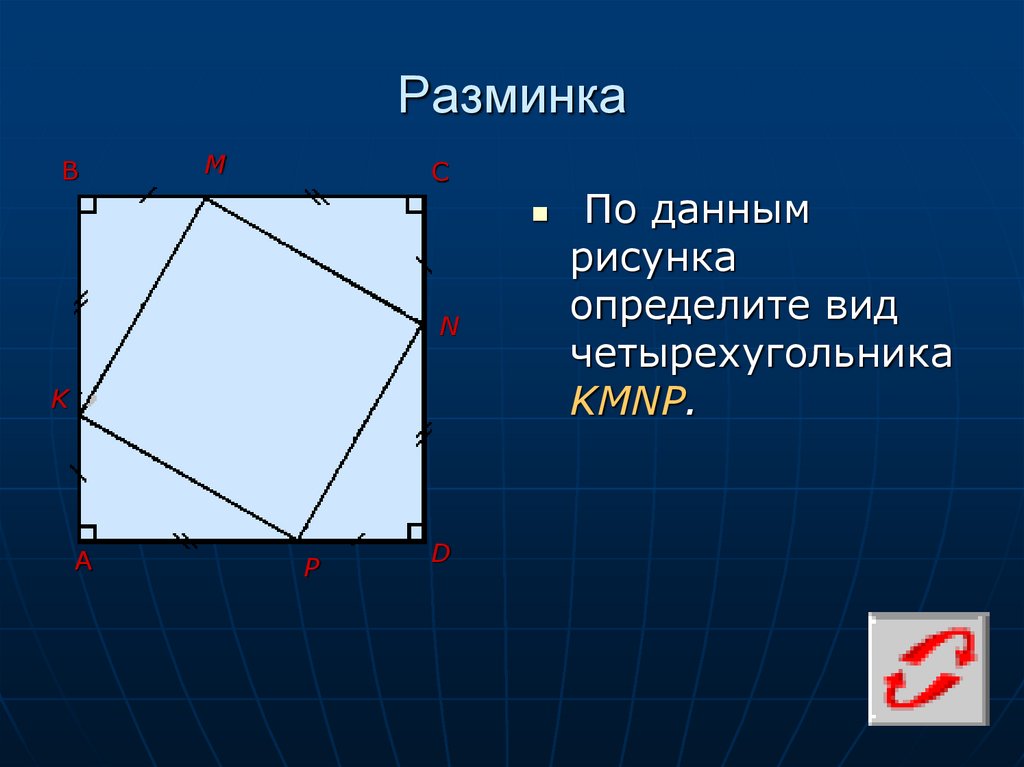
По данным
рисунка
определите вид
четырехугольника
KMNP.

12. Доказательство теоремы

b
c
а
Доказательство:
рассмотрим
прямоугольный
треугольник с катетами
а,b и гипотенузой с.
Докажем, что
с2=a2+b2
Достроим треугольник
до квадрата со стороной
а+b

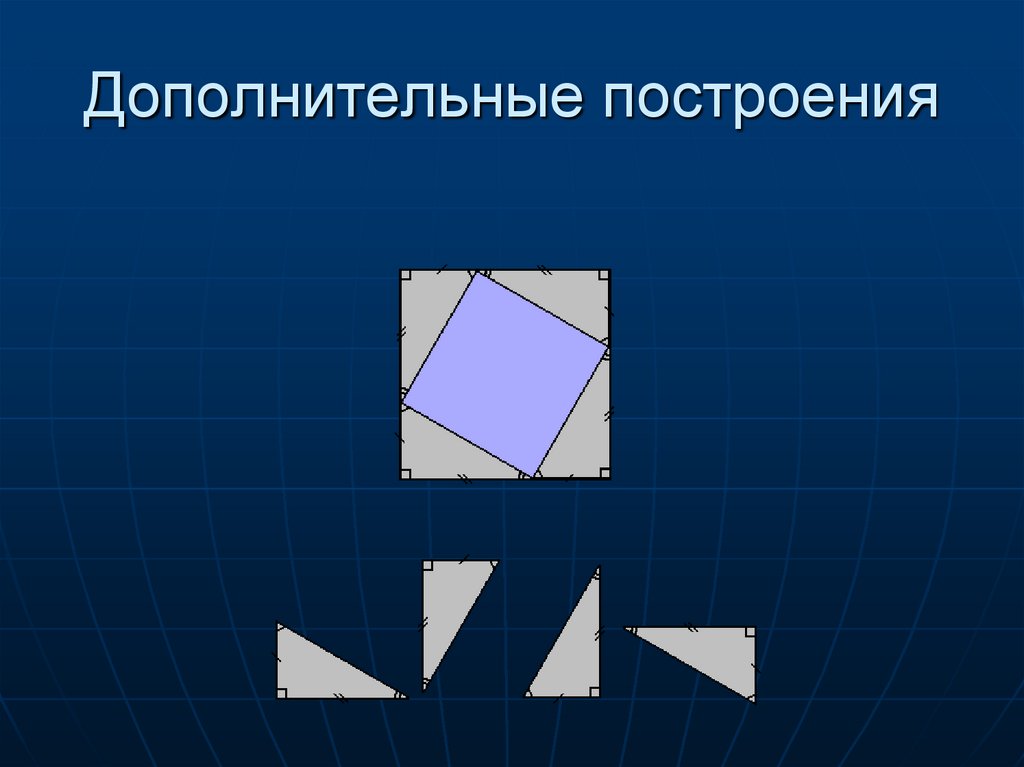
13. Дополнительные построения

14. Доказательство теоремы

а
b
а
b
с
с
b
Площадь S этого квадрата равна
(а+b)2. С другой стороны, этот
квадрат составлен из четырёх
равных прямоугольных
треугольников, площадь каждого
из которых равна ½а·b и
квадрата со стороной с (его
площадь равна с2),
поэтому
S=4 ·½аb+с2=2аb+с2,
Таким образом,
(а+b)2=2аb+с2 ,
Откуда
а
с
с
а
b
с2=a2+b2
Теорема доказана.

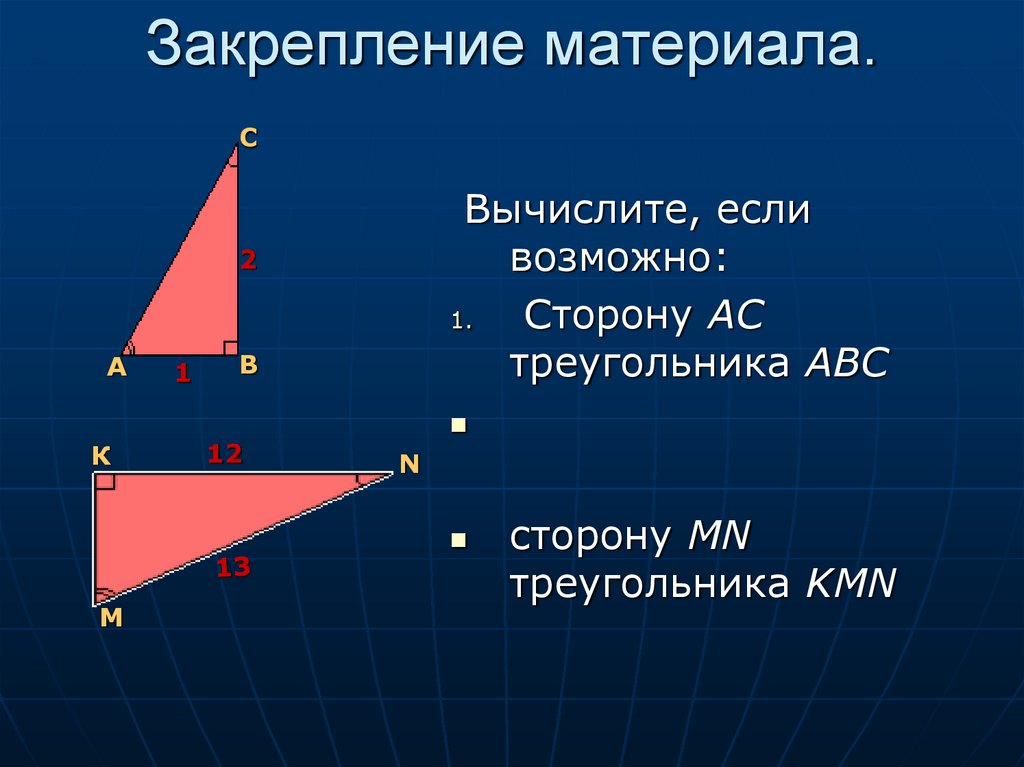
15. Закрепление материала.

С
Вычислите, если
возможно:
1.
Сторону АС
треугольника АВС
2
А
К
1
В
12
N
М
сторону MN
треугольника KMN

16. Закрепление материала

С
D
1
F
В
Р
К
5
3
R
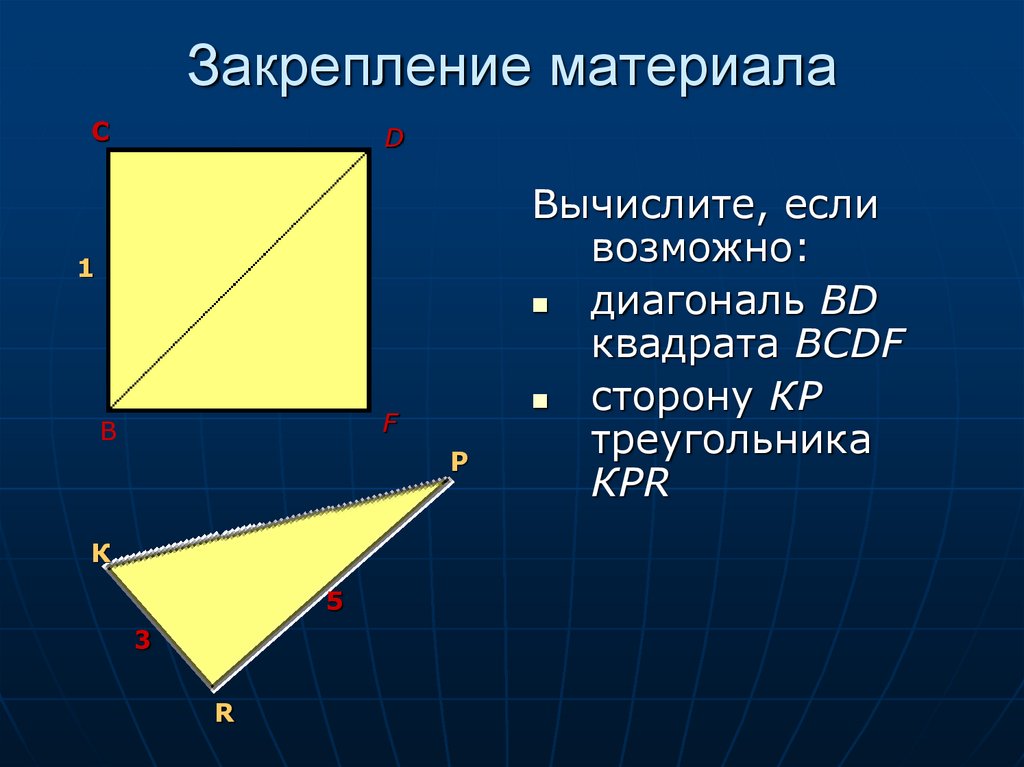
Вычислите, если
возможно:
диагональ ВD
квадрата BCDF
сторону КР
треугольника
КРR

17. Закрепление материала

В
С
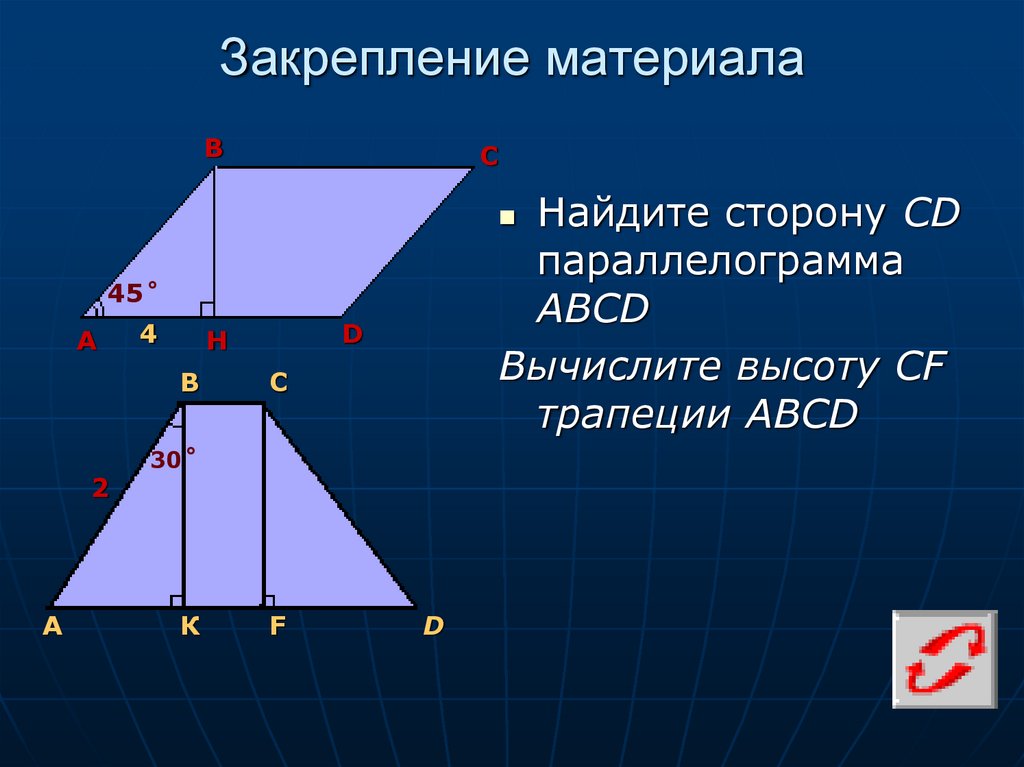
Найдите сторону CD
параллелограмма
АВСD
Вычислите высоту CF
трапеции ABCD
45˚
А
4
В
2
А
D
Н
С
30˚
К
F
D

18. Решение

А
117
125
С
В
Р е ш е н и e. Треугольник
АВС - прямоугольный
Пусть ВС = х стоп,
тогда по теореме Пифaгopa
АС2 + СВ2 =АВ2,
1172 +x2= 1252;
х2 = 1252 - 1172,
х2 = (125- 117)(125 + 117),
х2=8·242, х=44.
О т в е т: 44 стопы

19. Задача Бхаскары (индийского математика XII в.)

На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал...
Бедный тополь упал. И угол прямой
C теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота

20. Решение

Пусть, АВ- высота
тополя, тогда
АВ=АС+СD.
Найдём СD.
Треугольник АСDпрямоугольный.
По теореме Пифагора
СD²=АС²+АD²,
СD²=3² +4²,
откуда
СD= 5 футов.
Значит,
АВ=3+5=8 футов

21. Из древнеиндийского трактата

Над озером тихим,
C полфута размером, высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону.
Нет боле цветка над водой.
Нашёл же рыбак его ранней весной
B двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
½
С
А
2
В

22. Решение

½
С
2
В
А
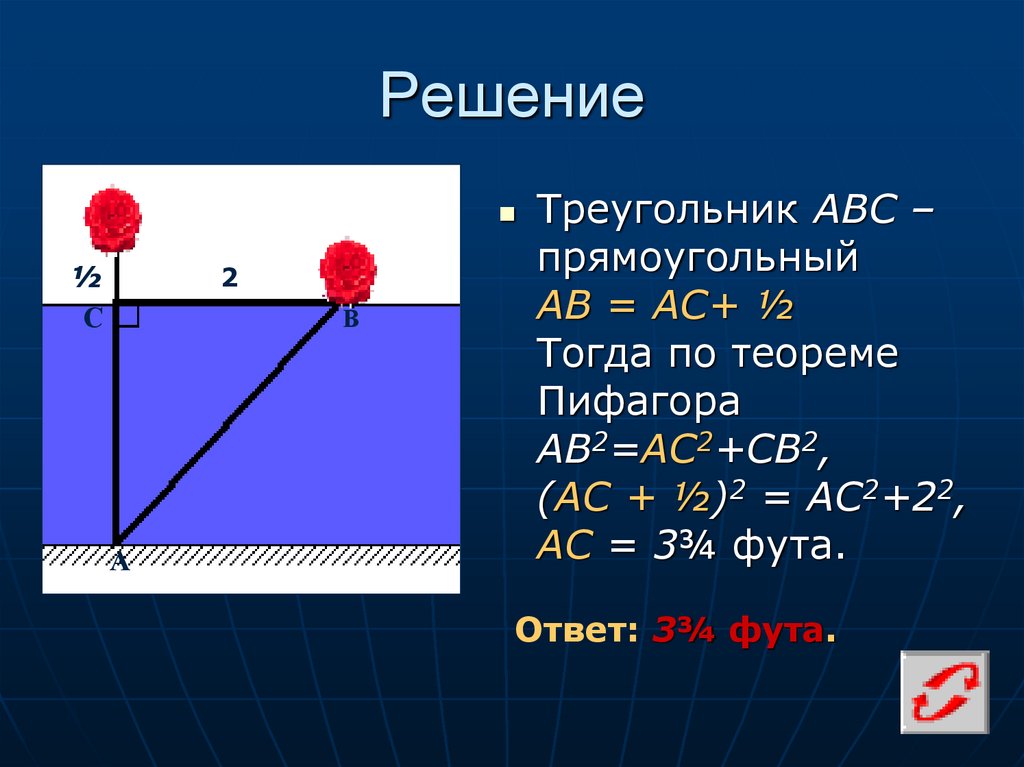
Треугольник АВС –
прямоугольный
АВ = АС+ ½
Тогда по теореме
Пифагора
AB2=AC2+CB2,
(АС + ½)2 = АС2+22,
АС = 3¾ фута.
Ответ: 3¾ фута.