Метод областей для решения систем неравенств с двумя переменными

1.

МЕТОД областей
для решения
СИСТЕМ НЕРАВЕНСТВ
С ДВУМЯ ПЕРЕМЕННЫМИ

2.

Иллюстрации к примерам объяснительного текста ПУНКТ 25
См. приложение в формате ЖГ

3.

Иллюстрации к примерам объяснительного текста ПУНКТ 25
См. приложение в формате ЖГ

4.

Иллюстрации к примерам объяснительного текста ПУНКТ 25
См. приложение в формате ЖГ

5.

ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ
(«переход» метода интервалов с прямой на плоскость)
Неравенства с
одной переменной
Метод интервалов:
1.ОДЗ
2. Корни
3. Ось
4. Знаки на
интервалах
5. Ответ.
Неравенства с
двумя переменной
Метод областей:
1. ОДЗ
2. Граничные линии
3. Координатная
плоскость
4. Знаки в областях
5.Ответ по рисунку.

6.

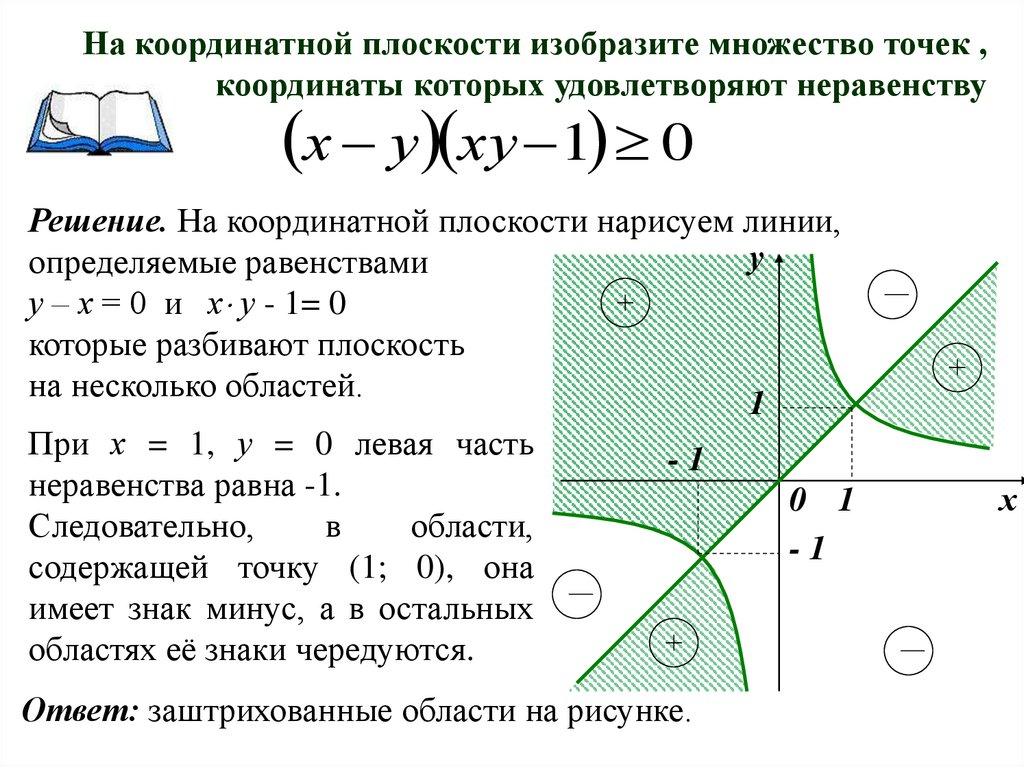
На координатной плоскости изобразите множество точек ,
координаты которых удовлетворяют неравенству
х у ху 1 0
Решение. На координатной плоскости нарисуем линии,
у
определяемые равенствами
у – х = 0 и х у - 1= 0
которые разбивают плоскость
на несколько областей.
1
При х = 1, у = 0 левая часть
-1
неравенства равна -1.
0 1
Следовательно,
в
области,
-1
содержащей точку (1; 0), она
имеет знак минус, а в остальных
областях её знаки чередуются.
Ответ: заштрихованные области на рисунке.
х

7.

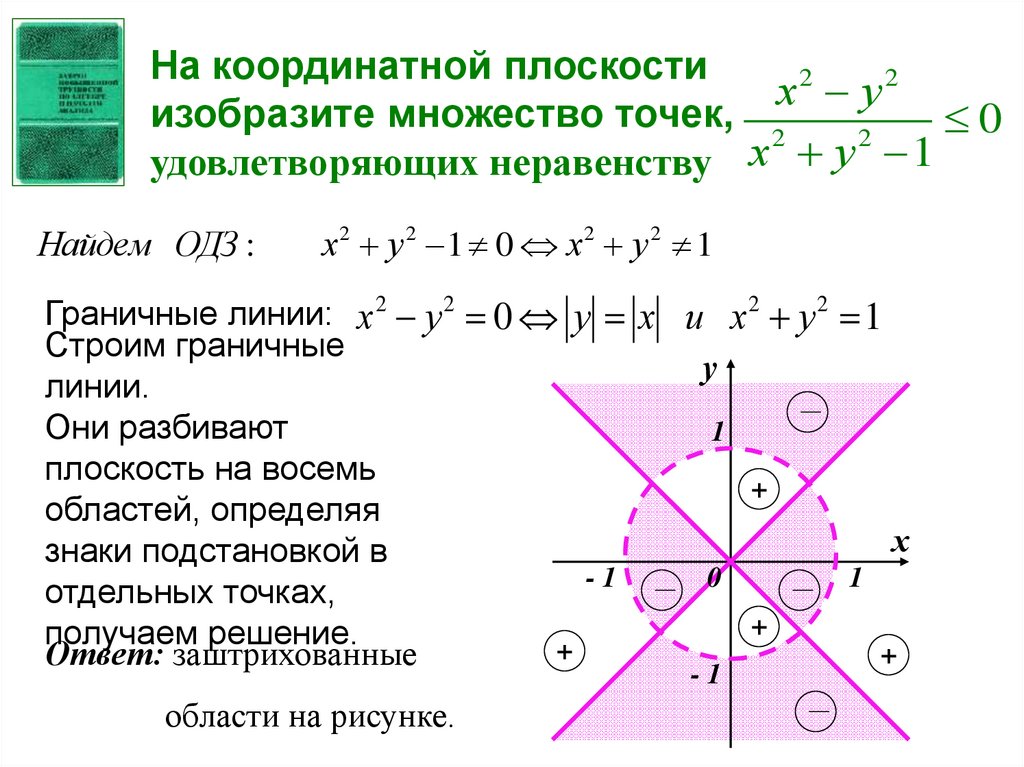
На координатной плоскости
х2 у 2
изобразите множество точек, 2
0
2
удовлетворяющих неравенству х у 1
Найдем ОДЗ :
х2 у 2 1 0 х2 у 2 1
Граничные линии: х 2 у 2 0 у х и х 2 у 2 1
Строим граничные
у
линии.
Они разбивают
1
плоскость на восемь
+
областей, определяя
х
знаки подстановкой в
-1
0
1
отдельных точках,
+
получаем решение.
+
+
Ответ: заштрихованные
-1
области на рисунке.

8.

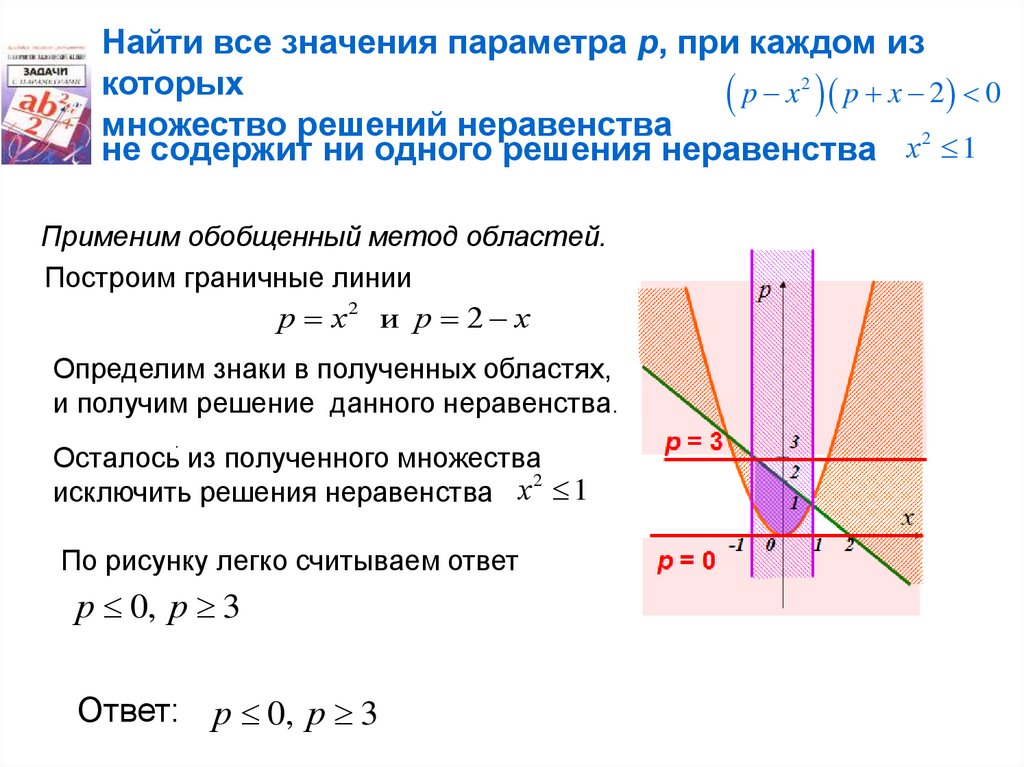
Найти все значения параметра р, при каждом из
которых
p x2 p x 2 0
множество решений неравенства
не содержит ни одного решения неравенства х 2 1
Применим обобщенный метод областей.
Построим граничные линии
р х2 и р 2 х
Определим знаки в полученных областях,
и получим решение данного неравенства.
.
Осталось из полученного множества
2
исключить решения неравенства х 1
По рисунку легко считываем ответ
р 0, р 3
Ответ: р 0, р 3

9.

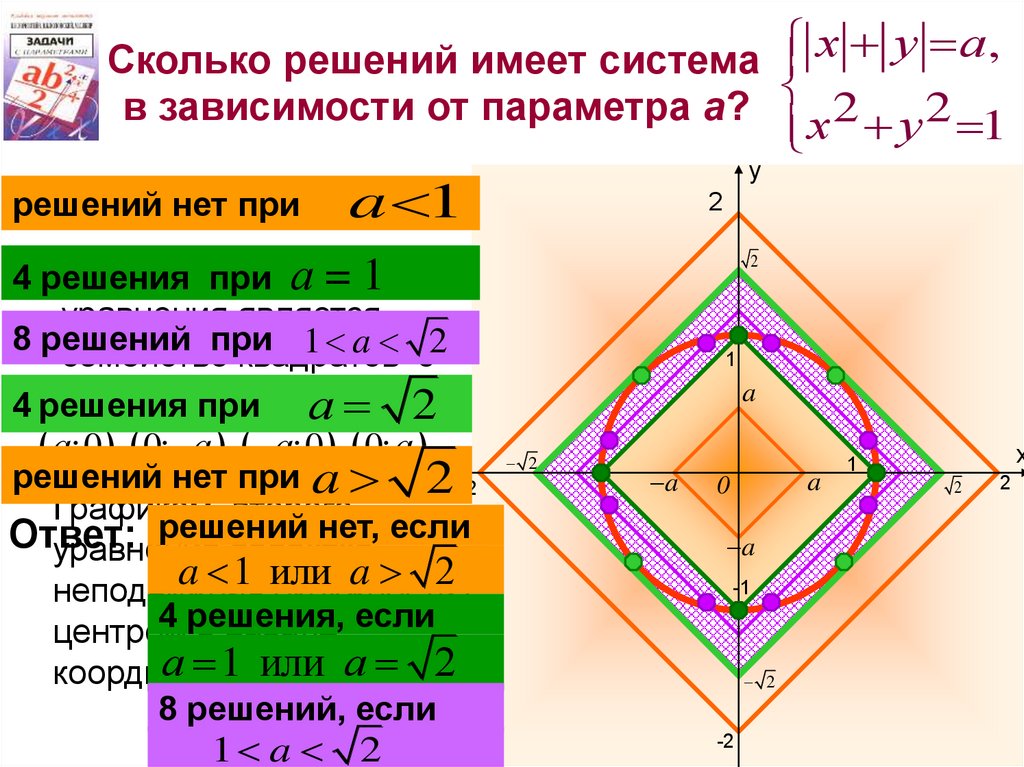
х у а,
Сколько решений имеет система
в зависимости от параметра а?
2 у 2 1
х
решений нет при
y
a 1
Графикомпри
первого
4 решения
а=1
уравнения является
8 решений
при
1 a с2
семейство
квадратов
вершинами
4 решения
прив точках
а 2
а;0 , 0; а , а;0 , 0; а
решений нет при a 2 -2
Графиком второго
решений нет, если
Ответ:
уравнения является
a 1 или a 2
неподвижная окружность с
4 решения,
центром
в начале если
а 1и радиусом
или а 12
координат
8 решений, если
1 a 2
2
2
1
a
2
a
a
0
a
-1
2
-2
x
1
2
2

10.

При каких положительных значениях 4 х 2 у 0
параметра а, система уравнений
2
2
2
х
у
а
4 х 1
имеет ровно четыре решения?
4
Запишем
систему в виде:
х 2 у
у
2
2
2
(
х
2)
у
а
.
а
2
2
решений нет при
Построим графики обоих уравнений.
Шаги построения первого уравнения:
4 решения при
2
а 2 2
Строим уголок у 4 х 2 , затем
у 4 х 2
и
симметрично
отображаем
относительно
8 решений при
2 2 a 4. оси
абсцисс.
-2
0
2
х
Второе уравнение задает семейство
окружностей
с центром (2;0) и
4 решения при
а 4
радиусом а.
Итак:
при а 2 2 решений нет; при а 2 2 и а 4 система имеет 4 решения;
система имеет 8 решений при 2 2 a 4.
Ответ: а 2 2 и а 4

11.

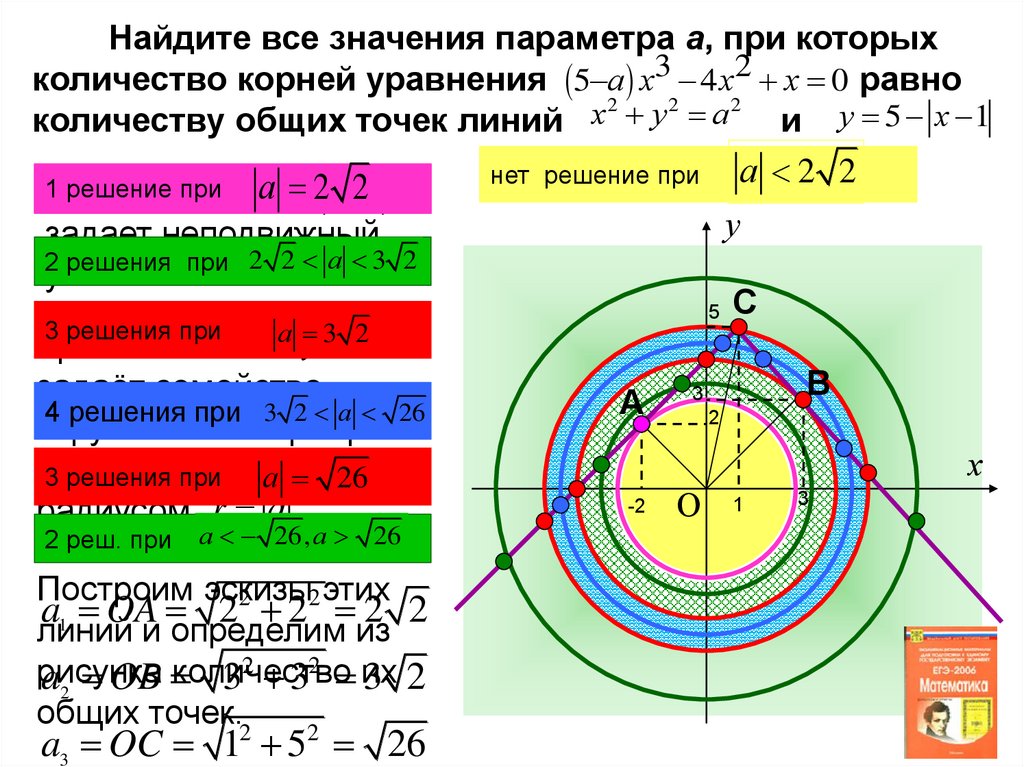
Найдите все значения параметра а, при которых
количество корней уравнения 5 а х3 4 х2 х 0 равно
2
2
2
х
у
а
количеству общих точек линий
и у 5 х 1
а 2 2
нет решение при
1
решение при у
а 5 2х 21
Уравнение
у
задает неподвижный
2 решения при 2 2 а 3 2
уголок.
5 С
3 решения при 2 а 23 2 2
у а
Уравнение х
В
задаёт семейство
3
А
4 решения при 3 2 а 26
2
окружностей с центром
х
в3 начале
координат
решения при
а 26и
3
-2
О 1
радиусом r а .
2 реш. при
а 26, a 26
Построим эскизы
2
2 этих
a1 OA 2 2 2 2
линий
и определим из
рисунка
количество
a2 OB
32 32 их
3 2
общих точек.2
2
a3 OC 1 5 26

12.

1 решение при
а 2 2
4 решения при 3 2 а 26
Запишем первое уравнение в виде х нет
5 а х 2 4 х 1 а
02 2
решение при
2 решения при 2 2 а 3 2
Заметим, что х = 0 – корень не зависимо от параметра а.
3 решения
2 реш. при а5 а 26,
3 2
х2a 4х26 1 0 может иметь
Уравнение
0, 1при
или 2арешения
в зависимости от параметра а и дискриминанта
a. 1
3 решения при D
а 4 26
одно решение Два решения
первое
уравнение
совокупность
линий
a 1
а = 5; а = 1
Три решения
a 1
а 2 2
3 2 a 2 2, а 3 2, а 26
а 2 2
2 2 a 3 2,
а 3 2,
а 26, a 26
а 26
Осталось заметить, что условие задачи выполняется только
в трех точках при а 2 2, а 3 2 и a 26
Ответ: а 2 2, а 3 2 и a 26

13.

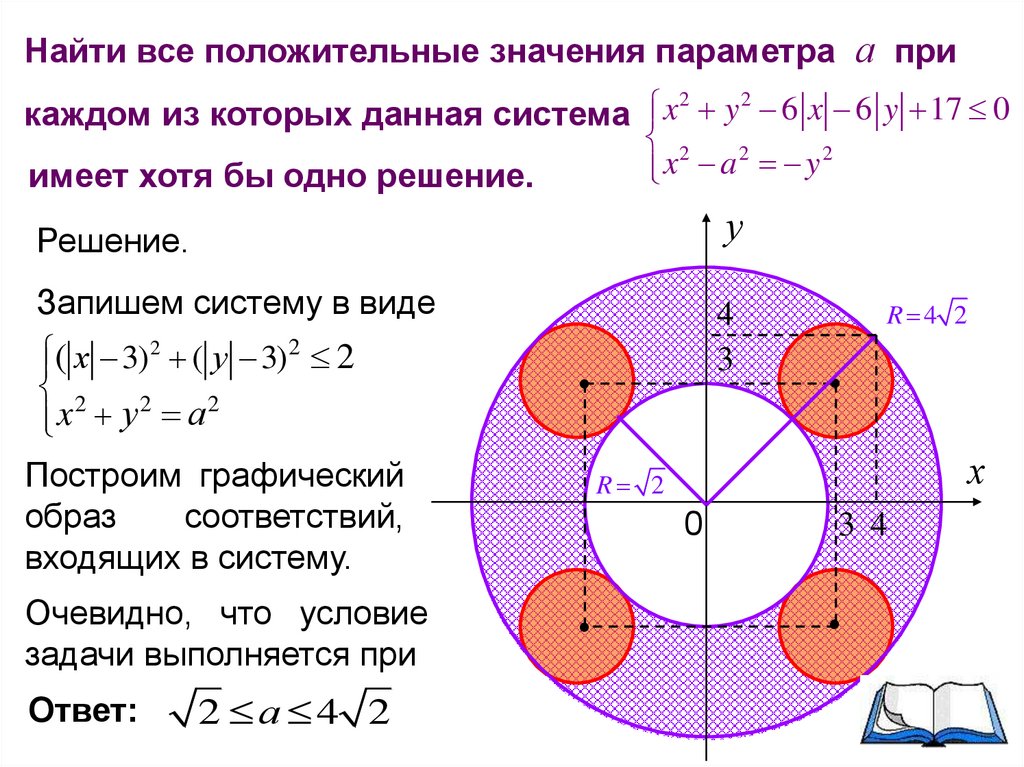
Найти все положительные значения параметра а при
2
2
x
y
6 x 6 y 17 0
каждом из которых данная система
2
2
2
x
a
y
имеет хотя бы одно решение.
у
Решение.
Запишем систему в виде
2
2
(
х
3)
(
у
3)
2
2
2
2
x
у
а
Построим графический
образ
соответствий,
входящих в систему.
Очевидно, что условие
задачи выполняется при
Ответ:
2 а 4 2
4
3
R 4 2
х
R 2
0
3 4