Similar presentations:
Расчёт надёжности систем со сложной структурой
1.
Задача №5Расчёт надёжности систем со
сложной структурой
2.
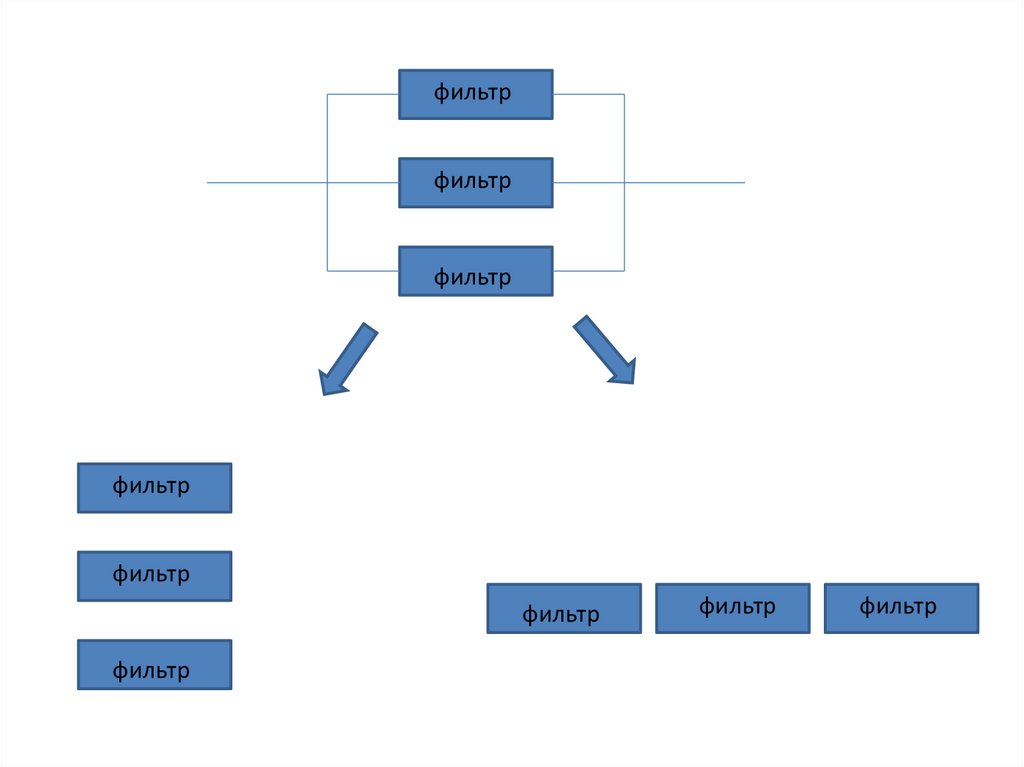
фильтрфильтр
фильтр
фильтр
фильтр
фильтр
фильтр
фильтр
фильтр
3.
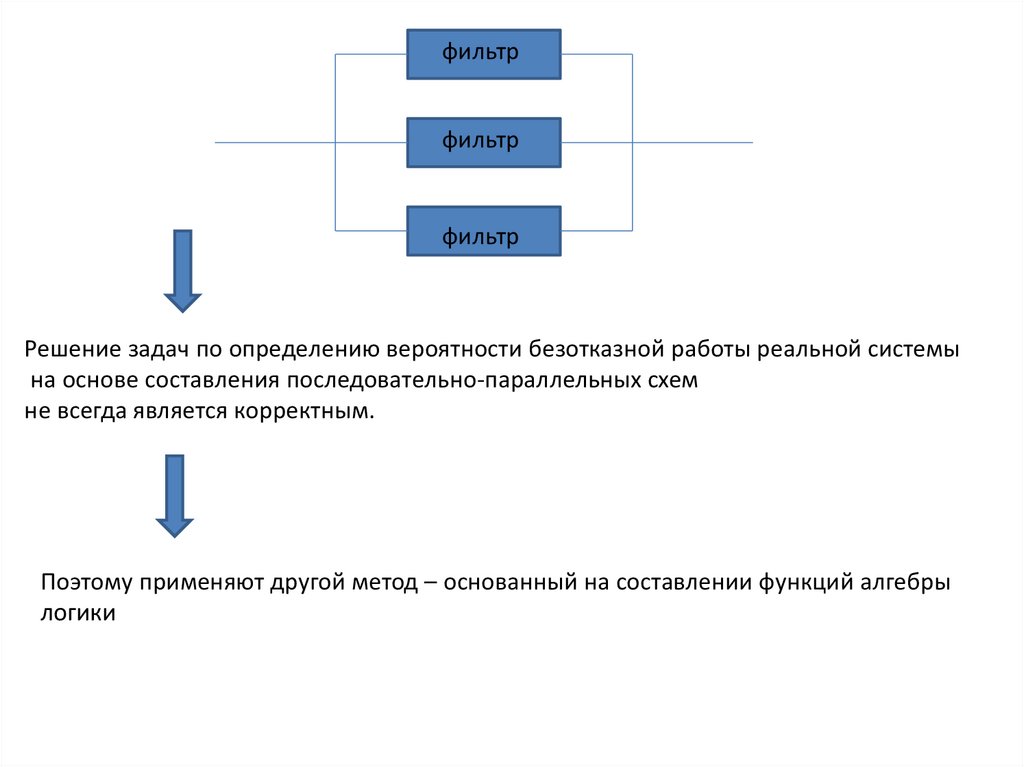
фильтрфильтр
фильтр
Решение задач по определению вероятности безотказной работы реальной системы
на основе составления последовательно-параллельных схем
не всегда является корректным.
Поэтому применяют другой метод – основанный на составлении функций алгебры
логики
4.
Рассмотрим на примере одного фильтра два несовместных событияфильтр
Событие «А» - фильтр полностью исправен
Событие «А» - фильтр неисправен (т.е. противоположное событие)
«Не» т.е. логическое отрицание
P(A)+P(A)=1
5.
P(A)+P(A)=1P(A)+q(A)=1
P(А)- вероятность безотказной работы
q(A)- вероятность отказа
P=1-q
6.
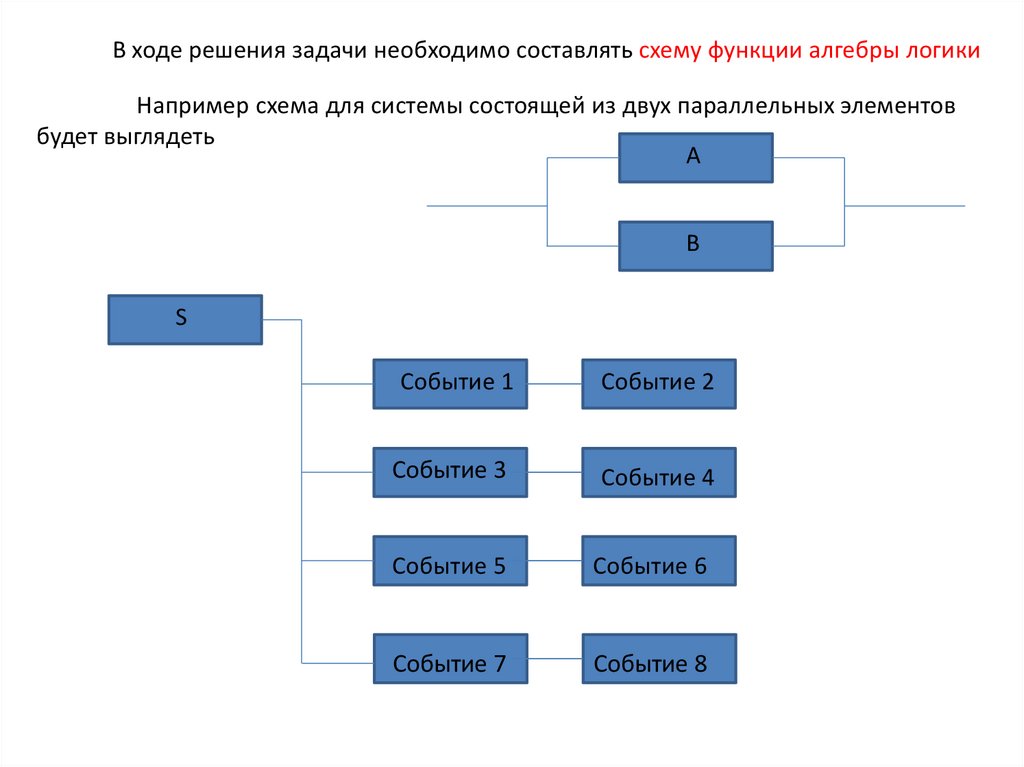
В ходе решения задачи необходимо составлять схему функции алгебры логикиНапример схема для системы состоящей из двух параллельных элементов
будет выглядеть
А
B
S
Событие 1
Событие 3
Событие 2
Событие 4
Событие 5
Событие 6
Событие 7
Событие 8
7.
SA
B
C
D
E
F
G
H
Два вида связей: горизонтальные и вертикальные
При составлении уравнения: горизонтальные связи умножаются
вертикальные складываются
S=AB+CD+EF+GH
8.
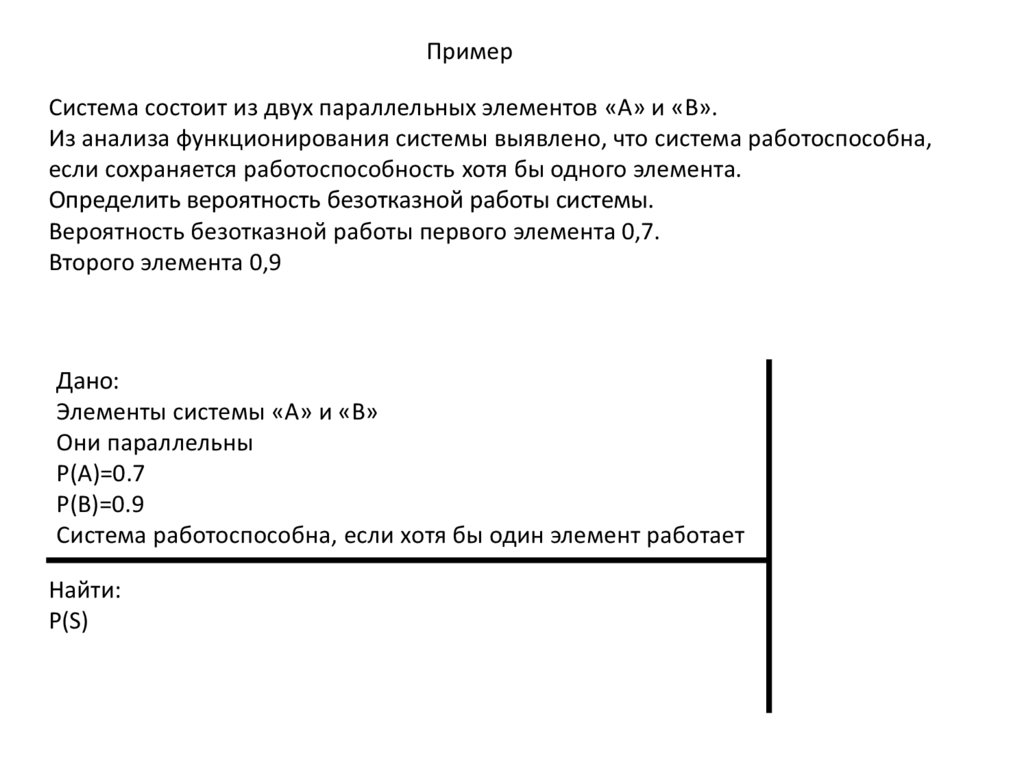
ПримерСистема состоит из двух параллельных элементов «A» и «B».
Из анализа функционирования системы выявлено, что система работоспособна,
если сохраняется работоспособность хотя бы одного элемента.
Определить вероятность безотказной работы системы.
Вероятность безотказной работы первого элемента 0,7.
Второго элемента 0,9
Дано:
Элементы системы «A» и «B»
Они параллельны
P(A)=0.7
P(B)=0.9
Система работоспособна, если хотя бы один элемент работает
Найти:
P(S)
9.
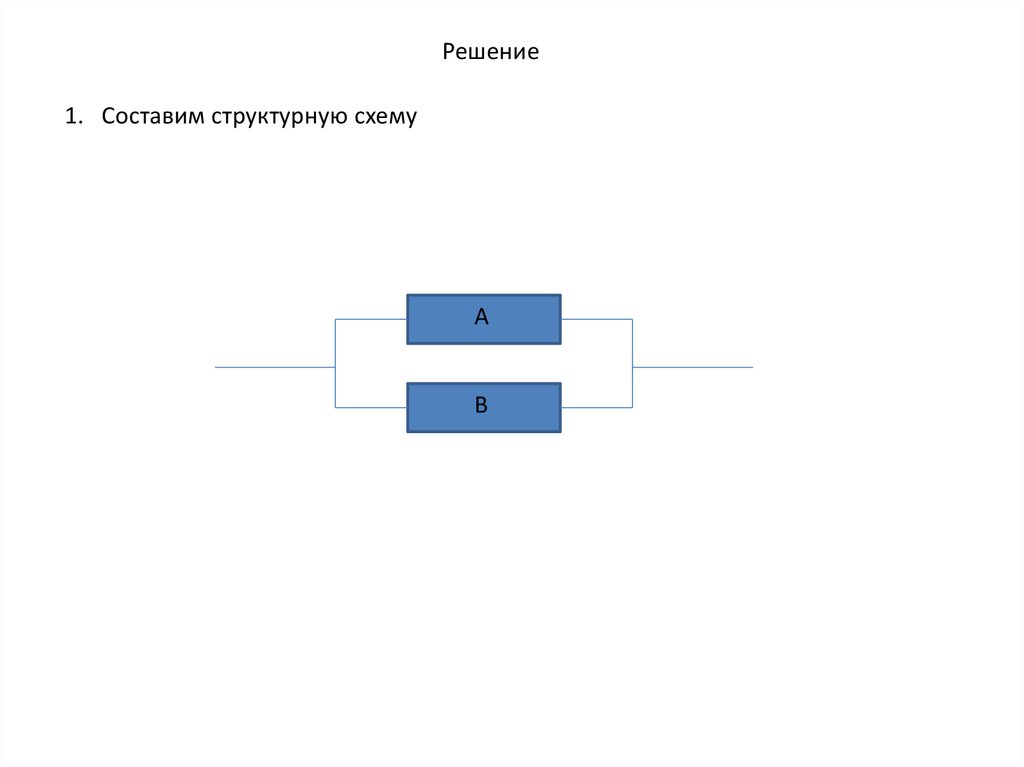
Решение1. Составим структурную схему
А
B
10.
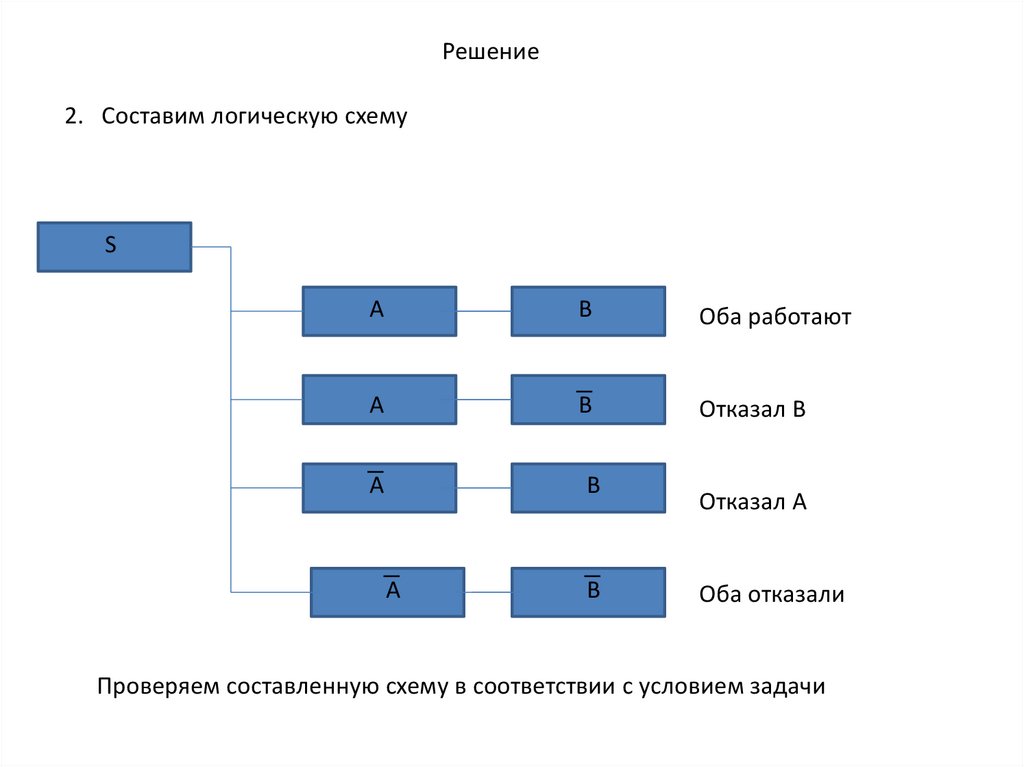
Решение2. Составим логическую схему
S
A
B
Оба работают
A
B
Отказал B
A
B
A
B
Отказал А
Оба отказали
Проверяем составленную схему в соответствии с условием задачи
11.
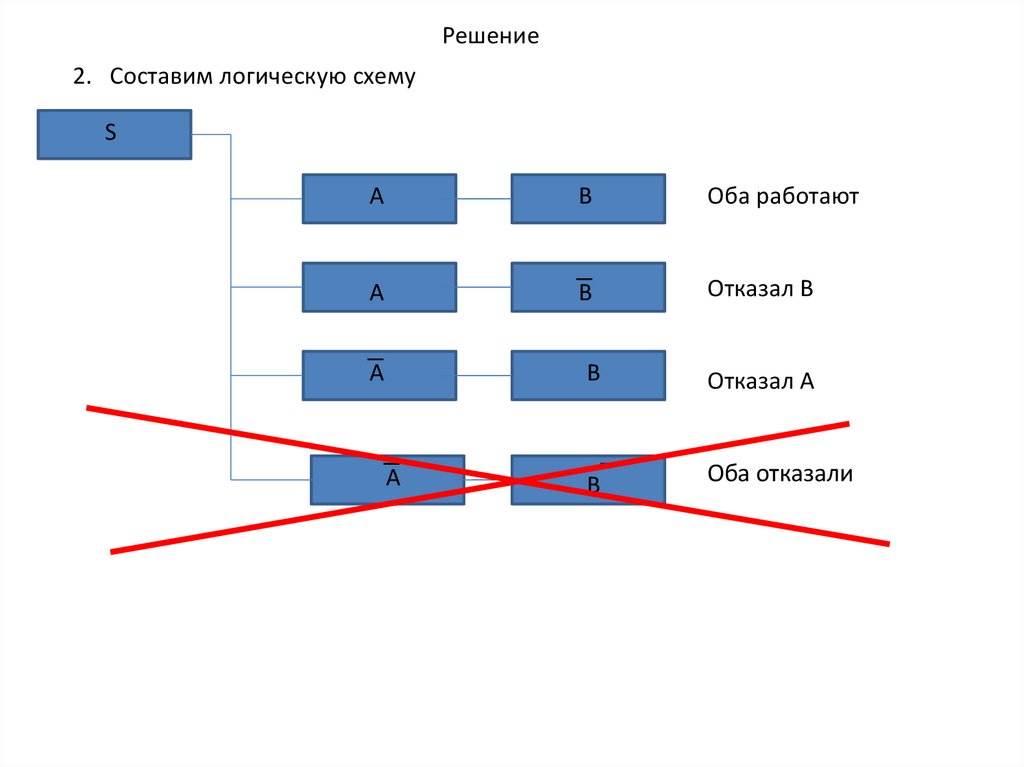
Решение2. Составим логическую схему
S
A
B
Оба работают
A
B
Отказал B
A
A
B
Отказал А
B
Оба отказали
12.
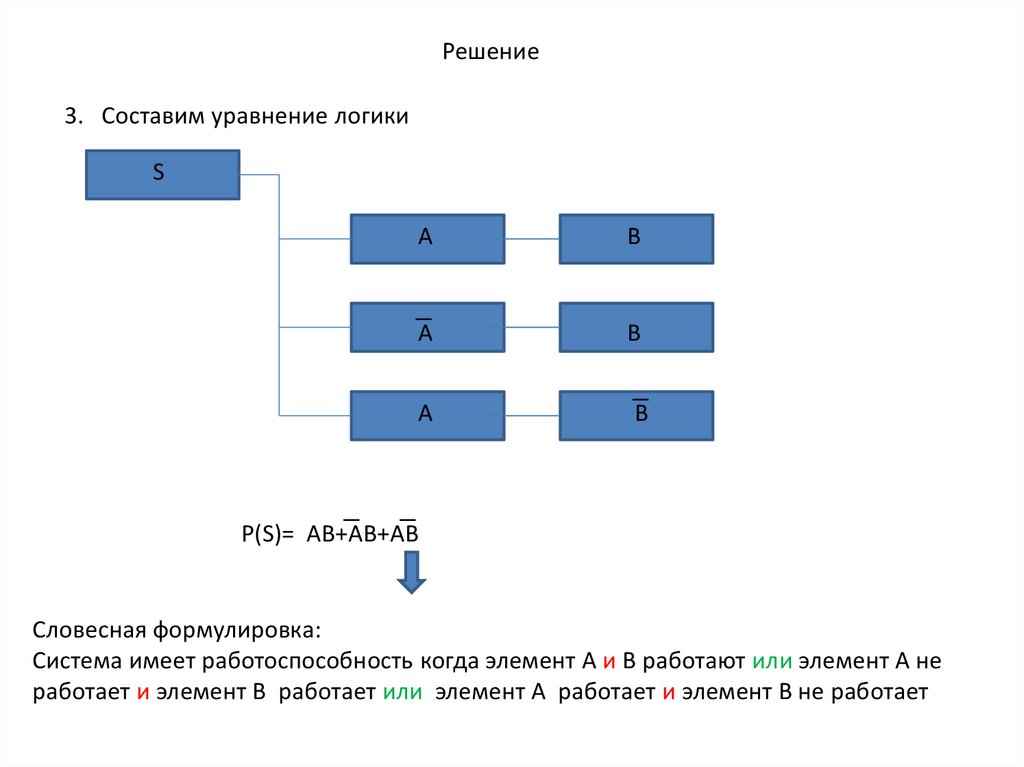
Решение3. Составим уравнение логики
S
A
B
A
B
A
B
P(S)= AB+AB+AB
Словесная формулировка:
Система имеет работоспособность когда элемент А и B работают или элемент А не
работает и элемент B работает или элемент А работает и элемент B не работает
13.
Решение3. Расписываем уравнение
P(S)= AB+AB+AB=
=P(A)*P(B) + q(A)*P(B) + P(A)*q(B)
=P(A)*P(B) + (1-P(A))*P(B) + P(A)* (1-P(B))
=0.7*0.9 + (1-0.7)*0.9 + 0.7* (1-0.9)
=0.63 + 0.27 + 0.07
= 0.97
14.
Старый метод решенияА
B
q(S)= q (A)*q(B)
q(S)= (1-P(A))*(1-P(B)) = (1-0.7)*(1-0.9) = 0.3*0.1=0.03
P(S)= 1-q(s) = 1-0.03 = 0.97
15.
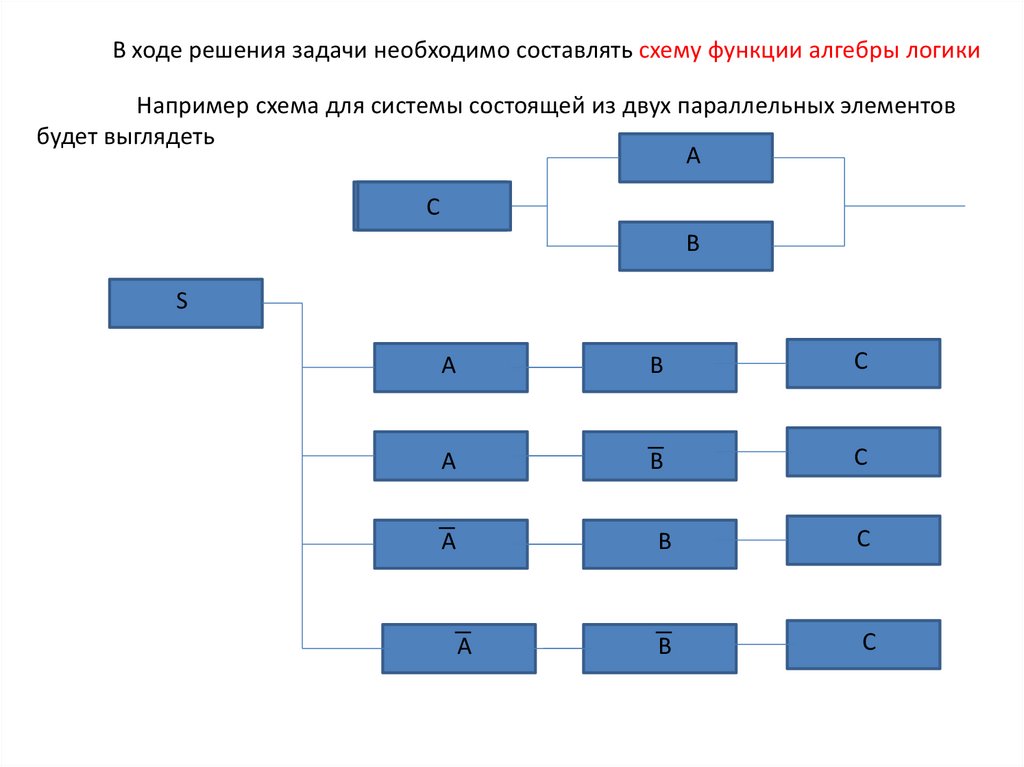
В ходе решения задачи необходимо составлять схему функции алгебры логикиНапример схема для системы состоящей из двух параллельных элементов
будет выглядеть
А
С
B
S
A
B
С
A
B
С
A
A
B
С
B
С






 mathematics
mathematics physics
physics








