Similar presentations:
Свойства функций
1.
СВОЙСТВА ФУНКЦИЙ5.09.12.
2.
Домашнее задание:§ 2 , теория в конспекте
№ 2.13.
3.
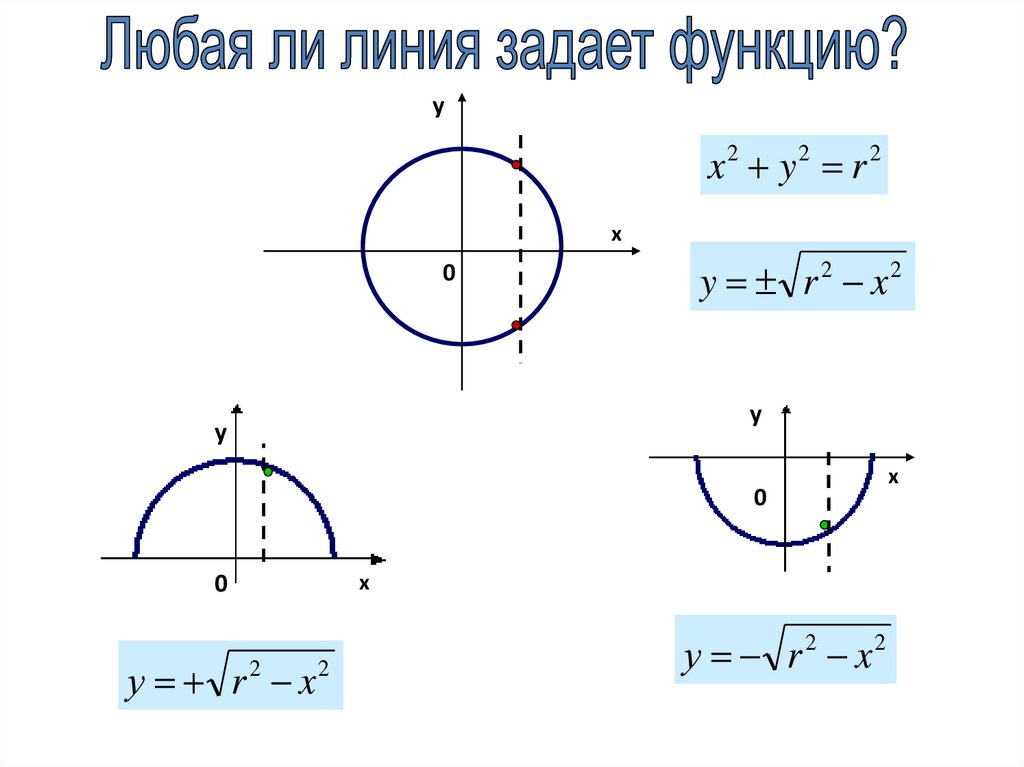
уx2 y2 r 2
x
0
y r 2 x2
у
у
0
0
у r 2 x2
x
у r 2 x2
x
4.
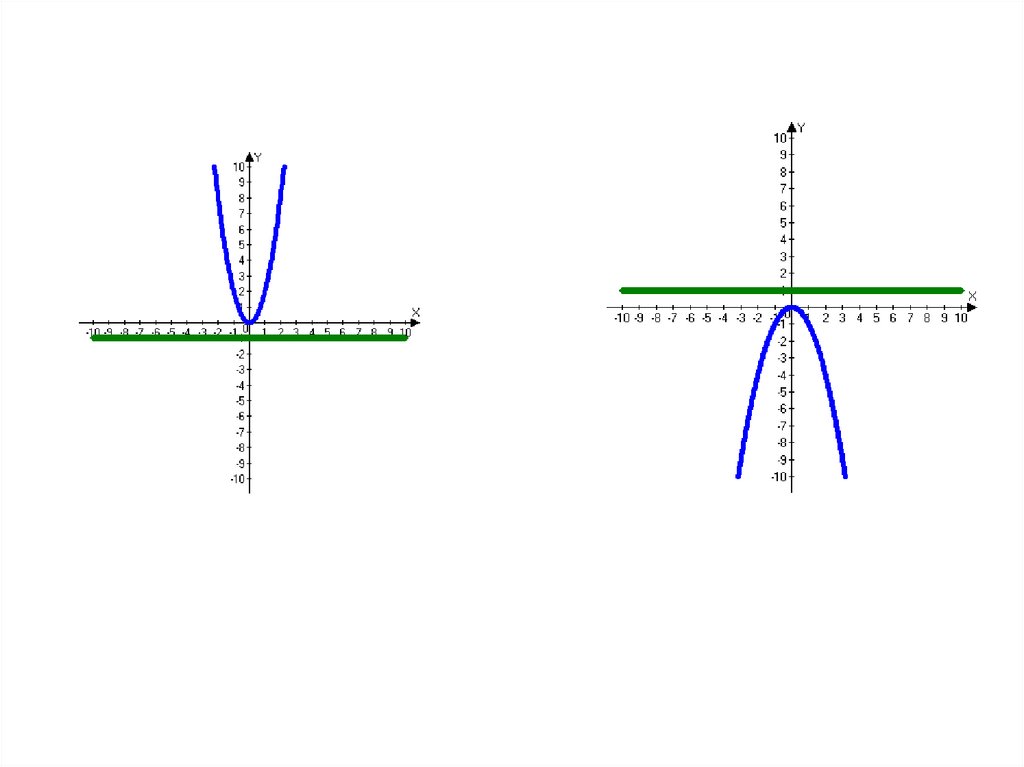
Является ли графическим заданием какой-либо функциифигура, изображенная на рисунке?
5.
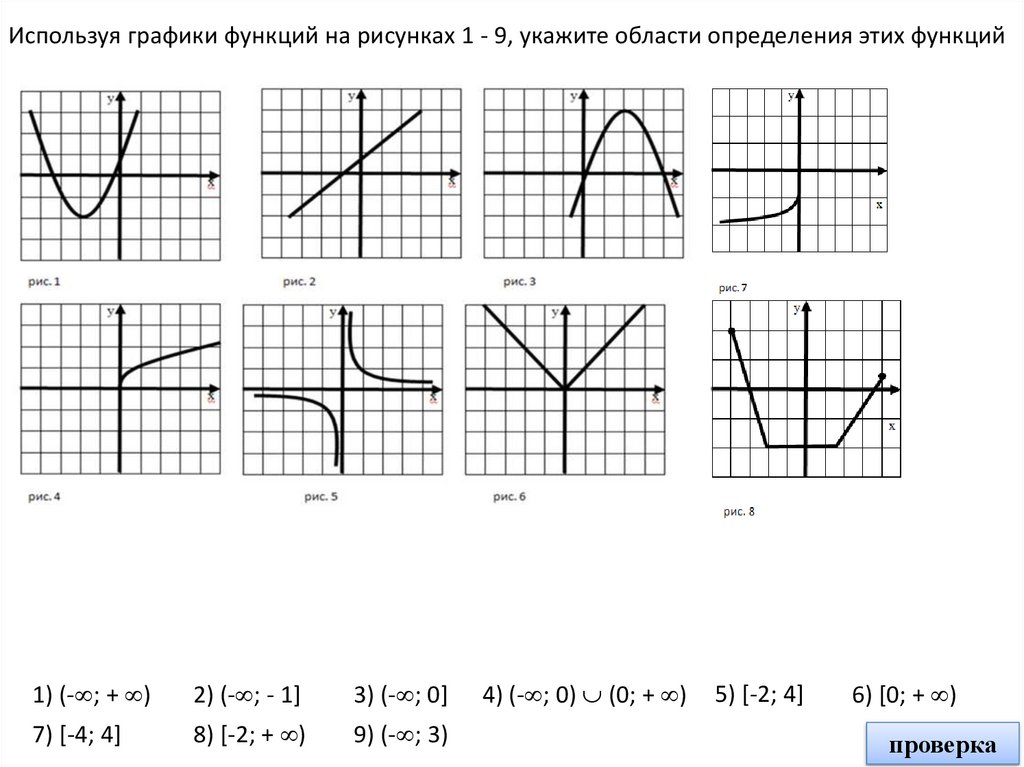
Используя графики функций на рисунках 1 - 9, укажите области определения этих функций1) (- ; + )
1) (- ; + )
6) [0; + )
4) (- ; 0) (0; + )
1) (- ; + )
2) (- ; - 1]
3) (- ; 0]
7) [-4; 4]
8) [-2; + )
9) (- ; 3)
1) (- ; + )
1) (- ; + )
4) (- ; 0) (0; + )
3) (- ; 0]
7) [-4; 4]
5) [-2; 4]
6) [0; + )
проверка
6.
СВОЙСТВА ФУНКЦИЙ5.09.12.
7.
ОПРЕДЕЛЕНИЕФункцию у = f(x) называют возрастающей
(убывающей) на множестве X Є D(f), если
для любых двух элементов x1 и х2
множества Х, таких, что x1 < x2,
выполняется неравенство
f(x1) < f(x2) ( f(x1) > f(x2)).
8.
9.
• Функция возрастает (убывает),если большему значению
аргумента соответствует
большее(меньшее) значение
функции.
10.
• Термины «возрастающая» и «убывающая»функции объединяют общим названием
монотонная функция.
• Исследование функции на возрастание или
убывание называют исследованием
функции на монотонность.
11.
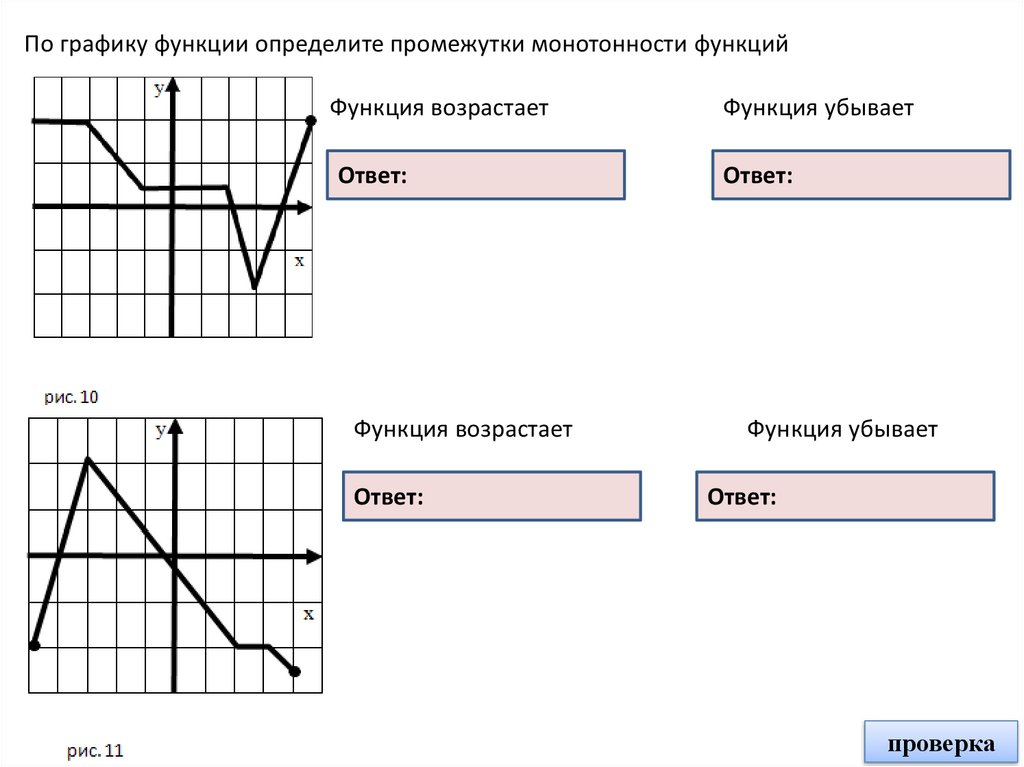
По графику функции определите промежутки монотонности функцийФункция возрастает
Ответ:
Функция убывает
Ответ:
[3; 5]
Функция возрастает
Ответ:
[- 5; - 3]
[- 3; - 2] [2; 3]
Функция убывает
Ответ:
[- 3; 2] [3; 4]
проверка
12.
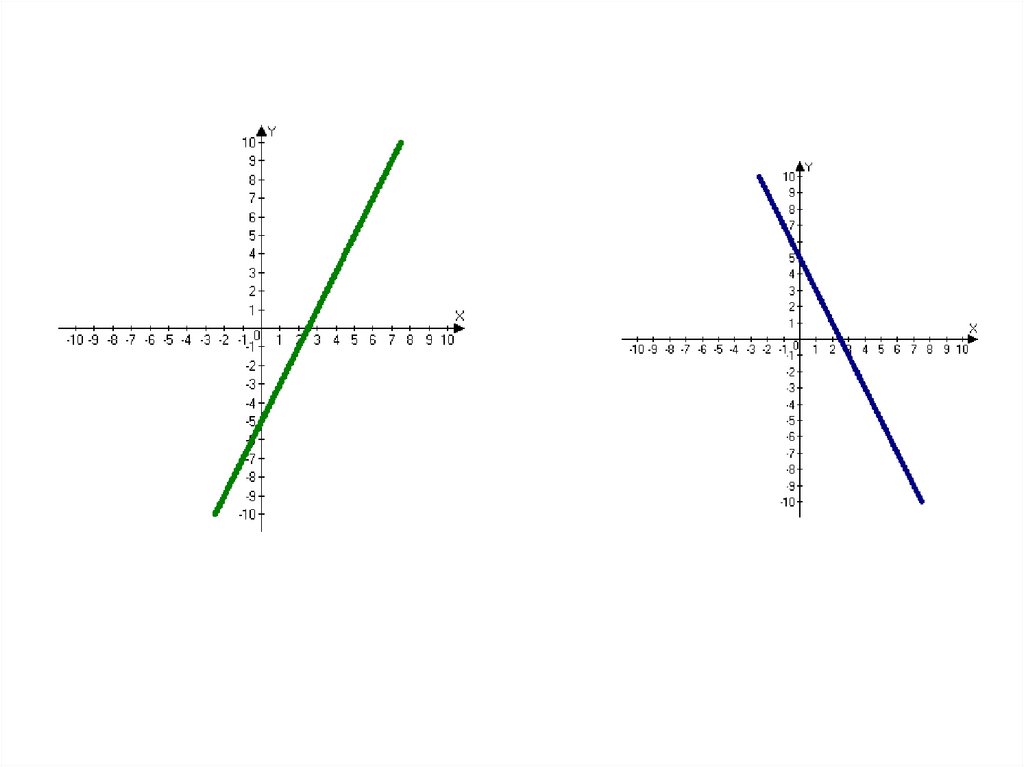
ПРИМЕР № 1.Исследовать на монотонность функцию
а) у = – 3х + 7;
б) у = х³ + 7.
13.
ОПРЕДЕЛЕНИЕ• Функция называется ограниченной
снизу на множестве X Є D(f)
(ограниченной сверху на множестве
X Є D(f)), если существует такое число
m, что для любого значения х Є D(f)
выполняется неравенство f(x) > m
(f(x) < m).
14.
15.
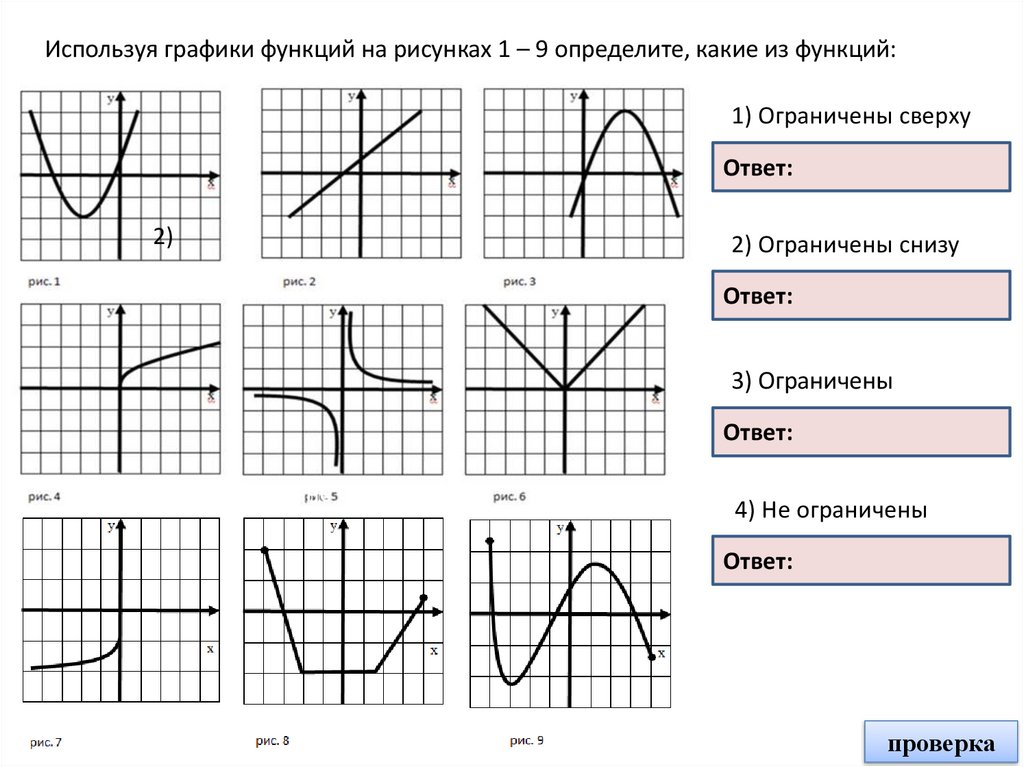
Используя графики функций на рисунках 1 – 9 определите, какие из функций:1) Ограничены сверху
Ответ:
2)
снизу
2) Ограничены снизу
не ограничена
сверху
Ответ:
3) Ограничены
Ответ:
снизу
не ограничена
снизу
4) Не ограничены
Ответ:
сверху
ограничена
ограничена
проверка
16.
ОПРЕДЕЛЕНИЕЧисло m называется наименьшим
(наибольшим) значением функции у = f(x)
на множестве X Є D(f), если:
1. Существует число x0 Є D(f) такое, что
f(x0) = M;
2. Для любого значения х Є Х выполняется
неравенство f(x) ≥ f(x0) (f(x) ≤ f(x0)).
17.
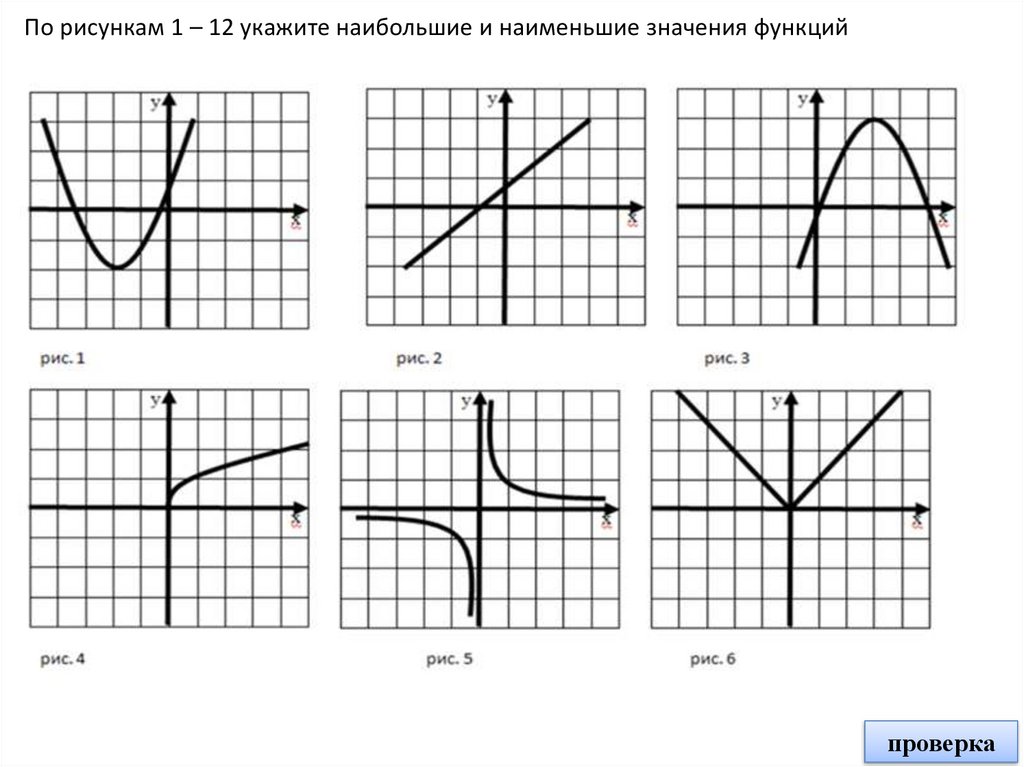
По рисункам 1 – 12 укажите наибольшие и наименьшие значения функцийУнаим = - 2
Унаим = 0
Нет Унаиб и Унаим
Нет Унаиб и Унаим
Унаиб = 3
Унаим = 0
проверка
18.
ОПРЕДЕЛЕНИЕФункция f называется чётной (нечётной),
если для любого х из ее области
определения f(-x) = f(x) (f(-x)= - f(x)).
19.
1. График четной функции симметриченотносительно оси ординат.
2. График нечетной функции
симметричен относительно начала
координат.
20.
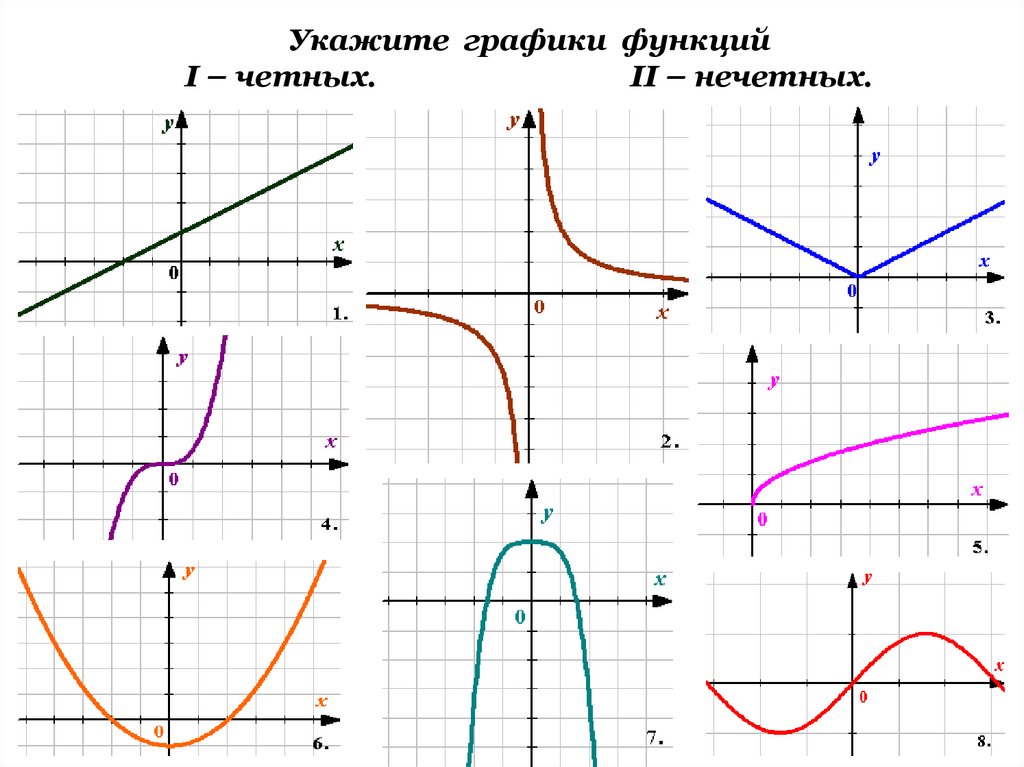
Укажите графики функцийI – четных.
II – нечетных.
21.
ПРИМЕР № 2.Исследовать на чётность функцию
а) у = 3х² + 7;
б) у = х³;
в) у = х³ + 7.
22.
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ• 1. Область определения функции D(f).
• 2. Промежутки возрастания и убывания
(монотонность) функции.
• 3. Ограниченность функции.
• 4. Наибольшее и наименьшее значения
функции.
• 5. Непрерывность функции.
• 6. Область значений функции Е(f).
• 7. Четность функции.
• 8. Выпуклость функции.














 mathematics
mathematics








