Similar presentations:
Свойства функции 11 класс
1.
Свойства функции11 класс
y = аx2 +bх +с
Автор: Драгунова С.А.,
учитель математики
МБОУ СОШ № 19,
г. Заполярный
Мурманской области
2.
ОглавлениеI. Свойства функции
1. Область определения функции
2. Множество значений функции
3. Ограниченность функции
4. Наименьшее значение функции
5. Наибольшее значение функции
6. Четность функции
7. Нечетность функции
8. Возрастание функции
9. Убывание функции
II. Самостоятельная работа
Выход
3.
Область определения: D(y)1
Областью определения функции y = f(x) называют множество
всех действительных значений независимой переменной х, для
каждого из которых функция принимает действительные
значения.
Примеры
a
D(y)
b
y = f(x)
Оглавление
D(y) =[a;b]
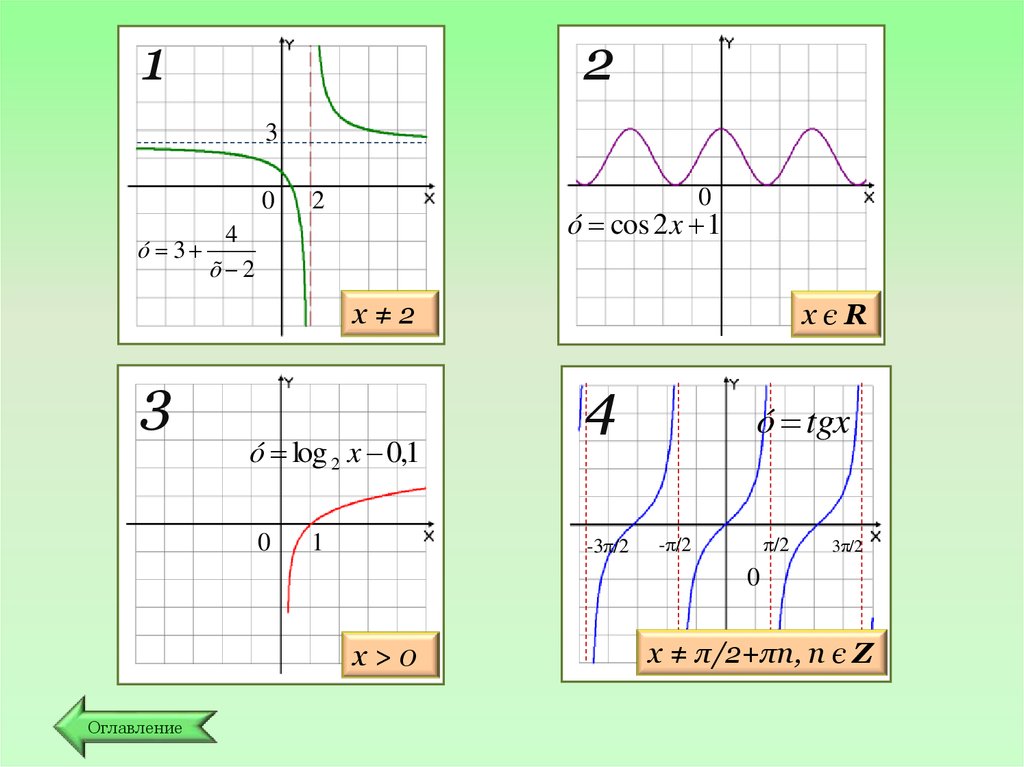
4.
21
3
0
0
2
ó cos 2 x 1
4
ó 3
õ 2
х≠2
3
ó log 2 x 0,1
0
1
хєR
4
-3π/2
ó tgx
π/2
-π/2
3π/2
0
х>0
Оглавление
х ≠ π/2+πn, n є Z
5.
Множество значений: E(y)2
Множеством значений (областью значений) функции y = f(x)
называют множество всех чисел f(x), соответствующих каждому
х из области определения функции.
d
E(y)
Примеры
E(y) = [c;d]
c
y = f(x)
Оглавление
6.
21
2
3
0
2
0
ó cos 2 x 1
4
ó 3
õ 2
y≠3
3
ó log 2 x 0,1
у є [0;2]
4
-3π/2
0
1
π/2
-π/2
3π/2
0
yєR
Оглавление
ó tgx
yєR
7.
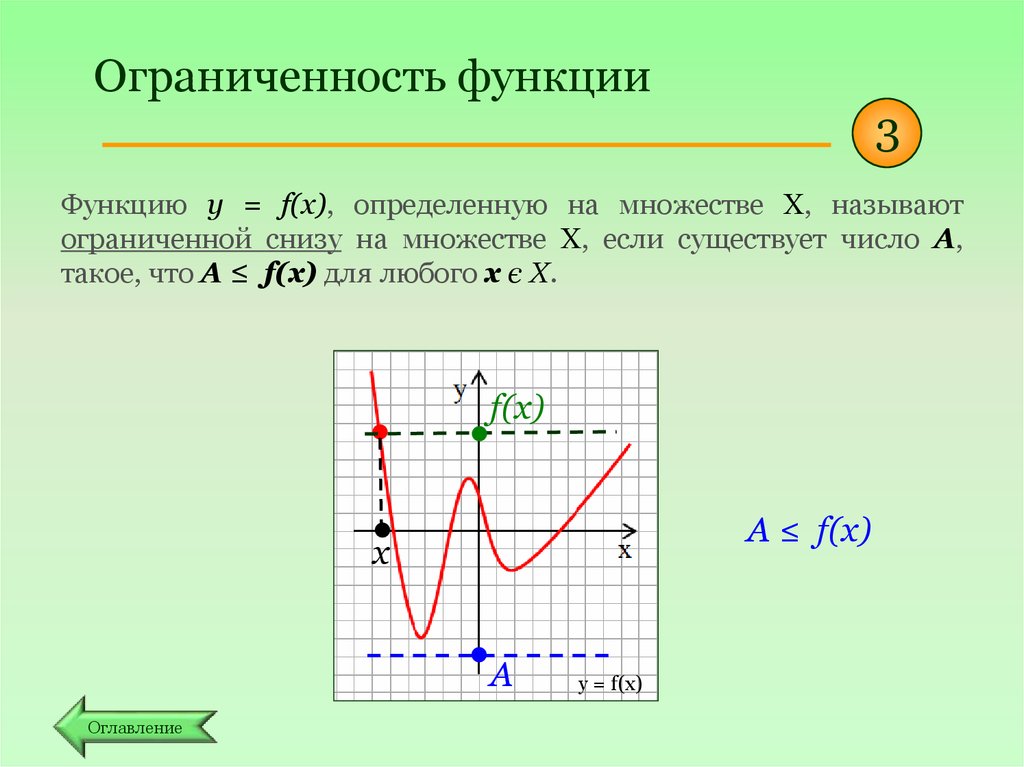
Ограниченность функции3
Функцию y = f(x), определенную на множестве Х, называют
ограниченной снизу на множестве Х, если существует число А,
такое, что А ≤ f(x) для любого х є Х.
f(x)
А ≤ f(x)
x
A
Оглавление
y = f(x)
8.
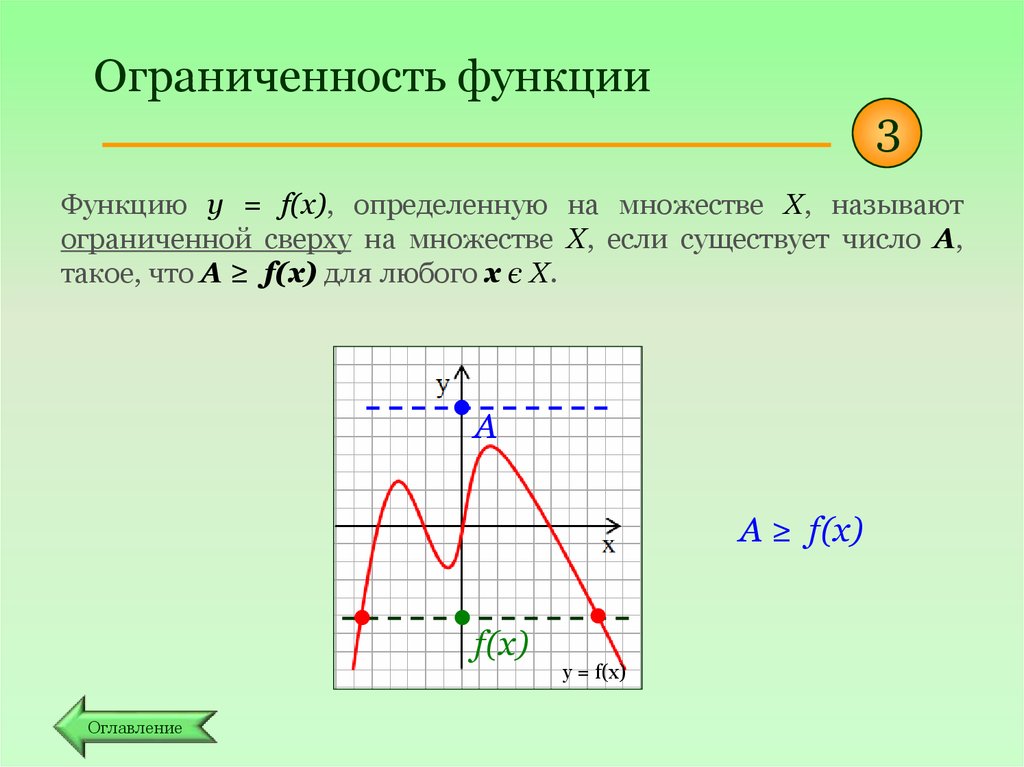
Ограниченность функции3
Функцию y = f(x), определенную на множестве Х, называют
ограниченной сверху на множестве Х, если существует число А,
такое, что А ≥ f(x) для любого х є Х.
A
А ≥ f(x)
f(x)
Оглавление
y = f(x)
9.
Ограниченность функции3
Функцию y = f(x), определенную на множестве Х, называют
ограниченной на множестве Х, если существует число M > 0,
такое, что |f(x)| ≤ M для любого х є Х.
y = f(x)
M
f(x)
Примеры
-M
Оглавление
-M≤ f(x) ≤ M
10.
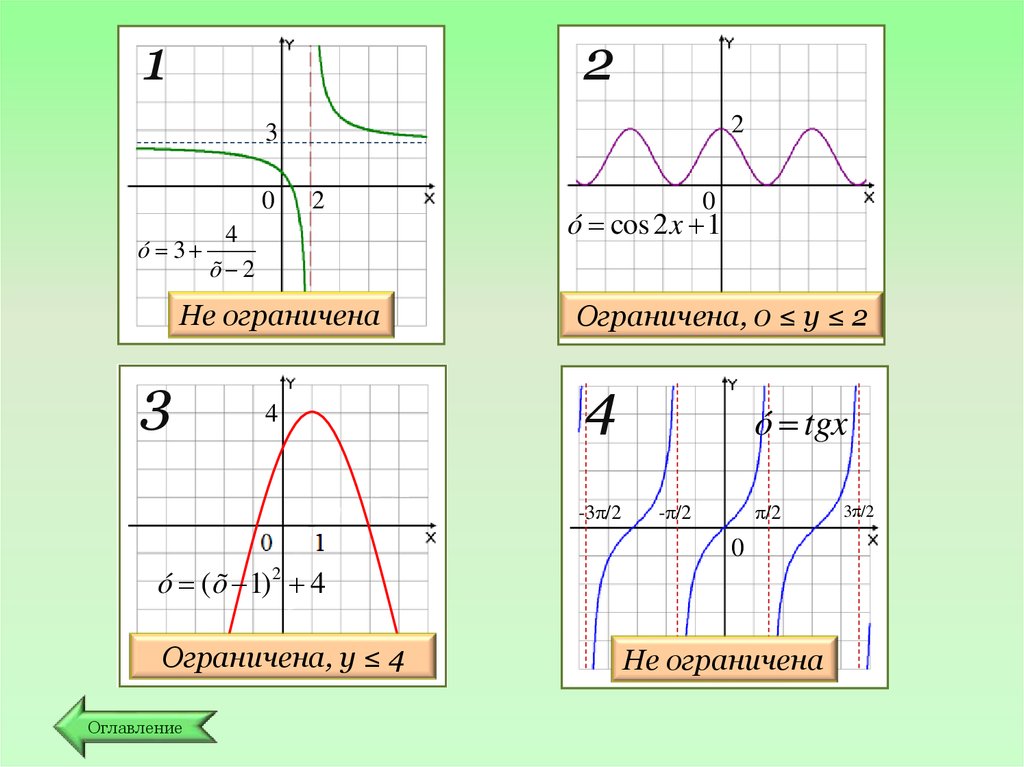
21
2
3
0
2
4
ó 3
õ 2
Не ограничена
3
4
0
ó cos 2 x 1
Ограничена, 0 ≤ y ≤ 2
4
-3π/2
ó tgx
π/2
-π/2
0
ó ( õ 1) 2 4
Ограничена, y ≤ 4
Оглавление
Не ограничена
3π/2
11.
Наименьшее значение функции4
Функция y = f(x) принимает на множестве Х
наименьшее
значение в точке х0, если х0 є Х и f(x0) ≤ f(x) для любого х є Х.
y = f(x)
f(x)
x0
f(x0) ≤ f(x)
x
f(x0)
Оглавление
12.
Наибольшее значение функции5
Функция y = f(x) принимает на множестве Х
наибольшее
значение в точке х0, если х0 є Х и f(x0) f(x) для любого х є Х.
f(x0)
Примеры
x
f(x)
y = f(x)
Оглавление
x0
f(x0) f(x)
13.
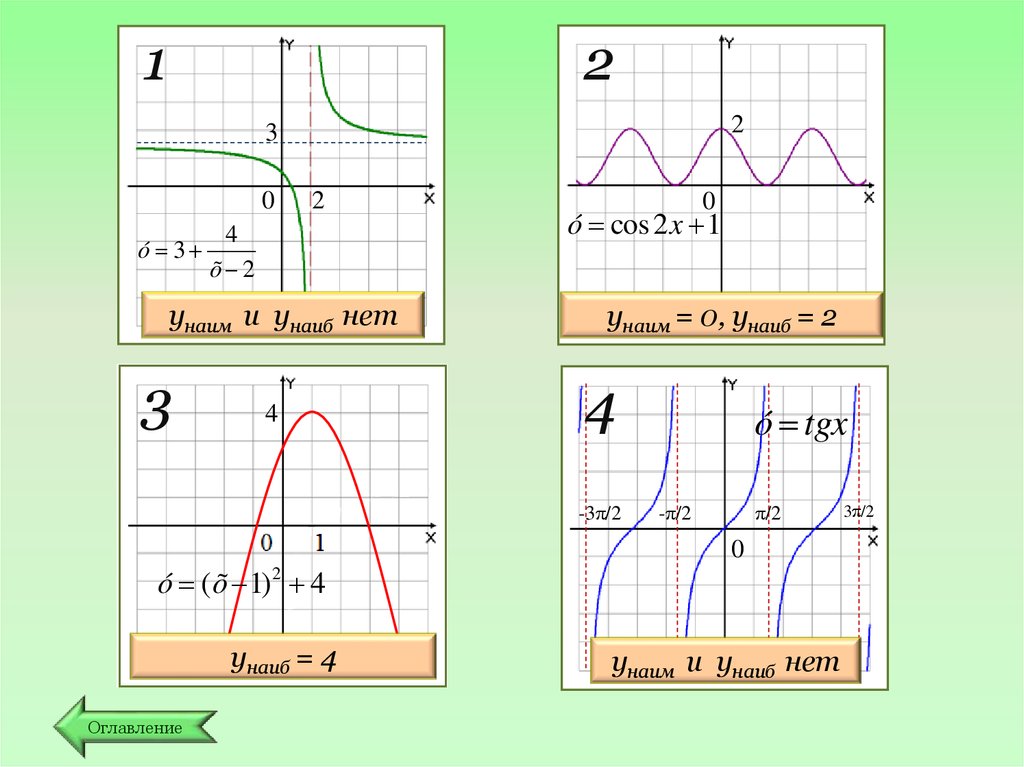
21
2
3
0
2
4
ó 3
õ 2
унаим и унаиб нет
3
4
0
ó cos 2 x 1
унаим = 0, унаиб = 2
4
-3π/2
ó tgx
π/2
-π/2
0
ó ( õ 1) 2 4
унаиб = 4
Оглавление
унаим и унаиб нет
3π/2
14.
Четность функции6
Функцию y = f(x) с областью определения Х называют четной,
если для любого х є Х число (- х) є Х и справедливо равенство
f(-x) = f(x).
f(-x)
-x
f(x)
x
y = f(x)
Оглавление
f(- x) = f(x)
15.
Нечетность функции7
Функцию y = f(x) с областью определения Х называют нечетной,
если для любого х є Х число (- х) є Х и справедливо равенство
f(-x) = - f(x).
f(-x)
x
Примеры
f(- x) = - f(x)
-x
f(x)
y = f(x)
Оглавление
16.
21
2
3
0
2
4
ó 3
õ 2
0
ó cos 2 x 1
Ни четная, ни нечетная
3
ó log 2 x 0,1
Четная
4
-3π/2
0
1
Ни четная, ни нечетная
Оглавление
ó tgx
π/2
-π/2
0
Нечетная
3π/2
17.
Возрастание функции8
Функцию y = f(x), определенную на множестве Х, называют
возрастающей на этом промежутке, если для любой пары чисел х1
и х2 из этого промежутка из неравенства
х1 х2 следует
неравенство f(x1) f(x2).
f(x2)
x1
x2
f(x1)
y = f(x)
Оглавление
f(x1) f(x2)
18.
Убывание функции9
Функцию y = f(x), определенную на множестве Х, называют
убывающей на этом промежутке, если для любой пары чисел х1 и
х2 из этого промежутка из неравенства
х1 х2 следует
неравенство f(x1) > f(x2).
f(x1)
Примеры
x2
x1
f(x2)
y = f(x)
Оглавление
f(x1) > f(x2)
19.
12
3
0
ó 3
ó ( õ 1) 2 4
2
4
õ 2
(-∞;1] ,
(-∞;2) U (2;+∞)
3
ó log 2 x 0,1
0
1
(0;+∞)
[1;+∞)
4
-3π/2
Оглавление
4
ó tgx
π/2
-π/2
3π/2
0
(-π/2 +πn;π/2 +πn), n є N
20.
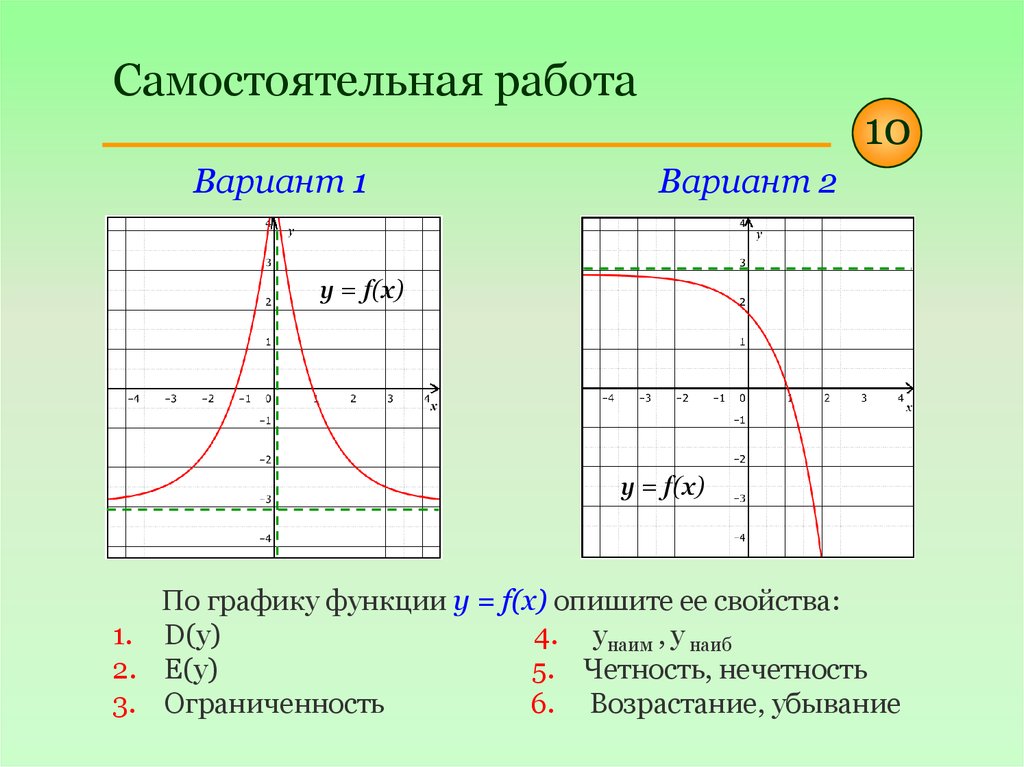
Самостоятельная работаВариант 1
10
Вариант 2
y = f(x)
y = f(x)
По графику функции y = f(x) опишите ее свойства:
1. D(у)
4. унаим , у наиб
2. E(y)
5. Четность, нечетность
3. Ограниченность
6. Возрастание, убывание
21.
ОтветыВариант 1
1.
2.
3.
4.
5.
6.
D(y)=(-∞;0)U(0;+∞)
Е(у)=(-3;+∞)
Ограничена снизу
унаим , у наиб нет
Четная
на (-∞;0),
на
(0;+∞)
Оглавление
Вариант 2
1.
2.
3.
4.
5.
D(y)=(-∞;+∞)
Е(у)=(-∞;3)
Ограничена сверху
унаим , у наиб нет
Ни
четная,
ни
нечетная
6.
на всей D(y)
Выход
22.
ЛитератураУчебник для общеобразовательных учреждений
базовый и профильный уровни «Алгебра и
начала математического анализа» 11 класс ,
С.М.
Никольский,
М.К
Потапов,
Н.Н.
Решетников, А.В. Шевкин.
Оглавление
















 mathematics
mathematics








