Similar presentations:
Кривые второго порядка
1. Кривые второго порядка.
2.
Общее уравнение кривойвторого порядка имеет вид
Ах Вху Су Dх Еу F 0.
2
2
3.
Уравнениетакого
вида
может
определять:
эллипс (в частности,
окружность),
гиперболу,
параболу,
пару
прямых
(параллельных,
пересекающихся либо совпадающих),
точку или не определять никакой линии.
4. Окружность
• Окружностью наз-ся множество точекплоскости, равноудаленных от одной и
тойже точки плоскости, называемой
центром окружности.
x x y y
2
0
2
0
R
2
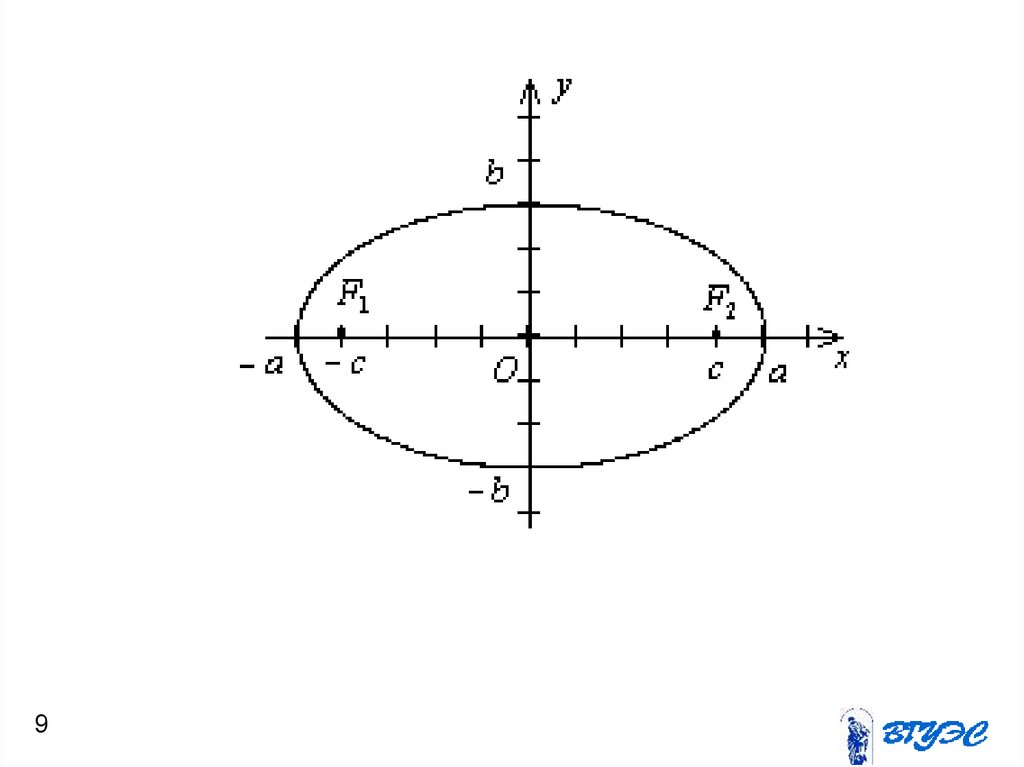
5. Эллипс
Эллипсом называется геометрическоеместо точек (плоскости), сумма
расстояний которых от двух данных
точек, называемых фокусами этого
эллипса, есть величина постоянная.
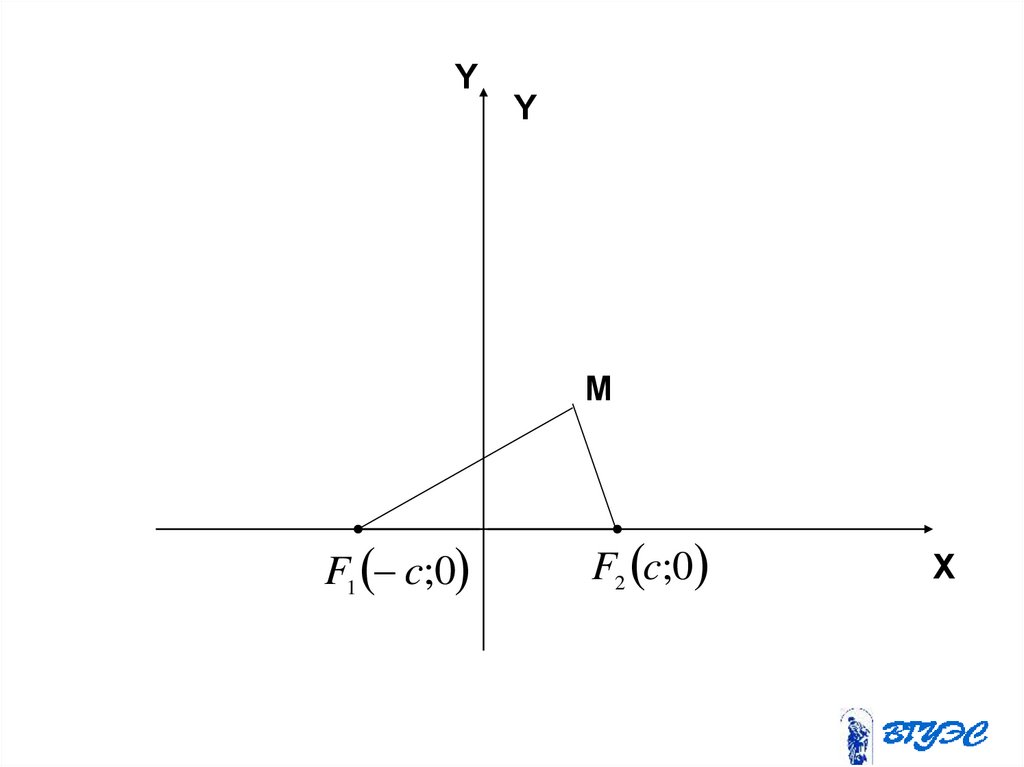
6.
YY
M
F1 c;0
F2 c;0
X
7.
MF1 MF2 2ax c
2
y
2
x c
2
a b 0
c a b
2
2
y 2a
2
8. Уравнение эллипса
ху
1
.
2
2
а
в
2
2
(x x ) ( y y )
1
a
b
2
2
0
2
0
2
9.
910. Гипербола
Гиперболой называется геометрическоеместо точек, для которых абсолютная
величина разности расстояний до двух
данных точек плоскости, называемых
фокусами, есть величина постоянная
11.
YY
M
F1 c;0
F2 c;0
X
12.
MF1 MF2 2ax c
2
x c
2
2
y
y
2
2
x c
y 2a
2
x c
y 2a
c a b
2
2
2
2
13. Уравнение гиперболы
ху
1
.
2
2
а
в
2
2
(x x ) ( y y )
1
a
b
2
2
0
2
0
2
14.
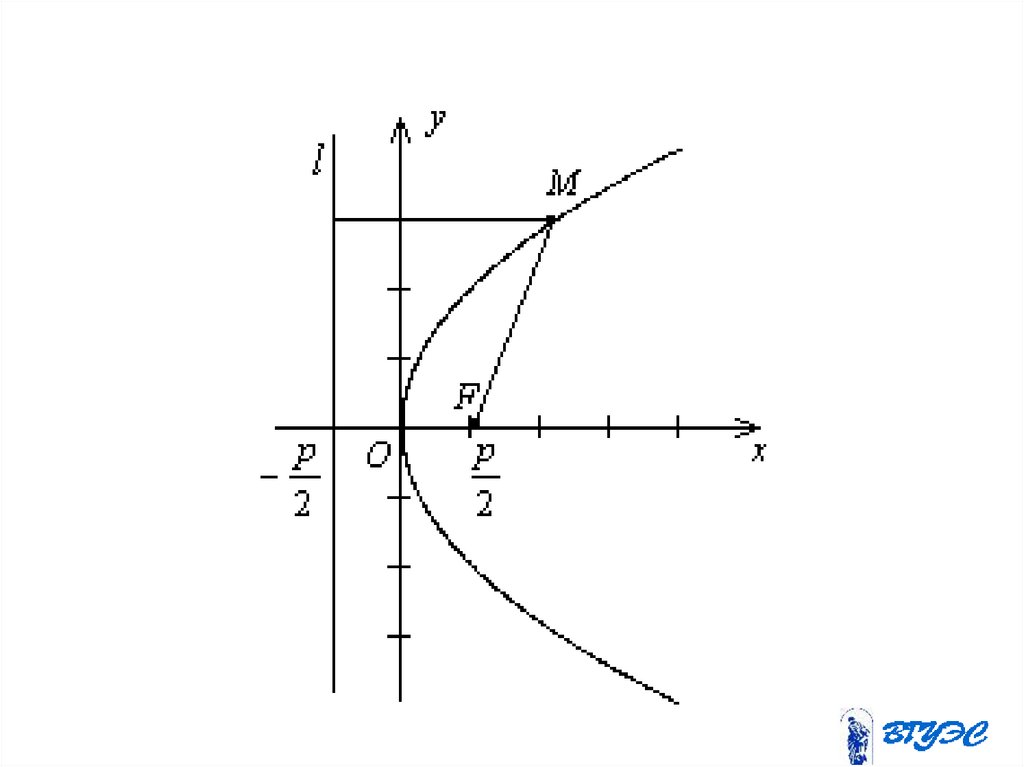
15. Парабола
Параболой называется геометрическоеместо точек, равноудаленных от данной
точки плоскости, называемой фокусом,
и данной прямой, называемой директрисой .
16.
YN
p
2
M
p
F ;0
2
X
17. Уравнение параболы
у 2 рх p 02
( y y ) 2 p( x x )
2
0
0
18.
19. Полярные координаты
х cos , у sin ;cos
x
2
х у
2
, sin
у
2
х у
2






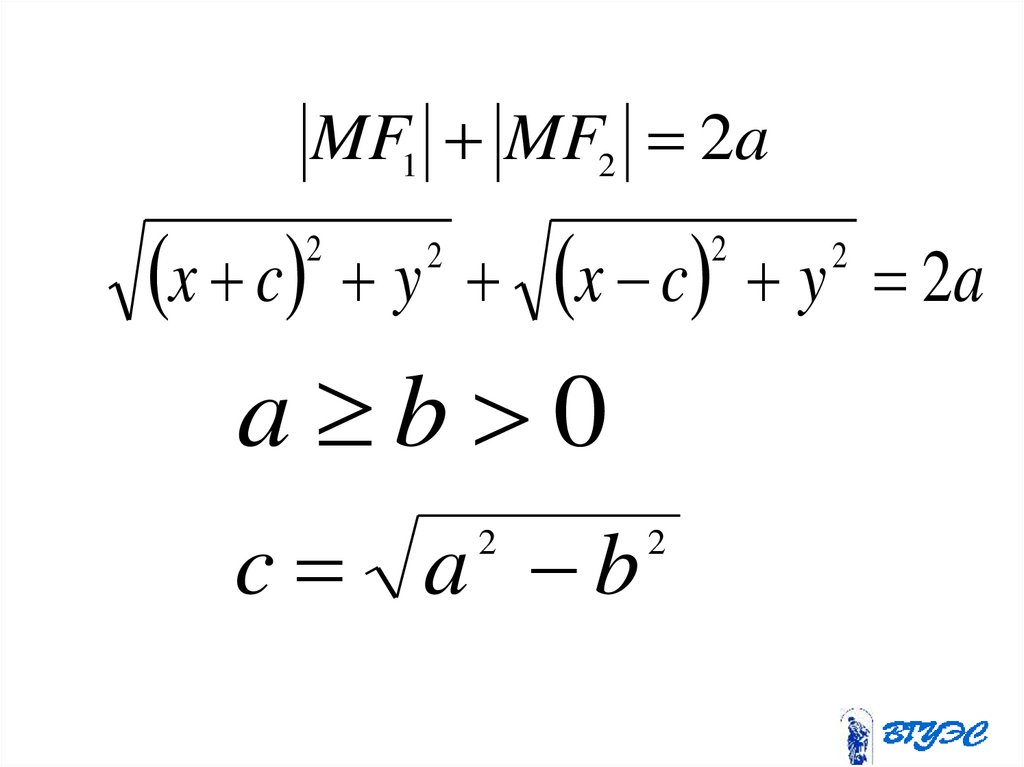


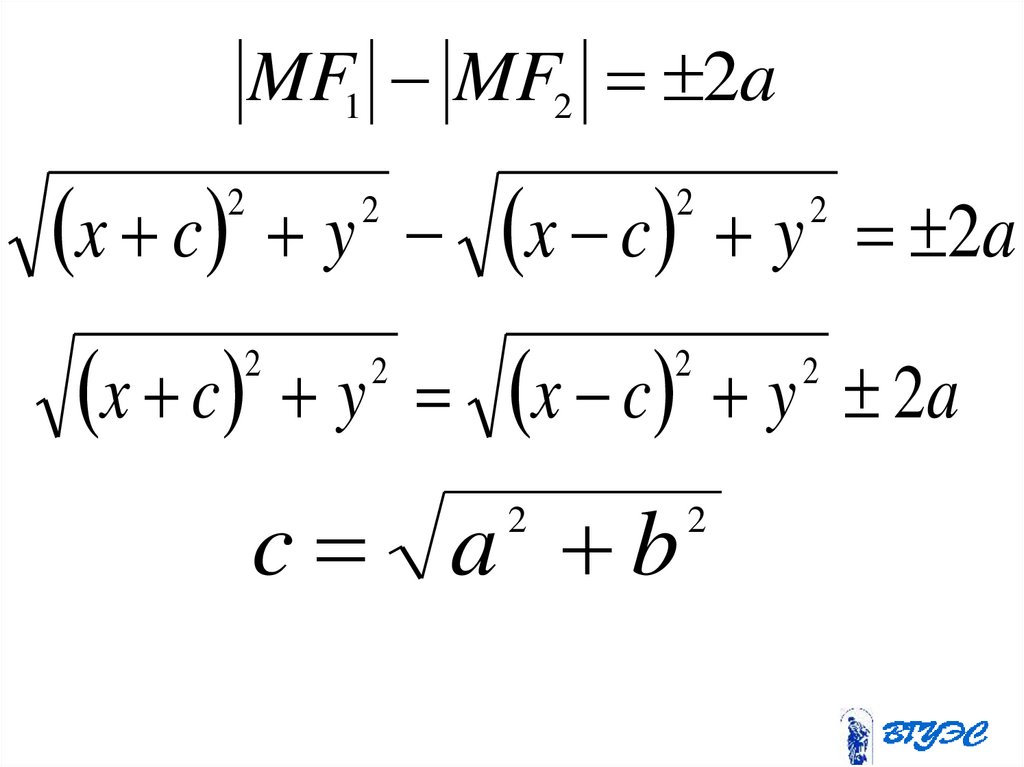




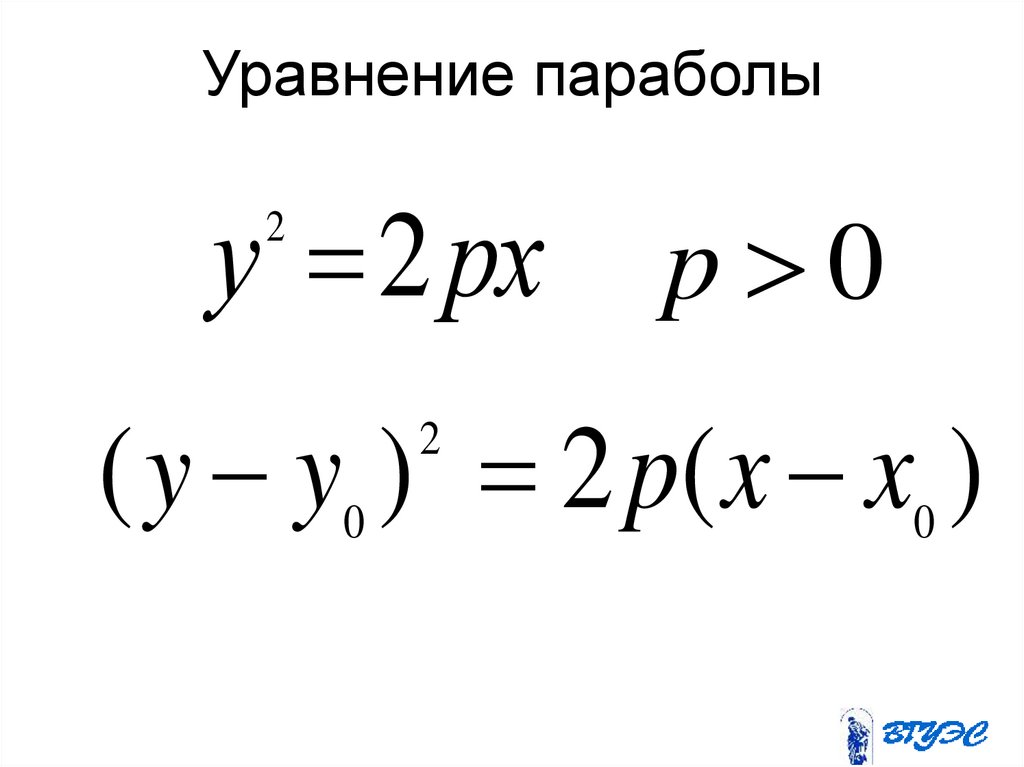

 mathematics
mathematics








