Similar presentations:
Методы решения систем уравнения
1.
2.
Решите систему уравненийx 2 y 2 25,
xy 12.
1 – графическим методом
2 – методом алгебраического сложения
3 – методом подстановки
3.
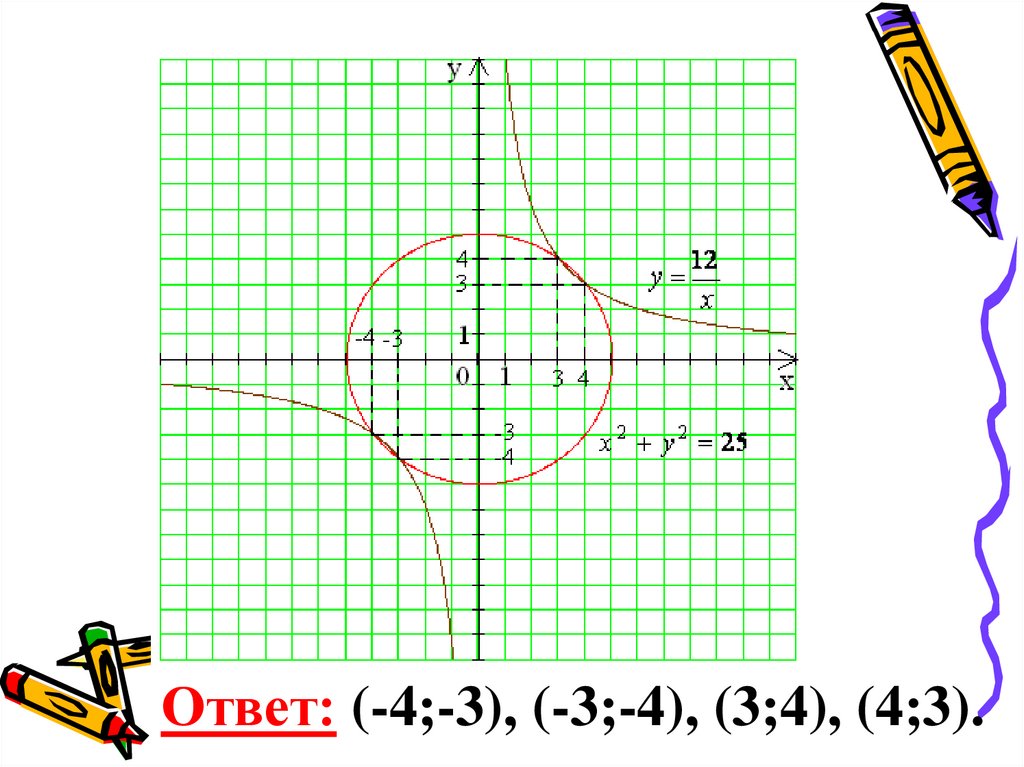
1. Графический методx y 25 - окружность с центром
(0; 0) и радиусом 5.
2
2
12 - обратная
y
x пропорциональность, график гипербола, ветви расположены
в 1 и 3 координатных
четвертях.
4.
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).5.
2. Метод алгебраического сложения2
2
2
( x y ) 49,
x y 25,
xy 12.
xy
12
.
x y 25,
xy 12 2
2
2
+
х² + 2ху + у² = 49
x y 7,
xy 12.
или
x y 7,
xy 12.
6.
x y 7,xy 12.
x 7 y
(7 y ) y 12
у² – 7у + 12 = 0
y 7 y 12 0
2
D 49 48 1
7 1
y1
4
2
7 1
y2
3
2
x 3
x 4
или
y 4
y 3
7.
x y 7,xy 12.
x 7 y
( 7 y ) y 12
у² + 7у + 12 = 0
y 7 y 12 0
2
D 49 48 1
7 1
y1
4
2
7 1
y2
3
2
x 3
x 4
или
y 4
y 3
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
8.
3. Метод подстановкиx 2 y 2 25,
xy 12.
144
2
y
25
,
y2
12
x
y
| · у²
9.
y 25 y 144 04
2
Пусть y t , тогда
2
t 25t 144 0
2
D 625 576 49
25 7
25 7
t1
16, t 2
9
2
2
10.
y 25 y 144 04
2
Пусть y t , тогда
2
t≥0
t 25t 144 0
2
D 625 576 49
25 7
25 7
t1
16, t 2
9
2
2
11.
y 25 y 144 04
2
Пусть y t , тогда
2
t≥0
t 25t 144 0
2
D 625 576 49
25 7
25 7
t1
16, t 2
9
2
2
12.
y 25 y 144 04
2
Пусть y t , тогда
2
t≥0
t 25t 144 0
2
D 625 576 49
25 7
25 7
t1
16, t 2
9
2
2
13.
y 25 y 144 04
2
Пусть y t , тогда
2
t≥0
t 25t 144 0
2
D 625 576 49
25 7
25 7
t1
16, t 2
9
2
2
14.
y 162
y1, 2 4
y 9
2
или
x 3
x 4
или
y 4
y 3
y3, 4 3
x 4
x 3
или
y 3
y 4
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
15.
Метод введенияновой переменной
16.
17.
х²у² = (ху)²Замена: ху = t,
или
18.
19.
,,
,
20.
Домашняя работаЗаписать решение
следующей системы
уравнений и изучить как
делать замены в различных
системах уравнений,
представленных в таблице



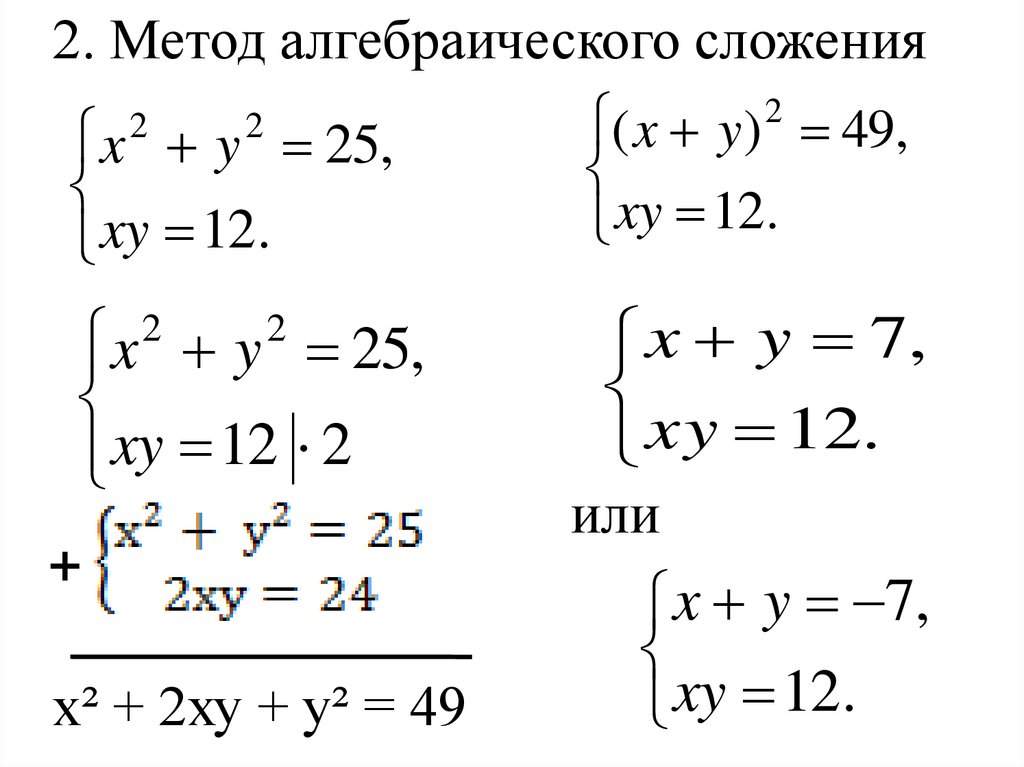
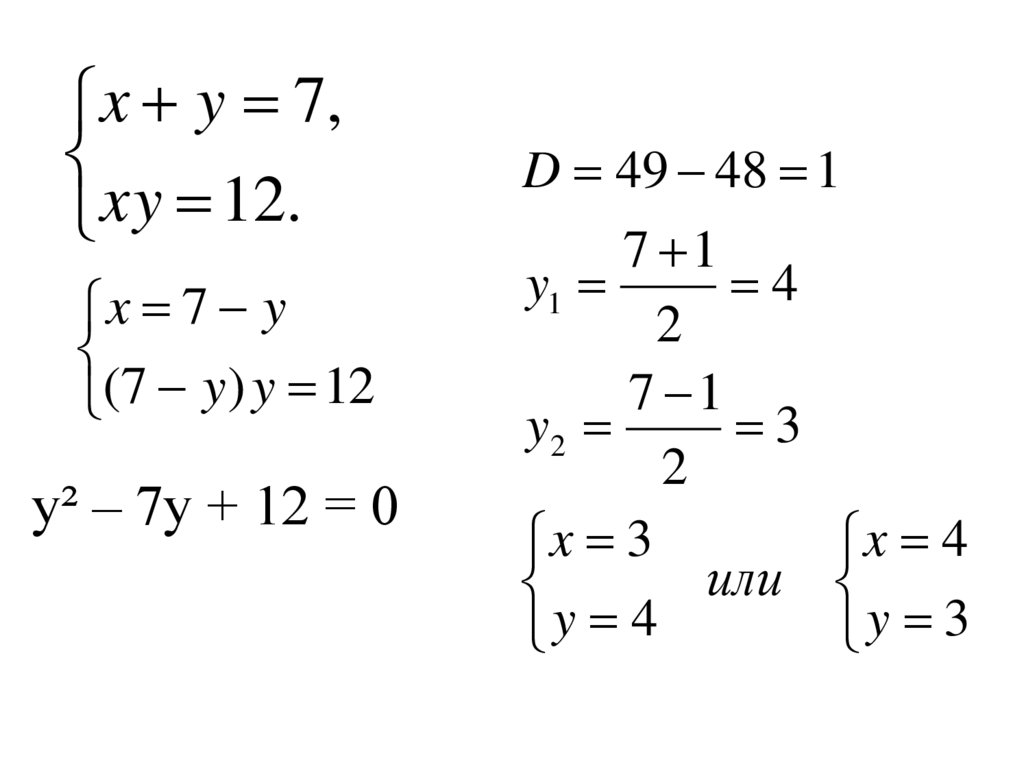


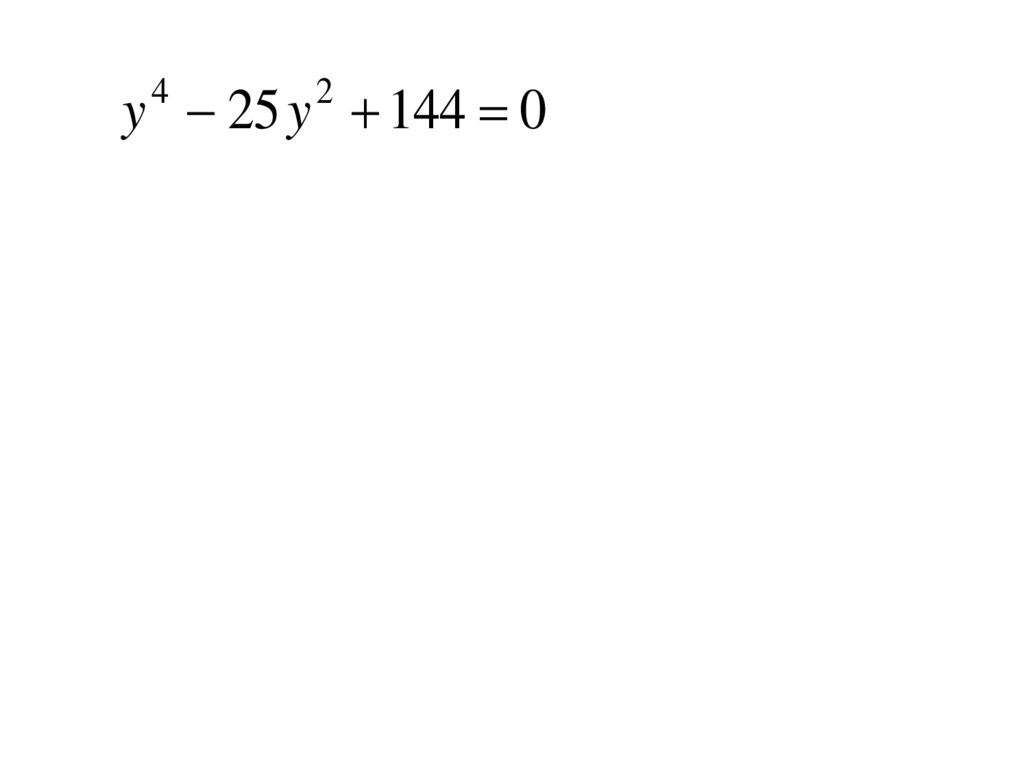
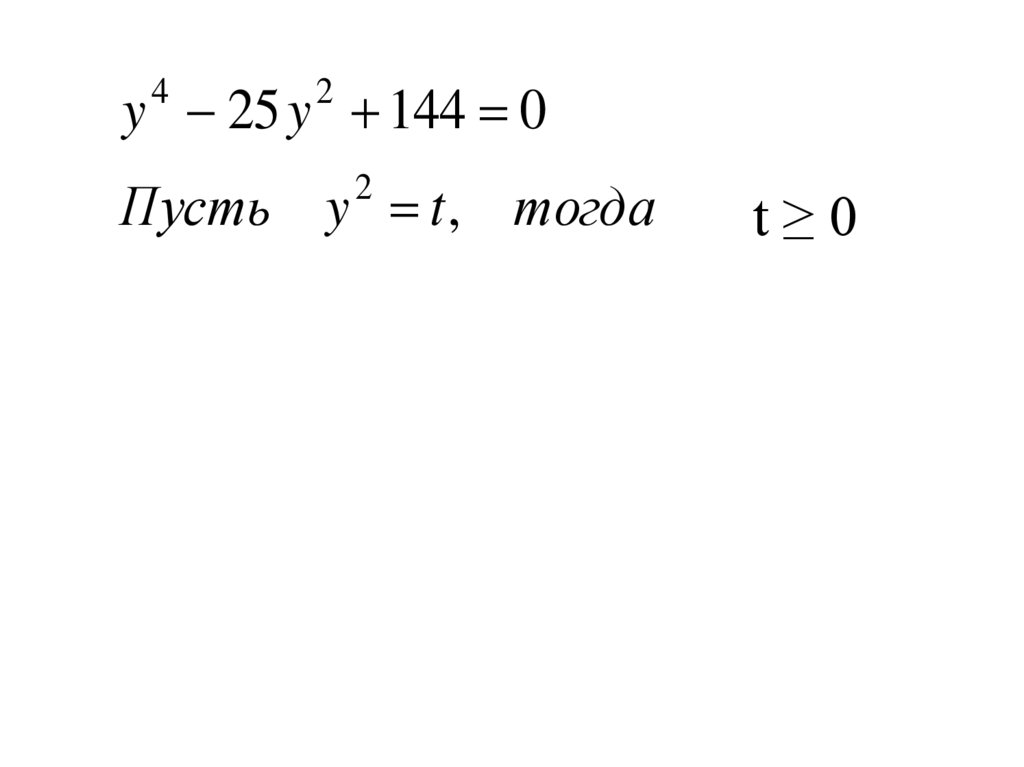
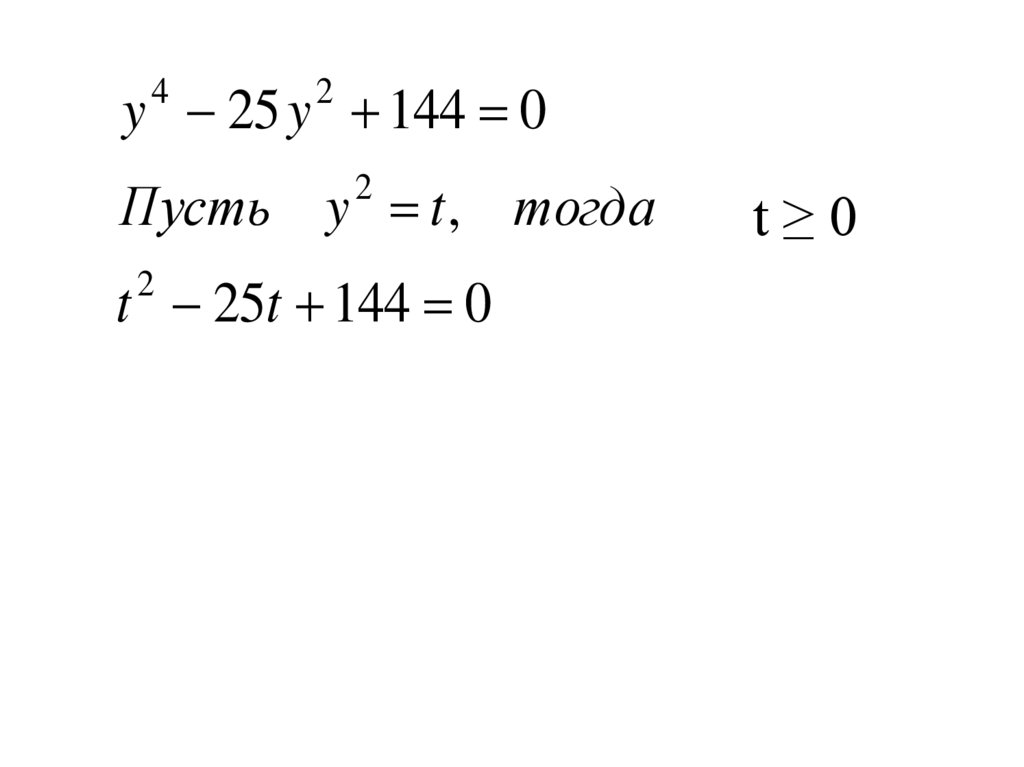
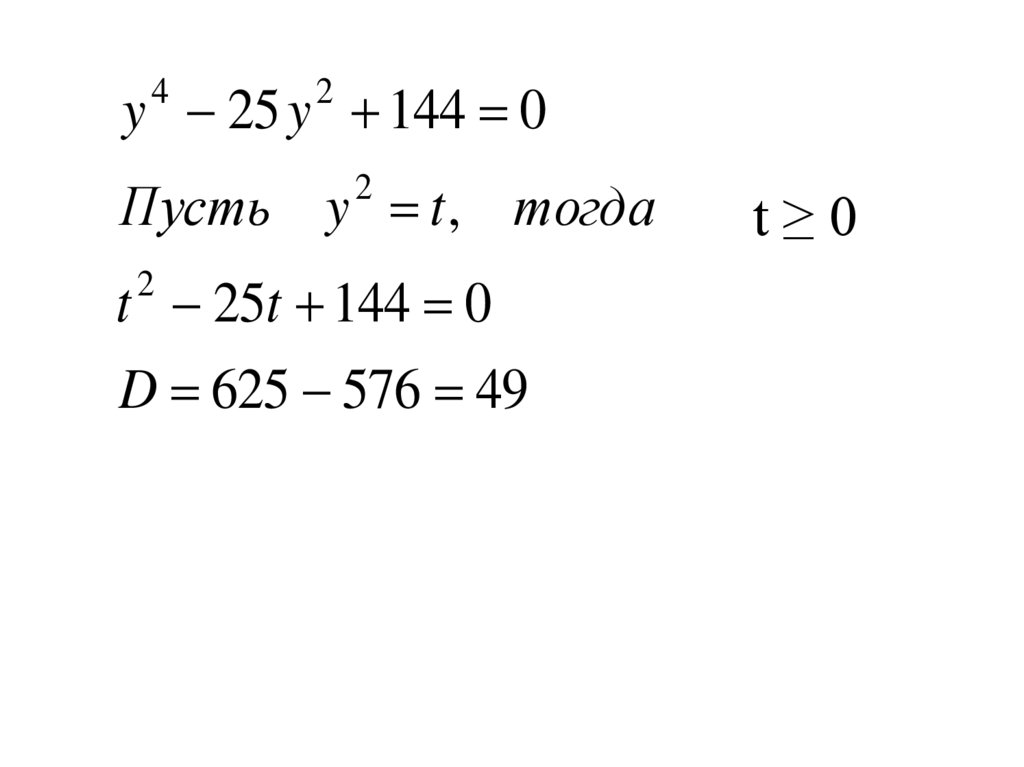
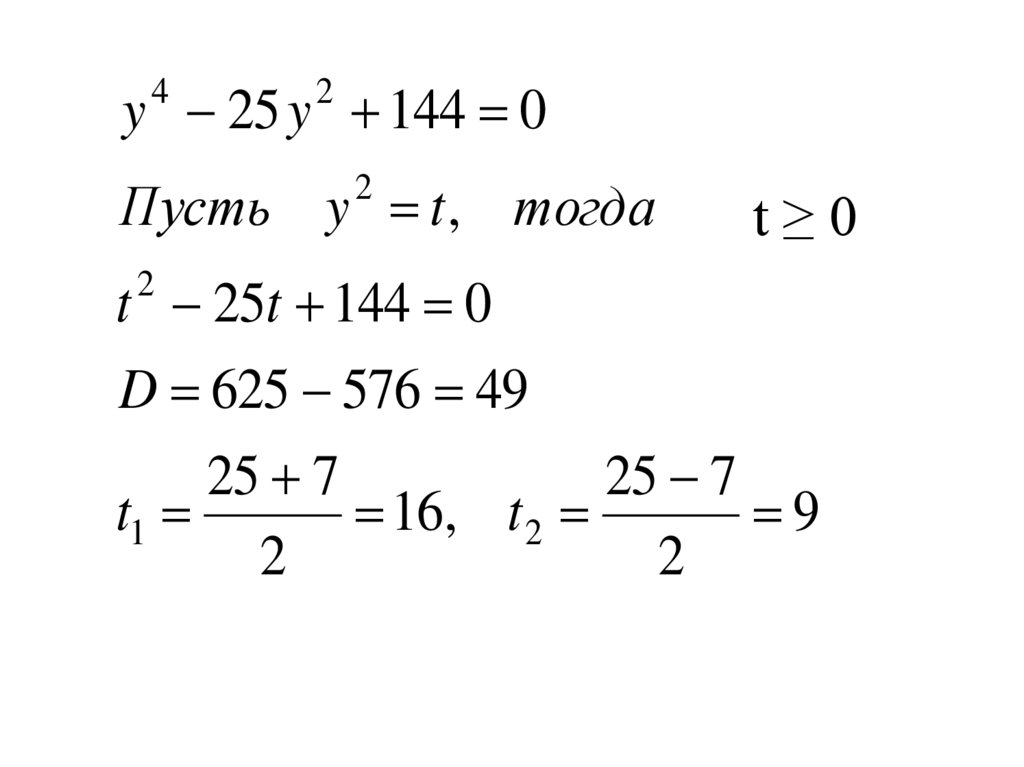


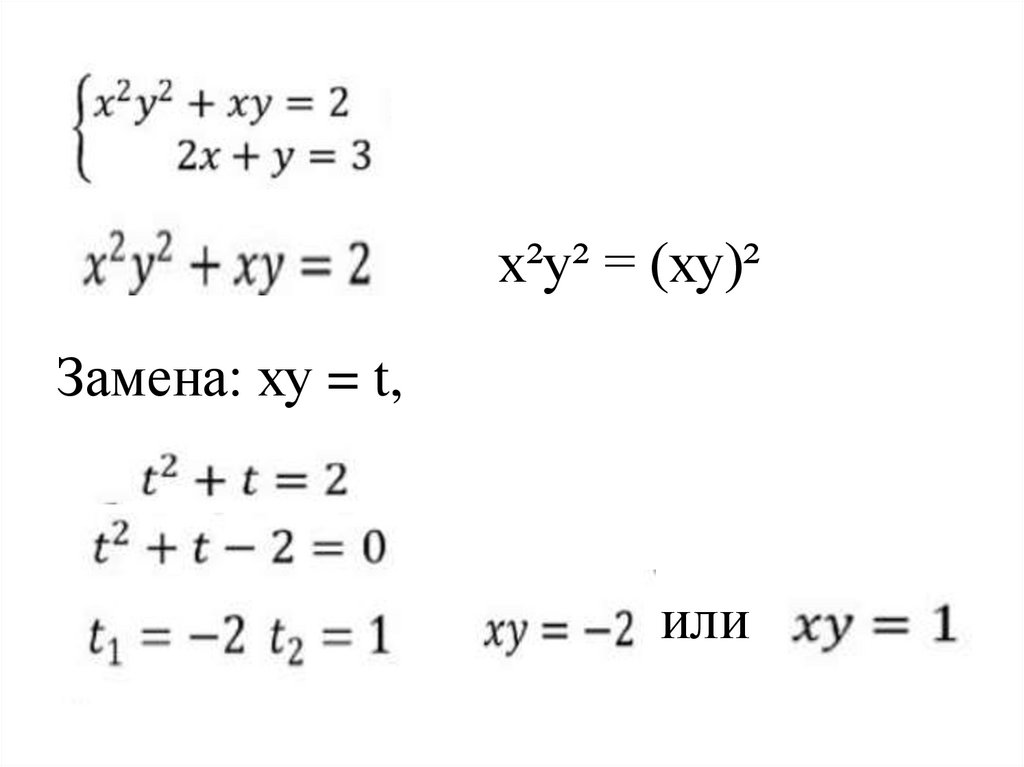

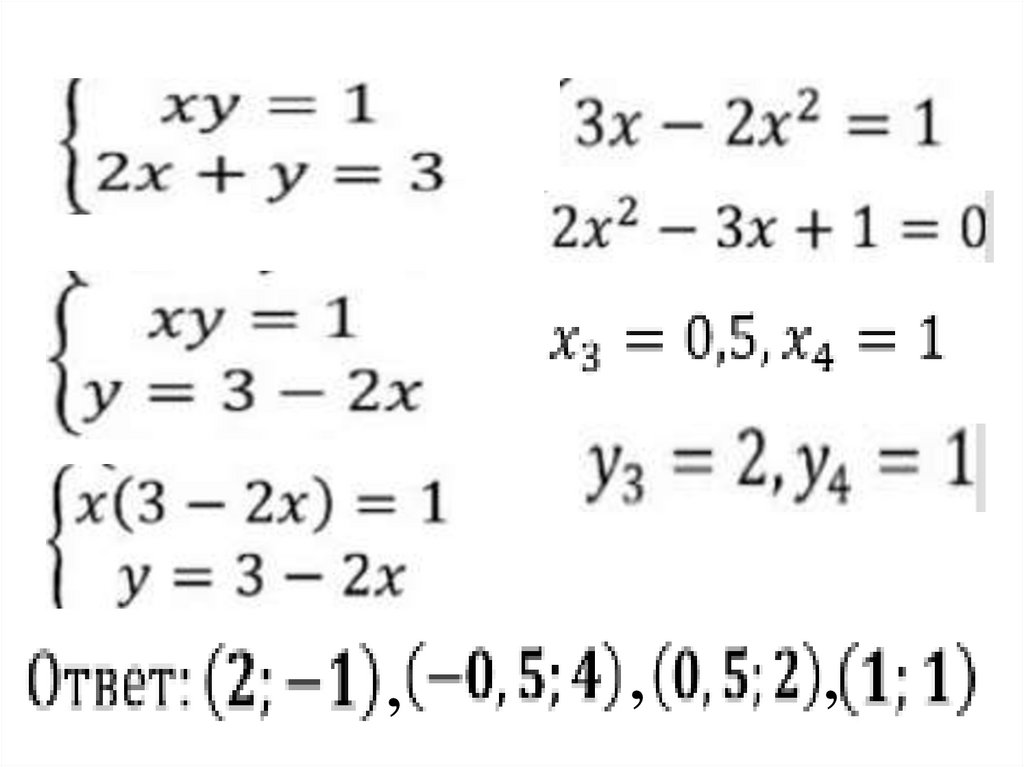

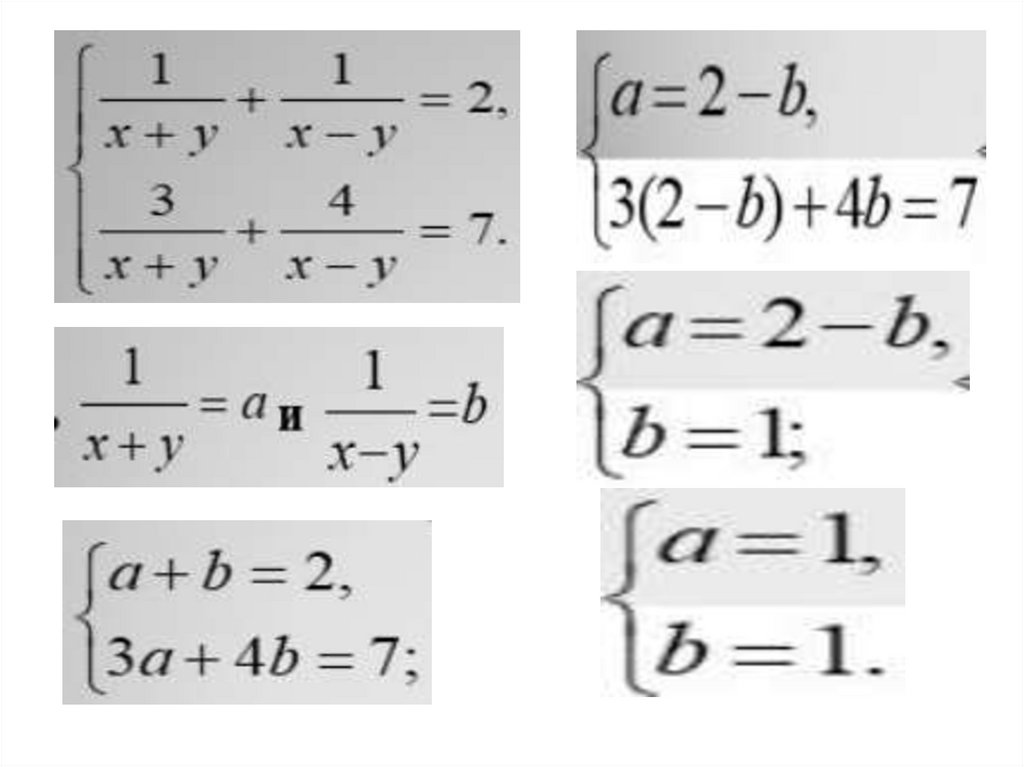


 mathematics
mathematics








