Similar presentations:
Методы и средства защиты компьютерной информации (лекция 1)
1.
Методы и средства защиты компьютернойинформации
2.
Методы и средства защиты информации3.
К. Шеннон «Теория связи в секретных системах»Материал, изложенный в данной статье, первоначально составлял
содержание секретного доклада «Математическая теория криптографии»,
датированного 1 сентября 1945 г., который в настоящее время (1949)
рассекречен.
4.
Имеются три общих типа секретных систем:1) системы маскировки, которые включают применение таких
методов, как невидимые чернила, представление сообщения
в форме безобидного текста или маскировки криптограммы, и
другие методы, при помощи которых
факт наличия сообщения скрывается от противника;
5.
2) тайные системы (например, инвертирование речи),в которых для раскрытия сообщения требуется специальное
оборудование;
6.
3) «собственно» секретные системы,где смысл сообщения скрывается при помощи шифра, кода и т. д.,
но само существование сообщения не скрывается и предполагается,
что противник обладает любым специальным оборудованием,
необходимым для перехвата и записи переданных сигналов.
7.
8.
9.
10.
11.
1212.
13.
14.
15.
Мао В. Современная криптография: теория и практика.:Пер. с англ. –М.:"Вильямс", 2005.-768 с.
16.
Дьяконов В.П. Mathematica 5/6/7. Полное руководство.М.:ДМК Пресс, 2009. -624 с.17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Мао В. Современная криптография: теория и практика.: Пер. с англ.–М.:"Вильямс", 2005.-768 с.
27.
28.
29.
30.
Информация –это некоторые сведения,являющиеся объектом хранения, передачи,
преобразования.
31.
КЛАССИФИКАЦИЯ ЗАЩИЩАЕМОЙИНФОРМАЦИИ И ЕЕ НОСИТЕЛЕЙ
Информацию можно классифицировать по трем основным
признакам:
по принадлежности (праву собственности),
степени секретности,
по содержанию.
32.
Владельцами (собственниками) защищаемой информациимогут быть:
1. Государство и его структуры (органы).
В этом случае к ней относятся сведения, являющиеся
государственной, служебной тайной, иные виды
защищаемой информации, принадлежащей государству
или ведомству.
В их числе могут быть и сведения, являющиеся
коммерческой тайной.
33.
2. Предприятия, товарищества, акционерные общества(в том числе и совместные) и другие —
информация является их собственностью и составляет
коммерческую тайну;
34.
3. Общественные организации —как правило, партийная тайна,
не исключена также государственная и коммерческая тайна;
35.
4. Граждане государства:их права (тайна переписки, телефонных и телеграфных
разговоров, врачебная тайна и др.) гарантируются
государством,
личные тайны — их личное дело.
Следует отметить, что государство не несет ответственность
за сохранность личных тайн.
36.
Всю информацию по степени секретности можно разделитьна пять уровней:
особой важности (особо важная);
совершенно секретная (строго конфиденциальная);
секретная (конфиденциальная);
для служебного пользования (не для печати, рассылается по
списку);
несекретная (открытая).
Чем выше секретность информации определена ее
собственником, тем выше уровень ее защиты, тем более
дорогостоящей она становится, тем уже круг лиц,
знакомящихся с этой информацией.
37.
По содержанию защищаемая информация может бытьразделена на:
политическую,
экономическую,
военную,
разведывательную и контрразведывательную,
научно-техническую,
технологическую,
деловую и коммерческую.
38.
Энтропия и неопределенностьТеория информации определяет количество информации в
сообщении как минимальное число битов, необходимое для
кодирования всех возможных значений сообщения, если
полагать все сообщения равновероятными.
39.
Например, в базе данных для поля дня недели достаточноиспользовать три бита информации, поскольку вся
информация может быть закодирована 3 битами:
000 = Воскресенье
001 = Понедельник
010 = Вторник
011 = Среда
100 = Четверг
101 = Пятница
110 = Суббота
111 ~ Не используется
Если бы эта информация была представлена
соответствующими строками символов ASCII, она заняла бы в
памяти больше места, однако не содержала бы больше
информации.
40.
Аналогично, поле базы данных «ПОЛ» содержит только 1 битинформации, хотя эта информация может храниться и как
одна из двух 7-байтовых строк ASCII:
«МУЖЧИНА» или «ЖЕНЩИНА».
41.
Формально количество информации в сообщении Мизмеряется энтропией сообщения, обозначаемой как Н(М).
В общем случае, энтропия сообщения, измеряемая в битах,
равна log2n, где п - число возможных значений.
При этом предполагается равновероятность всех значений.
42.
В реальном тексте появление букв не равновероятно— одни буквы, как в русском, так и в английском тексте,
встречаются чаще, другие реже.
Частоты, т. е. вероятности появления букв, отражают
структуру языка.
43.
Пусть имеется сообщение, содержащее N последовательныхячеек, - текст из N букв.
В каждой из N ячеек может находиться одна из М букв
( в русском языке М = 32
в английском языке M = 26).
.
В сообщении содержится N 1 букв “а”, N 2 букв “б” и т.д. вплоть
до N 32 букв “я”.
Имеем:
M
N = å Ni
i =1
44.
Вероятность появления данной буквы находим длядостаточно длинного текста, как:
Ni
pi =
N
i=1,2,….M
M
å p(i) = 1
i =1
45.
Общее число различных последовательностей из N буквM-буквенного языка, т. е. число возможных
различных сообщений длиною в N букв, равно:
N!
P=
N1 ! N 2 !...N M !
46.
Количество информации в сообщенииI = log 2 P
ln P
1
N!
I=
=
× ln
ln 2 ln 2
N1 ! N 2 ...N M !
47. Конец лекции 1
воспользовавшись формулойСтирлинга (если N и все Ni велики),
находим:
N ! = ( N / e)
M
1
I»
( N ln N - å N i ln N i ) =
ln 2
i =1
M
1
=N å pi ln pi =
ln 2 i =1
M
= - N å pi log 2 pi
i =1
N
48.
или, в расчете на одну букву,M
I1 = -å pi log 2 pi
i =1
Величина
-å pi log 2 pi
i
была названа Шенноном энтропией.
49.
Количественно энтропия подсчитывается по формуле-k å pi log 2 pi
i
где k — коэффициент, учитывающий выбранное
основание логарифма;
pi — вероятность i-го исхода.
50.
Преимущественно энтропия измеряется в двоичныхединицах (битах), если основанием логарифма выбрано
число 2;
если основание логарифма равно 10, то энтропия
измеряется в десятичных логарифмических единицах
(дитах);
если основанием выбрано число е, то в натуральных
логарифмических единицах (натах).
Благодаря знаку минус, стоящему перед символом
суммирования, энтропия всегда положительна, может
принимать минимальное и максимальное значения,
причем максимальна для ситуации с равновероятными
исходами.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
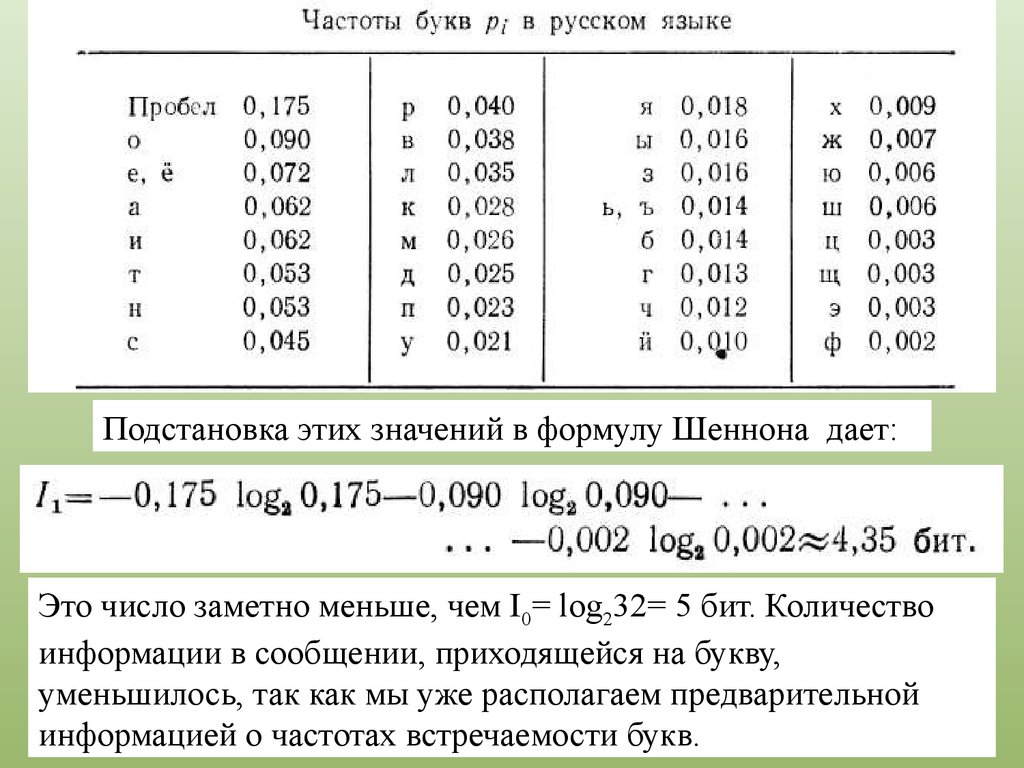
Подстановка этих значений в формулу Шеннона дает:Это число заметно меньше, чем I0= log232= 5 бит. Количество
информации в сообщении, приходящейся на букву,
уменьшилось, так как мы уже располагаем предварительной
информацией о частотах встречаемости букв.
61.
В языке имеются корреляции — определенные частотывстречаемости уже не отдельных букв, а их парных,
тройных, четверных и т. д. сочетаний.
Языковый текст представляет собой сложную цепь
Маркова — вероятность появления данной буквы на
данном месте зависит от того, какие буквы ей
предшествовали.
62.
Математические модели открытого текстаОдин из естественных подходов к моделированию
открытых текстов связан с учетом их частотных
характеристик, приближения для которых можно
вычислить с нужной точностью, исследуя тексты
достаточной длины.
Основанием для такого подхода является устойчивость
частот к -грамм или целых словоформ реальных
языков человеческого общения (то есть отдельных
букв, слогов, слов и некоторых словосочетаний).
63.
Учет частот к -грамм приводит к следующей модели открытоготекста:
Пусть Р(к)(А) представляет собой массив, состоящий из
приближений для вероятностей p(b1b2...bk) появления
к –грамм b1b2...bk в открытом тексте,
А — {a1,...,am} — алфавит открытого текста,
bi Î A,
i = 1,…k.
64.
Источник "открытого текста" генерирует последовательностьc1,с2,...,сk,сk+1 знаков алфавита А,
в которой:
k - грамма c1,с2,...,сk появляется с вероятностью
ÎР
p(c1,с2,...,сk ) e
(к)
(А),
следующая k-грамма с2,...,сk,сk+1 появляется с вероятностью
p(c2...ck+1 )
Р(к)(А) и т. д.
Î
Назовем построенную модель открытого текста
вероятностной моделью к -го приближения.
65.
Таким образом, простейшая модель открытого текста-вероятностная модель первого приближения –
представляет собой последовательность знаков
c1,c2,..., в которой каждый знак
ci , i = 1,2,… появляется
с
вероятностью
ÎP
р(сi )
(1)
(A), независимо от других знаков.
Эта модель также называется позначной моделью открытого
текста.
В такой модели открытый текст с1с2...сl имеет вероятность
l
p (c1c2 ...cl ) = Õ p(ci )
i =1
66.
В вероятностной модели второго приближения первый знак с1имеет вероятность:
р(с1 )
ÎP
(A),
(1)
а каждый следующий знак сi , зависит от предыдущего и
появляется с вероятностью:
p ( ci / ci -1 )
где:
p ( ci -1ci )
=
p ( ci -1 )
p ( ci -1ci ) Î P
( A) ,
( 1)
p ( ci -1 ) Î P ( A )
( 2)
67.
В такой модели открытый текст с1с2…сl имеет вероятностьl
p ( c1c2 ...cl ) = p ( c1 ) × Õ p ( ci / ci -1 )
i =2
68.
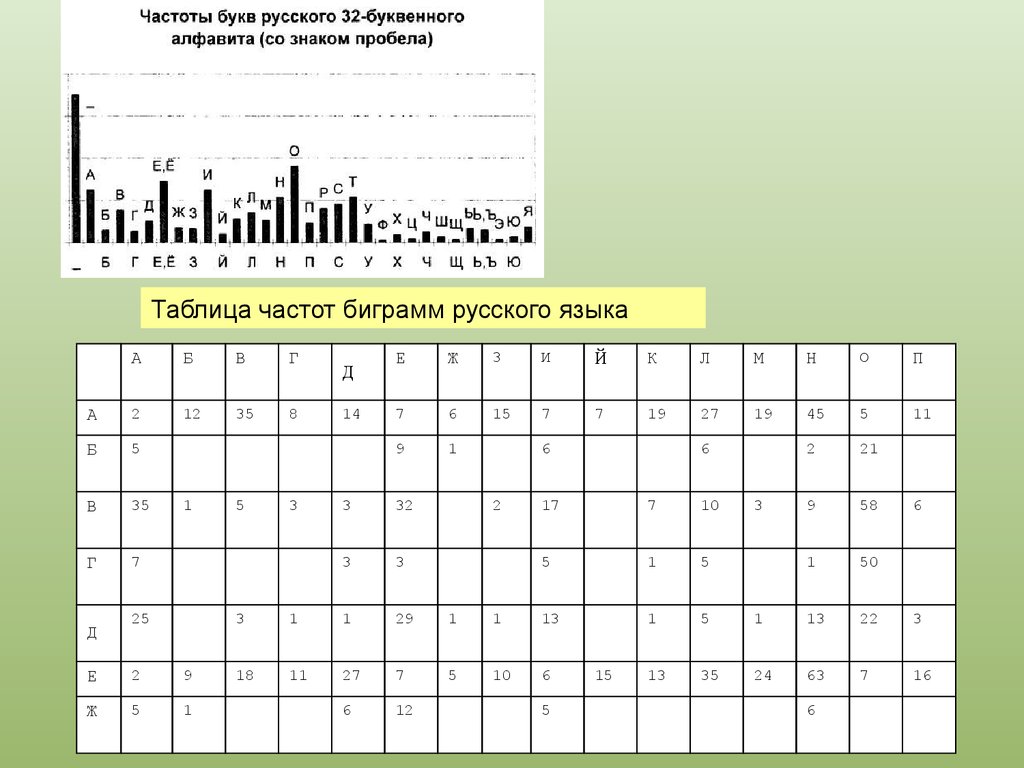
Таблица частот биграмм русского языкаА
Б
В
Г
А
2
12
35
8
Б
5
В
35
Г
7
Д
1
25
Е
2
9
Ж
5
1
5
3
Д
14
Е
Ж
3
И
Й
К
Л
М
Н
О
П
7
6
15
7
7
19
27
19
45
5
11
9
1
2
21
9
58
1
50
3
32
3
3
6
2
6
17
7
10
5
1
5
1
5
1
13
22
3
13
35
24
63
7
16
3
1
1
29
1
1
13
18
11
27
7
5
10
6
6
12
5
15
3
6
6
69.
Модели открытого текста более высоких приближенийучитывают зависимость каждого знака от большего числа
предыдущих знаков.
Чем выше степень приближения, тем более "читаемыми"
являются соответствующие модели.
70.
Проводились эксперименты по моделированию открытыхтекстов с помощью ЭВМ.
1. (Позначная модель) алисъ проситете пригнуть стречи разве
возникл;
2. (Второе приближение) н умере данного отствии официант простояло его то;
3. (Третье приближение) уэт быть как ты хоть а что я
спящихся фигурой куда п;
4. (Четвертое приближение) ество что ты и мы дохнуть
перетусовались ярким сторож;
5. (Пятое приближение) луну него словно него словно из ты
в его не полагаете помощи я д;
6. (Шестое приближение) о разведения которые звенел в
тонкостью огнем только.
Как видим, тексты вполне "читаемы".
71.
Последовательные значения информационной энтропиипри учете все более протяженной корреляции для
русского языка таковы:
Для английского языка Шеннон провел более далекие
оценки:
72.
Язык характеризуется определенной избыточностьюинформации, т. е. возможностью прочитать
осмысленный текст и при нехватке букв.
In стремится к некоторому пределу при возрастании
протяженности корреляций п.
Истинная избыточность есть:
I¥
D¥ = 1 I0
73.
Энтропия языкаДля данного языка энтропия языка равна
H (M )
r=
= -å pi log 2 pi
N
i
Где N - длина сообщения.
74.
Абсолютная энтропия языкаравна максимальному числу битов, которое может быть
передано каждым символом при условии
равновероятности всех последовательностей символов.
Если в языке используются L символов, абсолютная
энтропия равна:
R = log2 L.
Это максимальная энтропия отдельных символов.
Для английского языка с 26 буквами абсолютная
энтропия равна log226, или около 4.7 бит/буква.
75.
Избыточность языка,обозначаемая D определяется как:
D=R-r
Если принять, что энтропия английского языка равна
1.3( для 16-буквенных блоков ), его избыточность
составит 3.4 бит/буква. Это означает, что в каждой
английской букве содержится 3.4 бит избыточной
информации.
76.
Энтропия криптосистемыслужит мерой пространства ключей К.
Энтропия криптосистемы равна логарифму числа
ключей по основанию 2:
77.
Стойкость криптосистемЦель работы криптоаналитика , при расшифровке
некоторого набора символов, заключается в определении
ключа К, открытого текста M, либо их обоих.
Однако он может довольствоваться и некоторой
вероятностной информацией о M:
является ли этот открытый текст оцифрованным звуком,
текстом на каком-либо языке, данными электронных
таблиц, либо чем-то еще.
Цель криптоаналитика - изменение вероятностей,
связанных с каждым возможным открытым текстом. В
конце концов, из груды возможных открытых текстов
будет отобран один конкретный (или, по крайней мере,
весьма вероятный) текст.
78.
Существуют криптосистемы, обеспечивающиесовершенную секретность.
Таковой считается криптосистема, в которой шифртекст
не предоставляет никакой информации об открытом
тексте (кроме, возможно, его длины).
Шеннон теоретически доказал, что такое возможно
только если число возможных ключей столь же велико,
что и число возможных сообщений.
Иными словами, ключ должен быть не короче самого
сообщения и не может использоваться повторно.
79.
Расстояние единственности - U,называемое также точкой единственности, это такой
приблизительный размер шифртекста, для которого сумма
реальной информации (энтропия) в соответствующем открытом
тексте плюс энтропия ключа шифрования равна числу
используемых битов шифртекста
.
Шеннон показал, что шифртексты, которые длиннее расстояния
единственности, можно дешифровать только одним
осмысленным способом.
Шифртексты, которые заметно короче расстояния
единственности, вероятнее всего, можно дешифровать
несколькими способами, причем каждый из них может быть
корректен, и таким образом обеспечить защиту сообщения,
поставив противника перед выбором правильного открытого
текста.
80.
В большинстве симметричных криптосистем расстояниеединственности определяется как частное от деления
энтропии криптосистемы на избыточность языка.
Расстояние единственности не позволяет сделать точное
предсказание, но дает вероятностный результат. Оно
позволяет оценить минимальный объем шифртекста,
при лобовом вскрытии которого имеется, вероятно,
только один разумный способ дешифрования.
81.
Расстояние единственности служит мерой не объемашифртекста, необходимого для криптоанализа, а объема
шифртекста, необходимого для достижения единственности
результата криптоанализа.
Криптосистема может быть неуязвима к вскрытию
вычислительными методами, хотя, теоретически, её можно
взломать- если используется небольшой объем шифртекста.
Расстояние единственности обратно пропорционально
избыточности. Если избыточность стремится к нулю, даже
заурядный шифр может не поддаться вскрытию с
использованием только шифртекста.
82.
Шеннон определил криптосистему с бесконечнымрасстоянием единственности, как идеально секретную.
Идеально секретная криптосистема не обязательно
совершенна, но совершенная криптосистема обязательно
идеальна.
Если криптосистема идеально секретная, то даже после
успешного криптоанализа остается некоторая
неопределенность в правильности восстановленного
открытого текста.















































































 informatics
informatics








