Similar presentations:
Умножение смешанных чисел
1. Умножение дробей. Свойства умножения.
2.
Проверка домашнегозадания:
№334, 336,
340(1,2)
3.
Умножение
4.
Расшифруйте ребус:Свойства
5.
Умножение.10.11.20г
Свойства умножения
6.
Умножение чисел и егосвойства
1. Переместительное свойство умножения:
а∙b=b∙a
2. Сочетательное свойство умножения:
а ∙ (b ∙ с) = (a ∙ b) ∙ с
3. Распределительное свойство умножения
относительно
сложения:
а ∙ (b + c ) = а·b + a·c
относительно
вычитания:
а ∙ (b - c ) = а·b - a·c
7.
НА НАТУРАЛЬНОЕ ЧИСЛО4 • 7 = 4 • 7 = 28 = 5 3
5
5
5
5
ПРАВИЛО: чтобы умножить дробь на натуральное
число, надо её числитель умножить на это число, а
знаменатель оставить без изменения.
8.
НА ДРОБЬ4 • 3 = 4 • 3 = 12
77
7 11 7 • 11
ПРАВИЛО: чтобы умножить дробь на дробь, надо:
1) найти произведение числителей и произведение
знаменателей этих дробей;
2) первое произведение записать числителем, а
второе – знаменателем.
9.
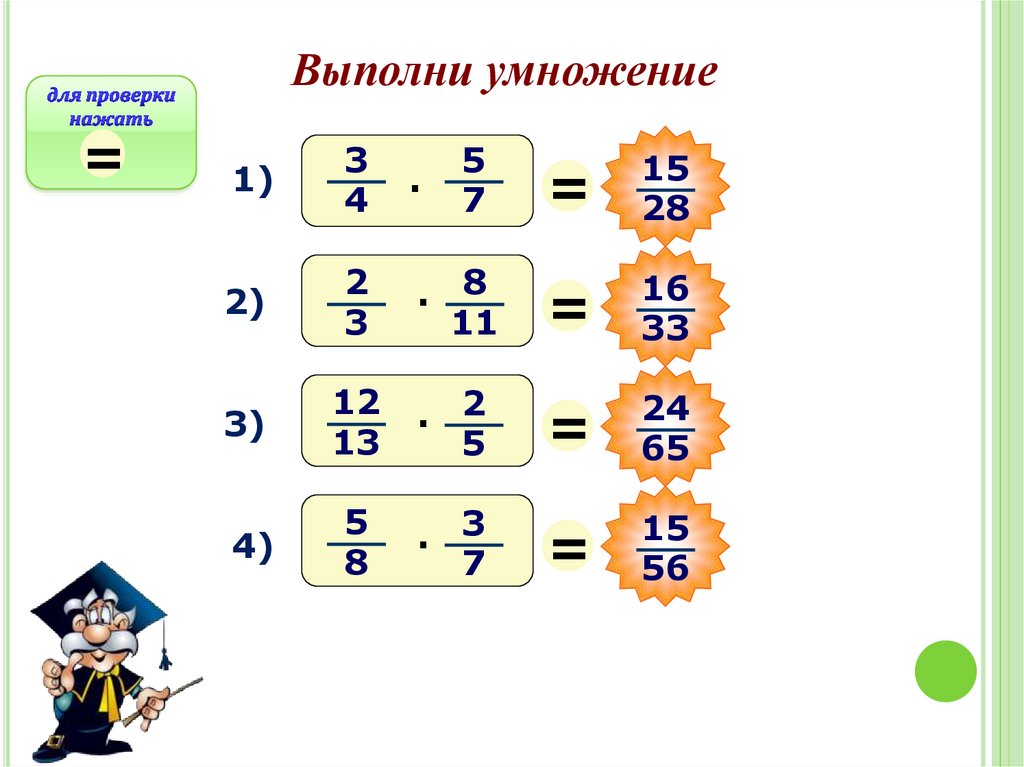
Выполни умножение=
1)
3
4
2)
2
3
3)
12
13
4)
5
8
·
5
7
·
8
11
·
2
5
·
3
7
=
15
28
=
16
33
=
24
65
=
15
56
10.
12
15 3 3
1
3
12 2 4
=
6 • 11
5
3
=
3 • 11
2
4
=
22
5
=
4
2
5
=
33
8
=
4
1
8
11.
Действуем по алгоритму6
4
=24
1
1
1. превратить их в неправильные дроби;
2. умножить по правилу умножения
обыкновенных дробей;
3. если необходимо, сократить полученную
дробь и выделить целую часть.
12.
Физминутка13.
14.
Работа по учебнику:Стр. 70, №337,
№339 (3,4).
15.
Найдите значение выражения,используя распределительное
свойство умножения
а ∙ (b + c ) = а·b + a·c
Пример №1:
3
1
2
1
16.
Найдите значение выражения,используя распределительное
свойство умножения
а·b + a·c = а ∙ (b + c )
Пример №2:
1
4
17.
Работа по учебнику:Стр. 70,
№341 (1,2,3,6,7,8).
18.
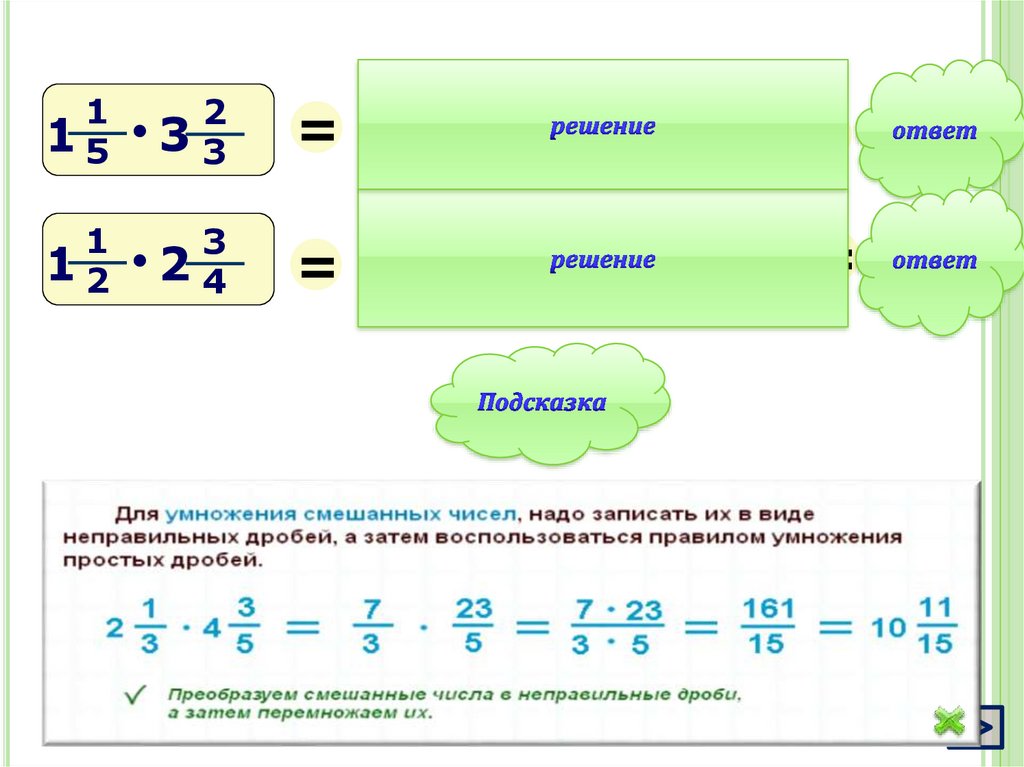
Чтобы перемножить смешанные числа,надо:
1. превратить их в неправильные
дроби;
2. умножить по правилу
умножения обыкновенных дробей;
3. если необходимо, сократить
полученную дробь и выделить
целую часть.
19.
20.
Домашнее задание§11(вопр. 1-4),
№ 338,
№ 342,
№ 340 (3,4).


















 mathematics
mathematics








