Similar presentations:
Основные положения булевой алгебры
1.
§2. ОСНОВНЫЕ ПОЛОЖЕНИЯБУЛЕВОЙ АЛГЕБРЫ
2.
2.1. БУЛЕВА АЛГЕБРА И ЕЕ ПРИМЕНЕНИЕ2.1.1. Определение булевой алгебры
3.
Название этого раздела математики связанос именем его основателя – Джорджа Буля.
БУЛЬ (Boole) Джон английский математик
и логик, один из основоположников
математической
логики.
Разработал
алгебру
логики
(булеву
алгебру)
(«Исследование законов мышления»,
1854),
основу
функционирования
цифровых компьютеров.
4.
Используя классическое понятие алгебры,булеву алгебру можно определить как систему
А=(В,φ1,φ2,…, φn), в которой несущим множеством
является двухэлементное множество двоичных
чисел В={0,1}, а Ώ={φ1,φ2,…, φn} – заданные на этом
множестве логические операции, сущность которых
рассмотрим позднее.
5.
Основныелогические
операции,
дизъюнкция, конъюнкция и отрицание, - можно
интерпретировать как операции, введенные в
теории множеств: свойства указанных операций
аналогичны свойствам операций объединения,
пересечения
и
дополнения
множеств
соответственно.
Однако
логические
операции
имеют
несколько
иной
смысл;
они
позволяют
формировать простые и сложные высказывания.
Все
множество
логических
операций
обозначается Е2.
6.
Как правило, существует логическаяинтерпретация элементов множества В:
1 – истинно; 0 – ложно.
В ряде случаев такой смысл не
придается, и в качестве элемента множества
рассматривается двоичная переменная (ее
называют
также логическая или булева
переменная) x, которая принимает значения
x = 0 или x = 1.
7.
2.1.2. Области применения булевой алгебры8.
Булева алгебра применяется:1) как средство алгоритмического описания в
языках
программирования
для
определения
логических условий;
2) как средство формирования логических
высказываний
в
математической
логике,
лингвистике, теории искусственного интеллекта;
3) как средство разработки
дискретных технических систем;
и
описания
4) как формальная модель лежащая в основе
языков программирования.
9.
Алгебра логики позволяет производитьанализ и синтез логических устройств.
Анализ
–
это
поиск
аналитического
выражения, которое описывает работу системы.
Синтез
– обратная задача:
создание
технического
устройства
на
основе
математического описания средствами булевой
алгебры.
10.
2.1.3. Высказывания11.
Одним из базовых понятий в булевой алгебреявляется понятие высказывания.
Высказывание
–
это
любое
повествовательное предложение, в отношении
которого имеет смысл утверждение о его
истинности или ложности.
Обычно
высказывания
обозначаются
буквами латинского алфавита: a , b, c, A, B , C .
Для
каждого
высказывания
вводится
значение истинности, которое может принимать
одно из двух возможных: значений 1 – истина, 0 –
ложь.
12.
Пример.утверждений:
Рассмотрим
справедливость
а) число 4 – четное;
b) снег – красный;
с) 2*2=5.
Значения истинности данных высказываний
следующие: a=1, b=0, c=0.
13.
Два высказывания A и B называютсяэквивалентными, если их значения истинности
совпадают.
Значение
истинности
может
быть
постоянным либо изменяется в зависимости от
обстоятельств.
Изменяемое
высказывание
может
рассматриваться как переменный параметр –
двоичная переменная, принимающая одно из двух
значений (обозначается x, y, z).
14.
2.2. ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ15.
2.2.1. Понятие функции и способы ее задания16.
Пусть имеется n двоичных переменныхx1, x2, …, xn. Каждая из них в
случае может принимать
Полученный
набор
двоичный вектор длины n.
набору можно поставить в
значений 0 или 1.
некотором конкретном
значение 0 или 1.
элементов
есть
Каждому конкретному
соответствии одно из
17.
Функцияf,
задающая
однозначное
отображение множества всевозможных наборов
значений двоичных переменных x1, x2, …, xn во
множество {0,1}
называется функцией алгебры
логики (или логической функцией, булевой
функцией, переключательной функцией):
f x1 , x2 , ..., xn y; y 0 или y 1
Таким образом, логическая функция – это
зависимость, которая устанавливает связь между
сочетанием
значений
входных
двоичных
переменных и двоичным значением этой функции.
18.
Способы задания функции.функция может быть задана:
Логическая
1) математическим выражением (формулой);
2) таблицей.
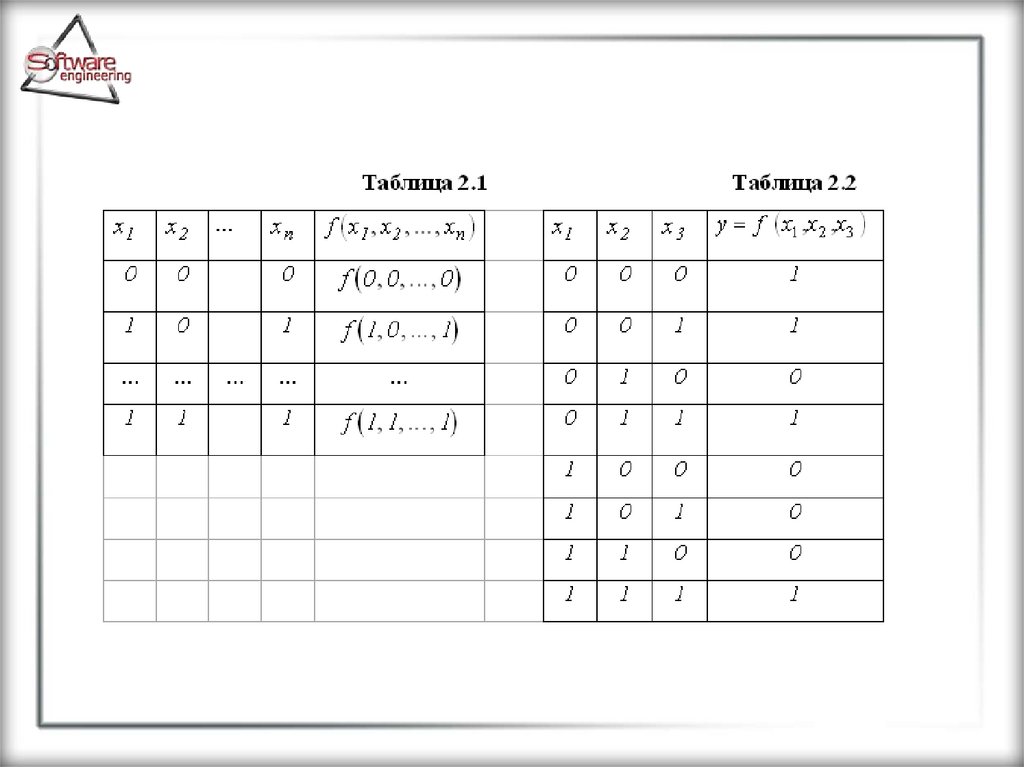
Таблица является наиболее общим и
универсальным способом задания функции. В её
левой части перечисляют всевозможные наборы
значений двоичных переменных, а в правой —
значения функции на этих наборах.
Такие таблицы, описывающие функции,
называют таблицами истинности. В таблицах 2.1 и
2.2 приведены примеры таблиц истинности.
19.
20.
Оценим число возможных наборов (числострок входных переменных).
Конкретный набор – это вектор значений
b1 ,b2 ,...,bn
Количество наборов – это мощность прямого
произведения n двухэлементных множеств B:
n
a B B 2n
n
где n– число входных элементов.
21.
Оценим возможное количество вариантовлогических функций от n переменных. Множество
вариантов логической функции можно представить
как прямое произведение:
M B1 B2 ... Bi ... Ba B
a
где Bi – значение функции на наборе i.
Таким образом, общее количество функций от
n переменных
a
m B B 2a
a
где a 2 n .
22.
Наборы, на которых функция равна единице,называют единичными наборами, а наборы, на которых
функция равна нулю, называют нулевыми.
Если функция при любых значениях аргументов
принимает значение 0, то такую функцию называют
нулевой или константой 0 (тождественно ложная
функция).
Функция, которая на всех наборах равна 1, называется
единичной или константой 1 (тождественно истинная
функция).
Если функция определена не на всех наборах
аргументов, то она называется не полностью
определенной или частично определенной.
23.
Две булевы функцииf x1 , x2 , ..., xn и x1 , x2 , ..., xn называют равными,
если для всех возможных наборов значений
аргументов они принимают одинаковые значения и
таким образом имеют одну и ту же таблицу
истинности, и записывают:
f x1 , x2 , ..., xn x1 , x2 , ..., xn
24.
Говорят, что булева функцияСущественно зависит от аргумента
f x1 , x2 , ..., xn
xi , если
f x1 , x2 , ..., xi 1 , 0 , xi 1 , ..., xn f x1 , x2 , ..., xi 1 , 1, xi 1 , ..., xn ,
хотя бы для одного набора остальных аргументов.
В противном случае xi называется несущественной
или фиктивной переменной (ее можно исключить).
25.
2.2.2. Элементарные логические операции26.
Измножества
логических
функций
выделяется ряд наиболее простых операций,
которые имеют ясную логическую интерпретацию:
1) отрицание (инверсия)
f 1 x x
Отрицание – это функция,
выражающая
высказывание,
которое
истинно,
если
высказывание ложно, и ложно,
если истинно.
(читается: не).
27.
2) дизъюнкция (логическое сложение)f 2 x, y x y
(читается: " x или y ").
Дизъюнкция
–
это
функция,
выражающая
высказывание,
которое
истинно тогда и только
тогда, когда, по крайней
мере,
одно
из
высказываний x или y
является истинным.
28.
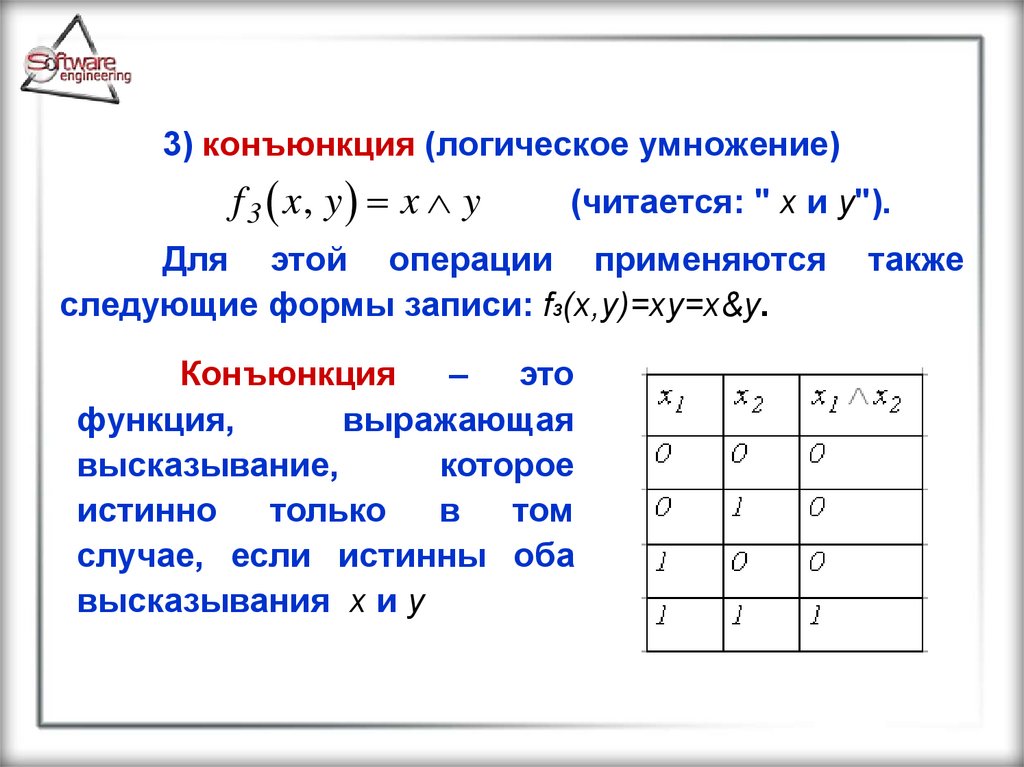
3) конъюнкция (логическое умножение)f 3 x, y x y
(читается: " x и y").
Для этой операции применяются
следующие формы записи: f3(x,y)=xy=x&y.
Конъюнкция
– это
функция,
выражающая
высказывание,
которое
истинно
только
в
том
случае, если истинны оба
высказывания x и y
также
29.
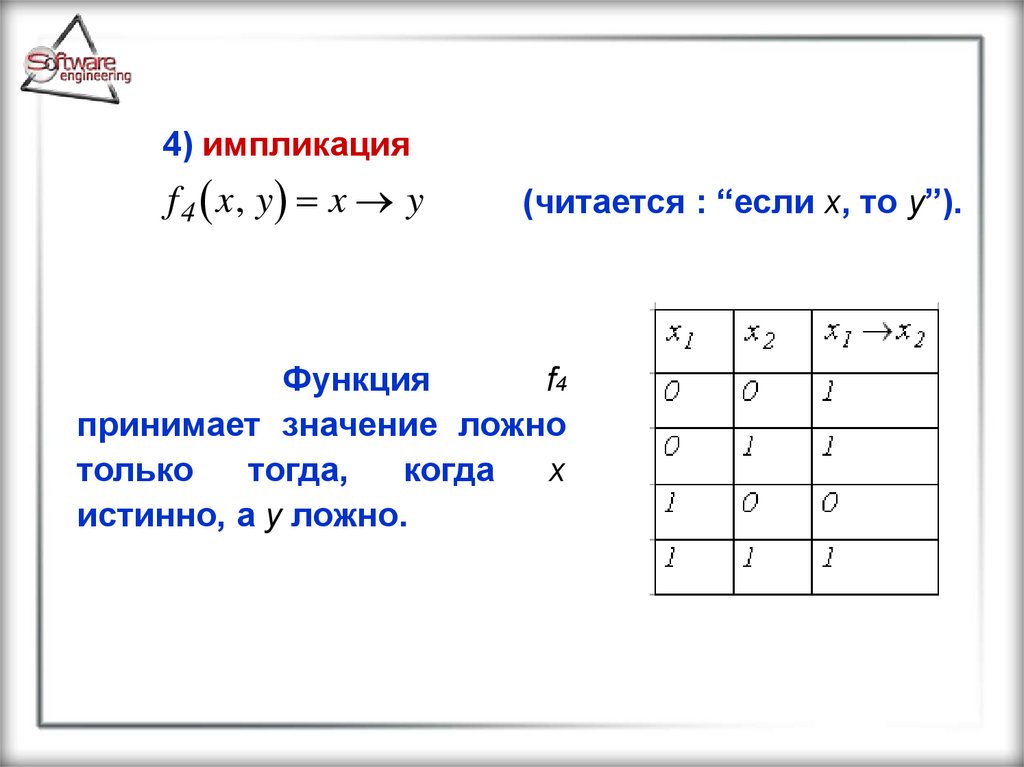
4) импликацияf 4 x, y x y
(читается : “если x, то y”).
Функция
f4
принимает значение ложно
только
тогда,
когда
x
истинно, а y ложно.
30.
5) эквивалентность (равнозначность)f 5 x, y x ~ y
(читается:
Функция f5=1 тогда и
только тогда, когда значения
обоих аргументов x и y
совпадают
“x равно y ”).
31.
6)сложение
(неравнозначность)
по
f 6 x, y x y
Функция f6 истинна
тогда и только тогда, когда
значения
аргументов
различны,
функция
является обратной к f5
модулю
два
32.
7) штрих Шеффераf7 x , y x y
Операция обратная по
отношению к конъюнкции
(функция
ложна,
только
если
оба
аргумента
истинны)
33.
8) стрелка Пирсаf 8 x, y x y
Функция f8 обратная к
дизъюнкции
(f8
истинно,
только когда x и y ложны)
34.
Наиболее важными функциями являютсяпервые три. Остальные могут быть выражены
через эти три функции. С использованием трех
основных функций (дизъюнкции, конъюнкции и
отрицания) могут образовываться более сложные
функции.
Поэтому можно
дать
еще одно
определение булевой алгебры.
Булевой алгеброй называется алгебра типа,
B, , ,
несущим множеством которой является
множество двоичных чисел, а операциями конъюнкция, дизъюнкция и отрицание.































 mathematics
mathematics








