Эмпирические законы кристаллографии

1.

Эмпирические законы
кристаллографии
1) Формула Эйлера-Декарта
Рене Декарт
1596 - 1650
Леонард Эйлер
1707 - 1783
1

2.

2) Закон Браве
Огюст Браве
1811 - 1863
• Морфологическая значимость грани, то есть ее
относительное развитие на кристалле, пропорциональна
ее ретикулярной плотности.
То есть, кристалл при
росте покрывается гранями с наибольшей ретикулярной
плотностью.
• Спайность кристалла (способность скалываться по
определенным плоскостям под действием удара или
давления), как правило, происходит по плоскостям с
наибольшей ретикулярной плоскостью.
2

3.

3) Закон Стено (Стенона) - Роме де Лиля :
Кристаллы разной формы одного вещества имеют неизменные
углы между соответственными гранями.
Или
Изменение относительных размеров и формы граней, их
расстояний от центра кристалла, то есть линейных параметров
кристалла, оставляет неизменными его угловые параметры,
которые являются устойчивыми характеристиками формы
кристалла, а значит, и его симметрии.
Прибор для измерения
двугранных углов –
гониометр
Нильс Стенсен
Николай Стенон
Николас Стено
1638 - 1686
3

4.

3) Закон постоянства симметрии: все кристаллы определенного вещества, вне
зависимости от их формы, имеют одинаковую симметрию.
4

5.

4) Закон Гаюи
Рене Жюст Гаюи
1743 – 1822 гг.
Отношения параметров, отсекаемых двумя
любыми гранями кристалла на трех
пересекающихся ребрах, равны отношениям целых
и сравнительно малых чисел (почему?)
5

6.

5) Закон Вейса – закон зон
Установлена связь между
символами граней и символами
ограничивающих их ребер
Христиан
Самюэль
Вейс
1780-1856
6

7.

h, k, l R
Поскольку ребро с символами [rst] (hkl),
r,s,t – координаты точки на ребре, то получаем:
7

8.

Поиск ребра, общего для двух
пересекающихся граней
Поиск плоскости, общей для двух
пересекающихся ребер
Метод перекрестного умножения
8

9.

Следствия закона Вейса (закона зон)
9

10.

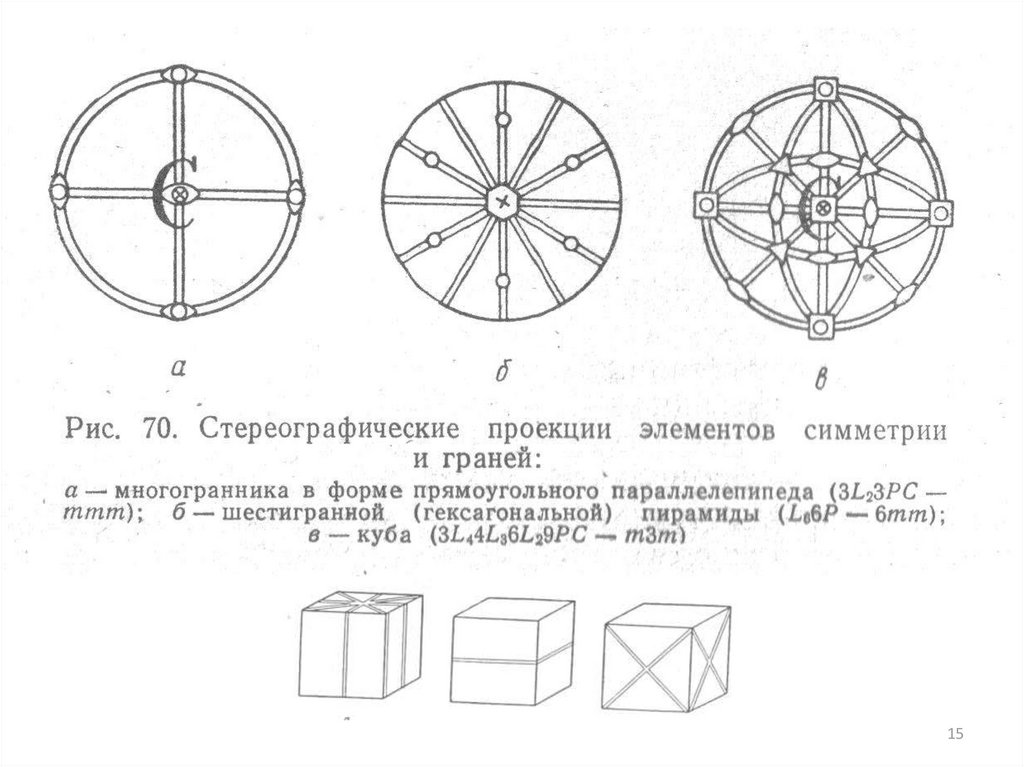
Стереографические проекции
Проекции граней кристалла
Горизонтальные грани проецируются в центре круга проекций,
Вертикальные – на самом круге проекций,
Наклонные – внутри круга проекций.
10

11.

Сферические координаты грани А
- широта – угол между вертикальной осью III и направлением,
- долгота – угол между осью II и направлением.
Стереографическая проекция перпендикуляра к грани
называется гномостереографической проекцией грани.
11

12.

12

13.

Сетка Вульфа
Плоскость проекций –
экваториальная плоскость
13

14.

Проецирование элементов симметрии
Стереографические проекции осей симметрии: а – вертикальная ось, б –
горизонтальная ось (Y),
в – 4L3 ориентированы косо относительно плоскости проекций.
Стереографические проекции плоскостей симметрии: а – вертикальная плоскость
(параллельна оси I), б – горизонтальная плоскость,
в – ориентирована косо относительно плоскости проекций
14

15.

15

16.

16

17.

Метод косинусов Вульфа
Нормаль N0 образует с
17

18.

Теоремы сложения
(взаимодействие элементов симметрии)
Теорема 1:
4
1
2
3
Линия пересечения двух плоскостей
симметрии является осью симметрии,
действие
которой
равно
сумме
действий
обеих
плоскостей;
элементарный угол поворота оси вдвое
больше
угла,
образованного
плоскостями.
Обратная теорема:
Действие одной поворотной оси равносильно действию двух зеркальных плоскостей,
пересекающихся вдоль нее. При этом первая плоскость проводится вдоль оси
произвольно, а вторая должна образовать в направлении поворота оси с первой
плоскостью угол, равный половине элементарного угла поворотной оси.
18

19.

Теорема 2 (Теорема Эйлера). Поворот вокруг двух
пересекающихся осей симметрии эквивалентен повороту
вокруг третьей оси, им равнодействующей (и проходящей
через точку их пересечения).
Найти положение равнодействующей оси и ее элементарный угол
поворота можно следующим образом:
1) через исходные оси проводим плоскость 1;
2) через одну из осей проводим плоскость 2 под углом к плоскости 1,
равным половине элементарного угла поворота этой оси;
3) через вторую ось проводим плоскость 3 под углом к плоскости 1,
равным половине элементарного угла поворота этой оси;
4) линия пересечения плоскостей 2 и 3 будет искомой равнодействующей
осью симметрии, а угол между плоскостями 2 и 3 равен половине
элементарного угла поворота этой оси;
Если исходные оси симметрии однородные (обе простые или обе
инверсионные), равнодействующая ось будет простой; если же они
разнородные (одна простая, другая инверсионная), то равнодействующая
ось будет инверсионной.
19

20.

Ln1 ( 1= 360/n1)
Ln2 ( 2= 360/n2)
2/2
1/2
1
/2
3
Ln ( = 360/n)
2
20

21.

Теорема 3.1.
При наличии центра инверсии С и четной оси L2n
перпендикулярно последней проходит плоскость
симметрии Р.
Теорема 3.2.
При наличии центра инверсии С и проходящей через него
плоскости симметрии Р перпендикулярно последней
находится четная ось симметрии L2n.
Теорема 3.3.
При наличии четной оси L2n и перпендикулярной к ней
плоскости симметрии Р всегда присутствует центр
инверсии С.
PC=L2n,
L2nP=C
L2nС= P
Следствие: При наличии центра инверсии сумма четных осей
равна сумме плоскостей симметрии, причем каждая четная
ось перпендикулярна плоскости симметрии.
21

22.

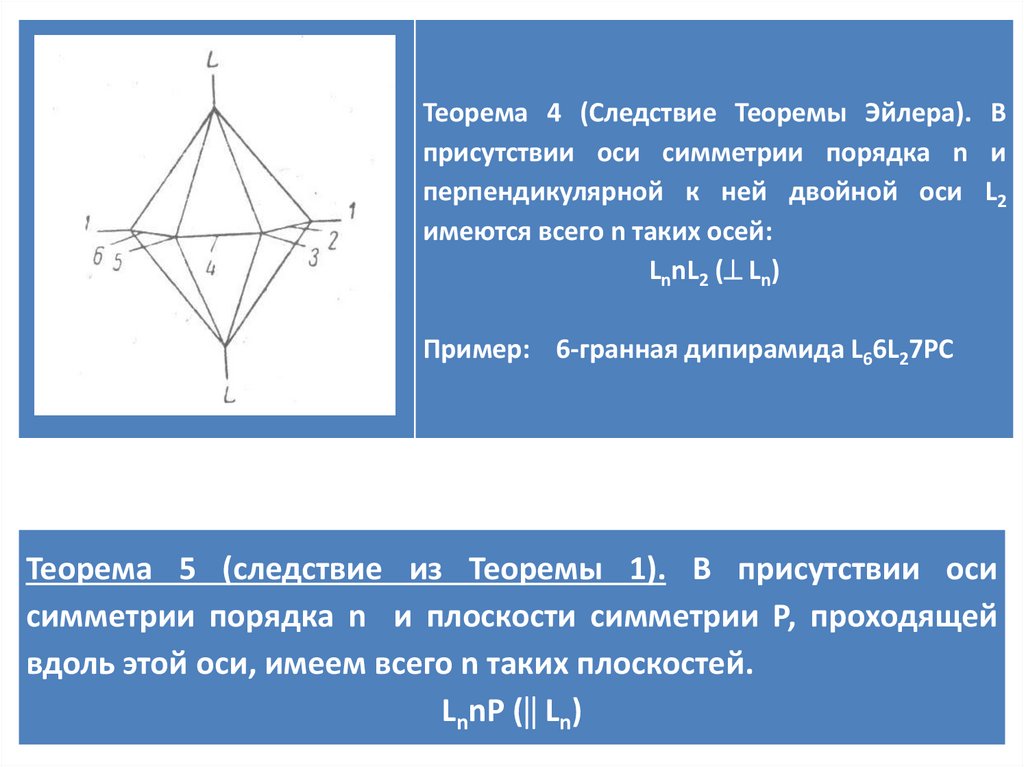
Теорема 4 (Следствие Теоремы Эйлера). В
присутствии оси симметрии порядка n и
перпендикулярной к ней двойной оси L2
имеются всего n таких осей:
LnnL2 ( Ln)
Пример: 6-гранная дипирамида L66L27PC
Теорема 5 (следствие из Теоремы 1). В присутствии оси
симметрии порядка n и плоскости симметрии Р, проходящей
вдоль этой оси, имеем всего n таких плоскостей.
LnnP ( Ln)
22

23.

Виды симметрии
№
Название
Описание
Обозначение
1
Примитивные
одна поворотная ось симметрии порядка n
Ln
2
Инверсионнопримитивные
одна инверсионная ось симметрии порядка n
Lin
3
Центральные
поворотная ось симметрии порядка n и центр инверсии
Ln C
4
Планальные
поворотная ось симметрии порядка n и проходящая LnnP (//)
через нее плоскость симметрии
5
Инверсионнопланальные
инверсионная ось симметрии порядка n и проходящая LinnP (//)
через нее плоскость симметрии
6
Аксиальные
7
Аксиальноцентральные
поворотная
ось
симметрии
порядка
n
и LnnL2 ( )
перпендикулярная ей поворотная ось симметрии второго
порядка
набор элементов симметрии аксиального семейства и LnnL2 ( ) C
центр инверсии
(Планаксиальные)
23

24.

Синогния
Триклинная
Моноклинная
Параметры ЭЯ
a b c
Особенности
симметрии
нет симметрии
90
или только C
a b c
L2 и/или P
Разнообразная, часто
длинные призмы
3L2 (взаимно
перпенд.)
Призмы, вискеры
= = 90 , 90
Ромбическая
(Орто-ромбическая)
Тригональная
(Ромбоэдрическая)
Тетрагональная
a b c
= = = 90
a = b =c
и/или 3P (тоже
взаимно перп.)
L3 или Li3
Примеры
Разнообразный
Плагиоклаз,
аксинит
Пироксены,
амфиболы,
ортоклазы
Оливин,
андалузит, барит
Ромбоэдры,
тригональные призмы
Кальцит,
доломит, кварц, турмалин
L4 или Li4
Короткие призмы
Циркон,
касситерит
L6 или Li6
Гексагональные
призмы и пирамиды
Апатит, берилл,
-кварц
4L3
Изометрические
кристаллы
Галит, магнетит,
гранат
= = < 120 90
a=b c
Габитус
= = = 90
Гексагональная
a=b c
= = 90 ,
= 120
Кубическая
a = b =c
= = = 90
24

25.

Ln
Ln C Ln nP (//) L nL ( ) L nL ( )C
n 2
n 2
Lin
Lin nP (//)
25

26.

Направления в кристалле, связанные элементами
симметрии, называются симметрично-равными.
Направления, которые не размножаются элементами
симметрии (им нет эквивалентных, симметричноравных) называются единичными.
Чем выше симметрия кристалла, тем меньше в нем
единичных направлений
Категория
Высшая
Единичных
направлений
0
Средняя
1 (совпадает с Ln, n>2)
Низшая
>1
Почему важно?
Свойства!
26

27.

Полярными являются направления, противоположные концы которых
не могут быть совмещены элементами симметрии кристалла.
С этими направлениями связаны свойства пироэлектриков –
диэлектрики, обладающие спонтанной электрической поляризацией Р.
-
Пьезоэлектрики - Р под действием давления или деформации;
Сегнетоэлектрики - Р под действием вн. поля Е.
Р = Z + E
, Z – напряжение, Е – эл. поле.
Полная свободная
энергия системы с
N=const
F = PV – TS – HM – EP
27

28.

Применение: сенсоры, детекторы и приемники излучений, датчиков тепла.
Любой вид радиации, попадающий на пироэлектрический образец,
вызывает изменение его температуры и соответствующее изменение
28
поляризации.

29.

Символы Шёнфлиса
Сn — единственное особое направление (Ln)
Cnv (от нем. Vertical) — с nP( )
Cnh (от нем. Horisontal) — P( ).
S2n (от нем. Spiegel — зеркало) — единственная Li2n (Sn = Cnh).
Сni — единственная Lin.
Dn — Сn + nL2 ( ).
Dnh — +P ( ) + nP .
Dnd (от нем. Diagonal — диагональный) — nP ( ) по диагонали
между горизонтальными осями L2.
Tn , On, In (Yn) — высшая категория, совокупность осей в
Тетраэдре, Октаэдре или кубе, Икосаэдре или Додекаэдре.
29

30.

Международные символы точечных групп
Предложены немецким кристаллографом Карлом
Германом в 1928 году и модифицированые французским
минералогом Шарлем-Виктором Могеном в 1931 году.
1, 2, 3, 4, 6 – поворотные оси
m–
плоскость симметрии
_ _ _ _ _
1, 2, 3, 4, 6 - инверсионные оси.
Ориентация элемента относительно координатных осей
задаётся позицией элемента в символе группы.
Если ось симметрии перпендикулярна плоскости, то они
записываются в виде дроби.
30

31.

НИЗШАЯ КАТЕГОРИЯ
Если в символе группы 3 позиции, то первая отвечает направлению вдоль
оси X, вторая – вдоль оси Y, третья – вдоль оси Z. Сюда относятся 8 групп:
1
-1
2
m
2/m
222
mm2
2/m2/m2/m
СРЕДНЯЯ КАТЕГОРИЯ
1 - направление главной оси Z,
2 — побочное направление X и Y,
3— диагональное направление между X и Y.
Сюда относятся 19 групп:
ВЫСШАЯ КАТЕГОРИЯ
1 — эквивалентные направления X, Y, Z,
2 — всегда присутствующие там четыре оси 3 или -3,
3 — диагональное направление между координатными осями.
Сюда относятся только 5 групп :
и -43m
31