Similar presentations:
Параллельные прямые
1.
2.
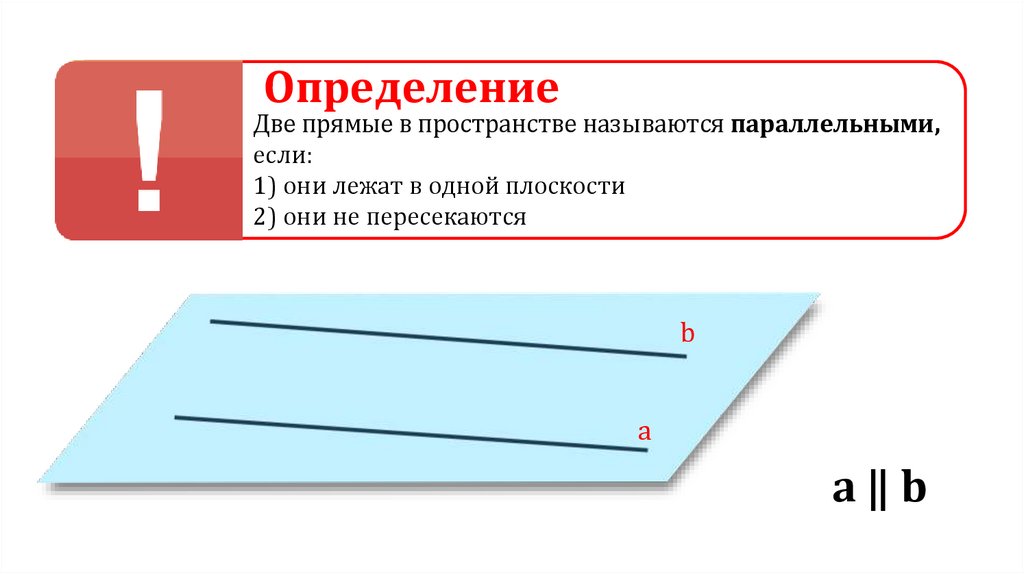
ОпределениеДве прямые в пространстве называются параллельными,
если:
1) они лежат в одной плоскости
2) они не пересекаются
b
a
a‖b
3.
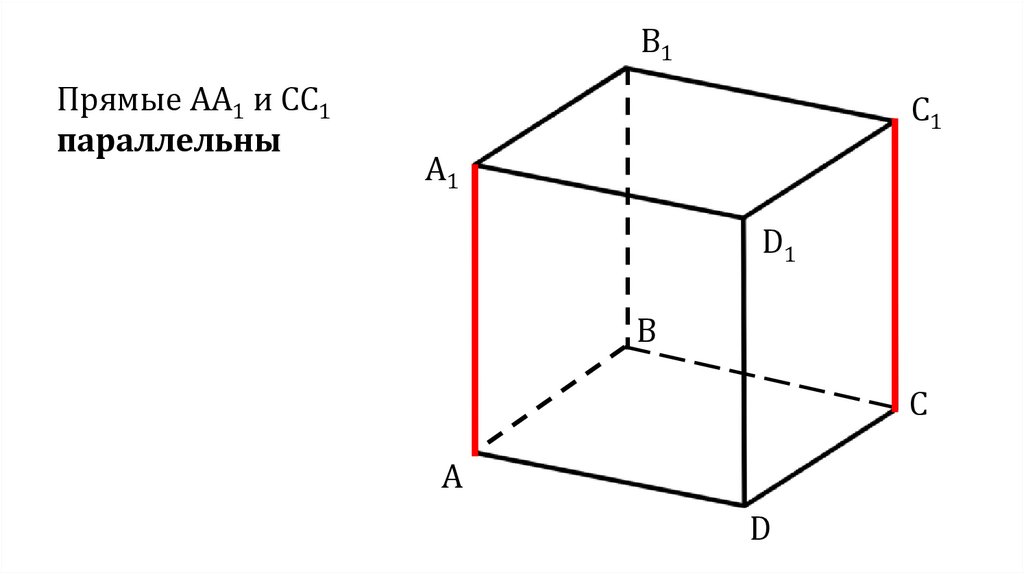
B1Прямые АА1 и СС1
параллельны
C1
A1
D1
B
C
A
D
4.
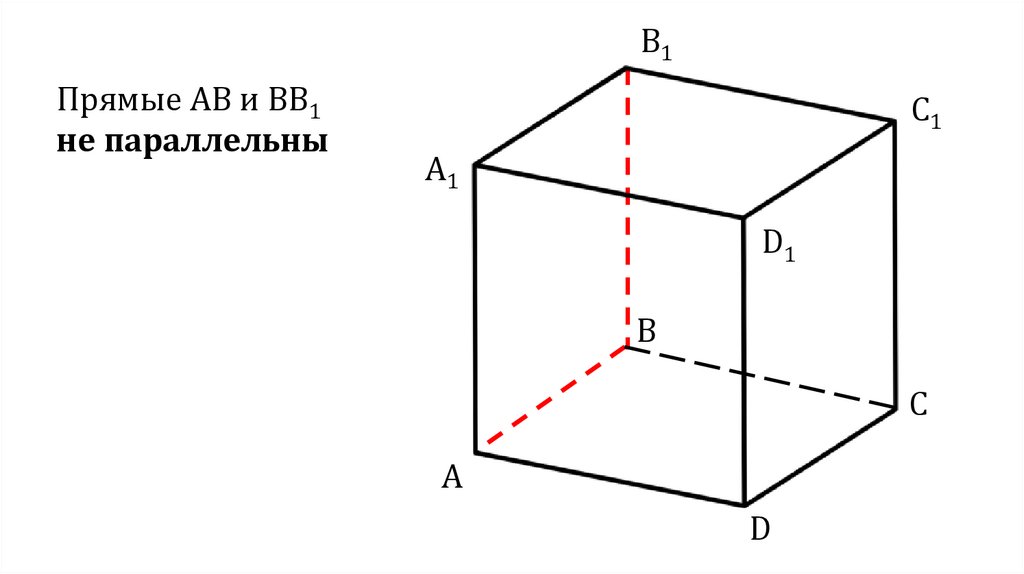
B1Прямые АВ и ВВ1
не параллельны
C1
A1
D1
B
C
A
D
5.
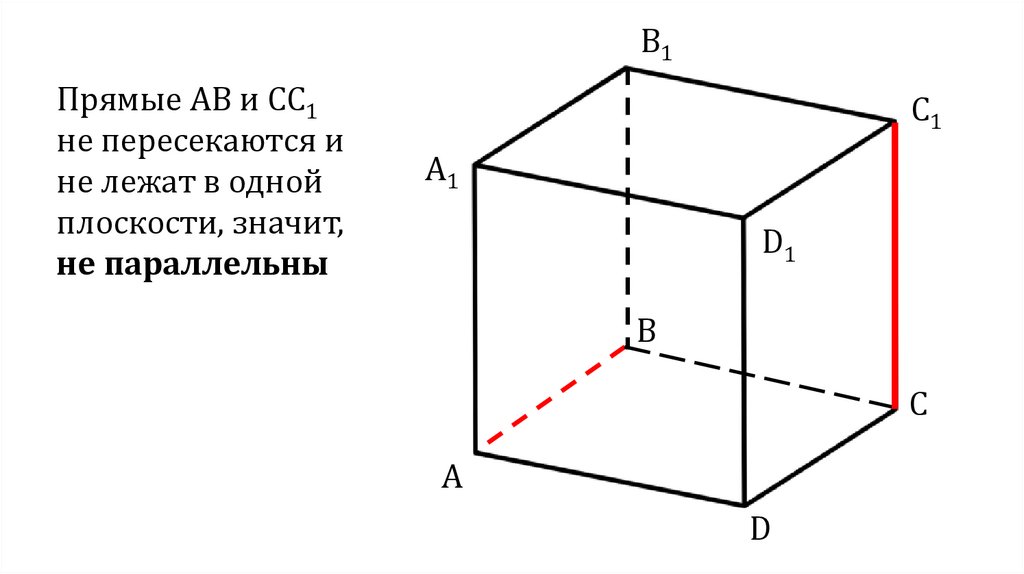
B1Прямые АВ и СС1
не пересекаются и
не лежат в одной
плоскости, значит,
не параллельны
C1
A1
D1
B
C
A
D
6.
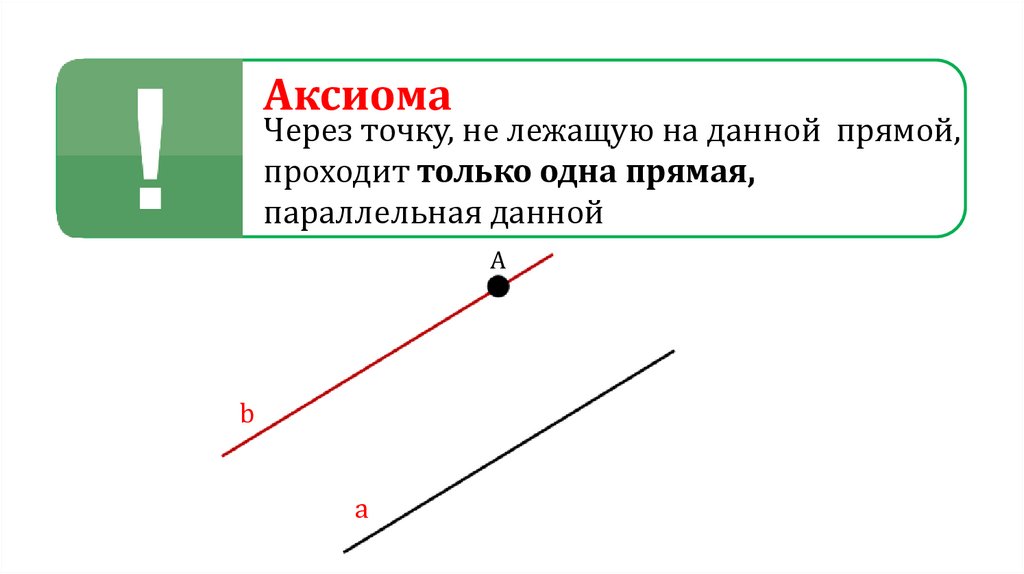
АксиомаЧерез точку, не лежащую на данной прямой,
проходит только одна прямая,
параллельная данной
А
b
a
7.
ТеоремаЧерез любую точку пространства,
не лежащую на данной прямой,
проходит прямая, параллельная
данной, и притом только одна
8.
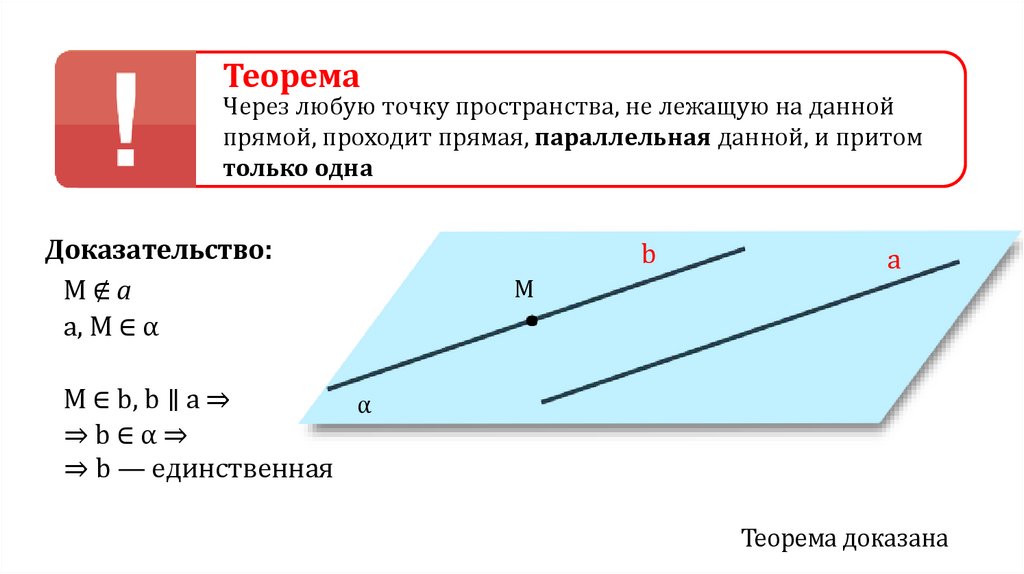
ТеоремаЧерез любую точку пространства, не лежащую на данной
прямой, проходит прямая, параллельная данной, и притом
только одна
Доказательство:
M∉a
a, M ∈ α
b
М
a
M ∈ b, b ∥ a ⇒
α
⇒b∈α⇒
⇒ b — единственная
Теорема доказана
9.
ЛеммаЕсли одна из двух параллельных
прямых пересекает данную плоскость,
то и другая прямая пересекает данную
плоскость
10.
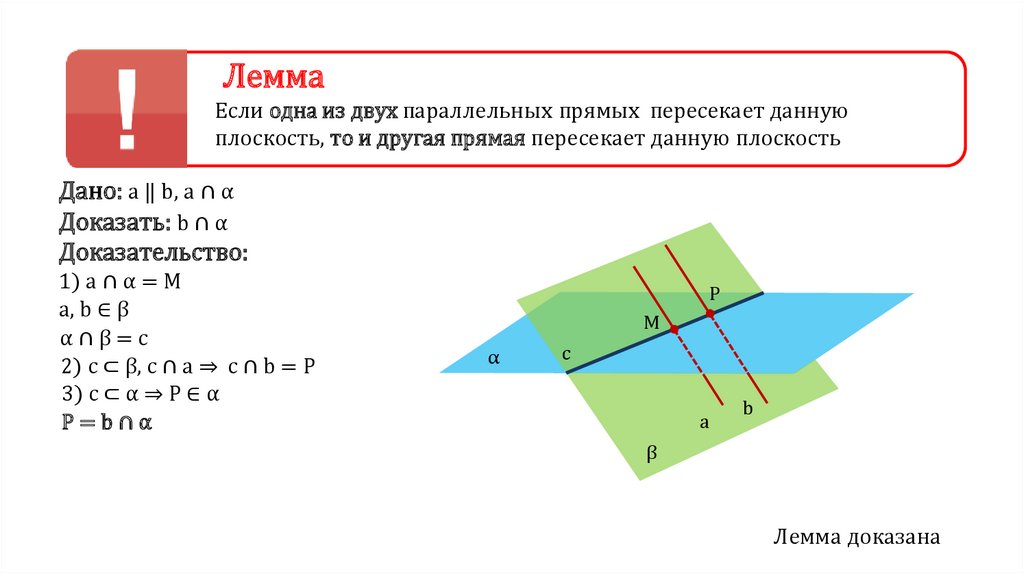
ЛеммаЕсли одна из двух параллельных прямых пересекает данную
плоскость, то и другая прямая пересекает данную плоскость
Дано: a ‖ b, a ∩ α
Доказать: b ∩ α
Доказательство:
1) a ∩ α = M
a, b ∈ β
α∩β=c
2) c ⊂ β, c ∩ a ⇒ c ∩ b = P
3) c ⊂ α ⇒ P ∈ α
P=b∩α
P
M
α
c
a
b
β
Лемма доказана
11.
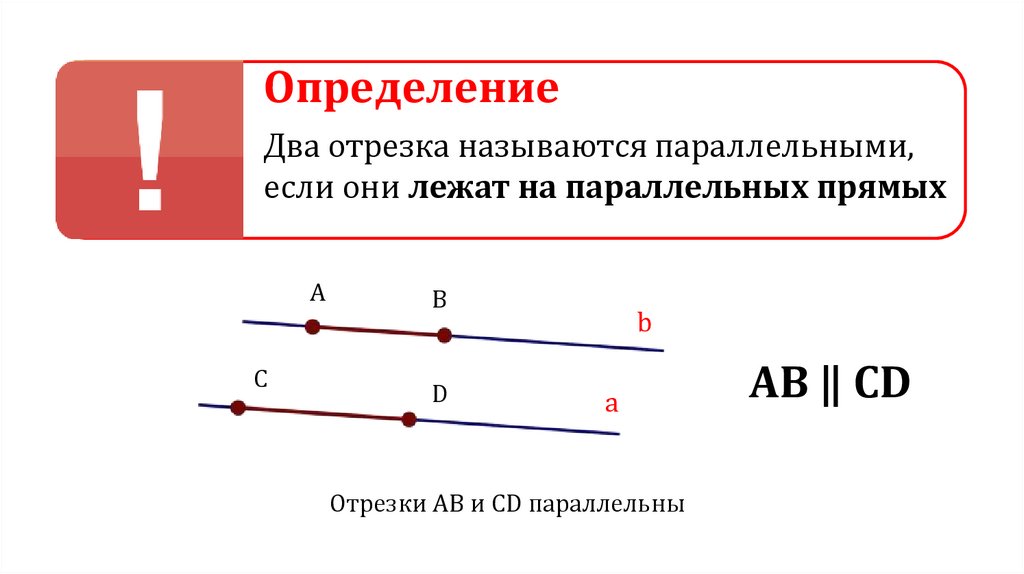
ОпределениеДва отрезка называются параллельными,
если они лежат на параллельных прямых
А
С
В
D
b
a
Отрезки AB и CD параллельны
AB ‖ CD
12.
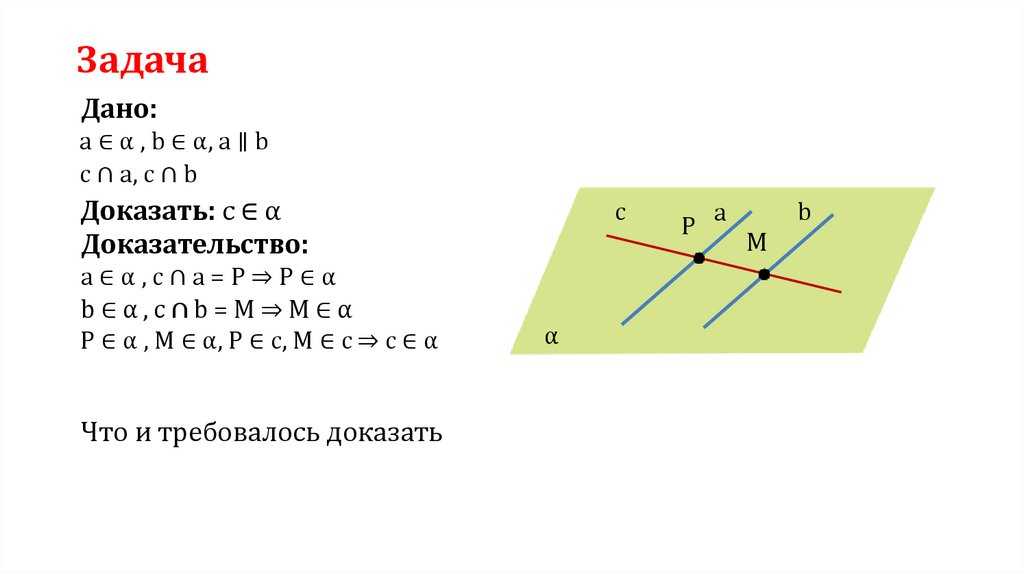
ЗадачаДано:
а ∈ α , b ∈ α, a ∥ b
c ∩ a, c ∩ b
Доказать: c ∈ α
Доказательство:
а∈α,c∩a=P⇒P∈α
b∈α,c∩b=M⇒M∈α
P ∈ α , M ∈ α, P ∈ c, M ∈ c ⇒ c ∈ α
Что и требовалось доказать
c
α
P
a
b
M



 mathematics
mathematics








